6.2反比例函数的图像和性质同步练习(含解析)
文档属性
| 名称 | 6.2反比例函数的图像和性质同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
6.2反比例函数的图像和性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.反比例函数(,)的图象位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,在平面直角坐标系中,矩形的对角线经过原点,点为轴上一点,且的面积为,双曲线经过矩形的顶点、,连接,交双曲线于点,且,若平分,则的值为( )
A. B. C. D.
3.如图所示,该函数表达式可能是( )
A. B. C. D.
4.已知点在函数的图象上,则( )
A. B. C. D.
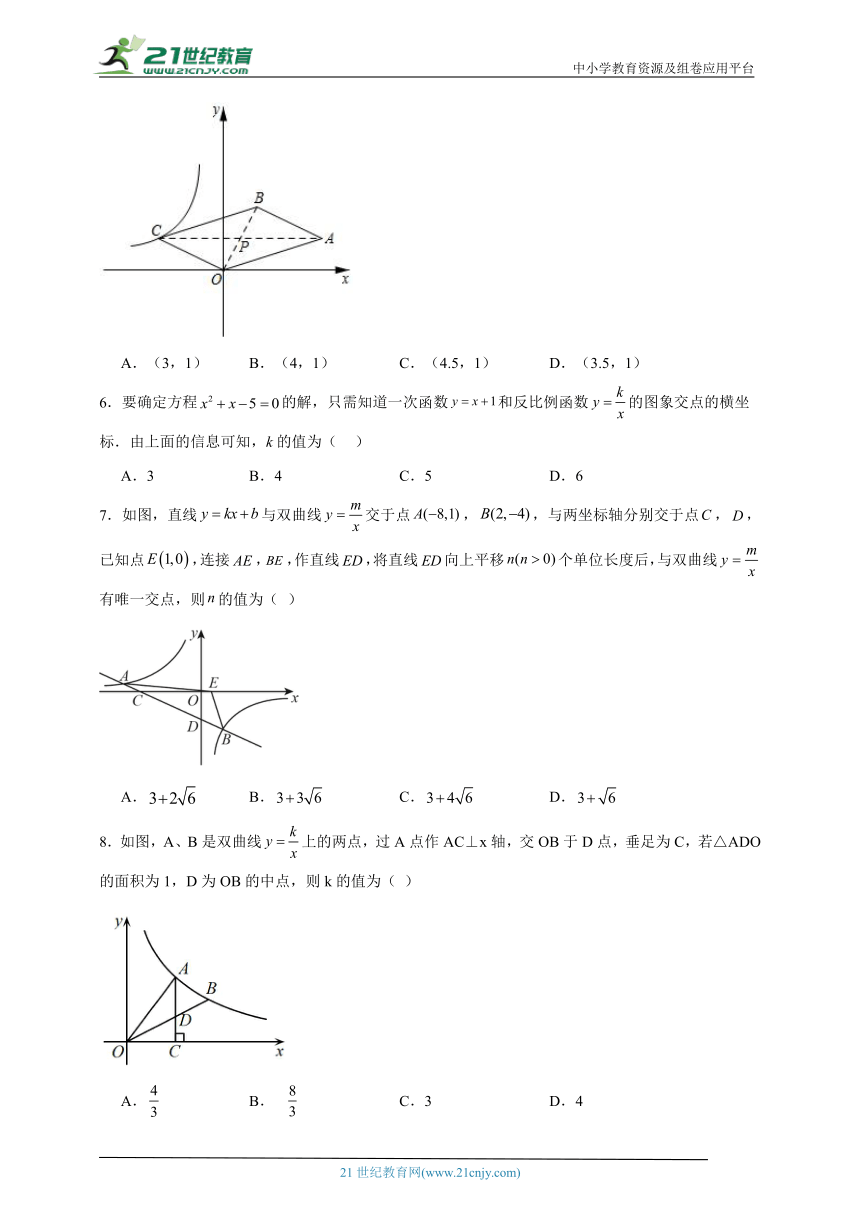
5.如图,平行四边形OABC的对角线AC、OB交于点P,点P的坐标为(,1),AC∥x轴,若函数y(x<0)的图像经过平行四边形OABC的顶点C,则点A的坐标为( )
A.(3,1) B.(4,1) C.(4.5,1) D.(3.5,1)
6.要确定方程的解,只需知道一次函数和反比例函数的图象交点的横坐标.由上面的信息可知,k的值为( )
A.3 B.4 C.5 D.6
7.如图,直线与双曲线交于点,,与两坐标轴分别交于点,,已知点,连接,,作直线,将直线向上平移个单位长度后,与双曲线有唯一交点,则的值为( )
A. B. C. D.
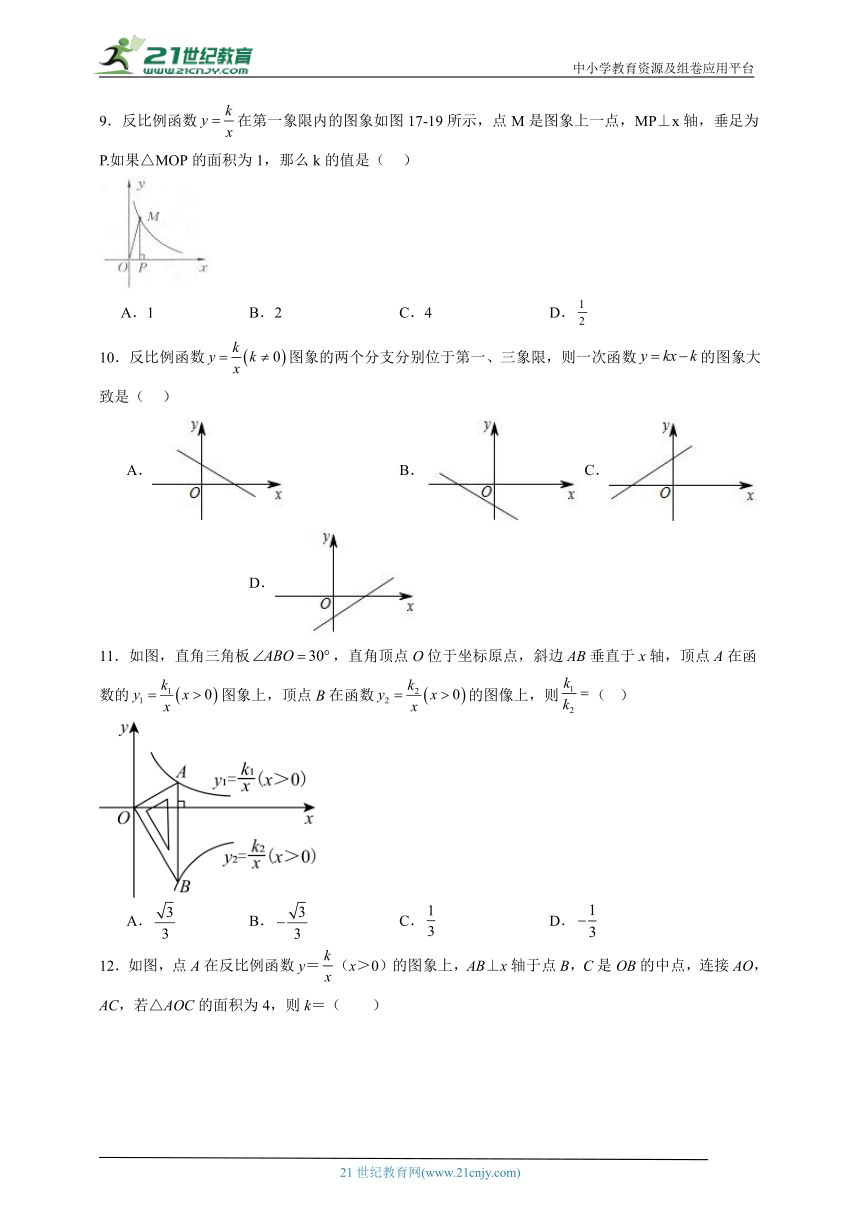
8.如图,A、B是双曲线上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为1,D为OB的中点,则k的值为( )
A. B. C.3 D.4
9.反比例函数在第一象限内的图象如图17-19所示,点M是图象上一点,MP⊥x轴,垂足为P.如果△MOP的面积为1,那么k的值是( )
A.1 B.2 C.4 D.
10.反比例函数图象的两个分支分别位于第一、三象限,则一次函数的图象大致是( )
A. B. C. D.
11.如图,直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的图象上,顶点B在函数的图像上,则( )
A. B. C. D.
12.如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
二、填空题
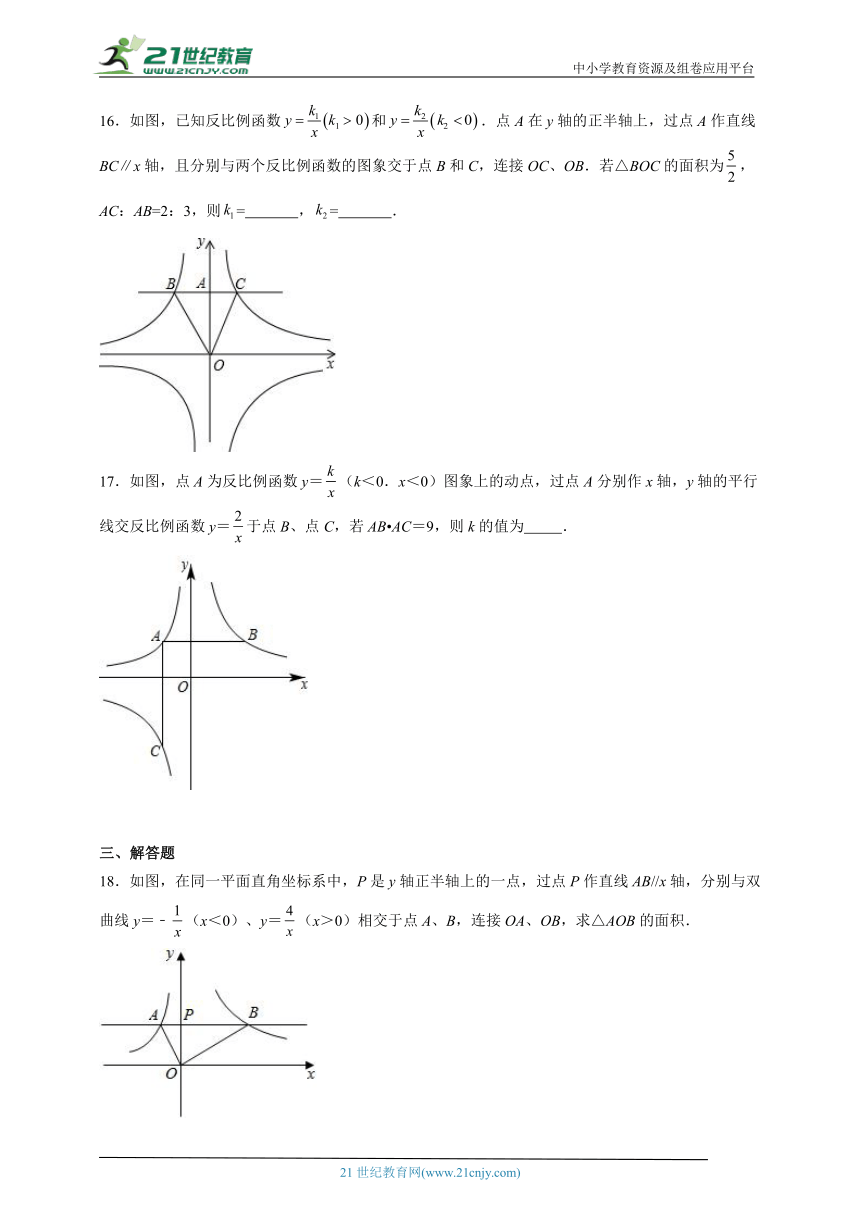
13.如图,在平面直角坐标系中,过点M(-3,2)分别作轴、轴的垂线与反比例函数的图象交于A、B两点,则四边形MAOB的面积为 .
14.如图,点,是反比例函数图像上任意两点,过点,分别作轴、轴的垂线,, .
15.如图,已知点A在反比例函数图像上,轴于点M,且的面积为4,则反比例函数的解析式为 .
16.如图,已知反比例函数和.点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为,AC:AB=2:3,则= ,= .
17.如图,点A为反比例函数y=(k<0.x<0)图象上的动点,过点A分别作x轴,y轴的平行线交反比例函数y=于点B、点C,若AB AC=9,则k的值为 .
三、解答题
18.如图,在同一平面直角坐标系中,P是y轴正半轴上的一点,过点P作直线AB//x轴,分别与双曲线y=﹣(x<0)、y=(x>0)相交于点A、B,连接OA、OB,求△AOB的面积.
19.探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数的图象,并探究该函数性质.
(1)绘制函数图象
①列表:下列是x与y的几组对应值,其中a= .
x …… ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 5 ……
y …… ﹣3.8 ﹣2.5 ﹣1 1 5 5 a ﹣1 ﹣2.5 ﹣3.8 ……
②描点:根据表中的数值描点(x,y),请补充描出点(2,a);
③连线:请用平滑的曲线顺次连接各点,画出函数图象;
(2)探究函数性质,请写出函数y=-|x|的一条性质: ;
(3)运用函数图象及性质
①写出方程-|x|=5的解 ;
②写出不等式-|x|≤1的解集 .
20.如图,反比例函数与一次函数交于两点.
(1)求一次函数的解析式,并在网格中画出一次函数的图象;
(2)根据函数图象,直接写出关于x的不等式的解集;
(3)若点A关于x轴的对称点为点D,求的面积.
21.如图,直线与双曲线交于,两点,连接,.
(1)求的面积;
(2)根据函数图象,直接写出不等式的解集是 .
22.[探究函数的图象与性质]
(1)函数的自变量x的取值范围是 ;
(2)下列四个函数图象中函数的图象大致是 ;
(3)对于函数,求当时,y的取值范围.
请将下列的求解过程补充完整.
解:∵
∴ .
∵,∴ .
[拓展运用]
(4)若函数,则y的取值范围 .
23.已知点和都在反比例函数的图象上,比较与的大小.
24.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.
《6.2反比例函数的图像和性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D A C C B B D
题号 11 12
答案 D A
1.A
【分析】本题主要考查了反比例函数的性质,根据反比例函数中k的大小决定图像的位置判断即可.
【详解】当,时,反比例函数的图像位于第一象限.
故选:A.
2.C
【分析】连接,先由平分得,由矩形的性质得到,从而得到,故而AE//BD,再由平行线的性质得到和的面积相等,然后设点的坐标,结合得到点和点的坐标,最后结合的面积求出的值.
【详解】解:连接,
∵矩形的对角线经过原点,双曲线经过矩形的顶点、,
∴点是矩形对角线与的交点,
∴,即,
∴,
∵平分
∴,
∴,
∴AE//BD,
∵的面积为,
∴,
设,
∵,
∴,,
∴,
∴.
故选:C.
【点睛】本题考查了矩形的性质,平行线的性质和判定,等腰三角形的性质,反比例函数图像上点的坐标特征,角平分线的性质等知识.解题的关键是通过平行线的判定和性质得到和的面积相等.
3.C
【分析】本题考查了反比例函数的图象.熟练掌握反比例函数的图象是解题的关键,由图象可知,反比例函数,然后对各选项进行判断作答即可.
【详解】解:由图象可知,反比例函数,
A中不是反比例函数,故不符合要求;
B中是反比例函数,但不经过第二、第四象限,故不符合要求;
C中是反比例函数,经过第二、第四象限,故符合要求;
D中不是反比例函数,故不符合要求;
故选:C.
4.D
【分析】根据反比例函数解析式可知反比例函数图象经过第二、四象限,在每个象限内y随x增大而增大,由此求解即可
【详解】解:∵反比例函数解析式为,,
∴反比例函数图象经过第二、四象限,在每个象限内y随x增大而增大,
∵点在函数的图象上,,
∴,
故选D.
【点睛】本题主要考查了比较反比例函数的函数值大小,正确根据函数解析式得到反比例函数图象经过第二、四象限,在每个象限内y随x增大而增大是解题的关键.
5.A
【分析】点C纵坐标与点P纵坐标相等,将y=1代入解析式可得点C坐标,再根据中点坐标公式求解.
【详解】解:∵AC∥x轴,点P的坐标为(,1),
∴点C纵坐标与点P纵坐标相等为1,
将y=1代入y中得:
x=﹣2,
即点C坐标为(﹣2,1),
∵平行四边形OABC的对角线AC、OB交于点P,
∴点P为AC中点,
∴,
∴,
点A坐标为(3,1).
故选:A.
【点睛】本题考查了反比例函数图象上点的坐标特征、、平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.
6.C
【分析】一次函数y=x+1和反比例函数的图象交点的横坐标是方程x+1=的解,整理后与方程x2+x-5=0比较即可求得结论.
【详解】解:∵一次函数y=x+1和反比例函数的图象交点的横坐标是方程x+1=的解,
方程x+1=整理得,x2+x-k=0,
由题意可知,k=5,
故选:C.
【点睛】本题是反比例函数与一次函数的交点问题,考查了函数与方程的关系,明确一次函数y=x+1和反比例函数的图象交点的横坐标是方程x+1=的解是解题的关键.
7.C
【分析】根据,解出直线方程解析,双曲线解析式,从而确定直线的解析式,将直线向上平移个单位长度后,可将平移后的解析式表示出来,与双曲线有唯一交点,则含有的式子的判别式为零,由此即可求解.
【详解】解:直线与双曲线交于点,,
∴,,
解得,,
∴直线方程的解析式为,双曲线的解析式为,
∴,,且,
设直线的解析式为,
∴,
解得,
∴直线的解析式为,
将直线向上平移个单位长度后的解析式为,与双曲线有唯一交点,
∴,
整理得,,
∵有唯一解,
∴根的判别式,即,且
∴,
故选:.
【点睛】本题主要考查直线方程与反比例函数的综合应用,根与系数的关系,掌握直线方程,反比例方程图像的性质,运用根的判别式判断根的情况式解题的关键.
8.B
【分析】过点B作BE⊥x轴于点E,根据D为OB的中点可知CD是△OBE的中位线, 再由△ADO的面积为1求出y的值即可得出结论.
【详解】过点B作BE⊥x轴于点E,
∵D为OB的中点,
∴CD是△OBE的中位线,即CD=BE,
设A(x,),则B(2x,),
故CD=,AD=,
∵△ADO的面积为1,
∴AD OC=1,,
解得,
∴.
故选B.
9.B
【详解】根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系S=|k|即可求得k的值.
解:由于点M是反比例函数(k>0)图象上一点,
则S△MOP=|k|=1;
又由于k>0,则k=2.
故选B.
10.D
【分析】根据题意可得,进而根据一次函数图像的性质可得的图象的大致情况.
【详解】反比例函数图象的两个分支分别位于第一、三象限,
∴一次函数的图象与y轴交于负半轴,且经过第一、三、四象限.
观察选项只有D选项符合.
故选D
【点睛】本题考查了反比例函数的性质,一次函数图像的性质,根据已知求得是解题的关键.
11.D
【分析】此题考查反比例函数的性质,30°的直角三角形的性质,设与轴的交点为,设点A的坐标为,则可得到,,根据三角形的面积得到 ,再根据和的取值范围求比值即可解题.
【详解】解:设与轴的交点为,点A的坐标为,
则,
,
,
,
∴,,
∴,
∴,
,
,
,
,
,
故选:D.
12.A
【分析】由C是OB的中点求△AOB的面积,设A(a,b)根据面积公式求ab,最后求k.
【详解】解:∵C是OB的中点,△AOC的面积为4,
∴△AOB的面积为8,
设A(a,b),
∵AB⊥x轴于点B,
∴ab=16,
∵点A在反比例函数y=(x>0)的图象上,
∴k=16.
故选A.
【点睛】本题考查了反比例函数中k的几何意义,反比例函数图象上点的坐标特征,掌握用面积法求k是解题的关键.
13.10.
【详解】试题分析:根据反比例函数的几何意义可得
所以四边形MAOB的面积为=10.
考点:反比例函数的性质、点与坐标.
14.
【分析】根据反比例函数的比例系数的几何意义得,即可求得结果.
【详解】解:∵点,是反比例函数图像上任意两点,过点,分别作轴、轴的垂线,
∴,
∵,
∴,
∴.
故答案为:.
【点睛】本题考查反比例函数中的几何意义,即图像上的点向坐标轴作垂线与坐标轴所围成的矩形面积.掌握反比例函数中的几何意义是解题的关键.
15.
【分析】根据反比例函数的比例系数k的几何意义:过反比例函数图像上一点分别做坐标轴的垂线,两垂线与坐标轴围成的矩形的面积为,据此即可得解.
【详解】解:设反比例函数的解析式为:,
反比例函数的图像在第二、四象限,
,
又轴于点M,且的面积为4,
,
,
反比例函数的解析式为:.
【点睛】此题考查了反比例函数的图像与性质,熟练掌握反比例函数中比例系数k的几何意义是解此题的关键.
16. 2 -3
【详解】解:设点A(0,a)
∵点A在y轴的正半轴上,
∴a>0,
则点B(),点C().
∴OA= a,AB=(),AC=(),
AB=.
∵△BOC的面积为,
∴,即 ①.
又∵AC:AB=2:3,
∴,即②.
联立①②,解得=2,=-3.
故答案为:
17.﹣1或﹣4.
【分析】根据反比例函数y=解析式设点A的坐标为(m,),根据点A、B、C的关系及反比例函数y=,求得B(,),C(m,),根据题意列方程即可得到结论.
【详解】解:设点A的坐标为(m,),
∵过点A分别作x轴,y轴的平行线,交反比例函数y=于点B、点C,
∴B(,),C(m,),
∴AB= m,AC= ,
∵AB AC=9,
∴( m)( )=9,
∴k= 1或k= 4,
故答案为: 1或 4.
【点睛】本题考查了反比例函数图象上点的坐标特征,根据题意列出关于k的等式是解题的关键.
18.S△AOB=.
【分析】根据反比例函数的比例系数k的几何意义求解即可.
【详解】解:∵AB⊥y轴,
∴S△OAP=,S△OBP==2,
∴S△AOB=S△OBP+S△OAP=+2=.
【点睛】本题考查反比例函数系数k的几何意义,解题的关键是理解反比例函数的比例系数k的几何意义,属于中考常考题型.
19.(1)①1;②见解析,③见解析
(2)的图象关于轴对称轴(答案不唯一)
(3)①或;②或
【分析】(1)①把x=2代入解析式即可得a的值;②③按要求描点,连线即可;
(2)观察函数图象,可得函数性质;
(3)①由函数图象可得答案;②观察函数图象即得答案.
【详解】(1)①列表:当x=2时,,
故答案为:1;
②描点,③连线如下:
(2)观察函数图象可得:的图象关于y轴对称,
故答案为:的图象关于y轴对称;
(3)①观察函数图象可得:当y=5时,x=1或x=-1,
的解是x=1或x=-1,
故答案为:x=1或x=-1,
②观察函数图象可得,当x≤-2或x≥2时,y≤1,
∴的解集是x≤-2或x≥2,
故答案为:x≤-2或x≥2.
【点睛】本题考查了列表描点画函数图象,根据函数图象获取信息,画出函数图象,从函数图象获取信息是解题的关键.
20.(1);图象见解析
(2)或
(3)6
【分析】(1)利用待定系数法求出一次函数解析式,再利用两点法画出函数图象,即可求解;
(2)由图象可知,关于x的不等式的解集为或,即可;
(3)根据点A关于x轴的对称点为点D,可得,再由三角形的面积公式,即可求解.
【详解】(1)解:∵点在反比例函数的图象上,
∴,
∴,
∴.
把A、B的坐标代入得∶
,
解得,
∴一次函数表达式为,
在网格中画出一次函数的图象如图:
(2)解:由图象可知,关于x的不等式的解集为或;
(3)解:∵,
∴,
∴,
∴.
【点睛】本题是反比例函数与一次函数的交点问题,考查反比例函数图象上点的坐标特征以及待定系数法求函数解析式,三角形的面积,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.
21.(1)的面积为8;
(2)或
【分析】(1)根据点B的坐标可以求得双曲线的解析式,然后即可求得点A的坐标,再求得直线与x轴交于点,根据的面积即可求解;
(2)根据图象即可求解.
【详解】(1)解:∵在双曲线上,
∴,
∴,
∵在双曲线上,
∴,即,
∴;
设直线与x轴交于点C,
令,则,
∴,
∴的面积;
(2)解:观察图象,不等式的解集是或;
故答案为:或.
【点睛】本题考查反比例函数与一次函数的交点问题、三角形的面积,解答本题的关键是明确题意,利用数形结合的思想解答.
22.(1)
(2)C
(3)4,4
(4)或
【分析】(1)分母上由未知数,根据分母不为零,求出取值范围即可;
(2)根据中以及反比例函数的性质,,图象过一、三象限,进行判断即可.
(3)根据配方法进行作答即可;
(4)分和两种情况,利用(3)中的方法进行配方求解即可.
【详解】(1)函数的自变量x的取值范围是;
故答案为:;
(2)∵中以及反比例函数的性质,,图象过一、三象限可得:函数的图象大致是C;
故答案为:C;
(3)解:∵
∴.
∵,
∴.
故答案为:4,4
(4)①当时,
∵,
∴.
②当时,
∵,
∴.
故答案为:或.
【点睛】本题考查了函数的图象和性质,熟记函数的性质,准确理解和掌握题目中给出的求函数值的取值范围是解题的关键.
23.当时,;当时,.
【分析】分k>0和k<0两种情况分别按照反比例函数的性质解答即可.
【详解】解:①∵当k>0时,反比例函数的函数图象的两个分支分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣2<﹣1<0,
∴点A(﹣2,),B(﹣1,)位于第三象限,且0>>.
∵3>0,∴点C(3,)位于第一象限,
∴>0,
∴;
②∵当k<0时,反比例函数的函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣2<﹣1<0,
∴点A(﹣2,),B(﹣1,)位于第二象限,且<<0.
∵3>0,
∴点C(3,)位于第四象限,
∴<0,
∴.
【点睛】本题主要考查了反比例函数图象上点的坐标特征,掌握分类讨论思想成为解答本题的关键.
24.(1)k=10,b=3;(2).
【详解】试题分析:(1)、将A点坐标代入反比例函数解析式和一次函数解析式分别求出k和b的值;(2)、首先根据一次函数求出点B的坐标,然后计算面积.
试题解析:(1)、把x=2,y=5代入y=,得k==2×5=10
把x=2,y=5代入y=x+b,得b=3
(2)、∵y=x+3 ∴当y=0时,x=-3, ∴OB=3 ∴S=×3×5=7.5
考点:一次函数与反比例函数的综合问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.2反比例函数的图像和性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.反比例函数(,)的图象位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,在平面直角坐标系中,矩形的对角线经过原点,点为轴上一点,且的面积为,双曲线经过矩形的顶点、,连接,交双曲线于点,且,若平分,则的值为( )
A. B. C. D.
3.如图所示,该函数表达式可能是( )
A. B. C. D.
4.已知点在函数的图象上,则( )
A. B. C. D.
5.如图,平行四边形OABC的对角线AC、OB交于点P,点P的坐标为(,1),AC∥x轴,若函数y(x<0)的图像经过平行四边形OABC的顶点C,则点A的坐标为( )
A.(3,1) B.(4,1) C.(4.5,1) D.(3.5,1)
6.要确定方程的解,只需知道一次函数和反比例函数的图象交点的横坐标.由上面的信息可知,k的值为( )
A.3 B.4 C.5 D.6
7.如图,直线与双曲线交于点,,与两坐标轴分别交于点,,已知点,连接,,作直线,将直线向上平移个单位长度后,与双曲线有唯一交点,则的值为( )
A. B. C. D.
8.如图,A、B是双曲线上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为1,D为OB的中点,则k的值为( )
A. B. C.3 D.4
9.反比例函数在第一象限内的图象如图17-19所示,点M是图象上一点,MP⊥x轴,垂足为P.如果△MOP的面积为1,那么k的值是( )
A.1 B.2 C.4 D.
10.反比例函数图象的两个分支分别位于第一、三象限,则一次函数的图象大致是( )
A. B. C. D.
11.如图,直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的图象上,顶点B在函数的图像上,则( )
A. B. C. D.
12.如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
二、填空题
13.如图,在平面直角坐标系中,过点M(-3,2)分别作轴、轴的垂线与反比例函数的图象交于A、B两点,则四边形MAOB的面积为 .
14.如图,点,是反比例函数图像上任意两点,过点,分别作轴、轴的垂线,, .
15.如图,已知点A在反比例函数图像上,轴于点M,且的面积为4,则反比例函数的解析式为 .
16.如图,已知反比例函数和.点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为,AC:AB=2:3,则= ,= .
17.如图,点A为反比例函数y=(k<0.x<0)图象上的动点,过点A分别作x轴,y轴的平行线交反比例函数y=于点B、点C,若AB AC=9,则k的值为 .
三、解答题
18.如图,在同一平面直角坐标系中,P是y轴正半轴上的一点,过点P作直线AB//x轴,分别与双曲线y=﹣(x<0)、y=(x>0)相交于点A、B,连接OA、OB,求△AOB的面积.
19.探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数的图象,并探究该函数性质.
(1)绘制函数图象
①列表:下列是x与y的几组对应值,其中a= .
x …… ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 5 ……
y …… ﹣3.8 ﹣2.5 ﹣1 1 5 5 a ﹣1 ﹣2.5 ﹣3.8 ……
②描点:根据表中的数值描点(x,y),请补充描出点(2,a);
③连线:请用平滑的曲线顺次连接各点,画出函数图象;
(2)探究函数性质,请写出函数y=-|x|的一条性质: ;
(3)运用函数图象及性质
①写出方程-|x|=5的解 ;
②写出不等式-|x|≤1的解集 .
20.如图,反比例函数与一次函数交于两点.
(1)求一次函数的解析式,并在网格中画出一次函数的图象;
(2)根据函数图象,直接写出关于x的不等式的解集;
(3)若点A关于x轴的对称点为点D,求的面积.
21.如图,直线与双曲线交于,两点,连接,.
(1)求的面积;
(2)根据函数图象,直接写出不等式的解集是 .
22.[探究函数的图象与性质]
(1)函数的自变量x的取值范围是 ;
(2)下列四个函数图象中函数的图象大致是 ;
(3)对于函数,求当时,y的取值范围.
请将下列的求解过程补充完整.
解:∵
∴ .
∵,∴ .
[拓展运用]
(4)若函数,则y的取值范围 .
23.已知点和都在反比例函数的图象上,比较与的大小.
24.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.
《6.2反比例函数的图像和性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D A C C B B D
题号 11 12
答案 D A
1.A
【分析】本题主要考查了反比例函数的性质,根据反比例函数中k的大小决定图像的位置判断即可.
【详解】当,时,反比例函数的图像位于第一象限.
故选:A.
2.C
【分析】连接,先由平分得,由矩形的性质得到,从而得到,故而AE//BD,再由平行线的性质得到和的面积相等,然后设点的坐标,结合得到点和点的坐标,最后结合的面积求出的值.
【详解】解:连接,
∵矩形的对角线经过原点,双曲线经过矩形的顶点、,
∴点是矩形对角线与的交点,
∴,即,
∴,
∵平分
∴,
∴,
∴AE//BD,
∵的面积为,
∴,
设,
∵,
∴,,
∴,
∴.
故选:C.
【点睛】本题考查了矩形的性质,平行线的性质和判定,等腰三角形的性质,反比例函数图像上点的坐标特征,角平分线的性质等知识.解题的关键是通过平行线的判定和性质得到和的面积相等.
3.C
【分析】本题考查了反比例函数的图象.熟练掌握反比例函数的图象是解题的关键,由图象可知,反比例函数,然后对各选项进行判断作答即可.
【详解】解:由图象可知,反比例函数,
A中不是反比例函数,故不符合要求;
B中是反比例函数,但不经过第二、第四象限,故不符合要求;
C中是反比例函数,经过第二、第四象限,故符合要求;
D中不是反比例函数,故不符合要求;
故选:C.
4.D
【分析】根据反比例函数解析式可知反比例函数图象经过第二、四象限,在每个象限内y随x增大而增大,由此求解即可
【详解】解:∵反比例函数解析式为,,
∴反比例函数图象经过第二、四象限,在每个象限内y随x增大而增大,
∵点在函数的图象上,,
∴,
故选D.
【点睛】本题主要考查了比较反比例函数的函数值大小,正确根据函数解析式得到反比例函数图象经过第二、四象限,在每个象限内y随x增大而增大是解题的关键.
5.A
【分析】点C纵坐标与点P纵坐标相等,将y=1代入解析式可得点C坐标,再根据中点坐标公式求解.
【详解】解:∵AC∥x轴,点P的坐标为(,1),
∴点C纵坐标与点P纵坐标相等为1,
将y=1代入y中得:
x=﹣2,
即点C坐标为(﹣2,1),
∵平行四边形OABC的对角线AC、OB交于点P,
∴点P为AC中点,
∴,
∴,
点A坐标为(3,1).
故选:A.
【点睛】本题考查了反比例函数图象上点的坐标特征、、平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.
6.C
【分析】一次函数y=x+1和反比例函数的图象交点的横坐标是方程x+1=的解,整理后与方程x2+x-5=0比较即可求得结论.
【详解】解:∵一次函数y=x+1和反比例函数的图象交点的横坐标是方程x+1=的解,
方程x+1=整理得,x2+x-k=0,
由题意可知,k=5,
故选:C.
【点睛】本题是反比例函数与一次函数的交点问题,考查了函数与方程的关系,明确一次函数y=x+1和反比例函数的图象交点的横坐标是方程x+1=的解是解题的关键.
7.C
【分析】根据,解出直线方程解析,双曲线解析式,从而确定直线的解析式,将直线向上平移个单位长度后,可将平移后的解析式表示出来,与双曲线有唯一交点,则含有的式子的判别式为零,由此即可求解.
【详解】解:直线与双曲线交于点,,
∴,,
解得,,
∴直线方程的解析式为,双曲线的解析式为,
∴,,且,
设直线的解析式为,
∴,
解得,
∴直线的解析式为,
将直线向上平移个单位长度后的解析式为,与双曲线有唯一交点,
∴,
整理得,,
∵有唯一解,
∴根的判别式,即,且
∴,
故选:.
【点睛】本题主要考查直线方程与反比例函数的综合应用,根与系数的关系,掌握直线方程,反比例方程图像的性质,运用根的判别式判断根的情况式解题的关键.
8.B
【分析】过点B作BE⊥x轴于点E,根据D为OB的中点可知CD是△OBE的中位线, 再由△ADO的面积为1求出y的值即可得出结论.
【详解】过点B作BE⊥x轴于点E,
∵D为OB的中点,
∴CD是△OBE的中位线,即CD=BE,
设A(x,),则B(2x,),
故CD=,AD=,
∵△ADO的面积为1,
∴AD OC=1,,
解得,
∴.
故选B.
9.B
【详解】根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系S=|k|即可求得k的值.
解:由于点M是反比例函数(k>0)图象上一点,
则S△MOP=|k|=1;
又由于k>0,则k=2.
故选B.
10.D
【分析】根据题意可得,进而根据一次函数图像的性质可得的图象的大致情况.
【详解】反比例函数图象的两个分支分别位于第一、三象限,
∴一次函数的图象与y轴交于负半轴,且经过第一、三、四象限.
观察选项只有D选项符合.
故选D
【点睛】本题考查了反比例函数的性质,一次函数图像的性质,根据已知求得是解题的关键.
11.D
【分析】此题考查反比例函数的性质,30°的直角三角形的性质,设与轴的交点为,设点A的坐标为,则可得到,,根据三角形的面积得到 ,再根据和的取值范围求比值即可解题.
【详解】解:设与轴的交点为,点A的坐标为,
则,
,
,
,
∴,,
∴,
∴,
,
,
,
,
,
故选:D.
12.A
【分析】由C是OB的中点求△AOB的面积,设A(a,b)根据面积公式求ab,最后求k.
【详解】解:∵C是OB的中点,△AOC的面积为4,
∴△AOB的面积为8,
设A(a,b),
∵AB⊥x轴于点B,
∴ab=16,
∵点A在反比例函数y=(x>0)的图象上,
∴k=16.
故选A.
【点睛】本题考查了反比例函数中k的几何意义,反比例函数图象上点的坐标特征,掌握用面积法求k是解题的关键.
13.10.
【详解】试题分析:根据反比例函数的几何意义可得
所以四边形MAOB的面积为=10.
考点:反比例函数的性质、点与坐标.
14.
【分析】根据反比例函数的比例系数的几何意义得,即可求得结果.
【详解】解:∵点,是反比例函数图像上任意两点,过点,分别作轴、轴的垂线,
∴,
∵,
∴,
∴.
故答案为:.
【点睛】本题考查反比例函数中的几何意义,即图像上的点向坐标轴作垂线与坐标轴所围成的矩形面积.掌握反比例函数中的几何意义是解题的关键.
15.
【分析】根据反比例函数的比例系数k的几何意义:过反比例函数图像上一点分别做坐标轴的垂线,两垂线与坐标轴围成的矩形的面积为,据此即可得解.
【详解】解:设反比例函数的解析式为:,
反比例函数的图像在第二、四象限,
,
又轴于点M,且的面积为4,
,
,
反比例函数的解析式为:.
【点睛】此题考查了反比例函数的图像与性质,熟练掌握反比例函数中比例系数k的几何意义是解此题的关键.
16. 2 -3
【详解】解:设点A(0,a)
∵点A在y轴的正半轴上,
∴a>0,
则点B(),点C().
∴OA= a,AB=(),AC=(),
AB=.
∵△BOC的面积为,
∴,即 ①.
又∵AC:AB=2:3,
∴,即②.
联立①②,解得=2,=-3.
故答案为:
17.﹣1或﹣4.
【分析】根据反比例函数y=解析式设点A的坐标为(m,),根据点A、B、C的关系及反比例函数y=,求得B(,),C(m,),根据题意列方程即可得到结论.
【详解】解:设点A的坐标为(m,),
∵过点A分别作x轴,y轴的平行线,交反比例函数y=于点B、点C,
∴B(,),C(m,),
∴AB= m,AC= ,
∵AB AC=9,
∴( m)( )=9,
∴k= 1或k= 4,
故答案为: 1或 4.
【点睛】本题考查了反比例函数图象上点的坐标特征,根据题意列出关于k的等式是解题的关键.
18.S△AOB=.
【分析】根据反比例函数的比例系数k的几何意义求解即可.
【详解】解:∵AB⊥y轴,
∴S△OAP=,S△OBP==2,
∴S△AOB=S△OBP+S△OAP=+2=.
【点睛】本题考查反比例函数系数k的几何意义,解题的关键是理解反比例函数的比例系数k的几何意义,属于中考常考题型.
19.(1)①1;②见解析,③见解析
(2)的图象关于轴对称轴(答案不唯一)
(3)①或;②或
【分析】(1)①把x=2代入解析式即可得a的值;②③按要求描点,连线即可;
(2)观察函数图象,可得函数性质;
(3)①由函数图象可得答案;②观察函数图象即得答案.
【详解】(1)①列表:当x=2时,,
故答案为:1;
②描点,③连线如下:
(2)观察函数图象可得:的图象关于y轴对称,
故答案为:的图象关于y轴对称;
(3)①观察函数图象可得:当y=5时,x=1或x=-1,
的解是x=1或x=-1,
故答案为:x=1或x=-1,
②观察函数图象可得,当x≤-2或x≥2时,y≤1,
∴的解集是x≤-2或x≥2,
故答案为:x≤-2或x≥2.
【点睛】本题考查了列表描点画函数图象,根据函数图象获取信息,画出函数图象,从函数图象获取信息是解题的关键.
20.(1);图象见解析
(2)或
(3)6
【分析】(1)利用待定系数法求出一次函数解析式,再利用两点法画出函数图象,即可求解;
(2)由图象可知,关于x的不等式的解集为或,即可;
(3)根据点A关于x轴的对称点为点D,可得,再由三角形的面积公式,即可求解.
【详解】(1)解:∵点在反比例函数的图象上,
∴,
∴,
∴.
把A、B的坐标代入得∶
,
解得,
∴一次函数表达式为,
在网格中画出一次函数的图象如图:
(2)解:由图象可知,关于x的不等式的解集为或;
(3)解:∵,
∴,
∴,
∴.
【点睛】本题是反比例函数与一次函数的交点问题,考查反比例函数图象上点的坐标特征以及待定系数法求函数解析式,三角形的面积,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.
21.(1)的面积为8;
(2)或
【分析】(1)根据点B的坐标可以求得双曲线的解析式,然后即可求得点A的坐标,再求得直线与x轴交于点,根据的面积即可求解;
(2)根据图象即可求解.
【详解】(1)解:∵在双曲线上,
∴,
∴,
∵在双曲线上,
∴,即,
∴;
设直线与x轴交于点C,
令,则,
∴,
∴的面积;
(2)解:观察图象,不等式的解集是或;
故答案为:或.
【点睛】本题考查反比例函数与一次函数的交点问题、三角形的面积,解答本题的关键是明确题意,利用数形结合的思想解答.
22.(1)
(2)C
(3)4,4
(4)或
【分析】(1)分母上由未知数,根据分母不为零,求出取值范围即可;
(2)根据中以及反比例函数的性质,,图象过一、三象限,进行判断即可.
(3)根据配方法进行作答即可;
(4)分和两种情况,利用(3)中的方法进行配方求解即可.
【详解】(1)函数的自变量x的取值范围是;
故答案为:;
(2)∵中以及反比例函数的性质,,图象过一、三象限可得:函数的图象大致是C;
故答案为:C;
(3)解:∵
∴.
∵,
∴.
故答案为:4,4
(4)①当时,
∵,
∴.
②当时,
∵,
∴.
故答案为:或.
【点睛】本题考查了函数的图象和性质,熟记函数的性质,准确理解和掌握题目中给出的求函数值的取值范围是解题的关键.
23.当时,;当时,.
【分析】分k>0和k<0两种情况分别按照反比例函数的性质解答即可.
【详解】解:①∵当k>0时,反比例函数的函数图象的两个分支分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣2<﹣1<0,
∴点A(﹣2,),B(﹣1,)位于第三象限,且0>>.
∵3>0,∴点C(3,)位于第一象限,
∴>0,
∴;
②∵当k<0时,反比例函数的函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣2<﹣1<0,
∴点A(﹣2,),B(﹣1,)位于第二象限,且<<0.
∵3>0,
∴点C(3,)位于第四象限,
∴<0,
∴.
【点睛】本题主要考查了反比例函数图象上点的坐标特征,掌握分类讨论思想成为解答本题的关键.
24.(1)k=10,b=3;(2).
【详解】试题分析:(1)、将A点坐标代入反比例函数解析式和一次函数解析式分别求出k和b的值;(2)、首先根据一次函数求出点B的坐标,然后计算面积.
试题解析:(1)、把x=2,y=5代入y=,得k==2×5=10
把x=2,y=5代入y=x+b,得b=3
(2)、∵y=x+3 ∴当y=0时,x=-3, ∴OB=3 ∴S=×3×5=7.5
考点:一次函数与反比例函数的综合问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
