4.2平行四边形及其性质同步练习(含解析)
文档属性
| 名称 | 4.2平行四边形及其性质同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 14:30:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
4.2平行四边形及其性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,,平分,交边于点E,则线段的长度分别是( )
A.2和3 B.3和2 C.4和1 D.1和4
2.如图所示,在中,的平分线交于点,若,,则的周长是( )
A.10 B.12 C.9 D.15
3.如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
A.100° B.95° C.90° D.85°
4.如图,在中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于( )
A.2 B.3 C.4 D.5
5.平行四边形的一组对角的平分线( )
A.一定相互平行 B.一定相交 C.可能平行也可能相交 D.平行或共线
6.如图,在中,E,F是对角线上的两点,则添加①;②;③;④中任意一个条件,能够使的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在 ABCD中,下列说法一定正确的是( )
A.AC=BD B.AC⊥BD C.AB=CD D.AB=BC
8.中,,则的度数是( )
A.20° B.30° C.40° D.150°
9.如图,平行四边形的对角线交于点,平分交于点,且,,连接.下列结论:①;②;③;④.其中成立的个数有( )
A.个 B.个 C.个 D.个
10.如图,在平行四边形ABCD中,∠BAD的平分线交CD于点G,AD=AE.若AD=5,DE=6,则AG的长是( )
A.6 B.8 C.10 D.12
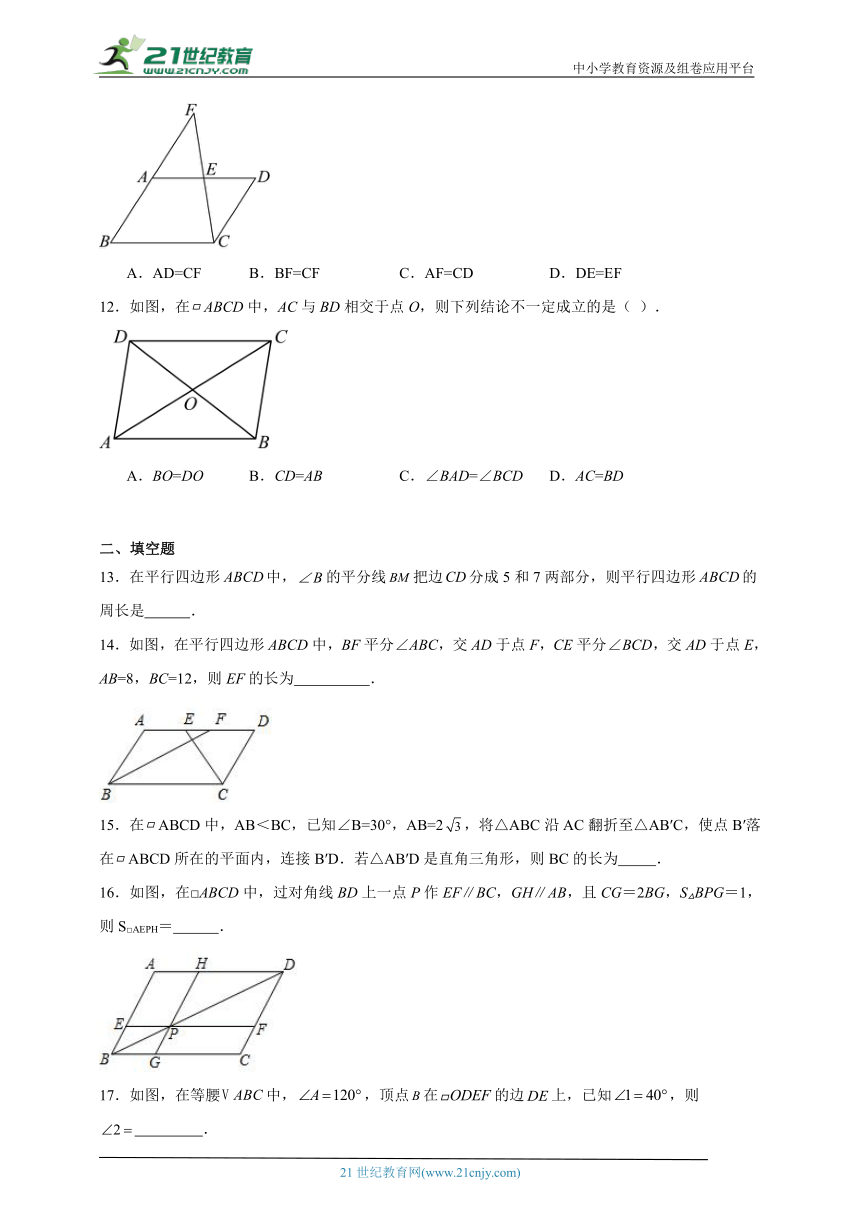
11.如图,E是 ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是( )
A.AD=CF B.BF=CF C.AF=CD D.DE=EF
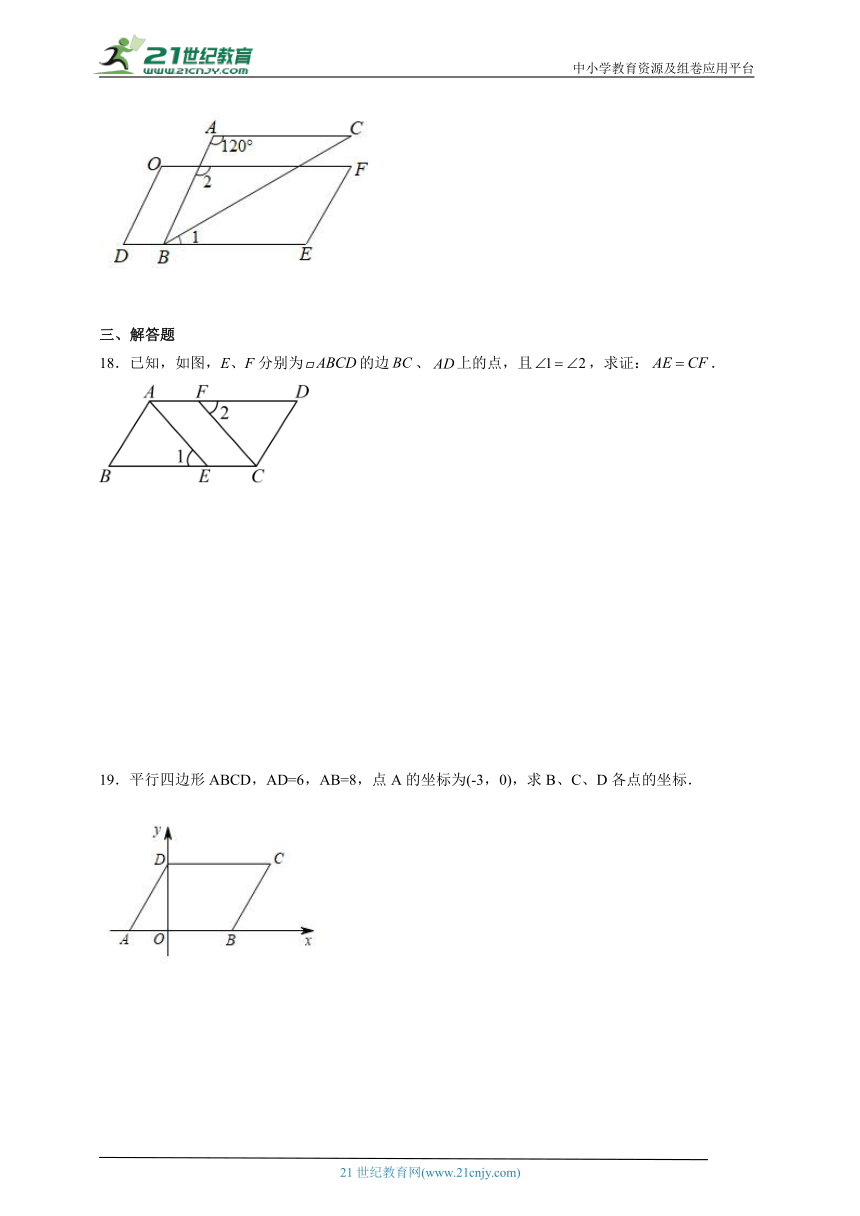
12.如图,在ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( ).
A.BO=DO B.CD=AB C.∠BAD=∠BCD D.AC=BD
二、填空题
13.在平行四边形中,的平分线把边分成5和7两部分,则平行四边形的周长是 .
14.如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=8,BC=12,则EF的长为 .
15.在ABCD中,AB<BC,已知∠B=30°,AB=2,将△ABC沿AC翻折至△AB′C,使点B′落在ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 .
16.如图,在□ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S□AEPH= .
17.如图,在等腰中,,顶点在的边上,已知,则 .
三、解答题
18.已知,如图,E、F分别为的边、上的点,且,求证:.
19.平行四边形ABCD,AD=6,AB=8,点A的坐标为(-3,0),求B、C、D各点的坐标.
20.已知:如图,在中,的平分线交于点,的平分线交于点,交于点.
求证:.
21.如图,在平行四边形中,的平分线与的延长线相交于点E,于点H.
(1)求证:;
(2)若,求的长.
22.问题探究:已知平行四边形的面积为,是所在直线上一点.
如图:当点与重合时,________;
如图,当点与与均不重合时,________;
如图,当点在(或)的延长线时,________.
拓展推广:如图,平行四边形的面积为,、分别为、延长线上两点,连接、、、,求出图中阴影部分的面积,并说明理由.
实践应用:如图是一平行四边形绿地,、分别平行于、,它们相交于点,,,,,现进行绿地改造,在绿地内部作一个三角形区域(连接、、,图中阴影部分)种植不同的花草,求出三角形区域的面积.
23.已知:如图,在□ABCD中,从顶点D向AB作垂线,垂足为E,且E是AB的中点,若□ABCD的周长为8.6cm,△ABD的周长为6cm,求AB、BC的长.
24.已知:如图,在平行四边形中,的平分线交于点,过点作的垂线交于点,交延长线于点,连接,.
(1)求证:;
(2)若,,, 求的长.
《4.2平行四边形及其性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C B D C C B B B
题号 11 12
答案 B D
1.B
【分析】本题主要考查了角平分线、平行四边形的性质及等腰三角形的判定,根据已知得出∠BAE=∠AEB是解决问题的关键.
先根据角平分线及平行线的性质得出,再由等角对等边得出,从而求出的长.
【详解】解:∵四边形是平行四边形,
∴,,
∴,
∵平分,,
∴,
∴,
∴,
∴,
故选:B.
2.A
【分析】在平行四边形ABCD中,根据对边平行且相等可得: ,又由BE是的平分线,可得,
易得AE=AB,即可求得的周长.
【详解】∵四边形ABCD是平行四边形
∴
∴
∵BE是的平分线
∴
∴
∴AE=AB=2
∵
∴
∴
∴的周长为10
故选:A
【点睛】本题考查的知识点主要是平行四边形的性质,解题中结合等腰三角形的判定“等边对等角”是关键.
3.C
【详解】在中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
4.B
【分析】由四边形ABCD为平行四边形,得到AD与BC平行,AD=BC,利用两直线平行得到一对内错角相等,由BE为角平分线得到一对角相等,等量代换得到∠ABE=∠AEB,利用等角对等边得到AB=AE=4,由AD﹣AE求出ED的长即可.
【详解】解:∵四边形ABCD为平行四边形,
∴AD//BC,AD=BC=7,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE=4,
∴ED=AD﹣AE=BC﹣AE=7﹣4=3.
故选:B.
【点睛】此题考查了角平分线的定义,等腰三角形的判定,以及平行四边形的性质,熟练掌握平行四边形的性质是解本题的关键.
5.D
【分析】分两种情况:如果平行四边形的邻边不相等,那么它的一组对角的平分线互相平行;如果平行四边形的邻边相等,那么它的一组对角的平分线共线.
【详解】解:如图,中,AE、CF分别平分∠BAD、∠BCD,
∵四边形ABCD是平行四边形,AD∥BC,
∴∠BAD=∠BCD,∠2=∠3,
∵AE、CF分别平分∠BAD、∠BCD,
∴,
∴∠2=∠4,
∴∠3=∠4,
∴AE∥CF;
当是菱形时,AE与CF共线.
故选:D.
【点睛】本题主要考查了平行四边形的性质,角平分线的定义,平行线的判定,将平行四边形分类讨论是解决本题的关键.
6.C
【分析】本题考查了全等三角形的判定定理,熟练掌握全等三角形的判定定理是解题的关键;根据全等三角形的判定定理,逐项判断即可.
【详解】∵四边形是平行四边形,
∴,
∴,
当时,由可证,所以①符合题意;
当时,可得,即,由可证,所以②符合题意;
当时,不能判定,所以③不符合题意;
当时,由可证,所以④符合题意.
∴满足题意的有3个.
故选:C.
7.C
【详解】解:∵平行四边形的两组对边分别平行且相等,对角线互相平分,
∴C正确,其余不一定正确,
故选C.
8.B
【分析】本题考查平行四边形的性质,掌握平行四边形邻角互补对角相等是解题的关键,根据平行四边形的性质可知,,结合可求出,从而得解.
【详解】在中,,,
又∵,
∴,
∴,
故选:B.
9.B
【分析】此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质,证得是等边三角形以及是的中位线是解答本题的关键.
由中,,易得是等边三角形,又由,证得;继而证得,得;由、以及,可得;可得是三角形的中位线,证得.
【详解】解:四边形是平行四边形,
,,
平分,
,
是等边三角形,
,
,
,
,
,故正确;
,
,故正确;
,,
,
,故错误;
,,,
,
,
,
,
,故错误;
故选:B.
10.B
【分析】由等腰三角形的角平分线性质得到DH=EH=3,由平行四边形的性质和平行线的性质得到DA=DG,AH=GH,再由勾股定理AH=,从而得到正确答案.
【详解】如图,设AG交BD于H.
∵AD=AE,AG平分∠BAD,
∴AG垂直平分DE,
∴DH=EH=3,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠AGD=∠GAB,
∵∠DAG=∠GAB,
∴∠DAG=∠DGA,
∴DA=DG,
∵DE⊥AG,
∴AH=GH,
在Rt△ADH中,AH===4,
∴AG=2AH=8.
故选B.
【点睛】本题考查了平行四边形的性质、等腰三角形的角平分线性质、勾股定理和平行线的性质,解题的关键是推得DA=DG 和AH=GH.
11.B
【详解】∵ABCD是平行四边形,∴AD=BC,∠B=∠D,AB∥CD.∵BF∥CD,∴∠F=∠FCD,∠FAE=∠D.∵AE=ED,∴△AEF≌△DEC.∴AF=CD,EF=CE.∵∠FCD=∠D,∴CE=DE.∴DE=EF.故C、D都成立;∵∠B=∠D=∠F,则CF=BC=AD.故A成立.没有条件证明BF=CF.
12.D
【分析】根据平行四边形的性质判断即可
【详解】解:A、∵四边形ABCD是平行四边形,
∴OB=OD(平行四边形的对角线互相平分),正确,不符合题意;
B、∵四边形ABCD是平行四边形,
∴CD=AB(平行四边形的对边相等),正确,不符合题意;
C、∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD(平行四边形的对角相等),正确,不符合题意;
D、根据四边形ABCD是平行四边形不能推出AC=BD,错误,符合题意.
故选D.
13.34或38
【分析】本题主要考查了平行四边形的性质,等腰三角形的判定,三角形的角平分线等知识点,解此题的关键是求出.分类讨论.
由平行四边形推出,由已知得到,推出,分两种情况(1)当时,;(2)当时,求.
【详解】解:∵平行四边形中,的平分线把边分成5和7两部分,
∴,
∵,
∴,
∴,
∴,
∴当时,平行四边形的周长是,
当时,平行四边形的周长是,
∴平行四边形的周长是34或38.
故答案为:34或38.
14.4
【分析】根据平行四边形的性质可得,由角平分线可得,所以,所以,同理可得,则根据即可求解.
【详解】∵四边形是平行四边形,
∴,,,
∴,
∴平分,
∴,
∴,
∴,
同理可得,
∴.
故答案为:4
【点睛】本题主要考查了平行四边形的性质、角平分线的定义,转化线段是解题的关键.
15.4或6.
【详解】试题分析:本题主要考查了翻折变换的性质,解题的关键是画出图形,发现存在两种情况,进行分类讨论.在ABCD中,AB<BC,要使△AB′D是直角三角形,有两种情况:∠B′AD=90°或∠AB′D=90°,画出图形,分类讨论:(1)当∠B′AD=90°AB<BC时,如图1,延长B′A交BC于点G,利用平行四边形和直角三角形的性质,可求出BC的长为6;(2)当∠AB′D=90°时,如图2,由平行四边形的性质可求出四边形ACDB′是等腰梯形,然后根据∠AB′D=90°,得出四边形ACDB′是矩形,再通过解直角三角形,得出BC的长为4.
解:当∠B′AD=90°AB<BC时,如图1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2,
∴∠AB′C=30°,
∴GC=B′C=BC,
∴G是BC的中点,
在RT△ABG中,BG=AB=×2=3,
∴BC=6;
当∠AB′D=90°时,如图2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2,
∴BC=AB÷=2×=4,
∴当BC的长为4或6时,△AB′D是直角三角形.
故答案为4或6.
考点:1.翻折变换(折叠问题);2.平行四边形的性质;3.等腰梯形、矩形和直角三角形.
16.4
【分析】由条件可证明四边形HPFD、BEPG为平行四边形,可证明S四边形AEPH=S四边形PFCG.,再利用面积的和差可得出四边形AEPH和四边形PFCG的面积相等,由已知条件即可得出答案.
【详解】解:∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG、AEPH、CFPG为平行四边形,
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD-S△PEB-S△PHD=S△CDB-S△BGP-S△DFP,
即S四边形AEPH=S四边形PFCG.
∵CG=2BG,S△BPG=1,
∴S四边形AEPH=S四边形PFCG=4×1=4;
故答案为:4.
【点睛】本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行 四边形为平行四边形,②两组对边分别相等 四边形为平行四边形,③一组对边平行且相等 四边形为平行四边形,④两组对角分别相等 四边形为平行四边形,⑤对角线互相平分 四边形为平行四边形.
17.110
【分析】先根据等腰三角形的性质求出∠ABC的度数;再根据平行四边形对边平行和两直线平行同旁内角互补的性质,得出∠2+∠ABE=180 ,代入求解即可.
【详解】解:∵是等腰三角形,∠A=120 ,
∴∠ABC=∠C=(180 -∠A)÷2=30 ,
∵四边形是平行四边形,
∴OFDE,
∴∠2+∠ABE=180 ,
即∠2+30 +40 =180 ,
∴∠2=110 .
故答案为:110 .
【点睛】此题考查了等腰三角形的性质和平行四边形的性质,解题的关键是数形结合,熟练运用上述知识求解.
18.见详解
【分析】根据条件证明,即可得出结论.
【详解】证明:∵四边形是平行四边形,
∴,,
在和中,
,
∴,
∴.
【点睛】本题考查了平行四边形的性质,全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.
19.B(5,0),C(8,),D(0,)
【分析】先根据勾股定理得到OD的长,即可得到点D的坐标,再根据平行四边形的性质即可得到点B、点C的坐标.
【详解】解:在Rt△ADO中,AD=6,AO=3,,
∴OD==,
∴D(0,),
∵平行四边形ABCD,
∴AB=CD=8,
∴B(5,0),C(8,).
【点睛】本题考查了坐标与图形,平行四边形的性质,解答本题的关键是熟练掌握平行于x轴的直线上的点的纵坐标相同,平行于y轴的直线上的点的横坐标相同.
20.证明见解析.
【分析】根据平行四边形的性质可得:AB=CD,AD∥BC,根据平行线性质和角平分线性质求出∠ABE=∠AEB,推出AB=AE,同理求出DF=CD,即可证明AE=DF.
【详解】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理可得:DF=CD,
∴AE=DF,
即AF+EF=DE+EF,
∴AF=DE.
【点睛】本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定等知识点的应用,能综合运用性质进行推理是解此题的关键,题目比较典型,难度适中.
21.(1)证明见解析
(2)2
【分析】本题主要考查了平行四边形的性质,等腰三角形的性质与判定, 角平分线的定义:
(1)先证明,得到,再根据,利用等腰三角形性质得到结论;
(2)根据平行四边形性质和,求出BE和AB,问题得解.
【详解】(1)证明:∵四边形是平行四边形,
,即,
,
平分,
,
,
又,
;
(2)解:四边形是平行四边形,
,
,
.
22.(1);(2);(3);拓展推广:阴影部分的面积;实践应用:三角形区域的面积.
【分析】(1)平行四边形的面积等于底乘以高,设平行四边形ABCD的高为h, △DCM边CD的高也为h,由题S平行四边形ABCD=CD×h,S△DCM=CD×h=S平行四边形ABCD=50;
(2)由(1)同理可得S△DCM =50;
(3)由(1)同理可得S△DCM =50;
拓展推广:由(1)的结论可得S△ADF=a, S△ABE=a,由此即可得阴影部分的面积;
应用,由推广的结论,有,,,由此即可求出三角形区域的面积.
【详解】 设平行四边形ABCD的边CD上的高为h,则△DCM边CD的高也为h,
∵S平行四边形ABCD=CD×h,则平行四边形的面积,
;
与同理可得;
与同理可得;
拓展推广:
根据的结论,,
,
∴阴影部分的面积;
实践应用:
根据前面信息,,
,
,
∴三角形区域的面积.
【点睛】本题考查了平行四边形的性质,等底同高的三角形的面积等知识,弄懂题意,结合图形、熟练运用相关知识是解题的关键.
23.AB=2.6cm,BC=1.7cm
【分析】由□ABCD的周长为8.6cm,可得,再由△ABD的周长为6cm,可得AD+AB+BD=6cm,即可得到BD=6-AD-AB=1.7cm,再由线段垂直平分线的性质得到,由此即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵□ABCD的周长为8.6cm,
∴AB+AD+BC+CD=8.6cm,
∴,
∵△ABD的周长为6cm,
∴AD+AB+BD=6cm,
∴BD=6-AD-AB=1.7cm,
∵E是AB的中点,DE⊥AB,
∴DE垂直平分线AB,
∴,
∴AB=4.3-AD=2.6cm.
【点睛】本题主要考查了平行四边形的性质,线段垂直平分线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
24.(1)详见解析;(2)
【分析】(1)根据题意平分可得,从而证明即可解答
(2)由(1)可知,再根据四边形是平行四边形可得,过点作延长线于点,再根据勾股定理即可解答
【详解】(1)证明:平分
又
又
(2)
四边形是平行四边形
,
为等边三角形
过点作延长线于点.
在中,
【点睛】此题考查三角形全等的判定与性质,勾股定理,平行四边形的性质,解题关键在于作好辅助线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.2平行四边形及其性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,,平分,交边于点E,则线段的长度分别是( )
A.2和3 B.3和2 C.4和1 D.1和4
2.如图所示,在中,的平分线交于点,若,,则的周长是( )
A.10 B.12 C.9 D.15
3.如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
A.100° B.95° C.90° D.85°
4.如图,在中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于( )
A.2 B.3 C.4 D.5
5.平行四边形的一组对角的平分线( )
A.一定相互平行 B.一定相交 C.可能平行也可能相交 D.平行或共线
6.如图,在中,E,F是对角线上的两点,则添加①;②;③;④中任意一个条件,能够使的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在 ABCD中,下列说法一定正确的是( )
A.AC=BD B.AC⊥BD C.AB=CD D.AB=BC
8.中,,则的度数是( )
A.20° B.30° C.40° D.150°
9.如图,平行四边形的对角线交于点,平分交于点,且,,连接.下列结论:①;②;③;④.其中成立的个数有( )
A.个 B.个 C.个 D.个
10.如图,在平行四边形ABCD中,∠BAD的平分线交CD于点G,AD=AE.若AD=5,DE=6,则AG的长是( )
A.6 B.8 C.10 D.12
11.如图,E是 ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是( )
A.AD=CF B.BF=CF C.AF=CD D.DE=EF
12.如图,在ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( ).
A.BO=DO B.CD=AB C.∠BAD=∠BCD D.AC=BD
二、填空题
13.在平行四边形中,的平分线把边分成5和7两部分,则平行四边形的周长是 .
14.如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=8,BC=12,则EF的长为 .
15.在ABCD中,AB<BC,已知∠B=30°,AB=2,将△ABC沿AC翻折至△AB′C,使点B′落在ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 .
16.如图,在□ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S□AEPH= .
17.如图,在等腰中,,顶点在的边上,已知,则 .
三、解答题
18.已知,如图,E、F分别为的边、上的点,且,求证:.
19.平行四边形ABCD,AD=6,AB=8,点A的坐标为(-3,0),求B、C、D各点的坐标.
20.已知:如图,在中,的平分线交于点,的平分线交于点,交于点.
求证:.
21.如图,在平行四边形中,的平分线与的延长线相交于点E,于点H.
(1)求证:;
(2)若,求的长.
22.问题探究:已知平行四边形的面积为,是所在直线上一点.
如图:当点与重合时,________;
如图,当点与与均不重合时,________;
如图,当点在(或)的延长线时,________.
拓展推广:如图,平行四边形的面积为,、分别为、延长线上两点,连接、、、,求出图中阴影部分的面积,并说明理由.
实践应用:如图是一平行四边形绿地,、分别平行于、,它们相交于点,,,,,现进行绿地改造,在绿地内部作一个三角形区域(连接、、,图中阴影部分)种植不同的花草,求出三角形区域的面积.
23.已知:如图,在□ABCD中,从顶点D向AB作垂线,垂足为E,且E是AB的中点,若□ABCD的周长为8.6cm,△ABD的周长为6cm,求AB、BC的长.
24.已知:如图,在平行四边形中,的平分线交于点,过点作的垂线交于点,交延长线于点,连接,.
(1)求证:;
(2)若,,, 求的长.
《4.2平行四边形及其性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C B D C C B B B
题号 11 12
答案 B D
1.B
【分析】本题主要考查了角平分线、平行四边形的性质及等腰三角形的判定,根据已知得出∠BAE=∠AEB是解决问题的关键.
先根据角平分线及平行线的性质得出,再由等角对等边得出,从而求出的长.
【详解】解:∵四边形是平行四边形,
∴,,
∴,
∵平分,,
∴,
∴,
∴,
∴,
故选:B.
2.A
【分析】在平行四边形ABCD中,根据对边平行且相等可得: ,又由BE是的平分线,可得,
易得AE=AB,即可求得的周长.
【详解】∵四边形ABCD是平行四边形
∴
∴
∵BE是的平分线
∴
∴
∴AE=AB=2
∵
∴
∴
∴的周长为10
故选:A
【点睛】本题考查的知识点主要是平行四边形的性质,解题中结合等腰三角形的判定“等边对等角”是关键.
3.C
【详解】在中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
4.B
【分析】由四边形ABCD为平行四边形,得到AD与BC平行,AD=BC,利用两直线平行得到一对内错角相等,由BE为角平分线得到一对角相等,等量代换得到∠ABE=∠AEB,利用等角对等边得到AB=AE=4,由AD﹣AE求出ED的长即可.
【详解】解:∵四边形ABCD为平行四边形,
∴AD//BC,AD=BC=7,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE=4,
∴ED=AD﹣AE=BC﹣AE=7﹣4=3.
故选:B.
【点睛】此题考查了角平分线的定义,等腰三角形的判定,以及平行四边形的性质,熟练掌握平行四边形的性质是解本题的关键.
5.D
【分析】分两种情况:如果平行四边形的邻边不相等,那么它的一组对角的平分线互相平行;如果平行四边形的邻边相等,那么它的一组对角的平分线共线.
【详解】解:如图,中,AE、CF分别平分∠BAD、∠BCD,
∵四边形ABCD是平行四边形,AD∥BC,
∴∠BAD=∠BCD,∠2=∠3,
∵AE、CF分别平分∠BAD、∠BCD,
∴,
∴∠2=∠4,
∴∠3=∠4,
∴AE∥CF;
当是菱形时,AE与CF共线.
故选:D.
【点睛】本题主要考查了平行四边形的性质,角平分线的定义,平行线的判定,将平行四边形分类讨论是解决本题的关键.
6.C
【分析】本题考查了全等三角形的判定定理,熟练掌握全等三角形的判定定理是解题的关键;根据全等三角形的判定定理,逐项判断即可.
【详解】∵四边形是平行四边形,
∴,
∴,
当时,由可证,所以①符合题意;
当时,可得,即,由可证,所以②符合题意;
当时,不能判定,所以③不符合题意;
当时,由可证,所以④符合题意.
∴满足题意的有3个.
故选:C.
7.C
【详解】解:∵平行四边形的两组对边分别平行且相等,对角线互相平分,
∴C正确,其余不一定正确,
故选C.
8.B
【分析】本题考查平行四边形的性质,掌握平行四边形邻角互补对角相等是解题的关键,根据平行四边形的性质可知,,结合可求出,从而得解.
【详解】在中,,,
又∵,
∴,
∴,
故选:B.
9.B
【分析】此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质,证得是等边三角形以及是的中位线是解答本题的关键.
由中,,易得是等边三角形,又由,证得;继而证得,得;由、以及,可得;可得是三角形的中位线,证得.
【详解】解:四边形是平行四边形,
,,
平分,
,
是等边三角形,
,
,
,
,
,故正确;
,
,故正确;
,,
,
,故错误;
,,,
,
,
,
,
,故错误;
故选:B.
10.B
【分析】由等腰三角形的角平分线性质得到DH=EH=3,由平行四边形的性质和平行线的性质得到DA=DG,AH=GH,再由勾股定理AH=,从而得到正确答案.
【详解】如图,设AG交BD于H.
∵AD=AE,AG平分∠BAD,
∴AG垂直平分DE,
∴DH=EH=3,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠AGD=∠GAB,
∵∠DAG=∠GAB,
∴∠DAG=∠DGA,
∴DA=DG,
∵DE⊥AG,
∴AH=GH,
在Rt△ADH中,AH===4,
∴AG=2AH=8.
故选B.
【点睛】本题考查了平行四边形的性质、等腰三角形的角平分线性质、勾股定理和平行线的性质,解题的关键是推得DA=DG 和AH=GH.
11.B
【详解】∵ABCD是平行四边形,∴AD=BC,∠B=∠D,AB∥CD.∵BF∥CD,∴∠F=∠FCD,∠FAE=∠D.∵AE=ED,∴△AEF≌△DEC.∴AF=CD,EF=CE.∵∠FCD=∠D,∴CE=DE.∴DE=EF.故C、D都成立;∵∠B=∠D=∠F,则CF=BC=AD.故A成立.没有条件证明BF=CF.
12.D
【分析】根据平行四边形的性质判断即可
【详解】解:A、∵四边形ABCD是平行四边形,
∴OB=OD(平行四边形的对角线互相平分),正确,不符合题意;
B、∵四边形ABCD是平行四边形,
∴CD=AB(平行四边形的对边相等),正确,不符合题意;
C、∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD(平行四边形的对角相等),正确,不符合题意;
D、根据四边形ABCD是平行四边形不能推出AC=BD,错误,符合题意.
故选D.
13.34或38
【分析】本题主要考查了平行四边形的性质,等腰三角形的判定,三角形的角平分线等知识点,解此题的关键是求出.分类讨论.
由平行四边形推出,由已知得到,推出,分两种情况(1)当时,;(2)当时,求.
【详解】解:∵平行四边形中,的平分线把边分成5和7两部分,
∴,
∵,
∴,
∴,
∴,
∴当时,平行四边形的周长是,
当时,平行四边形的周长是,
∴平行四边形的周长是34或38.
故答案为:34或38.
14.4
【分析】根据平行四边形的性质可得,由角平分线可得,所以,所以,同理可得,则根据即可求解.
【详解】∵四边形是平行四边形,
∴,,,
∴,
∴平分,
∴,
∴,
∴,
同理可得,
∴.
故答案为:4
【点睛】本题主要考查了平行四边形的性质、角平分线的定义,转化线段是解题的关键.
15.4或6.
【详解】试题分析:本题主要考查了翻折变换的性质,解题的关键是画出图形,发现存在两种情况,进行分类讨论.在ABCD中,AB<BC,要使△AB′D是直角三角形,有两种情况:∠B′AD=90°或∠AB′D=90°,画出图形,分类讨论:(1)当∠B′AD=90°AB<BC时,如图1,延长B′A交BC于点G,利用平行四边形和直角三角形的性质,可求出BC的长为6;(2)当∠AB′D=90°时,如图2,由平行四边形的性质可求出四边形ACDB′是等腰梯形,然后根据∠AB′D=90°,得出四边形ACDB′是矩形,再通过解直角三角形,得出BC的长为4.
解:当∠B′AD=90°AB<BC时,如图1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2,
∴∠AB′C=30°,
∴GC=B′C=BC,
∴G是BC的中点,
在RT△ABG中,BG=AB=×2=3,
∴BC=6;
当∠AB′D=90°时,如图2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2,
∴BC=AB÷=2×=4,
∴当BC的长为4或6时,△AB′D是直角三角形.
故答案为4或6.
考点:1.翻折变换(折叠问题);2.平行四边形的性质;3.等腰梯形、矩形和直角三角形.
16.4
【分析】由条件可证明四边形HPFD、BEPG为平行四边形,可证明S四边形AEPH=S四边形PFCG.,再利用面积的和差可得出四边形AEPH和四边形PFCG的面积相等,由已知条件即可得出答案.
【详解】解:∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG、AEPH、CFPG为平行四边形,
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD-S△PEB-S△PHD=S△CDB-S△BGP-S△DFP,
即S四边形AEPH=S四边形PFCG.
∵CG=2BG,S△BPG=1,
∴S四边形AEPH=S四边形PFCG=4×1=4;
故答案为:4.
【点睛】本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行 四边形为平行四边形,②两组对边分别相等 四边形为平行四边形,③一组对边平行且相等 四边形为平行四边形,④两组对角分别相等 四边形为平行四边形,⑤对角线互相平分 四边形为平行四边形.
17.110
【分析】先根据等腰三角形的性质求出∠ABC的度数;再根据平行四边形对边平行和两直线平行同旁内角互补的性质,得出∠2+∠ABE=180 ,代入求解即可.
【详解】解:∵是等腰三角形,∠A=120 ,
∴∠ABC=∠C=(180 -∠A)÷2=30 ,
∵四边形是平行四边形,
∴OFDE,
∴∠2+∠ABE=180 ,
即∠2+30 +40 =180 ,
∴∠2=110 .
故答案为:110 .
【点睛】此题考查了等腰三角形的性质和平行四边形的性质,解题的关键是数形结合,熟练运用上述知识求解.
18.见详解
【分析】根据条件证明,即可得出结论.
【详解】证明:∵四边形是平行四边形,
∴,,
在和中,
,
∴,
∴.
【点睛】本题考查了平行四边形的性质,全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.
19.B(5,0),C(8,),D(0,)
【分析】先根据勾股定理得到OD的长,即可得到点D的坐标,再根据平行四边形的性质即可得到点B、点C的坐标.
【详解】解:在Rt△ADO中,AD=6,AO=3,,
∴OD==,
∴D(0,),
∵平行四边形ABCD,
∴AB=CD=8,
∴B(5,0),C(8,).
【点睛】本题考查了坐标与图形,平行四边形的性质,解答本题的关键是熟练掌握平行于x轴的直线上的点的纵坐标相同,平行于y轴的直线上的点的横坐标相同.
20.证明见解析.
【分析】根据平行四边形的性质可得:AB=CD,AD∥BC,根据平行线性质和角平分线性质求出∠ABE=∠AEB,推出AB=AE,同理求出DF=CD,即可证明AE=DF.
【详解】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理可得:DF=CD,
∴AE=DF,
即AF+EF=DE+EF,
∴AF=DE.
【点睛】本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定等知识点的应用,能综合运用性质进行推理是解此题的关键,题目比较典型,难度适中.
21.(1)证明见解析
(2)2
【分析】本题主要考查了平行四边形的性质,等腰三角形的性质与判定, 角平分线的定义:
(1)先证明,得到,再根据,利用等腰三角形性质得到结论;
(2)根据平行四边形性质和,求出BE和AB,问题得解.
【详解】(1)证明:∵四边形是平行四边形,
,即,
,
平分,
,
,
又,
;
(2)解:四边形是平行四边形,
,
,
.
22.(1);(2);(3);拓展推广:阴影部分的面积;实践应用:三角形区域的面积.
【分析】(1)平行四边形的面积等于底乘以高,设平行四边形ABCD的高为h, △DCM边CD的高也为h,由题S平行四边形ABCD=CD×h,S△DCM=CD×h=S平行四边形ABCD=50;
(2)由(1)同理可得S△DCM =50;
(3)由(1)同理可得S△DCM =50;
拓展推广:由(1)的结论可得S△ADF=a, S△ABE=a,由此即可得阴影部分的面积;
应用,由推广的结论,有,,,由此即可求出三角形区域的面积.
【详解】 设平行四边形ABCD的边CD上的高为h,则△DCM边CD的高也为h,
∵S平行四边形ABCD=CD×h,则平行四边形的面积,
;
与同理可得;
与同理可得;
拓展推广:
根据的结论,,
,
∴阴影部分的面积;
实践应用:
根据前面信息,,
,
,
∴三角形区域的面积.
【点睛】本题考查了平行四边形的性质,等底同高的三角形的面积等知识,弄懂题意,结合图形、熟练运用相关知识是解题的关键.
23.AB=2.6cm,BC=1.7cm
【分析】由□ABCD的周长为8.6cm,可得,再由△ABD的周长为6cm,可得AD+AB+BD=6cm,即可得到BD=6-AD-AB=1.7cm,再由线段垂直平分线的性质得到,由此即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵□ABCD的周长为8.6cm,
∴AB+AD+BC+CD=8.6cm,
∴,
∵△ABD的周长为6cm,
∴AD+AB+BD=6cm,
∴BD=6-AD-AB=1.7cm,
∵E是AB的中点,DE⊥AB,
∴DE垂直平分线AB,
∴,
∴AB=4.3-AD=2.6cm.
【点睛】本题主要考查了平行四边形的性质,线段垂直平分线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
24.(1)详见解析;(2)
【分析】(1)根据题意平分可得,从而证明即可解答
(2)由(1)可知,再根据四边形是平行四边形可得,过点作延长线于点,再根据勾股定理即可解答
【详解】(1)证明:平分
又
又
(2)
四边形是平行四边形
,
为等边三角形
过点作延长线于点.
在中,
【点睛】此题考查三角形全等的判定与性质,勾股定理,平行四边形的性质,解题关键在于作好辅助线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
