4.3中心对称同步练习（含解析）

中小学教育资源及组卷应用平台
4.3中心对称
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，线段AC与BD相交于点O，且△ABO和△CDO关于点O成中心对称，则下列结论，其中正确的个数是（ ）
①OB＝OD；②AB＝CD；③；④AC＝BD．
A．4 B．3 C．2 D．1
2．下列语句正确的是( )
A．线段绕着它的中点旋转180°后与原线段重合，那么线段是中心对称图形
B．正三角形绕着它的三边中线的交点旋转120°后与原图形重合，则正三角形是中心对称图形
C．正方形绕着它的对角线交点旋转90°后与原图形重合，则正方形是中心对称图形
D．正五角星绕着它的中心旋转72°后与原图形重合，则正五角星是中心对称图形
3．平面直角坐标系内，把一个三角形的各顶点的横、纵坐标都乘以，则以这三个新坐标为顶点的三角形与原三角形（　　）
A．关于轴对称 B．关于轴对称 C．关于原点对称 D．关于直线对称
4．晋商大院的许多窗格图案蕴含着对称之美，现从中选取以下四种窗格图案，其中是中心对称图形但不是轴对称图形的是（ ）
A． B．
C． D．
5．2022年冬奥会将在我国北京市和张家口市联合举行，下列历届冬奥会会徽的部分图案中，是中心对称图形的是（　　）
A． B． C． D．
6．如图，两个半圆分别以P、Q为圆心，它们成中心对称，点A1，P，B1，B2，Q，A2在同一条直线上，则对称中心为（ ）
A．A2P的中点 B．A1B2的中点 C．A1Q的中点 D．PQ的中点
7．下列各式中，是中心对称图形的是（ ）
A． B． C． D．
8．已知点A（，1）与点A′（5，）关于坐标原点对称，则实数、的值是（ ）
A． B． C． D．
9．以下四个图案中，既是轴对称图形又是中心对称图形的有（ ）
A．4 B．3
C．2 D．1
10．在平面直角坐标系中，点关于原点对称的点的坐标是（ ）
A． B． C． D．
11．如果把三角形各顶点的纵、横坐标都乘以，得到，则这两个三角形在坐标中的位置关系是（ ）
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．无对称关系
12．下面图形中既是轴对称图形又是中心对称图形的是（）
A． B． C． D．
二、填空题
13．已知点与点关于原点对称，则 ， ．
14．点（1，2）关于原点的对称点的坐标为 ．
15．已知点与点关于原点对称，则点的坐标是 ．
16．在等腰三角形、平行四边形、矩形、菱形、正方形这五种图形中，既是轴对称图形，又是中心对称图形的有 种
17．在直角坐标系中，已知点和点关于原点对称，则的值是 ．
三、解答题
18．已知点与点关于原点对称，求，的值．
19．射线是不是中心对称图形？为什么？
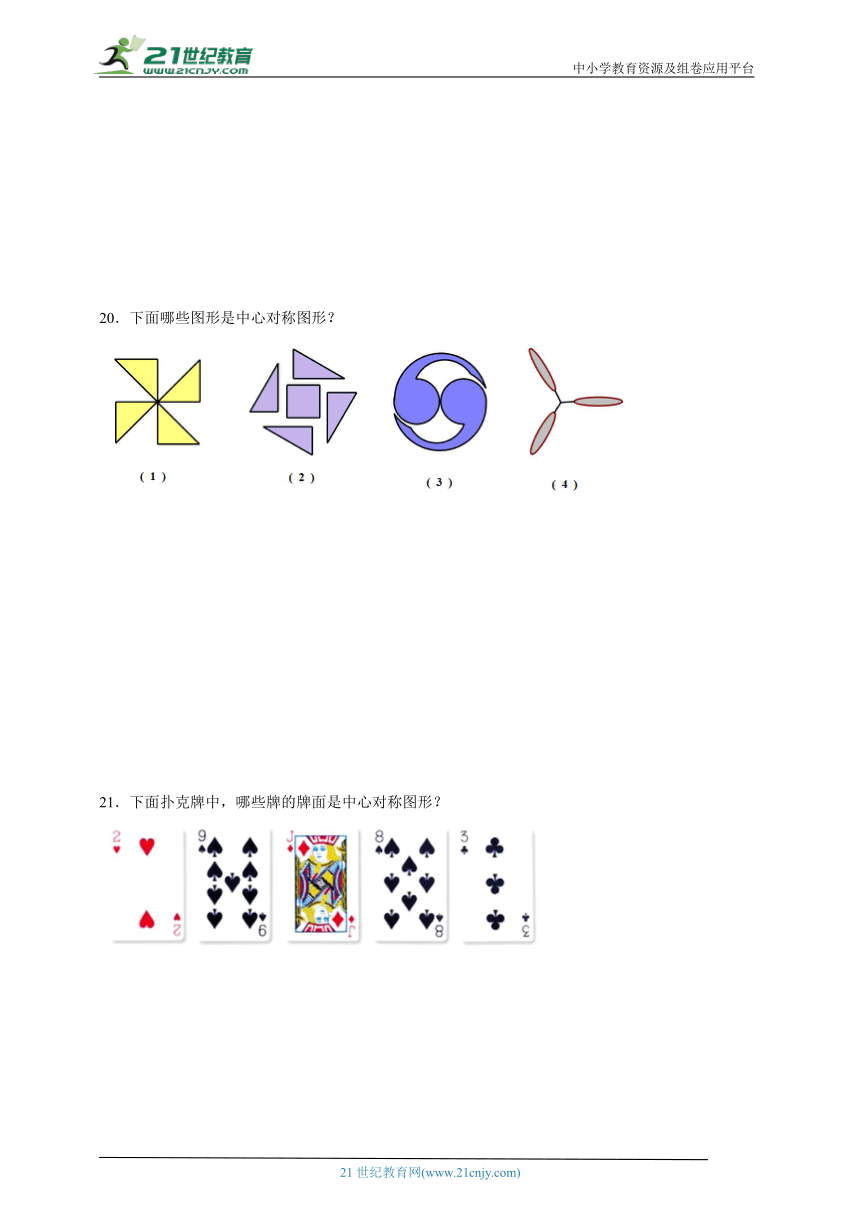
20．下面哪些图形是中心对称图形？
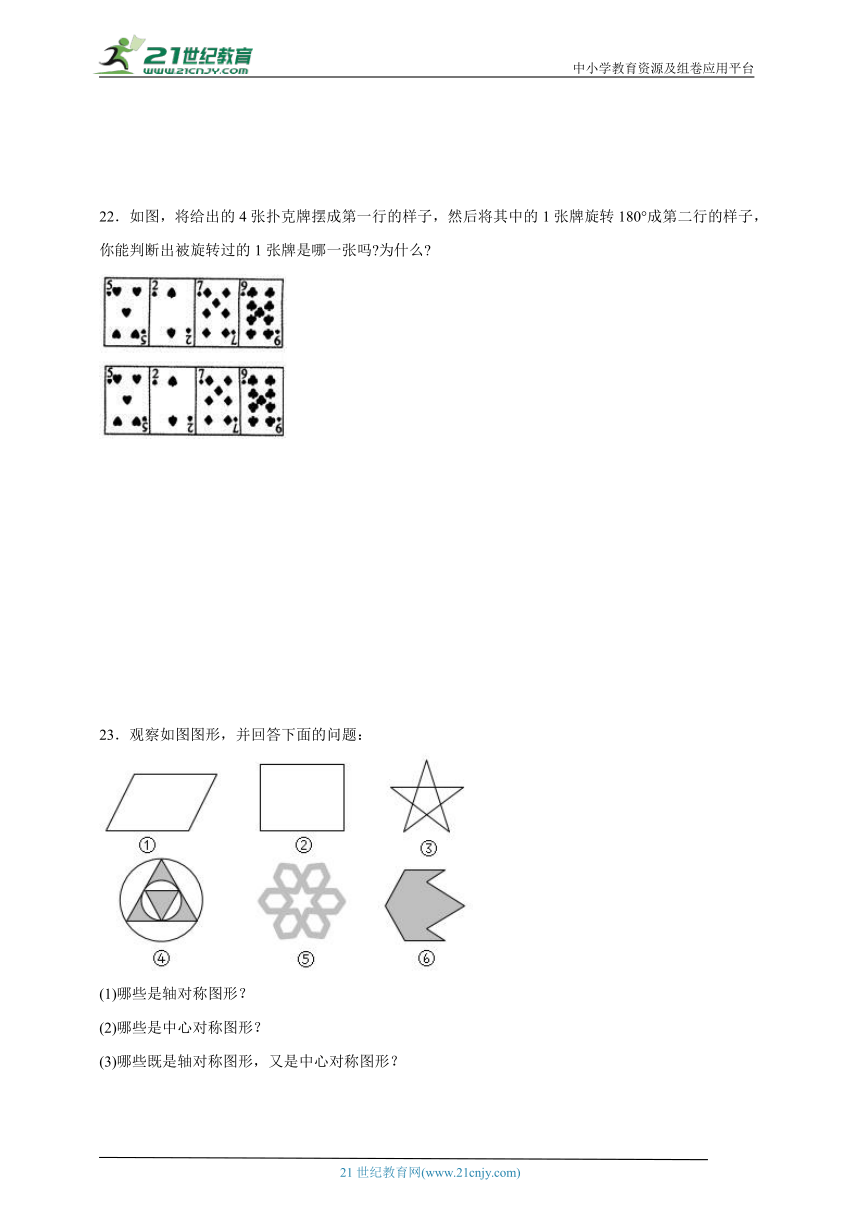
21．下面扑克牌中，哪些牌的牌面是中心对称图形？
22．如图，将给出的4张扑克牌摆成第一行的样子，然后将其中的1张牌旋转180°成第二行的样子，你能判断出被旋转过的1张牌是哪一张吗 为什么
23．观察如图图形，并回答下面的问题：
(1)哪些是轴对称图形？
(2)哪些是中心对称图形？
(3)哪些既是轴对称图形，又是中心对称图形？
24．用六根一样长的小棒搭成如图所示的图形.
(1)试移动AC，BC这两根小棒，使六根小棒成为中心对称图形；
(2)若移动AC，DE这两根，能不能也达到要求呢？(画出图形)
《4.3中心对称》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C B C D D D C C
题号 11 12
答案 C A
1．B
【分析】根据成中心对称的两个图形的性质解答．
【详解】解：∵△ABO和△CDO关于点O成中心对称，
∴△ABO≌△CDO，
∴OB＝OD，AB＝CD，
而AC＝BD不一定成立，
故选：B．
【点睛】此题考查成中心对称的两个图形的性质：成中心对称的两个图形全等，熟记性质是解题的关键．
2．A
【分析】根据中心对称图形的定义依次分析各项即可．
【详解】解：根据中心对称图形的定义可知A正确，B、C、D错误，
故选A．
【点睛】解答本题的关键是熟练掌握中心对称图形的定义：在同一平面内，如果把一个图形绕某一点旋转180°，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．
3．C
【分析】根据“关于原点对称的点，横、纵坐标互为相反数”，可知所得的三角形与原三角形关于原点对称．
【详解】解：∵一个三角形的各顶点的横、纵坐标都乘以，
∴这个三角形各个顶点与原三角形各个顶点关于原点对称，
∴这三个新坐标为顶点的三角形与原三角形关于原点对称．
故选：C．
【点睛】主要考查了平面直角坐标系中对称点的规律．解决本题的关键是掌握好对称点的坐标规律．
4．B
【分析】中心对称是指把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称；在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形．
【详解】解：A.既是中心对称图形也是轴对称图形，故A不符合题意；
B.是中心对称图形但不是轴对称图形，故B符合题意；
C.既是中心对称图形也是轴对称图形，故C不符合题意；
D.既是中心对称图形也是轴对称图形，故D不符合题意，
故选：B．
【点睛】本题考查中心对称图形与轴对称图形的识别，是基础考点，掌握相关知识是解题关键．
5．C
【分析】把一个图形绕某一点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，根据中心对称图形的概念求解．
【详解】解：A．不是中心对称图形，故本选项不符合题意；
B．不是中心对称图形，故本选项不符合题意；
C．是中心对称图形，故本选项符合题意；
D．不是中心对称图形，故本选项不符合题意．
故选：C．
【点睛】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．
6．D
【分析】由已知两个图形的位置，判断它们是否中心对称，可以把各对应点连线，看所有连线是否交于同一点．
【详解】解：如图对称中心是PQ的中点，
故选：D．
【点睛】本题考查了中心对称，正确的作出图形是解题的关键．
7．D
【分析】根据中心对称图形的定义逐一判断即可．
【详解】解：A．不是中心对称图形，故A错误；
B．不是中心对称图形，故B错误；
C．不是中心对称图形，故C错误；
D．是中心对称图形，故D正确．
故选：D．
【点睛】本题主要考查了中心对称图形的定义，熟练掌握中心对称图形的定义，把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
8．D
【详解】试题分析：已知点A（a，1）与点A′（5，b）关于坐标原点对称，根据关于原点对称的点的横坐标与纵坐标互为相反数可得a＝－5，b＝－1，故答案选D．
考点：关于原点对称的点的坐标．
9．C
【分析】根据轴对称图形与中心对称图形的概念求解．在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与自身重合是中心对称图形，在平面内沿一条直线折叠，直线两旁的部分能够完全重合的图形是轴对称图形，这条直线就叫做对称轴．
【详解】第一个图：是轴对称图形，不是中心对称图形，不合题意；
第二个图：不是轴对称图形，也不是中心对称图形，不合题意；
第三个图：是轴对称图形，也是中心对称图形，符合题意；
第四个图：是轴对称图形，也是中心对称图形，符合题意．
故选：C．
【点睛】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
10．C
【分析】根据关于原点对称的点的坐标特点解答．
【详解】解：点P（-3，-5）关于原点对称的点的坐标是（3，5），
故选：C．
【点睛】本题考查的是关于原点的对称的点的坐标，平面直角坐标系中任意一点P（x，y），关于原点的对称点是（-x，-y），即关于原点的对称点，横纵坐标都变成相反数．
11．C
【分析】根据“关于原点对称的点的横坐标和纵坐标互为相反数解答”．
【详解】解：纵、横坐标都乘以-1后，相对应的各点的横纵坐标均互为相反数，那么对应点关于原点对称，则这两个三角形在坐标中的位置关系是关于原点对称．
故选C．
【点睛】横纵坐标均互为相反数的点关于原点对称，那么对应点所在的图形也关于原点对称．
12．A
【分析】本题主要考查了轴对称图形和中心对称图形，熟练掌握如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形；在平面内，把一个图形绕着某个点旋转，如果旋转后的图形能与原来的图形重合那么这个图形叫做中心对称图形是解题的关键；
根据轴对称图形和中心对称图形的定义，逐项判断即可求解；
【详解】解：A、既是轴对称图形又是中心对称图形，故本选项符合题意；
B、是轴对称图形，但不是中心对称图形，故本选项不符合题意；
C、既不是轴对称图形，也不是中心对称图形，故本选项不符合题意；
D、是中心对称图形，但不轴对称图形，故本选项不符合题意；
故选：A．
13． -1 -4
【分析】根据关于原点对称的点的坐标特征：横坐标、纵坐标都互为相反数列方程即可得答案．
【详解】∵点与点关于原点对称，
∴m-1=-2，n+1=-3，
解得：m=-1，n=-4，
故答案为：-1，-4
【点睛】本题考查关于原点对称的点坐标的特征，关于原点对称的点的坐标特点是横坐标、纵坐标都互为相反数；是需要熟记的基本问题，记忆方法可以结合平面直角坐标系的图形．
14．
【分析】根据关于原点的对称点，横纵、坐标都互为相反数解答．
【详解】解：点关于原点的对称点的坐标为．
故答案为：．
【点睛】本题考查了关于原点对称的点的坐标，解题的关键是熟记“关于原点的对称点，横纵、坐标都互为相反数”．
15．
【分析】本题考查了关于原点对称的点的坐标特征，根据关于原点对称的点的坐标的横、纵坐标均互为相反数即可得出答案．
【详解】解：点与点关于原点对称，
点的坐标是，
故答案为：．
16．3
【分析】本题考查了轴对称图形与中心对称图形的概念．根据轴对称图形与中心对称图形的概念求解．
【详解】等腰三角形是轴对称图形，平行四边形是中心对称图形，矩形、菱形、正方形既是轴对称图形，又是中心对称图形．
故答案为：3．
17．-1
【分析】直接利用关于原点对称点的性质得出关于a，b的方程组，进而得出答案．
【详解】解：点和点关于原点对称，
，
解得：，
则的值是：．
故答案为：．
【点睛】此题主要考查了关于原点对称点的性质，正确得出a，b的值是解题关键．
18．a ＝－5，b ＝－1．
【分析】点A（a，1）与点A′（5，b）是关于原点对称，可知，两点的横纵坐标均互为相反数．由此即可得到a和b的值．
【详解】解：根据已知条件，点A（a，1）与点A′（5，b）是关于原点对称，
所以有a＝ 5，b＝ 1．
【点睛】本题考查了关于原点对称的点的坐标，掌握两点关于原点对称，则两点的横、纵坐标都是互为相反数是解题关键．
19．不是，见解析
【分析】根据中心对称图形的定义判断射线是不是中心对称图形．
【详解】解：不是，
理由是：射线绕着一点旋转180°不能与自身重合，故射线不是中心对称图形．
【点睛】本题考查中心对称图形的判断，解题的关键是掌握中心对称图形的定义．
20．（1）（2）（3）
【分析】根据中心对称图形的概念进行判断即可．
【详解】解：（1）是中心对称图形，符合题意；
（2）是中心对称图形，符合题意；
（3）是中心对称图形，符合题意；
（4）不是中心对称图形，不合题意．
【点睛】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．掌握中心对称图形与轴对称图形的概念是解题关键．
21．“红桃2”“方片J”的牌面图案是中心对称图形
【分析】根据中心对称图形的概念进行判断即可．
【详解】解：“红桃2” 的牌面图案是中心对称图形，符合题意；
“黑桃9” 的牌面图案不是中心对称图形，不符合题意；
“方片J” 的牌面图案是中心对称图形，符合题意；
“黑桃8” 的牌面图案不是中心对称图形，不符合题意；
“梅花3” 的牌面图案不是中心对称图形，不符合题意．
综合所述：“红桃2”“方片J”的牌面图案是中心对称图形．
【点睛】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．掌握中心对称图形与轴对称图形的概念是解题关键．
22．第2张，因为是中心对称图形
【分析】观察，根据中心对称图形的概念解答即可.
【详解】被旋转过的1张牌是第二张牌．
理由如下：第一张牌，因为最中间的图案不是中心对称，所以不是中心对称图形，第二张牌是中心对称图形，第三张牌，因为最中间只有一个方块，所以不是中心对称图形，第四张牌，因为最中间的图案不是中心对称，所以不是中心对称图形，
∵将其中的1张牌旋转180°成第二行的样子，
∴被旋转过的1张牌是第二张．
23．(1)②③④⑤⑥
(2)①②⑤
(3)②⑤
【分析】（1）根据轴对称图形的定义即可求解；
（2）根据中心对称图形的定义即可求解；
（3）综合（1）（2）结论即可求解．
【详解】（1）解：根据轴对称图形的定义，②③④⑤⑥是轴对称图形；
（2）解：根据中心对称图形的定义，①②⑤是中心对称图形；
（3）解：由（1）（2）可知，②⑤既是轴对称图形，又是中心对称图形．
【点睛】本题考查轴对称图形和中心对称图形的识别，解题的关键是掌握定义．一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形是轴对称图形；在平面内，把一个图形绕着某个点旋转180度，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．
24．(1)如图： 将AC、BC分别移动到AC′、BC′处．
(2)能，如图 将AC、DE分别移动到BC′、BE′处．
【分析】（1）A、D关于点B中心对称，所以找到E关于点B的中心对称点C′，连接A、C′，B、C′即可．
（2）A、D关于点B中心对称，所以找到C、E关于点B的中心对称点C′、E′，连接B、 C′，B、E′即可．
【详解】（1）如图：延长EB，使BC′=BE，连接A、C′
∵BE=BC′， C′、B、E在同一条直线上
∴E、C′关于点B中心对称
∵A、C关于点B中心对称
∴△AC′B和△DEB关于点B中心对称
∴所得图形是关于点B对称的中心对称图形．
（2）能，如图：
延长CB、EB，使CB=BC′，EB=BE′
∵C、B、C′在同一条直线上，E、B、E′在同一条直线上，CB=BC′，EB=BE′
∴C、C′，E、E′分别关于点B中心对称
∵A、D关于点B中心对称
∴此图形为中心对称图形，对称中心为点B．
【点睛】本题考查了中心对称图形的定义，熟练掌握中心对称图形的相关知识，准确绘图是本题的解题关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)