第一章解直角三角形同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
A. B. C.sin37° D.cos37°
2.的倒数为( )
A. B. C. D.
3.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为( ).
A. B. C. D.
4.如图,为的直径,弦交于点E,,则( )
A. B.1 C. D.2
5.如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
6.利用科学计算器计算,下列按键顺序正确的是( )
A.
B.
C.
D.
7.的值等于( )
A. B. C. D.
8.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
9.在平面直角坐标系中,直线与轴交于点,与轴交于点,将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接,则的长度为( )
A. B. C.2 D.
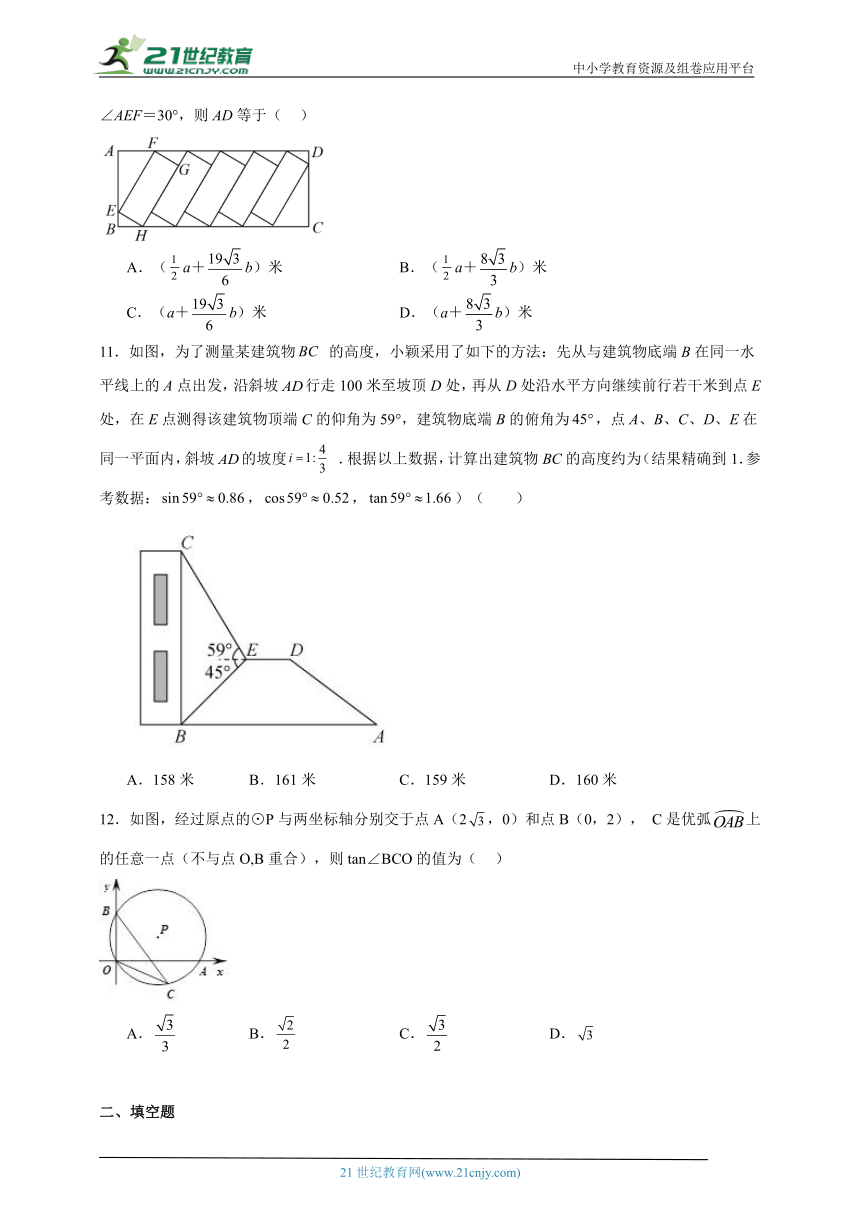
10.如图,在一块矩形ABCD区域内,正好划出5个全等的矩形停车位,其中EF=a米,FG=b米,∠AEF=30°,则AD等于( )
A.(a+b)米 B.(a+b)米
C.(a+b)米 D.(a+b)米
11.如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡行走100米至坡顶D处,再从D处沿水平方向继续前行若干米到点E处,在E点测得该建筑物顶端C的仰角为59°,建筑物底端B的俯角为,点A、B、C、D、E在同一平面内,斜坡的坡度 .根据以上数据,计算出建筑物BC的高度约为(结果精确到1.参考数据:,,)( )
A.158米 B.161米 C.159米 D.160米
12.如图,经过原点的⊙P与两坐标轴分别交于点A(2,0)和点B(0,2), C是优弧上的任意一点(不与点O,B重合),则tan∠BCO的值为( )
A. B. C. D.
二、填空题
13.在锐角中,如果,满足,那么 .
14.如图,已知梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,则斜坡AB的长为 m.
15.比较大小:sin48° cos48°(填“>”、“<”或“=”).
16.如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是 .
17.如图,在△ABC中,∠C=90°,BC:AC=1:2,则sinA= ,cosA= ,tanB= .
三、解答题
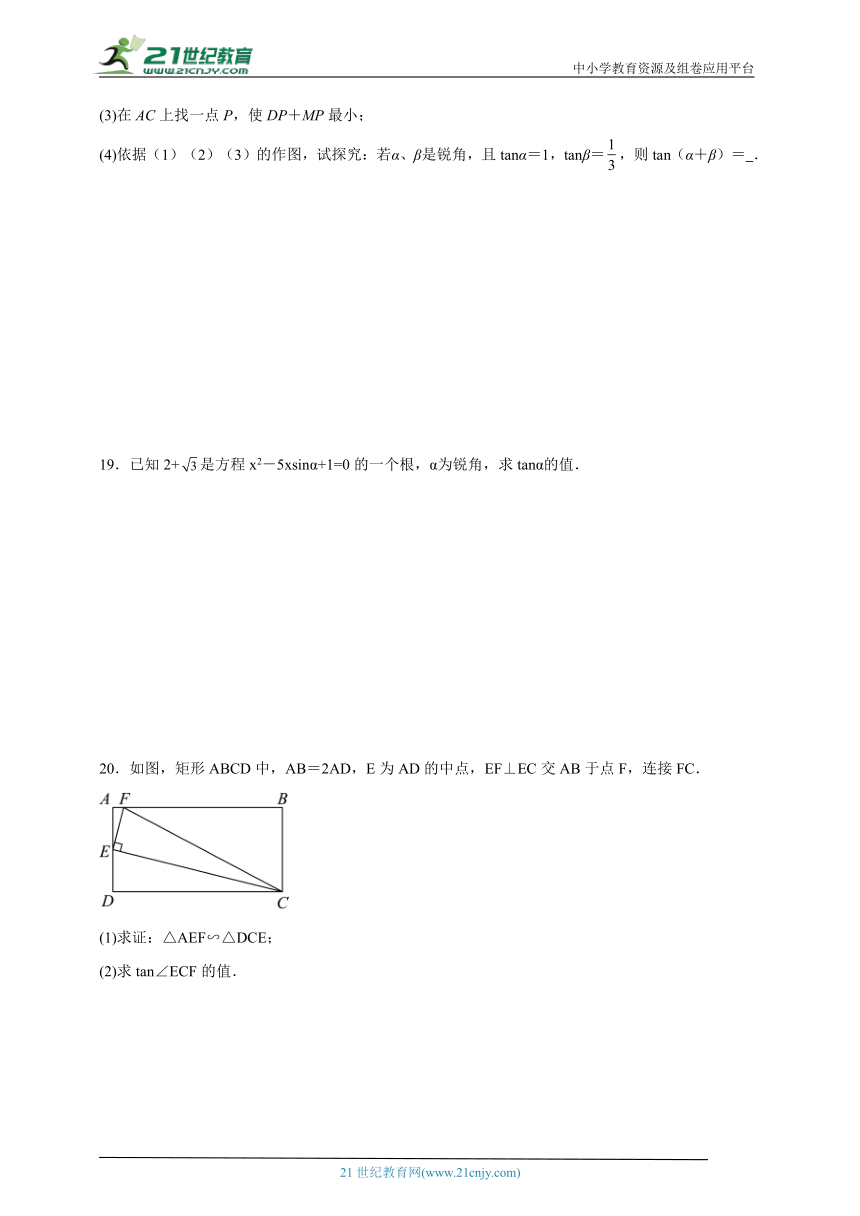
18.如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点,△ABC的三个顶点在格点上,仅用无刻度的直尺在网格中画图,画图过程用虚线表示.
(1)将边BC绕点C逆时针旋转90°得到线段CD;
(2)在线段CD上找一点M,使得AMBC;
(3)在AC上找一点P,使DP+MP最小;
(4)依据(1)(2)(3)的作图,试探究:若α、β是锐角,且tanα=1,tanβ=,则tan(α+β)= .
19.已知2+是方程x2-5xsinα+1=0的一个根,α为锐角,求tanα的值.
20.如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
21.在一个三角形中,各边和它所对角的正弦的比相等.即.利用上述结论可以求解如下题目.如:
在中,若,,,求.
解:在中,
问题解决:
如图,甲船以每小时海里的速度向正北方航行,当甲船位于处时,乙船位于甲船的北偏西方向的处,且乙船从处按北偏东方向匀速直线航行,当甲船航行分钟到达处时,乙船航行到甲船的北偏西方向的处,此时两船相距海里.
(1)判断的形状,并给出证明.
(2)乙船每小时航行多少海里?
22.如图,甲船在港口P的南偏东60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度驶向港口P;乙船从港口P出发,沿南偏西45°方向驶离港口P.现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向,求乙船的航行距离.(,,结果保留整数).
23.如图,已知中,,,,边的垂直平分线分别交、于点、.求线段的长.
24.如图,甲船在港口P的南偏西60°方向,距港口80海里的A处,沿AP方向以每小时18海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,已知两船同时出发,经过2小时乙船恰好在甲船的正东方向.求乙船的行驶速度.(结果保留根号)
《第一章解直角三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B A A A B A
题号 11 12
答案 D A
1.B
【分析】过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CDAC=40海里,再解Rt△CBD中,得出BC海里,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.
【详解】如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80,∴CDAC=40.
在Rt△CBD中,∵∠CDB=90°,∠BCD=37°,∴BC,∴海警船到大事故船C处所需的时间大约为:40(小时).
故选B.
【点睛】本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.
2.A
【分析】根据特殊角的三角函数值以及倒数的定义即可求解.
【详解】解:,的倒数是
∴的倒数为,
故选:A.
【点睛】本题考查了特殊角的三角函数值以及倒数的定义,熟练掌握特殊角的三角函数值以及倒数的定义是解题的关键.
3.A
【分析】
在中,,由此可以求出之长.
【详解】
解:在中,
,
.
又,,
.
故选:.
【点睛】此题考查了正切的概念和运用,关键是把实际问题转化成数学问题,把它抽象到直角三角形中来.
4.B
【分析】根据为的直径,可证出,再根据已知和三角函数即可得出和,进而即可得解.
【详解】解:∵为的直径,,
∴,
∴,
∵,
∴,
∵为的直径,
∴,
∴,
∴,
∴.
故选:B.
【点睛】本题考查的是圆周角定理的应用,垂径定理推论的应用,锐角三角函数的应用,熟练的运用锐角三角函数求解的长是解本题的关键.
5.B
【详解】解:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,
根据勾股定理的逆定理可知∠ABC=90°,
根据平行线的性质可得:∠ABE=110°,
则∠CBE=110°-90°=20°,
即点C在点B的北偏西20°方向上.
故选B
6.A
【分析】简单的电子计算器工作顺序是先输入者先算,根据按键顺序写出式子,再根据开方运算即可求出显示的结果.
【详解】
解:利用该型号计算器计算 ,按键顺序正确的是:
故选:A.
【点睛】本题主要考查了计算器-三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
7.A
【详解】3cos60°=3×=.
故选A.
点睛:熟记特殊角的三角函数值.
8.A
【分析】根据锐角A的邻边a与对边b的比叫做∠A的余切,记作cotA.
【详解】解:∵∠C=90°,
∴=,
故选:A.
【点睛】此题主要考查了锐角三角函数的定义,关键是掌握余切定义.
9.B
【分析】先求出点A、B的坐标,可求得OA、OB,进而可求得∠OAB=60°,利用旋转的性质和等边三角形的判定与性质证明和为等边三角形得到即可求解.
【详解】解:对于,
当时,,当时,由得:,
则A(1,0),B(0,),
∴,,
∴,则∠OAB=60°,
由旋转性质得:,,,
∴是等边三角形,
∴,又
∴是等边三角形,
∴,
故选:B.
【点睛】本题考查一次函数图象与坐标轴的交点问题、旋转性质、等边三角形的判定与性质、解直角三角形,熟练掌握相关知识的联系与运用,证得是等边三角形是解答的关键.
10.A
【分析】在Rt△AEF中,通过解直角三角形求得AF,再在Rt△FMG和Rt△DQK中,通过解直角三角形求得FM,最后由AD=AF+4FM+DQ得结果.
【详解】解:∵EF=a米,∠A=90°,∠AEF=30°,
∴AF=EF=a米,∠AFE=60°,
∵∠EFG=90°,
∴∠MFG=30°,
∴PQ=NP=MN=FM=(米),
DQ=QK cos30°=(米),
∴AD=AF+4FM+DQ=a+4×+=a+b(米),
故选:A.
【点睛】本题主要考查了矩形的性质,解直角三角形的应用,关键是通过解直角三角形求出AF、FM、DQ.
11.D
【分析】先利用斜坡的坡度求出,再利用矩形的性质和等腰三角形的性质求出,之后利用正切求出的值,最后通过求和即可得到建筑物BC的高度.
【详解】解:如图:过点D作于点F,过点E作于点G,过点E作于点H
∵斜坡的坡度
∴可设,
∵在中,,
∴
∵在中,
∵在中,
故选:D.
【点睛】本题考查坡度的意义,等腰直角三角形的性质和解直角三角形,选取恰当的方法正确求出线段长度是解题关键.
12.A
【详解】试题分析:连结AB,根据正切的定义得到tan∠A=,再根据圆周角定理得∠C=∠A,所以tan∠BCO=.
故选A.
考点:圆周角定理.
13.
【分析】先由非负性质得到△ABC中,tanA=1,cosB= ,求出∠A及∠B的度数,进而可得出结论.
【详解】解:∵△ABC中,|tanA-1|+(cosB-)2=0
∴tanA=1,cosB=
∴∠A=45°,∠B=60°,
∴∠C=75°.
故答案为75°.
【点睛】本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.
14.
【详解】解:∵梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,
∴,
∴AC=8m,
根据勾股定理,得
AB=m.
故答案为:
15.>
【分析】作一个含有48°的直角三角形,根据大角对大边可知,,再根据三角函数的定义有即可比较出大小.
【详解】解:作一个含有48°的直角三角形,如图,
∵,
∴,
∵
∴
故填:>.
【点睛】本题考查了三角函数的定义,解题关键是掌握三角函数的定义;在直角三角形中,任意一锐角的对边与斜边的比叫做的正弦,记作;在直角三角形中,任意一锐角的邻边与斜边的比叫做的余弦,记作.
16.
【详解】解:如图,过E作EF⊥CB于F,设菱形ABCD的边长为1.
∵DE∥AO,OB=3DB,
∴DE=AO=,
∴CE==,
∵△CDB是等边三角形,
∴∠DCF=60°,
∴∠CEF=30°,
∴CF=CE=,
∴EF=,BF==,
在Rt△EFB中,tan∠ABC==.
故答案为.
【点睛】本题考查锐角三角函数的定义;含30度角的直角三角形,熟练掌握相关知识点是解题的关键.
17. ; ;2.
【分析】根据三角函数的边角关系,列出关系式即可解题.
【详解】解:在Rt△ABC中,∠C=90°,BC:AC=1:2,
∴设BC=x,AC=2x,
∴AB=
∴sinA==, cosA==, tanB==2.
【点睛】本题考查了三角函数的表示,属于简单题,熟悉三角函数的定义并列出关系式是解题关键.
18.(1)图见解析
(2)图见解析
(3)图见解析
(4)图见解析,2
【分析】(1)根据旋转的性质即可将边BC绕点C逆时针旋转90°得到线段CD;
(2)根据网格即可在线段CD上找一点M,使得AM//BC;
(3)找到点D关于AC的对称点,连接交AC于点P,根据两点之间线段最短即可使DP+MP最小;
(4)依据(1)(2)(3)的作图,根据,可得∠BAC=a=45°,∠CAM=,利用三角形外角定义可得,进而可得.
【详解】(1)如图,线段CD即为所求,
(2)如图所示,点M即为所求,
(3)如图所示,点P即为所求,
(4)
∵,
∴,
∴,
∵,
∴
,
∵,
,
∴.
故答案为:2.
【点睛】本题考查了作图一旋转变换,平行线的性质,作图一轴对称变换,解直角三角形,解决本题的关键是掌握旋转的性质.
19.
【分析】本题根据直接代入法可以计算出题目所求.
【详解】把x=2+代入方程直接求得sinα= ,则cosα=,则tanα=.
【点睛】本题考查了三角函数与方程结合的知识,直接代入计算能力和解方程能力是解决此题的关键.
20.(1)答案见解析;(2).
【分析】(1)由四边形ABCD是矩形,EF⊥EC,易得∠A=∠D=90°,∠AFE=∠DEC,由有两组角对应相等的两个三角形相似,即可判定△AEF∽△DCE;
(2)由△AEF∽△DCE,根据相似三角形的对应边成比例,可得,又由矩形ABCD中,AB=2AD,E为AD的中点,tan∠ECF=,即可求得答案.
【详解】解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
∴△AEF∽△DCE;
(2)解:∵△AEF∽△DCE,
∴,
∵矩形ABCD中,AB=2AD,E为AD的中点,
∴DC=AB=2AD=4AE,
∴tan∠ECF==.
【点睛】此题考查了相似三角形的判定与性质、矩形的性质以及锐角三角函数的定义.此题难度适中,注意数形结合思想的应用.
21.(1)是等边三角形.
(2)海里
【分析】(1)根据图形和已知可得,,及 ,可证得是等边三角形;
(2)由图可求,然后可求 , ,由,再根据正弦定理可求解,然后根据乙船行驶的时间求出速度即可.
【详解】(1)解: 是等边三角形.理由如下:
根据题意得:,
,
,
又,
是等边三角形.
(2)解:是等边三角形,
,
根据题意得:,
.
,
在中,由正弦定理得:
∴乙船的速度的大小为(海里/小时).
答:乙船每小时航行海里.
22.14.
【分析】作PD⊥BC于点D,求出PB的长,在Rt△BPD中,利用三角函数求出PD的长;再在Rt△CPD中,求出PC的长.
【详解】如图,作PD⊥BC于点D,
根据题意, 得∠BPD=60°,∠CPD=45°,PB=AP-AB =20,
在Rt△BPD中,∴,
在Rt△CPD中,∴,
∴.
答:乙船的航行距离约是14海里.
23.
【分析】过A作,在中,因为,,得到,,在中,由,得到,从而得到,再结合垂直平分,得到,,在中,根据,得到,进而根据图形上线段关系得到.
【详解】过A作,垂足为点H,如图所示:
在中,,,
∴,,
在中,,
∴,
∴,
∵垂直平分,
∴,,
在中,,
∴,
∴.
【点睛】本题考查三角函数求线段长问题,涉及含角的直角三角形性质、正切函数、垂直平分线的性质、余弦函数等知识,熟练掌握三角函数求线段长是解决问题的关键.
24.乙船的航行速度约为每小时11海里.
【分析】设乙船的航行速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,则PC=2x海里,过P作PD⊥BC于D,求出BP,在Rt△BPD中求出PD,然后在Rt△PDC中表示出PD,继而建立方程可解出x的值.
【详解】设乙船的航行速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,则PC=2x海里,
过P作PD⊥BC于D,则BP=80﹣2×18=44(海里),
在Rt△PDB中,∠PDB=90°,∠BPD=60°,
∴PD=PB cos60°=22(海里),
在Rt△PDC中,∠PDC=90°,∠DPC=45°,
∴PD=PC cos45°=2x =x,
∴x=22,即x=11,
答:乙船的航行速度约为每小时11海里.
【点睛】本题考查了解直角三角形的应用﹣方向角问题,解答本题的关键是构造直角三角形,能利用三角函数表示相关线段的长度,难度一般.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
A. B. C.sin37° D.cos37°
2.的倒数为( )
A. B. C. D.
3.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为( ).
A. B. C. D.
4.如图,为的直径,弦交于点E,,则( )
A. B.1 C. D.2
5.如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
6.利用科学计算器计算,下列按键顺序正确的是( )
A.
B.
C.
D.
7.的值等于( )
A. B. C. D.
8.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
9.在平面直角坐标系中,直线与轴交于点,与轴交于点,将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接,则的长度为( )
A. B. C.2 D.
10.如图,在一块矩形ABCD区域内,正好划出5个全等的矩形停车位,其中EF=a米,FG=b米,∠AEF=30°,则AD等于( )
A.(a+b)米 B.(a+b)米
C.(a+b)米 D.(a+b)米
11.如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡行走100米至坡顶D处,再从D处沿水平方向继续前行若干米到点E处,在E点测得该建筑物顶端C的仰角为59°,建筑物底端B的俯角为,点A、B、C、D、E在同一平面内,斜坡的坡度 .根据以上数据,计算出建筑物BC的高度约为(结果精确到1.参考数据:,,)( )
A.158米 B.161米 C.159米 D.160米
12.如图,经过原点的⊙P与两坐标轴分别交于点A(2,0)和点B(0,2), C是优弧上的任意一点(不与点O,B重合),则tan∠BCO的值为( )
A. B. C. D.
二、填空题
13.在锐角中,如果,满足,那么 .
14.如图,已知梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,则斜坡AB的长为 m.
15.比较大小:sin48° cos48°(填“>”、“<”或“=”).
16.如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是 .
17.如图,在△ABC中,∠C=90°,BC:AC=1:2,则sinA= ,cosA= ,tanB= .
三、解答题
18.如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点,△ABC的三个顶点在格点上,仅用无刻度的直尺在网格中画图,画图过程用虚线表示.
(1)将边BC绕点C逆时针旋转90°得到线段CD;
(2)在线段CD上找一点M,使得AMBC;
(3)在AC上找一点P,使DP+MP最小;
(4)依据(1)(2)(3)的作图,试探究:若α、β是锐角,且tanα=1,tanβ=,则tan(α+β)= .
19.已知2+是方程x2-5xsinα+1=0的一个根,α为锐角,求tanα的值.
20.如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
21.在一个三角形中,各边和它所对角的正弦的比相等.即.利用上述结论可以求解如下题目.如:
在中,若,,,求.
解:在中,
问题解决:
如图,甲船以每小时海里的速度向正北方航行,当甲船位于处时,乙船位于甲船的北偏西方向的处,且乙船从处按北偏东方向匀速直线航行,当甲船航行分钟到达处时,乙船航行到甲船的北偏西方向的处,此时两船相距海里.
(1)判断的形状,并给出证明.
(2)乙船每小时航行多少海里?
22.如图,甲船在港口P的南偏东60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度驶向港口P;乙船从港口P出发,沿南偏西45°方向驶离港口P.现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向,求乙船的航行距离.(,,结果保留整数).
23.如图,已知中,,,,边的垂直平分线分别交、于点、.求线段的长.
24.如图,甲船在港口P的南偏西60°方向,距港口80海里的A处,沿AP方向以每小时18海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,已知两船同时出发,经过2小时乙船恰好在甲船的正东方向.求乙船的行驶速度.(结果保留根号)
《第一章解直角三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B A A A B A
题号 11 12
答案 D A
1.B
【分析】过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CDAC=40海里,再解Rt△CBD中,得出BC海里,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.
【详解】如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80,∴CDAC=40.
在Rt△CBD中,∵∠CDB=90°,∠BCD=37°,∴BC,∴海警船到大事故船C处所需的时间大约为:40(小时).
故选B.
【点睛】本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.
2.A
【分析】根据特殊角的三角函数值以及倒数的定义即可求解.
【详解】解:,的倒数是
∴的倒数为,
故选:A.
【点睛】本题考查了特殊角的三角函数值以及倒数的定义,熟练掌握特殊角的三角函数值以及倒数的定义是解题的关键.
3.A
【分析】
在中,,由此可以求出之长.
【详解】
解:在中,
,
.
又,,
.
故选:.
【点睛】此题考查了正切的概念和运用,关键是把实际问题转化成数学问题,把它抽象到直角三角形中来.
4.B
【分析】根据为的直径,可证出,再根据已知和三角函数即可得出和,进而即可得解.
【详解】解:∵为的直径,,
∴,
∴,
∵,
∴,
∵为的直径,
∴,
∴,
∴,
∴.
故选:B.
【点睛】本题考查的是圆周角定理的应用,垂径定理推论的应用,锐角三角函数的应用,熟练的运用锐角三角函数求解的长是解本题的关键.
5.B
【详解】解:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,
根据勾股定理的逆定理可知∠ABC=90°,
根据平行线的性质可得:∠ABE=110°,
则∠CBE=110°-90°=20°,
即点C在点B的北偏西20°方向上.
故选B
6.A
【分析】简单的电子计算器工作顺序是先输入者先算,根据按键顺序写出式子,再根据开方运算即可求出显示的结果.
【详解】
解:利用该型号计算器计算 ,按键顺序正确的是:
故选:A.
【点睛】本题主要考查了计算器-三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
7.A
【详解】3cos60°=3×=.
故选A.
点睛:熟记特殊角的三角函数值.
8.A
【分析】根据锐角A的邻边a与对边b的比叫做∠A的余切,记作cotA.
【详解】解:∵∠C=90°,
∴=,
故选:A.
【点睛】此题主要考查了锐角三角函数的定义,关键是掌握余切定义.
9.B
【分析】先求出点A、B的坐标,可求得OA、OB,进而可求得∠OAB=60°,利用旋转的性质和等边三角形的判定与性质证明和为等边三角形得到即可求解.
【详解】解:对于,
当时,,当时,由得:,
则A(1,0),B(0,),
∴,,
∴,则∠OAB=60°,
由旋转性质得:,,,
∴是等边三角形,
∴,又
∴是等边三角形,
∴,
故选:B.
【点睛】本题考查一次函数图象与坐标轴的交点问题、旋转性质、等边三角形的判定与性质、解直角三角形,熟练掌握相关知识的联系与运用,证得是等边三角形是解答的关键.
10.A
【分析】在Rt△AEF中,通过解直角三角形求得AF,再在Rt△FMG和Rt△DQK中,通过解直角三角形求得FM,最后由AD=AF+4FM+DQ得结果.
【详解】解:∵EF=a米,∠A=90°,∠AEF=30°,
∴AF=EF=a米,∠AFE=60°,
∵∠EFG=90°,
∴∠MFG=30°,
∴PQ=NP=MN=FM=(米),
DQ=QK cos30°=(米),
∴AD=AF+4FM+DQ=a+4×+=a+b(米),
故选:A.
【点睛】本题主要考查了矩形的性质,解直角三角形的应用,关键是通过解直角三角形求出AF、FM、DQ.
11.D
【分析】先利用斜坡的坡度求出,再利用矩形的性质和等腰三角形的性质求出,之后利用正切求出的值,最后通过求和即可得到建筑物BC的高度.
【详解】解:如图:过点D作于点F,过点E作于点G,过点E作于点H
∵斜坡的坡度
∴可设,
∵在中,,
∴
∵在中,
∵在中,
故选:D.
【点睛】本题考查坡度的意义,等腰直角三角形的性质和解直角三角形,选取恰当的方法正确求出线段长度是解题关键.
12.A
【详解】试题分析:连结AB,根据正切的定义得到tan∠A=,再根据圆周角定理得∠C=∠A,所以tan∠BCO=.
故选A.
考点:圆周角定理.
13.
【分析】先由非负性质得到△ABC中,tanA=1,cosB= ,求出∠A及∠B的度数,进而可得出结论.
【详解】解:∵△ABC中,|tanA-1|+(cosB-)2=0
∴tanA=1,cosB=
∴∠A=45°,∠B=60°,
∴∠C=75°.
故答案为75°.
【点睛】本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.
14.
【详解】解:∵梯形护坡坝AB的坡度为i=1:4,坡高BC=2m,
∴,
∴AC=8m,
根据勾股定理,得
AB=m.
故答案为:
15.>
【分析】作一个含有48°的直角三角形,根据大角对大边可知,,再根据三角函数的定义有即可比较出大小.
【详解】解:作一个含有48°的直角三角形,如图,
∵,
∴,
∵
∴
故填:>.
【点睛】本题考查了三角函数的定义,解题关键是掌握三角函数的定义;在直角三角形中,任意一锐角的对边与斜边的比叫做的正弦,记作;在直角三角形中,任意一锐角的邻边与斜边的比叫做的余弦,记作.
16.
【详解】解:如图,过E作EF⊥CB于F,设菱形ABCD的边长为1.
∵DE∥AO,OB=3DB,
∴DE=AO=,
∴CE==,
∵△CDB是等边三角形,
∴∠DCF=60°,
∴∠CEF=30°,
∴CF=CE=,
∴EF=,BF==,
在Rt△EFB中,tan∠ABC==.
故答案为.
【点睛】本题考查锐角三角函数的定义;含30度角的直角三角形,熟练掌握相关知识点是解题的关键.
17. ; ;2.
【分析】根据三角函数的边角关系,列出关系式即可解题.
【详解】解:在Rt△ABC中,∠C=90°,BC:AC=1:2,
∴设BC=x,AC=2x,
∴AB=
∴sinA==, cosA==, tanB==2.
【点睛】本题考查了三角函数的表示,属于简单题,熟悉三角函数的定义并列出关系式是解题关键.
18.(1)图见解析
(2)图见解析
(3)图见解析
(4)图见解析,2
【分析】(1)根据旋转的性质即可将边BC绕点C逆时针旋转90°得到线段CD;
(2)根据网格即可在线段CD上找一点M,使得AM//BC;
(3)找到点D关于AC的对称点,连接交AC于点P,根据两点之间线段最短即可使DP+MP最小;
(4)依据(1)(2)(3)的作图,根据,可得∠BAC=a=45°,∠CAM=,利用三角形外角定义可得,进而可得.
【详解】(1)如图,线段CD即为所求,
(2)如图所示,点M即为所求,
(3)如图所示,点P即为所求,
(4)
∵,
∴,
∴,
∵,
∴
,
∵,
,
∴.
故答案为:2.
【点睛】本题考查了作图一旋转变换,平行线的性质,作图一轴对称变换,解直角三角形,解决本题的关键是掌握旋转的性质.
19.
【分析】本题根据直接代入法可以计算出题目所求.
【详解】把x=2+代入方程直接求得sinα= ,则cosα=,则tanα=.
【点睛】本题考查了三角函数与方程结合的知识,直接代入计算能力和解方程能力是解决此题的关键.
20.(1)答案见解析;(2).
【分析】(1)由四边形ABCD是矩形,EF⊥EC,易得∠A=∠D=90°,∠AFE=∠DEC,由有两组角对应相等的两个三角形相似,即可判定△AEF∽△DCE;
(2)由△AEF∽△DCE,根据相似三角形的对应边成比例,可得,又由矩形ABCD中,AB=2AD,E为AD的中点,tan∠ECF=,即可求得答案.
【详解】解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
∴△AEF∽△DCE;
(2)解:∵△AEF∽△DCE,
∴,
∵矩形ABCD中,AB=2AD,E为AD的中点,
∴DC=AB=2AD=4AE,
∴tan∠ECF==.
【点睛】此题考查了相似三角形的判定与性质、矩形的性质以及锐角三角函数的定义.此题难度适中,注意数形结合思想的应用.
21.(1)是等边三角形.
(2)海里
【分析】(1)根据图形和已知可得,,及 ,可证得是等边三角形;
(2)由图可求,然后可求 , ,由,再根据正弦定理可求解,然后根据乙船行驶的时间求出速度即可.
【详解】(1)解: 是等边三角形.理由如下:
根据题意得:,
,
,
又,
是等边三角形.
(2)解:是等边三角形,
,
根据题意得:,
.
,
在中,由正弦定理得:
∴乙船的速度的大小为(海里/小时).
答:乙船每小时航行海里.
22.14.
【分析】作PD⊥BC于点D,求出PB的长,在Rt△BPD中,利用三角函数求出PD的长;再在Rt△CPD中,求出PC的长.
【详解】如图,作PD⊥BC于点D,
根据题意, 得∠BPD=60°,∠CPD=45°,PB=AP-AB =20,
在Rt△BPD中,∴,
在Rt△CPD中,∴,
∴.
答:乙船的航行距离约是14海里.
23.
【分析】过A作,在中,因为,,得到,,在中,由,得到,从而得到,再结合垂直平分,得到,,在中,根据,得到,进而根据图形上线段关系得到.
【详解】过A作,垂足为点H,如图所示:
在中,,,
∴,,
在中,,
∴,
∴,
∵垂直平分,
∴,,
在中,,
∴,
∴.
【点睛】本题考查三角函数求线段长问题,涉及含角的直角三角形性质、正切函数、垂直平分线的性质、余弦函数等知识,熟练掌握三角函数求线段长是解决问题的关键.
24.乙船的航行速度约为每小时11海里.
【分析】设乙船的航行速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,则PC=2x海里,过P作PD⊥BC于D,求出BP,在Rt△BPD中求出PD,然后在Rt△PDC中表示出PD,继而建立方程可解出x的值.
【详解】设乙船的航行速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,则PC=2x海里,
过P作PD⊥BC于D,则BP=80﹣2×18=44(海里),
在Rt△PDB中,∠PDB=90°,∠BPD=60°,
∴PD=PB cos60°=22(海里),
在Rt△PDC中,∠PDC=90°,∠DPC=45°,
∴PD=PC cos45°=2x =x,
∴x=22,即x=11,
答:乙船的航行速度约为每小时11海里.
【点睛】本题考查了解直角三角形的应用﹣方向角问题,解答本题的关键是构造直角三角形,能利用三角函数表示相关线段的长度,难度一般.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
