2.2切线长定理同步练习(含解析)
图片预览



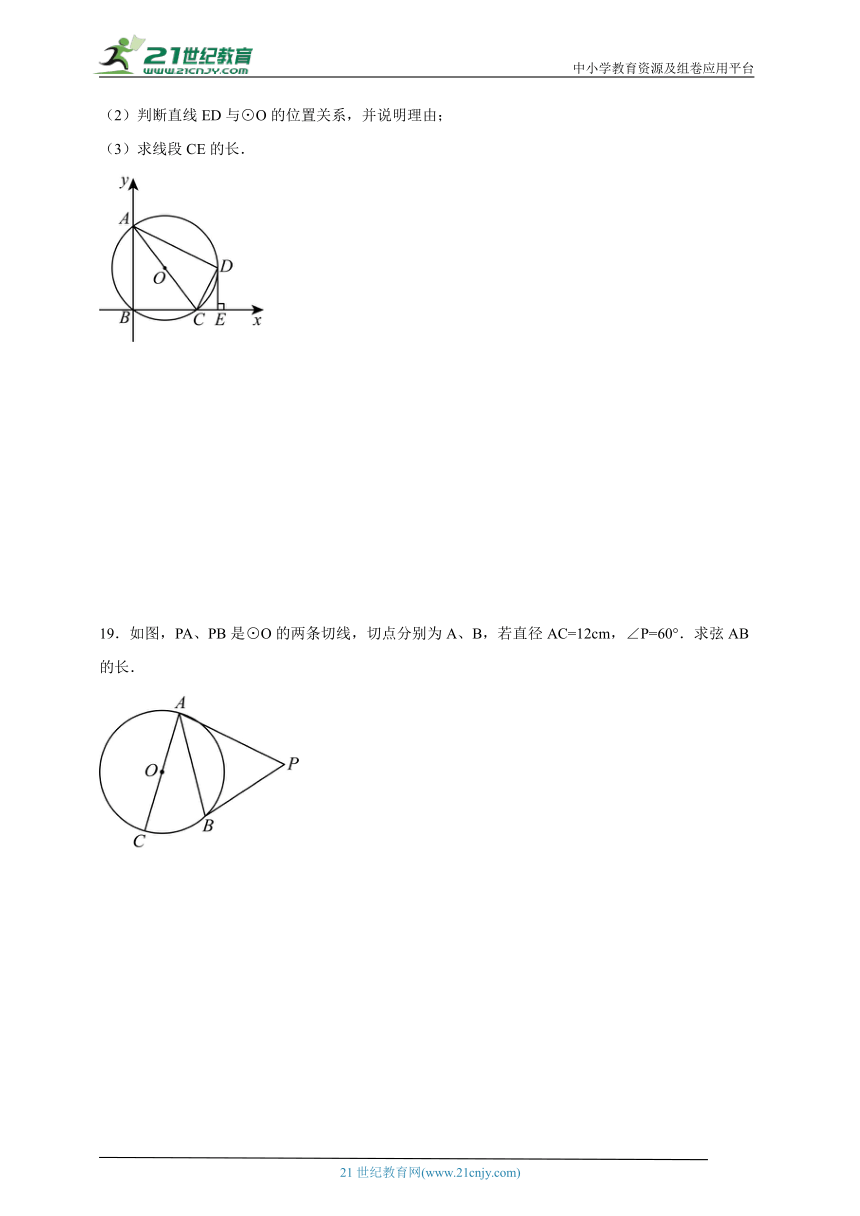
文档简介
中小学教育资源及组卷应用平台
2.2切线长定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,P为外一点,分别切于点A、B,切于点E,分别交于点C、D,若,则的周长为( )
A.8 B.12 C.16 D.20
2.如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且ABDC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( )
A.4 B.3
C.2 D.1
3.如图,的半径为2,,是的两条切线,切点分别为A,B.连接,,,,若,则的周长为( )
A. B. C.6 D.3
4.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.=PC PO
5.圆O内切于三角形,在斜边上的切点为D,,,则内切圆的半径为( )
A.2 B.3 C.4 D.5
6.如图,切于,切于,交于,连接,下列结论中,错误的是( ).
A. B. C. D.以上都不对
7.如图,从圆外一点引圆的两条切线,,切点分别为,,如果, ,那么弦AB的长是( )
A. B. C. D.
8.如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D.下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图所示,为外一点,、分别切于、,切于点,分别交、于点、,若,则的周长为( )
A.15 B.12 C.20 D.30
10.如图,与的两边分别相切,其中OA边与⊙C相切于点P.若,,则OC的长为( )
A.8 B. C. D.
11.如图,P为圆O外一点,分别切圆O于两点,若,则( ).
A.2 B.3 C.4 D.5
12.如图,△ABC的内切圆⊙O分别与AB,BC,AC相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
二、填空题
13.等腰直角△ABC中, ∠C=90度,斜边AB=6,则此三角形的内心与外心之间的距离是 .
14.如图,PA、PB是⊙O的切线,切点为A、B,若OP=4,PA=2,则∠AOB的度数为 .
15.如图,直线,,分别与相切于,,,且,若,,则的长等于 .
16.如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有 个.
17.如图,四边形是的外切四边形,且,,则四边形的周长为 .
三、解答题
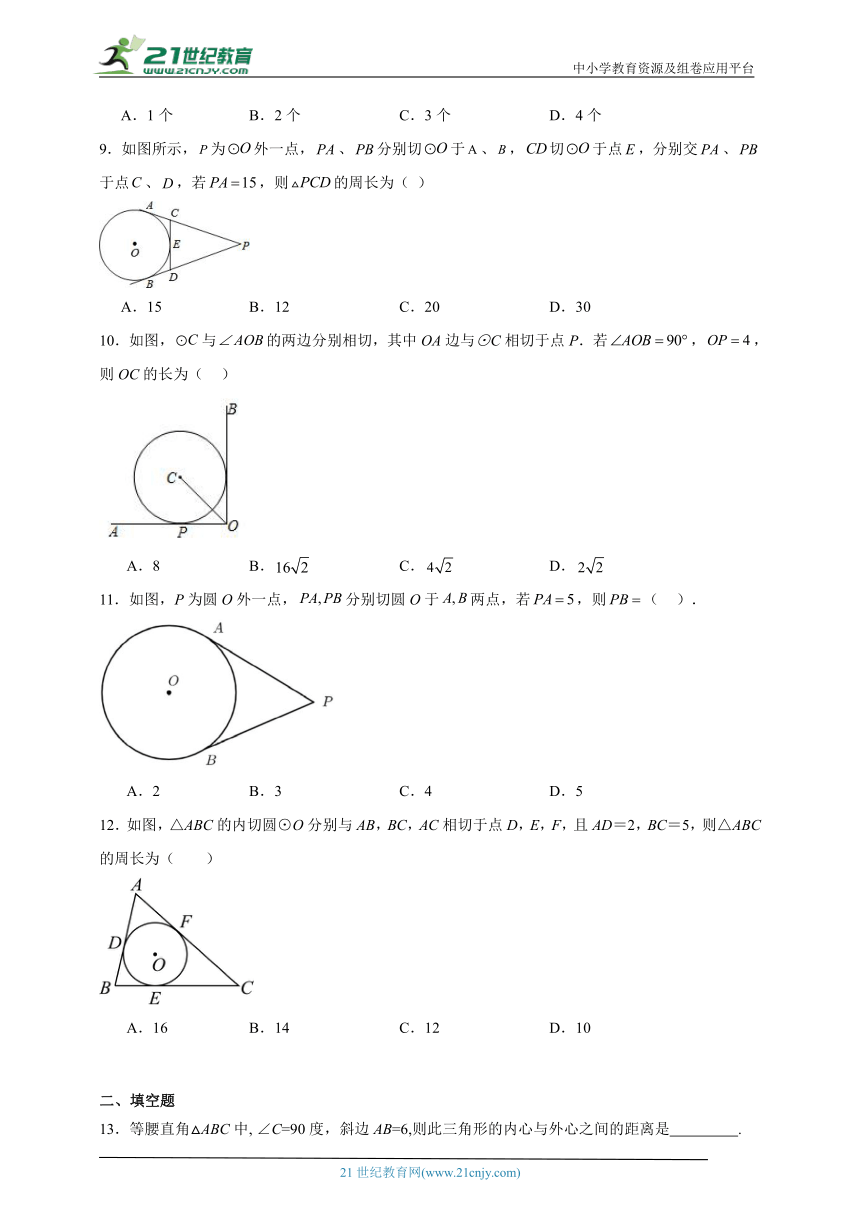
18.如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且,过点D作DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)求线段CE的长.
19.如图,PA、PB是⊙O的两条切线,切点分别为A、B,若直径AC=12cm,∠P=60°.求弦AB的长.
20.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出.这张光盘的直径是多少?
21.已知:如图,在△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
22.如图,是⊙O的切线,A,B为切点,是⊙O的直径,,求和的度数.
23.如图,直线分别与⊙O相切于点,且.求:
(1)的度数;
(2)⊙O的半径.
24.如图,⊙O是GDP的内切圆,切点分别为A、B、H,切线EF与⊙O相切于点C,分别交PA、PB于点E、F.
(1)若△PEF的周长为12,求线段PA的长;
(2)若∠G=90°,GD=3,GP=4,求⊙O半径.
《2.2切线长定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D A D C D D C
题号 11 12
答案 D B
1.C
【分析】根据切线长定理得到 , , ,再根据三角形的周长公式计算即可.
【详解】解: 分别切 于点 , 切 于点 ,,
, , ,
的周长
,
故选:C .
【点睛】本题考查了切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,关键是把的周长转化为已知切线相关的线段计算.
2.A
【分析】连结OF,①②利用切线长定理即可判断正确性,③先推导∠OEB=∠OFB=∠OFC=∠OGC=90 ,再证∠EBO=∠FBO,∠FCO=∠GCO,可证△BEO≌△BFO(AAS),△FCO≌△GCO(AAS),可推出∠FOB+∠FOC=90 ,即∠BOC=90°③正确;④由△OBC、△BEO、△CGO都是直角三角形,再证∠GOC=∠EBO=∠OBC,可得△BEO∽△BOC∽△OGC④正确.
【详解】连结OF,
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
又因为CG与CF为切线长,BE与BF也为切线长,
∴CG=CF,BE=BF,
∴①CG=CF,②BE=BF正确;
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
∴OE⊥AB,OF⊥BC,OG⊥CD,
∴∠OEB=∠OFB=∠OFC=∠OGC=90 ,
∴OB平分∠EBF,OC平分∠FCG,
∴∠EBO=∠FBO,∠FCO=∠GCO,
∴△BEO≌△BFO(AAS),△FCO≌△GCO(AAS),
∴∠EOB=∠FOB,∠FOC=∠GOC,
∵∠EOB+∠FOB+∠FOC+∠GOC=180 ,
∴2∠FOB+2∠FOC=180 ,
∴∠FOB+∠FOC=90 ,
∴∠BOC=∠FOB+∠FOC=90 ,
∴③∠BOC=90°正确;;
由△OBC、△BEO、△CGO都是直角三角形,
∵∠EOB+∠EBO=90 ,∠EOB+∠EBO=90 ,
∴∠GOC=∠EBO=∠OBC,
△BEO∽△BOC∽△OGC,
∴④△BEO~△BOC~△OGC正确,
①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数有4个,
故选择:A.
【点睛】本题考查切线的性质,三角形全等,三角形相似,掌握切线的性质,三角形全等的证明方法与性质,三角形相似的判定定理与判定方法的选择是解题关键.
3.A
【分析】由切线的性质可得出,由切线长定理可得出,从而可判断为等边三角形,又易证,即可求出,从而可求出,进而可求出,最后由三角形周长公式求解即可.
【详解】解:∵,是的两条切线,切点分别为A,B,
∴,.
∵,
∴为等边三角形,
∴.
∵,
∴,
∴,
∴,
∴,
∴的周长为.
故选A.
【点睛】本题考查切线的性质,切线长定理,等边三角形的判定和性质,三角形全等的判定和性质.掌握从圆外一点引圆的两条切线,它们的切线长相等是解题关键.
4.D
【详解】连接OA、OB,AB,
∵PA切⊙O于A,PB切⊙O于B,
由切线长定理知,∠1=∠2,PA=PB,
∴△ABP是等腰三角形,
∵∠1=∠2,
∴AB⊥OP(等腰三角形三线合一),
故A,B,C正确,
根据切割线定理知:=PC (PO+OC),因此D错误.
故选D.
5.A
【分析】先证得四边形为正方形;再设的半径为r,由勾股定理得,解此方程即可求得答案.
【详解】解:由题意得,是直角三角形,且,设内切圆与三边分别切于点D,E,F,连接,,如图,
∵是的内切圆,
∴,,
∴,
∵,
∴四边形为矩形,
∵,
∴矩形为正方形;
设的半径为r,
∵四边形为正方形,
∴,
∵是的内切圆,
∴,,
∴,,,
在中,,
∴,
解得:(舍去),
∴的半径为2;
故选:A.
【点睛】此题考查了三角形的内切圆的性质、切线长定理、正方形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.
6.D
【分析】连接,,根据切线长定理可得,再证明,问题得解.
【详解】连接,,如图,
∵切于,切于,
∴,即是等腰三角形,
∵,,
∴,
∴,即平分,
∴,即A、B、C三项都正确,
故选:D.
【点睛】本题主要考查了切线长定理,等腰三角形的判定与性质,全等三角形的判定与性质等知识,掌握切线长定理,是解答本题的关键.
7.C
【分析】先利用切线长定理得到,再利用可判断为等边三角形,然后根据等边三角形的性质求解.
【详解】解:,PB为的切线,
,
,
为等边三角形,
.
故选C.
【点睛】本题考查切线长定理,掌握切线长定理是解题的关键.
8.D
【详解】根据切线长定理可知PA=PB,故①正确;
同理可知CA=CE,可知CO为∠ACE的角平分线,所以∠ACO=∠DCO,故②正确;
同理可知DE=BD,由切线的性质可知∠OBD=∠OED=90°,可根据四边形的内角和为360°知∠BOE+∠BDE=180°,即∠BOE和∠BDE互补,故③正确;
根据切线长定理可得CE=CA,BD=DE,而△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+AC+PD+DB=PA+PB=2PB,故④正确.
故选D.
9.D
【分析】直接利用切线长定理得出AC=EC,BD=DE,AP=BP,进而求出答案.
【详解】∵P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,
∴AC=EC,BD=DE,AP=BP,
∵PA=15,∴△PCD的周长为:PA+PB=30.
故选D.
【点睛】此题主要考查了切线长定理,得出△PCD的周长为:PA+PB是解题关键.
10.C
【分析】如图所示,连接CP,由切线的性质和切线长定理得到∠CPO=90°,∠COP=45°,由此推出CP=OP=4,再根据勾股定理求解即可.
【详解】解:如图所示,连接CP,
∵OA,OB都是圆C的切线,∠AOB=90°,P为切点,
∴∠CPO=90°,∠COP=45°,
∴∠PCO=∠COP=45°,
∴CP=OP=4,
∴,
故选C.
【点睛】本题主要考查了切线的性质,切线长定理,等腰直角三角形的性质与判定,勾股定理,熟知切线长定理是解题的关键.
11.D
【分析】根据切线长定理直接求得PB=PA=5.
【详解】∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故选:D.
【点睛】本题考查了切线长定理,熟练掌握切线长定理是解题的关键.
12.B
【分析】根据切线长定理得到AF=AD=2,BD=BE,CE=CF,根据BC=5即可得到△ABC的周长.
【详解】解:∵△ABC的内切圆⊙O分别与AB,BC,AC相切于点D,E,F,且AD=2,
∴AF=AD=2,BD=BE,CE=CF,
∵BE+CE=BC=5,
∴BD+CF=BE+CE =BC=5,
∴△ABC的周长=2+2+5+5=14,
故选:B.
【点睛】本题考查切线长定理,熟练掌握切线长定理是解题的关键.
13.3
【分析】运用等腰直角三角形的性质和内心、外心的定义来解答,首先根据面积求出内切圆的半径,再利用勾股定理求出外接圆的半径,最后求解.
【详解】如图,∵AB=6,AC=BC,∠ABC=90°
∴CO1= AO1= BO1=3
AC=BC=
∵O2是内心,
∴
∴r=3-3
即O1O2=3-3
故答案为3-3
【点睛】此题主要考查了三角形的内心和外心,掌握等腰直角三角形的性质和三角形内切圆的半径的求法是解题关键.
14.120°
【解析】略
15.10cm
【分析】根据平行线的性质以及切线长定理,即可证明,再根据勾股定理即可求得的长,再结合切线长定理即可求解.
【详解】解: ,
,
、,分别与相切于、、,
,,,,
,
,
,
.
故答案为:10cm.
【点睛】此题主要是考查了切线长定理.从圆外一点引圆的两条切线,它们的切线长相等,且圆心和这点的连线平分两条切线的夹角.
16.2
【分析】根据切线长定理,可判断①正确;将的周长转化为,可判断②错误;连接、、,求出,再由,可判断③正确.
【详解】解:、是的切线,
,故①正确;
、、是的切线,
,,
的周长,故②错误;
连接、、,
,
,故③正确.
综上可得①③正确,共2个.
故选:.
【点睛】本题考查了切线的性质及切线长定理,熟悉相关性质是解答本题的关键.
17.48
【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=24,根据四边形的周长公式计算,得到答案.
【详解】解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=24,
∴四边形ABCD的周长=AD+BC+AB+CD=24+24=48,
故答案为:48.
【点睛】本题考查了切线长定理,掌握从圆外一点引圆的两条切线,它们的切线长相等是解题的关键.
18.(1)见解析;(2)直线ED与⊙O相切,理由见解析;(3)2
【分析】(1)说明∠DCE=∠DAB, ∠DAB=∠ACD,从而说明CD平分∠ACE;(2)连接OD,利用∠EDC+∠DCE=90°,∠DCE=∠ACD=∠ODC,从而∠EDC+∠ODC=90°;(3)延长DO交AB于点H,求出BD的长,即BE的长,CE=BE-BC.
【详解】(1)∵四边形ABCD是⊙O内接四边形,∴∠BAD+∠BCD=180°,
又∵∠BCD+∠DCE=180°, ∴∠DCE=∠BAD,
∵=, ∴∠BAD=∠ACD,
∴∠DCE=∠ACD, ∴CD平分∠ACE.
(2)直线ED与⊙O相切.连接OD.
∵OC=OD,∴∠ODC=∠OCD,
又∵∠DCE=∠ACD,∴∠DCE=∠ODC,
∴OD∥BE,∴∠ODE=∠DEC,
又∵DE⊥BC,∴∠DEC=90°,
∴∠ODE=90° ∴OD⊥DE,
∴ED与⊙O相切.
(3)延长DO交AB于点H.
∵OD∥BE,O是AC的中点,
∴H是AB的中点,
∴HO是△ABC的中位线,
∴HO=BC=3,
又∵AC为直径, ∴∠ADC=90°,
又∵O是AC的中点
∴OD=AC=×=5,
∴HD=3+5=8,
∵∠ABC=∠DEC=∠ODE=90°,
∴四边形BEDH是矩形,
∴BE=HD=8,
∴CE=8﹣6=2.
【点睛】此题考查了圆的综合题,涉及的知识有:坐标与图形性质,勾股定理,以及圆周角性质、矩形的判定.
19.6
【分析】连接CB.由切线长定理知PA=PB;又∠P=60°,则等腰三角形APB是等边三角形,则有ABP=60°;由弦切角定理知,∠PAB=∠C=60°,AC是直径;由直径对的圆周角是直角得∠ABC=90°,则在Rt△ABC中,有∠CAB=30°,进而可得结论.
【详解】连接CB.
∵PA、PB是⊙O的切线,∴PA=PB,
又∵∠P=60°,∴∠PAB=60°;
又∵AC是⊙O的直径,∴CA⊥PA,∠ABC=90°,∴∠CAB=30°,
而AC=12,∴在Rt△ABC中,cos30°=,∴AB=12×=6.
【点睛】本题考查了切线长定理,等边三角形的判定和性质,弦切角定理,直角三角形的性质.注意本题的解法不唯一.
20.
【分析】设光盘的圆心为O,光盘与三角尺的切点为C,连接.则,,进而根据切线长定理,可得,证明,从而得到,在中,解直角三角形即可求得,进而求得光盘的直径.
【详解】如图,设光盘的圆心为O,光盘与三角尺的切点为C,连接,则,,
是的切线
,
在中,.
的直径为.
答:这张光盘的直径是.
【点睛】本题考查了切线长定理,解直角三角形,掌握切线长定理是解题的关键.
21.(1)证明见解析;(2)证明见解析.
【详解】(1)证明:∵∠ABC=90°,
∴OB⊥BC
∵OB是⊙O的半径,
∴CB为⊙O的切线.
又∵CD切⊙O于点D,
∴BC=CD;
(2)证明:∵BE是⊙O的直径,
∴∠BDE=90°.
∴∠ADE+∠CDB=90°.
又∵∠ABC=90°,
∴∠ABD+∠CBD=90°.
由(1)得BC=CD,
∴∠CDB=∠CBD
∴∠ADE=∠ABD;
考点:切线的判定与性质.
22.,
【分析】根据切线的性质,得到,利用互余关系求出的度数,利用切线长定理,得到是等腰三角形,利用三角形内角和求出的度数即可.
【详解】解:∵是⊙O的切线,
∴,
∴,
∴,
∴.
【点睛】本题考查切线的性质和切线长定理.熟练掌握切线的性质和切线长定理是解题的关键.
23.(1)90°;(2)
【分析】(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;
(2)由勾股定理可求得BC的长,再根据三角形的面积,即可求得半径.
【详解】解:(1)连接OF;
根据切线长定理得:BE=BF,CF=CG,
∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°;
(2)∵OB=6cm,OC=8cm,
∴BC=10cm,
故半径为:4.8.
【点睛】此题主要是综合运用了切线长定理和切线的性质定理.由勾股定理可求得BC的长是关键.
24.(1)6;(2)1
【分析】(1)由切线长定理可得,,,再由△PEF的周长为12,即可得到,由此即可得到答案;
(2)连接OA、OB、OH、OP、OD、OG,设圆的半径为r,由,可以得到,再利用勾股定理求出,由此进行求解即可.
【详解】解:(1)由题意得,AP,BP,EF都是圆O的切线,
∴由切线长定理可得,,,
∵△PEF的周长为12,
∴,
∴;
(2)如图所示,连接OA、OB、OH、OP、OD、OG,设圆的半径为r,
∴OA=OB=OH=r,
由切线的性质可得OA⊥PD,OB⊥PG,OH⊥DG,
∴
,
∵∠G=90°,GD=3,GP=4,
∴,,
∴即,
∴,
∴⊙O的半径为1.
【点睛】本题主要考查了切线长定理,切线的性质,勾股定理,解题的关键在于能够熟练掌握切线长定理和切线的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.2切线长定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,P为外一点,分别切于点A、B,切于点E,分别交于点C、D,若,则的周长为( )
A.8 B.12 C.16 D.20
2.如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且ABDC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( )
A.4 B.3
C.2 D.1
3.如图,的半径为2,,是的两条切线,切点分别为A,B.连接,,,,若,则的周长为( )
A. B. C.6 D.3
4.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.=PC PO
5.圆O内切于三角形,在斜边上的切点为D,,,则内切圆的半径为( )
A.2 B.3 C.4 D.5
6.如图,切于,切于,交于,连接,下列结论中,错误的是( ).
A. B. C. D.以上都不对
7.如图,从圆外一点引圆的两条切线,,切点分别为,,如果, ,那么弦AB的长是( )
A. B. C. D.
8.如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D.下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图所示,为外一点,、分别切于、,切于点,分别交、于点、,若,则的周长为( )
A.15 B.12 C.20 D.30
10.如图,与的两边分别相切,其中OA边与⊙C相切于点P.若,,则OC的长为( )
A.8 B. C. D.
11.如图,P为圆O外一点,分别切圆O于两点,若,则( ).
A.2 B.3 C.4 D.5
12.如图,△ABC的内切圆⊙O分别与AB,BC,AC相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
二、填空题
13.等腰直角△ABC中, ∠C=90度,斜边AB=6,则此三角形的内心与外心之间的距离是 .
14.如图,PA、PB是⊙O的切线,切点为A、B,若OP=4,PA=2,则∠AOB的度数为 .
15.如图,直线,,分别与相切于,,,且,若,,则的长等于 .
16.如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有 个.
17.如图,四边形是的外切四边形,且,,则四边形的周长为 .
三、解答题
18.如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且,过点D作DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)求线段CE的长.
19.如图,PA、PB是⊙O的两条切线,切点分别为A、B,若直径AC=12cm,∠P=60°.求弦AB的长.
20.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出.这张光盘的直径是多少?
21.已知:如图,在△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
22.如图,是⊙O的切线,A,B为切点,是⊙O的直径,,求和的度数.
23.如图,直线分别与⊙O相切于点,且.求:
(1)的度数;
(2)⊙O的半径.
24.如图,⊙O是GDP的内切圆,切点分别为A、B、H,切线EF与⊙O相切于点C,分别交PA、PB于点E、F.
(1)若△PEF的周长为12,求线段PA的长;
(2)若∠G=90°,GD=3,GP=4,求⊙O半径.
《2.2切线长定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D A D C D D C
题号 11 12
答案 D B
1.C
【分析】根据切线长定理得到 , , ,再根据三角形的周长公式计算即可.
【详解】解: 分别切 于点 , 切 于点 ,,
, , ,
的周长
,
故选:C .
【点睛】本题考查了切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,关键是把的周长转化为已知切线相关的线段计算.
2.A
【分析】连结OF,①②利用切线长定理即可判断正确性,③先推导∠OEB=∠OFB=∠OFC=∠OGC=90 ,再证∠EBO=∠FBO,∠FCO=∠GCO,可证△BEO≌△BFO(AAS),△FCO≌△GCO(AAS),可推出∠FOB+∠FOC=90 ,即∠BOC=90°③正确;④由△OBC、△BEO、△CGO都是直角三角形,再证∠GOC=∠EBO=∠OBC,可得△BEO∽△BOC∽△OGC④正确.
【详解】连结OF,
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
又因为CG与CF为切线长,BE与BF也为切线长,
∴CG=CF,BE=BF,
∴①CG=CF,②BE=BF正确;
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
∴OE⊥AB,OF⊥BC,OG⊥CD,
∴∠OEB=∠OFB=∠OFC=∠OGC=90 ,
∴OB平分∠EBF,OC平分∠FCG,
∴∠EBO=∠FBO,∠FCO=∠GCO,
∴△BEO≌△BFO(AAS),△FCO≌△GCO(AAS),
∴∠EOB=∠FOB,∠FOC=∠GOC,
∵∠EOB+∠FOB+∠FOC+∠GOC=180 ,
∴2∠FOB+2∠FOC=180 ,
∴∠FOB+∠FOC=90 ,
∴∠BOC=∠FOB+∠FOC=90 ,
∴③∠BOC=90°正确;;
由△OBC、△BEO、△CGO都是直角三角形,
∵∠EOB+∠EBO=90 ,∠EOB+∠EBO=90 ,
∴∠GOC=∠EBO=∠OBC,
△BEO∽△BOC∽△OGC,
∴④△BEO~△BOC~△OGC正确,
①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数有4个,
故选择:A.
【点睛】本题考查切线的性质,三角形全等,三角形相似,掌握切线的性质,三角形全等的证明方法与性质,三角形相似的判定定理与判定方法的选择是解题关键.
3.A
【分析】由切线的性质可得出,由切线长定理可得出,从而可判断为等边三角形,又易证,即可求出,从而可求出,进而可求出,最后由三角形周长公式求解即可.
【详解】解:∵,是的两条切线,切点分别为A,B,
∴,.
∵,
∴为等边三角形,
∴.
∵,
∴,
∴,
∴,
∴,
∴的周长为.
故选A.
【点睛】本题考查切线的性质,切线长定理,等边三角形的判定和性质,三角形全等的判定和性质.掌握从圆外一点引圆的两条切线,它们的切线长相等是解题关键.
4.D
【详解】连接OA、OB,AB,
∵PA切⊙O于A,PB切⊙O于B,
由切线长定理知,∠1=∠2,PA=PB,
∴△ABP是等腰三角形,
∵∠1=∠2,
∴AB⊥OP(等腰三角形三线合一),
故A,B,C正确,
根据切割线定理知:=PC (PO+OC),因此D错误.
故选D.
5.A
【分析】先证得四边形为正方形;再设的半径为r,由勾股定理得,解此方程即可求得答案.
【详解】解:由题意得,是直角三角形,且,设内切圆与三边分别切于点D,E,F,连接,,如图,
∵是的内切圆,
∴,,
∴,
∵,
∴四边形为矩形,
∵,
∴矩形为正方形;
设的半径为r,
∵四边形为正方形,
∴,
∵是的内切圆,
∴,,
∴,,,
在中,,
∴,
解得:(舍去),
∴的半径为2;
故选:A.
【点睛】此题考查了三角形的内切圆的性质、切线长定理、正方形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.
6.D
【分析】连接,,根据切线长定理可得,再证明,问题得解.
【详解】连接,,如图,
∵切于,切于,
∴,即是等腰三角形,
∵,,
∴,
∴,即平分,
∴,即A、B、C三项都正确,
故选:D.
【点睛】本题主要考查了切线长定理,等腰三角形的判定与性质,全等三角形的判定与性质等知识,掌握切线长定理,是解答本题的关键.
7.C
【分析】先利用切线长定理得到,再利用可判断为等边三角形,然后根据等边三角形的性质求解.
【详解】解:,PB为的切线,
,
,
为等边三角形,
.
故选C.
【点睛】本题考查切线长定理,掌握切线长定理是解题的关键.
8.D
【详解】根据切线长定理可知PA=PB,故①正确;
同理可知CA=CE,可知CO为∠ACE的角平分线,所以∠ACO=∠DCO,故②正确;
同理可知DE=BD,由切线的性质可知∠OBD=∠OED=90°,可根据四边形的内角和为360°知∠BOE+∠BDE=180°,即∠BOE和∠BDE互补,故③正确;
根据切线长定理可得CE=CA,BD=DE,而△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+AC+PD+DB=PA+PB=2PB,故④正确.
故选D.
9.D
【分析】直接利用切线长定理得出AC=EC,BD=DE,AP=BP,进而求出答案.
【详解】∵P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,
∴AC=EC,BD=DE,AP=BP,
∵PA=15,∴△PCD的周长为:PA+PB=30.
故选D.
【点睛】此题主要考查了切线长定理,得出△PCD的周长为:PA+PB是解题关键.
10.C
【分析】如图所示,连接CP,由切线的性质和切线长定理得到∠CPO=90°,∠COP=45°,由此推出CP=OP=4,再根据勾股定理求解即可.
【详解】解:如图所示,连接CP,
∵OA,OB都是圆C的切线,∠AOB=90°,P为切点,
∴∠CPO=90°,∠COP=45°,
∴∠PCO=∠COP=45°,
∴CP=OP=4,
∴,
故选C.
【点睛】本题主要考查了切线的性质,切线长定理,等腰直角三角形的性质与判定,勾股定理,熟知切线长定理是解题的关键.
11.D
【分析】根据切线长定理直接求得PB=PA=5.
【详解】∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故选:D.
【点睛】本题考查了切线长定理,熟练掌握切线长定理是解题的关键.
12.B
【分析】根据切线长定理得到AF=AD=2,BD=BE,CE=CF,根据BC=5即可得到△ABC的周长.
【详解】解:∵△ABC的内切圆⊙O分别与AB,BC,AC相切于点D,E,F,且AD=2,
∴AF=AD=2,BD=BE,CE=CF,
∵BE+CE=BC=5,
∴BD+CF=BE+CE =BC=5,
∴△ABC的周长=2+2+5+5=14,
故选:B.
【点睛】本题考查切线长定理,熟练掌握切线长定理是解题的关键.
13.3
【分析】运用等腰直角三角形的性质和内心、外心的定义来解答,首先根据面积求出内切圆的半径,再利用勾股定理求出外接圆的半径,最后求解.
【详解】如图,∵AB=6,AC=BC,∠ABC=90°
∴CO1= AO1= BO1=3
AC=BC=
∵O2是内心,
∴
∴r=3-3
即O1O2=3-3
故答案为3-3
【点睛】此题主要考查了三角形的内心和外心,掌握等腰直角三角形的性质和三角形内切圆的半径的求法是解题关键.
14.120°
【解析】略
15.10cm
【分析】根据平行线的性质以及切线长定理,即可证明,再根据勾股定理即可求得的长,再结合切线长定理即可求解.
【详解】解: ,
,
、,分别与相切于、、,
,,,,
,
,
,
.
故答案为:10cm.
【点睛】此题主要是考查了切线长定理.从圆外一点引圆的两条切线,它们的切线长相等,且圆心和这点的连线平分两条切线的夹角.
16.2
【分析】根据切线长定理,可判断①正确;将的周长转化为,可判断②错误;连接、、,求出,再由,可判断③正确.
【详解】解:、是的切线,
,故①正确;
、、是的切线,
,,
的周长,故②错误;
连接、、,
,
,故③正确.
综上可得①③正确,共2个.
故选:.
【点睛】本题考查了切线的性质及切线长定理,熟悉相关性质是解答本题的关键.
17.48
【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=24,根据四边形的周长公式计算,得到答案.
【详解】解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=24,
∴四边形ABCD的周长=AD+BC+AB+CD=24+24=48,
故答案为:48.
【点睛】本题考查了切线长定理,掌握从圆外一点引圆的两条切线,它们的切线长相等是解题的关键.
18.(1)见解析;(2)直线ED与⊙O相切,理由见解析;(3)2
【分析】(1)说明∠DCE=∠DAB, ∠DAB=∠ACD,从而说明CD平分∠ACE;(2)连接OD,利用∠EDC+∠DCE=90°,∠DCE=∠ACD=∠ODC,从而∠EDC+∠ODC=90°;(3)延长DO交AB于点H,求出BD的长,即BE的长,CE=BE-BC.
【详解】(1)∵四边形ABCD是⊙O内接四边形,∴∠BAD+∠BCD=180°,
又∵∠BCD+∠DCE=180°, ∴∠DCE=∠BAD,
∵=, ∴∠BAD=∠ACD,
∴∠DCE=∠ACD, ∴CD平分∠ACE.
(2)直线ED与⊙O相切.连接OD.
∵OC=OD,∴∠ODC=∠OCD,
又∵∠DCE=∠ACD,∴∠DCE=∠ODC,
∴OD∥BE,∴∠ODE=∠DEC,
又∵DE⊥BC,∴∠DEC=90°,
∴∠ODE=90° ∴OD⊥DE,
∴ED与⊙O相切.
(3)延长DO交AB于点H.
∵OD∥BE,O是AC的中点,
∴H是AB的中点,
∴HO是△ABC的中位线,
∴HO=BC=3,
又∵AC为直径, ∴∠ADC=90°,
又∵O是AC的中点
∴OD=AC=×=5,
∴HD=3+5=8,
∵∠ABC=∠DEC=∠ODE=90°,
∴四边形BEDH是矩形,
∴BE=HD=8,
∴CE=8﹣6=2.
【点睛】此题考查了圆的综合题,涉及的知识有:坐标与图形性质,勾股定理,以及圆周角性质、矩形的判定.
19.6
【分析】连接CB.由切线长定理知PA=PB;又∠P=60°,则等腰三角形APB是等边三角形,则有ABP=60°;由弦切角定理知,∠PAB=∠C=60°,AC是直径;由直径对的圆周角是直角得∠ABC=90°,则在Rt△ABC中,有∠CAB=30°,进而可得结论.
【详解】连接CB.
∵PA、PB是⊙O的切线,∴PA=PB,
又∵∠P=60°,∴∠PAB=60°;
又∵AC是⊙O的直径,∴CA⊥PA,∠ABC=90°,∴∠CAB=30°,
而AC=12,∴在Rt△ABC中,cos30°=,∴AB=12×=6.
【点睛】本题考查了切线长定理,等边三角形的判定和性质,弦切角定理,直角三角形的性质.注意本题的解法不唯一.
20.
【分析】设光盘的圆心为O,光盘与三角尺的切点为C,连接.则,,进而根据切线长定理,可得,证明,从而得到,在中,解直角三角形即可求得,进而求得光盘的直径.
【详解】如图,设光盘的圆心为O,光盘与三角尺的切点为C,连接,则,,
是的切线
,
在中,.
的直径为.
答:这张光盘的直径是.
【点睛】本题考查了切线长定理,解直角三角形,掌握切线长定理是解题的关键.
21.(1)证明见解析;(2)证明见解析.
【详解】(1)证明:∵∠ABC=90°,
∴OB⊥BC
∵OB是⊙O的半径,
∴CB为⊙O的切线.
又∵CD切⊙O于点D,
∴BC=CD;
(2)证明:∵BE是⊙O的直径,
∴∠BDE=90°.
∴∠ADE+∠CDB=90°.
又∵∠ABC=90°,
∴∠ABD+∠CBD=90°.
由(1)得BC=CD,
∴∠CDB=∠CBD
∴∠ADE=∠ABD;
考点:切线的判定与性质.
22.,
【分析】根据切线的性质,得到,利用互余关系求出的度数,利用切线长定理,得到是等腰三角形,利用三角形内角和求出的度数即可.
【详解】解:∵是⊙O的切线,
∴,
∴,
∴,
∴.
【点睛】本题考查切线的性质和切线长定理.熟练掌握切线的性质和切线长定理是解题的关键.
23.(1)90°;(2)
【分析】(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;
(2)由勾股定理可求得BC的长,再根据三角形的面积,即可求得半径.
【详解】解:(1)连接OF;
根据切线长定理得:BE=BF,CF=CG,
∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°;
(2)∵OB=6cm,OC=8cm,
∴BC=10cm,
故半径为:4.8.
【点睛】此题主要是综合运用了切线长定理和切线的性质定理.由勾股定理可求得BC的长是关键.
24.(1)6;(2)1
【分析】(1)由切线长定理可得,,,再由△PEF的周长为12,即可得到,由此即可得到答案;
(2)连接OA、OB、OH、OP、OD、OG,设圆的半径为r,由,可以得到,再利用勾股定理求出,由此进行求解即可.
【详解】解:(1)由题意得,AP,BP,EF都是圆O的切线,
∴由切线长定理可得,,,
∵△PEF的周长为12,
∴,
∴;
(2)如图所示,连接OA、OB、OH、OP、OD、OG,设圆的半径为r,
∴OA=OB=OH=r,
由切线的性质可得OA⊥PD,OB⊥PG,OH⊥DG,
∴
,
∵∠G=90°,GD=3,GP=4,
∴,,
∴即,
∴,
∴⊙O的半径为1.
【点睛】本题主要考查了切线长定理,切线的性质,勾股定理,解题的关键在于能够熟练掌握切线长定理和切线的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
