3.2简单几何体的三视图同步练习(含解析)
文档属性
| 名称 | 3.2简单几何体的三视图同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 884.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
3.2简单几何体的三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中周长最小的是( )
A.主视图 B.左视图 C.俯视图 D.三种一样
2.如图所示的几何体,其左视图为( )
A. B. C. D.
3.一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的左视图为( )
A. B. C. D.
4.如图几何体的俯视图是( )
A. B. C. D.
5.如图是一个正五棱柱的主视图和左视图,该几何体的俯视图是( )
A. B. C. D.
6.用5个大小相同的小正方体搭一个几何体,其主视图、左视图如图2,现将其中4个小正方体按图1方式摆放,则最后一个小正方体应放在( )
A.①号位置 B.②号位置 C.③号位置 D.④号位置
7.如图,在下列四个几何体中,从正面、左面、上面看不完全相同的是
A. B. C. D.
8.如图,由相同的小正方体搭成的几何体的主视图是( )
A. B. C. D.
9.如图是一个机器零件,其主视图是( )
A. B. C. D.
10.斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
11.小明看到了“实验楼”三个字,而且能看到该楼所有的门窗,则小明看到的图是( )
A.俯视图; B.左视图; C.主视图; D.都有可能
12.如图是由几块小立方块所搭成的几何体的俯视图,小正方体中的数字表示该位置小立方块的个数,则该几何体的左视图是( )
A. B. C. D.
二、填空题
13.如图,是由8个大小相同的小正方体堆砌而成的几何体,现从标有①、②、③、④的四个小正方体中随机取走一个,所得新几何体与原几何体主视图相同的概率是 .
14.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有 种.
15.如图,已知圆锥的底面圆半径为l,则该圆锥的俯视图的面积为 .
16.主视图反映物体的 和 ,俯视图反映物体的 和 ,左视图反映物体的 和 .
17.如图是由一些相同的小立方体搭成的几何体,在其三种视图中,面积较小的是 视图.
三、解答题
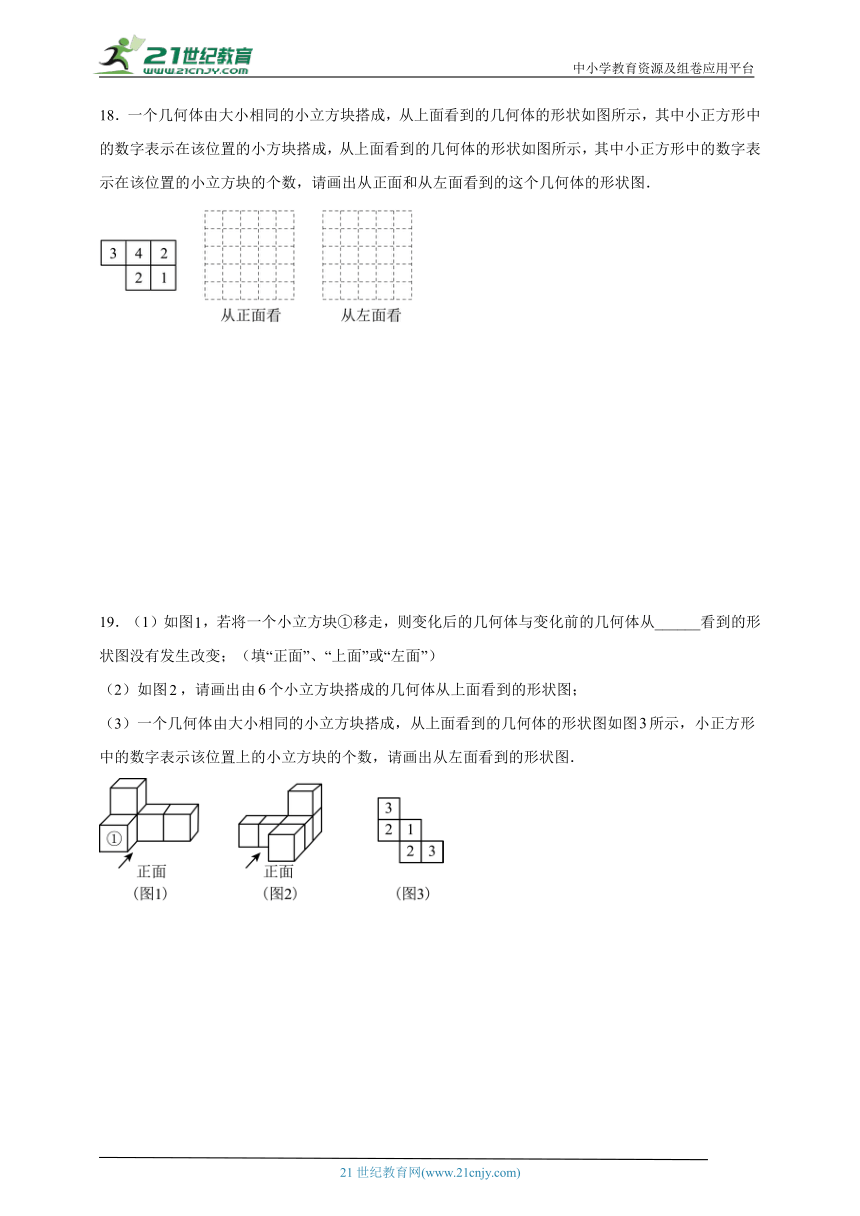
18.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
19.(1)如图,若将一个小立方块①移走,则变化后的几何体与变化前的几何体从______看到的形状图没有发生改变;(填“正面”、“上面”或“左面”)
(2)如图,请画出由个小立方块搭成的几何体从上面看到的形状图;
(3)一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,小正方形中的数字表示该位置上的小立方块的个数,请画出从左面看到的形状图.
20.如图,补全左视图与俯视图.
21.如图,在平整地面上,若干个完全相同的棱长为的小正方体堆成一个几何体.在下面网格中画出从三个方向看这个几何体得到的形状图.
22.画出如图所示的几何体的三种视图.
23.画出如图所示几何体的三种视图.
24.下列几何体的三种视图有没有错误(不考虑尺寸)?为什么?如果有错误,应该怎样改正?
(1)
(2)
《3.2简单几何体的三视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D A A B B D C C
题号 11 12
答案 C B
1.B
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【详解】解:如图,该几何体正视图是由5个小正方形组成,周长为12;左视图是由3个小正方形组成,周长为8;俯视图是由5个小正方形组成,周长为10;故三种视图周长最小的是左视图.
故选B.
【点睛】本题考查了几何体的三视图,正确从指定角度观察是解题的关键.
2.C
【分析】本题主要考查了简单几何体的三视图,理解视图的定义,掌握简单几何体三视图的画法和形状是解答此题的关键.根据简单几何体三视图的画法画出它的左视图即可.
【详解】解:这个几何体的左视图为:
故选:C.
3.D
【分析】由已知条件可知,左视图有3列,每列小正方形数目分别为2,3,3.据此可作出判断.
【详解】解:从左面看所得到的图形, .
故选:D.
【点睛】考查几何体的三视图的画法,从正面看的图形是主视图,从左面看到的图形是左视图,从上面看到的图形是俯视图.
4.A
【分析】此题主要考查了简单几何体的三视图,三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.注意所看到的线都要用实线表示出来.找到从几何体的上面看所得到图形即可.
【详解】解:从几何体的上面看到的图形即俯视图如图所示,
故选:A.
5.A
【分析】本题考查三视图,根据主左视图,画出俯视图,判断即可.
【详解】解:该几何体的俯视图是
故选A.
6.B
【分析】本题考查了由三视图判断几何体,掌握简单组合体三视图的画法和形状是正确解答的关键.根据题意主视图和左视图即可得到结论.
【详解】据主视图、左视图可知,最后一个小正方体应放在②号位置.
故选:B
7.B
【分析】根据常见几何体的三视图解答即可得.
【详解】球的三视图均为圆,故不符合题意;
正方体的三视图均为正方形,故不符合题意;
圆柱体的主视图与左视图为长方形,俯视图为圆,故符合题意;
圆锥的主视图与左视图为等腰三角形,俯视图为圆,故符合题意,
故选B.
【点睛】本题考查了简单几何体的三视图,解题的关键是熟练掌握三视图的定义和常见几何体的三视图.
8.D
【分析】根据从前面看到的图形是主视图解答即可.
【详解】主视图的第一层是三个正方形,第二层是中间有一个正方形.
故选D.
【点睛】本题考查了几何体的三视图,从前面看到的图形是主视图,从上面看到的图形是俯视图,从左边看到的图形是左视图.
9.C
【分析】根据三视图的概念进行判断即可.
【详解】
解:主视图为:
故选:C.
【点睛】本题考查了三视图,掌握从正面观察物体时,看到的图是主视图是解题的关键.
10.C
【分析】本题考查了简单组合体的三视图,利用三视图的定义是解题关键.
主视图:从正面看到的物体的形状图;左视图:从左面看到的物体的形状图;俯视图:从上面看到的物体的形状图.根据三视图的定义求解,注意看不见的线应当画虚线,即可.
【详解】解:从左面看,上面部分是矩形,下面部分是梯形,矩形部分有一条看不见的线,应该画虚线,形状如图所示:
故选:C.
11.C
【详解】试题分析:“实验楼”所有的门窗一般都是在正面,根据主视图是从正面看到的图形即可判断.
由题意得,小明的看到的图是主视图,故选C.
考点:本题考查的是几何体的三视图
点评:解答本题的关键是熟记主视图是从正面看到的图形,左视图是从左面边看到的图形,俯视图是从上面看到的图形.
12.B
【分析】本题考查了由三视图判断几何体,简单组合体的三视图,从左面看得到的图形是左视图.根据从左面看得到的图形是左视图,可得从左面看左边是2层小正方形,右边是3层小正方形,即可得到答案.
【详解】解:观察图形可知,该几何体的左视图是:
故选:B.
13./25%/0.25
【分析】根据题意得到原几何体的主视图,结合主视图在①、②、③、④选择符合题意的序号,从而得到答案.
【详解】原几何体的主视图是:
故取走正方体①使所得新几何体与原几何体主视图相同,其概率为,
故答案为:.
【点睛】本题考查了简单组合体的三视图.视图中每一个闭合的线框都表示物体上的一个平面,而相连的两个闭合线框常不在一个平面上,解题的关键是画出原几何体的主视图.
14.10
【分析】观察图形,根据几何体的主视图每一列最大分别为4,2,3再根据左视图确定每一列最大分别为4,3,2总数要保证是16,还要保证俯视图有9个位置,从而即可得出所有的不同搭法.
【详解】解:设俯视图有9个位置分别为:
由主视图和左视图知:①第1个位置一定是4,第6个位置一定是3;
②一定有2个2,其余有5个1;
③最后一行至少有一个2,当中一列至少有一个2;
根据2的排列不同,这个几何体的搭法共有10种:如下图所示:
故答案为10.
【点睛】本题主要考查由三视图判断几何体.解题关键是根据主视图与左视图相同小方块数的交叉列确定不变的小立方块数量在什么位置.
15.
【分析】根据圆锥的俯视图,圆的面积公式即可得出结果.
【详解】解:圆锥的俯视图的面积等于半径为l圆的面积,
该圆锥的俯视图的面积为,
故答案为:.
【点睛】本题考查了立体图形的三视图,圆的面积公式.根据立体图形判断出俯视图是本题的关键.
16. 长 高 长 宽 宽 高
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,那么主视图反映几何体的长与高,左视图反映几何体的高与宽,俯视图反映几何体的长与宽,都有高的视图中的高相等,都有宽的视图中的宽相等.
【详解】解:主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.因此,必须注意主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
故答案为(1). 长 (2). 高 (3). 长 (4). 宽 (5). 宽 (6). 高
【点睛】本题考查三视图反映几何体的长宽高的情况,注意“长对正,宽相等,高平齐”的知识点.
17.主
【分析】分别画出几何体的三视图,然后比较,哪个的面最少则面积最小.
【详解】解:如图一、二、三,分别是几何体的主视图、左视图和俯视图,
主视图有3个正方形组成,左视图、俯视图都有4个正方形组成;
因为几何体是由一些相同的小立方体搭成的,
所以面积最小的是主视图.
故答案为:主.
【点睛】本题考查了简单组合体的三视图,几何体的主视图、左视图和俯视图,是分别从几何体的正面、左面和上面看物体而得到的图形,考查了学生的空间想象能力.
18.见解析
【分析】主视图有3列,从左到右每列小正方形数目分别为3,4,2,左视图有2列,从左到右每列小正方数形数目分别为4,2,据此可画出图形.
【详解】解:如图所示:
.
【点睛】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
19.(1)正面
(2)见解析
(2)见解析
【分析】(1)根据三视图的定义判断即可;
(2)根据三视图的定义,画出图形即可;
(3)根据三视图的定义,画出图形即可.
【详解】解:(1)如图1,将一个正方体①移走后,变化后的几何体与变化前的几何体从正面看到的形状图相同.
故答案为:正面;
(2)如图所示:
(3)如图所示:
【点睛】本题考查作图﹣三视图,解题的关键是理解三视图的定义,属于中考常考题型.
20.补图见解析.
【详解】分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;认真观察实物图,按照三视图的要求画图即可,注意看得到的棱长用实线表示,看不到的棱长用虚线的表示.
详解:补全视图,如答图所示.
点睛:此题主要考查了三视图的画法,注意实线和虚线在三视图的用法.
21.见解析
【分析】本题考查作图-三视图,几何体的表面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.分从正面,上面,左面三个方向统计正方形的个数即可.
【详解】解:如图所示:
22.见解析
【分析】利用已知几何体分别得出三种不同的视图即可.
【详解】解:(1)三视图如下图所示:
(2)三视图如下图所示:
【点睛】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
23.(1)见解析;(2)见解析
【分析】画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.要注意几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线画成虚线.
【详解】(1)如图所示:
(2)如图所示:
【点睛】本题考查了作图 三视图的画法,注意实线和虚线在三视图的用法.
24.(1)不正确,答案见解析;(2)不正确,答案见解析
【分析】分别从正面、左面、上面看即可得到三视图,注意看的见的轮廓线都画成实线,看不见的画成虚线即可求解.
【详解】解:(1)不正确;由题意可知,正确的三视图如下所示:
(2)不正确;由题意可知,正确的三视图如下所示:
【点睛】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.2简单几何体的三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中周长最小的是( )
A.主视图 B.左视图 C.俯视图 D.三种一样
2.如图所示的几何体,其左视图为( )
A. B. C. D.
3.一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的左视图为( )
A. B. C. D.
4.如图几何体的俯视图是( )
A. B. C. D.
5.如图是一个正五棱柱的主视图和左视图,该几何体的俯视图是( )
A. B. C. D.
6.用5个大小相同的小正方体搭一个几何体,其主视图、左视图如图2,现将其中4个小正方体按图1方式摆放,则最后一个小正方体应放在( )
A.①号位置 B.②号位置 C.③号位置 D.④号位置
7.如图,在下列四个几何体中,从正面、左面、上面看不完全相同的是
A. B. C. D.
8.如图,由相同的小正方体搭成的几何体的主视图是( )
A. B. C. D.
9.如图是一个机器零件,其主视图是( )
A. B. C. D.
10.斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
11.小明看到了“实验楼”三个字,而且能看到该楼所有的门窗,则小明看到的图是( )
A.俯视图; B.左视图; C.主视图; D.都有可能
12.如图是由几块小立方块所搭成的几何体的俯视图,小正方体中的数字表示该位置小立方块的个数,则该几何体的左视图是( )
A. B. C. D.
二、填空题
13.如图,是由8个大小相同的小正方体堆砌而成的几何体,现从标有①、②、③、④的四个小正方体中随机取走一个,所得新几何体与原几何体主视图相同的概率是 .
14.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有 种.
15.如图,已知圆锥的底面圆半径为l,则该圆锥的俯视图的面积为 .
16.主视图反映物体的 和 ,俯视图反映物体的 和 ,左视图反映物体的 和 .
17.如图是由一些相同的小立方体搭成的几何体,在其三种视图中,面积较小的是 视图.
三、解答题
18.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
19.(1)如图,若将一个小立方块①移走,则变化后的几何体与变化前的几何体从______看到的形状图没有发生改变;(填“正面”、“上面”或“左面”)
(2)如图,请画出由个小立方块搭成的几何体从上面看到的形状图;
(3)一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,小正方形中的数字表示该位置上的小立方块的个数,请画出从左面看到的形状图.
20.如图,补全左视图与俯视图.
21.如图,在平整地面上,若干个完全相同的棱长为的小正方体堆成一个几何体.在下面网格中画出从三个方向看这个几何体得到的形状图.
22.画出如图所示的几何体的三种视图.
23.画出如图所示几何体的三种视图.
24.下列几何体的三种视图有没有错误(不考虑尺寸)?为什么?如果有错误,应该怎样改正?
(1)
(2)
《3.2简单几何体的三视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D A A B B D C C
题号 11 12
答案 C B
1.B
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【详解】解:如图,该几何体正视图是由5个小正方形组成,周长为12;左视图是由3个小正方形组成,周长为8;俯视图是由5个小正方形组成,周长为10;故三种视图周长最小的是左视图.
故选B.
【点睛】本题考查了几何体的三视图,正确从指定角度观察是解题的关键.
2.C
【分析】本题主要考查了简单几何体的三视图,理解视图的定义,掌握简单几何体三视图的画法和形状是解答此题的关键.根据简单几何体三视图的画法画出它的左视图即可.
【详解】解:这个几何体的左视图为:
故选:C.
3.D
【分析】由已知条件可知,左视图有3列,每列小正方形数目分别为2,3,3.据此可作出判断.
【详解】解:从左面看所得到的图形, .
故选:D.
【点睛】考查几何体的三视图的画法,从正面看的图形是主视图,从左面看到的图形是左视图,从上面看到的图形是俯视图.
4.A
【分析】此题主要考查了简单几何体的三视图,三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.注意所看到的线都要用实线表示出来.找到从几何体的上面看所得到图形即可.
【详解】解:从几何体的上面看到的图形即俯视图如图所示,
故选:A.
5.A
【分析】本题考查三视图,根据主左视图,画出俯视图,判断即可.
【详解】解:该几何体的俯视图是
故选A.
6.B
【分析】本题考查了由三视图判断几何体,掌握简单组合体三视图的画法和形状是正确解答的关键.根据题意主视图和左视图即可得到结论.
【详解】据主视图、左视图可知,最后一个小正方体应放在②号位置.
故选:B
7.B
【分析】根据常见几何体的三视图解答即可得.
【详解】球的三视图均为圆,故不符合题意;
正方体的三视图均为正方形,故不符合题意;
圆柱体的主视图与左视图为长方形,俯视图为圆,故符合题意;
圆锥的主视图与左视图为等腰三角形,俯视图为圆,故符合题意,
故选B.
【点睛】本题考查了简单几何体的三视图,解题的关键是熟练掌握三视图的定义和常见几何体的三视图.
8.D
【分析】根据从前面看到的图形是主视图解答即可.
【详解】主视图的第一层是三个正方形,第二层是中间有一个正方形.
故选D.
【点睛】本题考查了几何体的三视图,从前面看到的图形是主视图,从上面看到的图形是俯视图,从左边看到的图形是左视图.
9.C
【分析】根据三视图的概念进行判断即可.
【详解】
解:主视图为:
故选:C.
【点睛】本题考查了三视图,掌握从正面观察物体时,看到的图是主视图是解题的关键.
10.C
【分析】本题考查了简单组合体的三视图,利用三视图的定义是解题关键.
主视图:从正面看到的物体的形状图;左视图:从左面看到的物体的形状图;俯视图:从上面看到的物体的形状图.根据三视图的定义求解,注意看不见的线应当画虚线,即可.
【详解】解:从左面看,上面部分是矩形,下面部分是梯形,矩形部分有一条看不见的线,应该画虚线,形状如图所示:
故选:C.
11.C
【详解】试题分析:“实验楼”所有的门窗一般都是在正面,根据主视图是从正面看到的图形即可判断.
由题意得,小明的看到的图是主视图,故选C.
考点:本题考查的是几何体的三视图
点评:解答本题的关键是熟记主视图是从正面看到的图形,左视图是从左面边看到的图形,俯视图是从上面看到的图形.
12.B
【分析】本题考查了由三视图判断几何体,简单组合体的三视图,从左面看得到的图形是左视图.根据从左面看得到的图形是左视图,可得从左面看左边是2层小正方形,右边是3层小正方形,即可得到答案.
【详解】解:观察图形可知,该几何体的左视图是:
故选:B.
13./25%/0.25
【分析】根据题意得到原几何体的主视图,结合主视图在①、②、③、④选择符合题意的序号,从而得到答案.
【详解】原几何体的主视图是:
故取走正方体①使所得新几何体与原几何体主视图相同,其概率为,
故答案为:.
【点睛】本题考查了简单组合体的三视图.视图中每一个闭合的线框都表示物体上的一个平面,而相连的两个闭合线框常不在一个平面上,解题的关键是画出原几何体的主视图.
14.10
【分析】观察图形,根据几何体的主视图每一列最大分别为4,2,3再根据左视图确定每一列最大分别为4,3,2总数要保证是16,还要保证俯视图有9个位置,从而即可得出所有的不同搭法.
【详解】解:设俯视图有9个位置分别为:
由主视图和左视图知:①第1个位置一定是4,第6个位置一定是3;
②一定有2个2,其余有5个1;
③最后一行至少有一个2,当中一列至少有一个2;
根据2的排列不同,这个几何体的搭法共有10种:如下图所示:
故答案为10.
【点睛】本题主要考查由三视图判断几何体.解题关键是根据主视图与左视图相同小方块数的交叉列确定不变的小立方块数量在什么位置.
15.
【分析】根据圆锥的俯视图,圆的面积公式即可得出结果.
【详解】解:圆锥的俯视图的面积等于半径为l圆的面积,
该圆锥的俯视图的面积为,
故答案为:.
【点睛】本题考查了立体图形的三视图,圆的面积公式.根据立体图形判断出俯视图是本题的关键.
16. 长 高 长 宽 宽 高
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,那么主视图反映几何体的长与高,左视图反映几何体的高与宽,俯视图反映几何体的长与宽,都有高的视图中的高相等,都有宽的视图中的宽相等.
【详解】解:主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.因此,必须注意主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
故答案为(1). 长 (2). 高 (3). 长 (4). 宽 (5). 宽 (6). 高
【点睛】本题考查三视图反映几何体的长宽高的情况,注意“长对正,宽相等,高平齐”的知识点.
17.主
【分析】分别画出几何体的三视图,然后比较,哪个的面最少则面积最小.
【详解】解:如图一、二、三,分别是几何体的主视图、左视图和俯视图,
主视图有3个正方形组成,左视图、俯视图都有4个正方形组成;
因为几何体是由一些相同的小立方体搭成的,
所以面积最小的是主视图.
故答案为:主.
【点睛】本题考查了简单组合体的三视图,几何体的主视图、左视图和俯视图,是分别从几何体的正面、左面和上面看物体而得到的图形,考查了学生的空间想象能力.
18.见解析
【分析】主视图有3列,从左到右每列小正方形数目分别为3,4,2,左视图有2列,从左到右每列小正方数形数目分别为4,2,据此可画出图形.
【详解】解:如图所示:
.
【点睛】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
19.(1)正面
(2)见解析
(2)见解析
【分析】(1)根据三视图的定义判断即可;
(2)根据三视图的定义,画出图形即可;
(3)根据三视图的定义,画出图形即可.
【详解】解:(1)如图1,将一个正方体①移走后,变化后的几何体与变化前的几何体从正面看到的形状图相同.
故答案为:正面;
(2)如图所示:
(3)如图所示:
【点睛】本题考查作图﹣三视图,解题的关键是理解三视图的定义,属于中考常考题型.
20.补图见解析.
【详解】分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;认真观察实物图,按照三视图的要求画图即可,注意看得到的棱长用实线表示,看不到的棱长用虚线的表示.
详解:补全视图,如答图所示.
点睛:此题主要考查了三视图的画法,注意实线和虚线在三视图的用法.
21.见解析
【分析】本题考查作图-三视图,几何体的表面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.分从正面,上面,左面三个方向统计正方形的个数即可.
【详解】解:如图所示:
22.见解析
【分析】利用已知几何体分别得出三种不同的视图即可.
【详解】解:(1)三视图如下图所示:
(2)三视图如下图所示:
【点睛】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
23.(1)见解析;(2)见解析
【分析】画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.要注意几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线画成虚线.
【详解】(1)如图所示:
(2)如图所示:
【点睛】本题考查了作图 三视图的画法,注意实线和虚线在三视图的用法.
24.(1)不正确,答案见解析;(2)不正确,答案见解析
【分析】分别从正面、左面、上面看即可得到三视图,注意看的见的轮廓线都画成实线,看不见的画成虚线即可求解.
【详解】解:(1)不正确;由题意可知,正确的三视图如下所示:
(2)不正确;由题意可知,正确的三视图如下所示:
【点睛】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
