浙教版七年级上册 4.1 列代数式 课件(共19张PPT)
文档属性
| 名称 | 浙教版七年级上册 4.1 列代数式 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 719.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 15:02:18 | ||
图片预览




文档简介
(共19张PPT)
4.1 列代数式
浙教新版七年级《数学》上册
(1)大米的单价为 a 元/千克,食用油的单价为 b 元/千克.买 10 千克大米、2 千克食用油共需_________元.
(2)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值.若上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数是_____________ .
10a+2b
合作学习
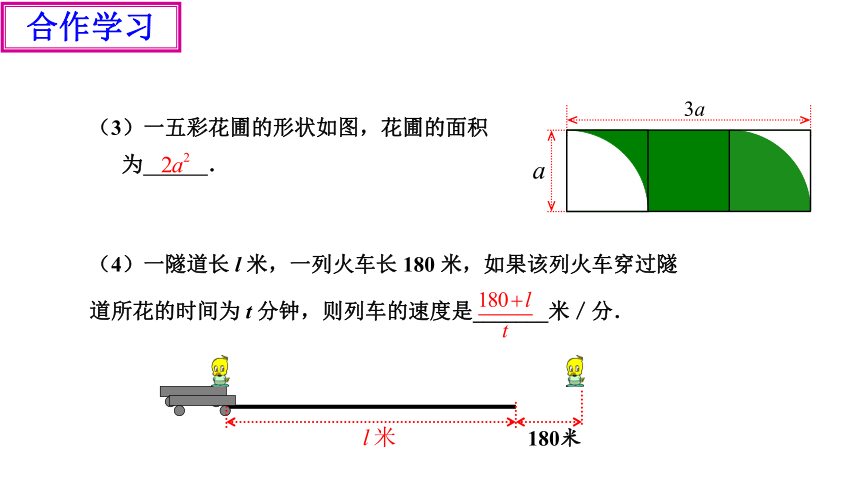
(3)一五彩花圃的形状如图,花圃的面积
为 .
(4)一隧道长 l 米,一列火车长 180 米,如果该列火车穿过隧
道所花的时间为 t 分钟,则列车的速度是_______米/分.
180米
合作学习
(10a+2b),
a+b+c+d
————,
4
2a2,
由数、表示数的字母和运算符号组成的数学表达式称为代数式.
这里的运算是指加、减、乘、除、乘方和开方,单独一个数或者一个字母也称代数式.
像 这样,
形成概念
单独一个数或一个字母也是代数式.
代数式不含“=”、“>”、“<”、“≤”、“≥”、“≠”.
代数式中可以含有括号.
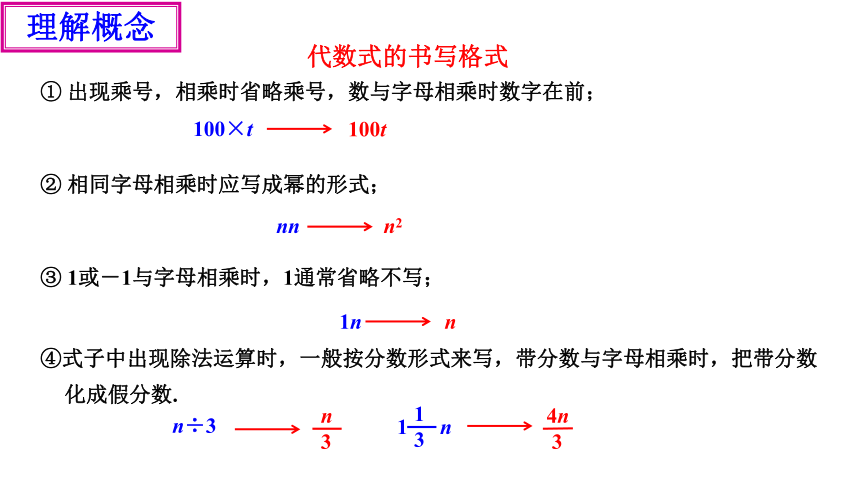
① 出现乘号,相乘时省略乘号,数与字母相乘时数字在前;
② 相同字母相乘时应写成幂的形式;
③ 1或-1与字母相乘时,1通常省略不写;
④式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
100×t
100t
nn
n2
1n
n
n÷3
n
3
1
3
1 n
4n
3
理解概念
代数式的书写格式
下列各式中哪些是代数式?哪些不是?
(1) m+5 (2)a+b=b+a
(3)0 (4)x2+3x+4
(5) x+y>1 (6)
√
×
√
√
√
×
感悟新知
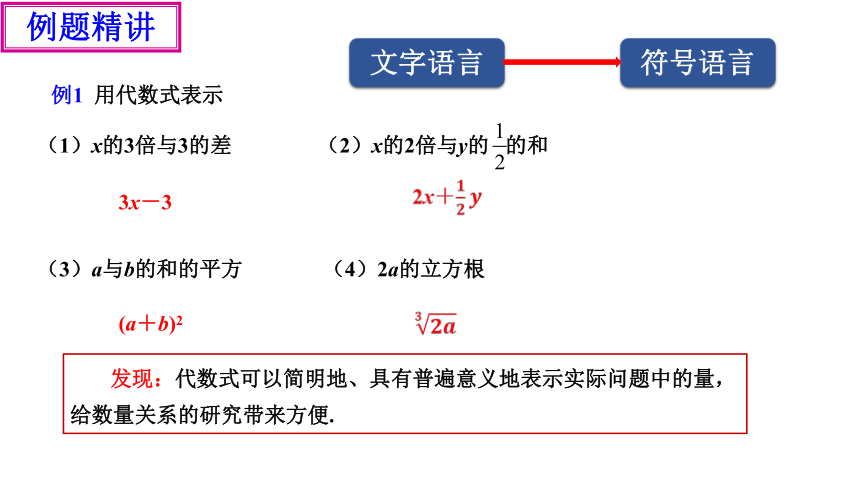
例1 用代数式表示
(1)x的3倍与3的差 (2)x的2倍与y的 的和
(3)a与b的和的平方 (4)2a的立方根
3x-3
(a+b)2
2x+
发现:代数式可以简明地、具有普遍意义地表示实际问题中的量,给数量关系的研究带来方便.
例题精讲
文字语言
符号语言
例2 一辆汽车以 80 千米/时的速度行驶,从A城到B城需t时.如果该车的行驶速
度增加 v (千米/时),那么从A城到B城需多少时间
解:由题意得,A,B两城之间的路程为80t(km).如果该车的行驶速度增加v(km/h),那么汽车的行驶速度为(80+v)km/h,此时从A城到B城需要(h).
答:当该车行驶速度增加v(km/h),从A城到B城需.
例题精讲
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳总结
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
从上面例子看出,代数式中可以用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
字母表示数(代数式)
更简明
更一般化
1.用代数式表示:
(1)x与y的平方的差;
(2)x与y的差的平方;
(3)m与1的差的算术平方根;
(4)m的相反数与n的 倍的差;
(5)x的2倍与y的3倍的和.
解:(1) ; (2) ; (3) ;
(4) ; (5) .
知识应用
2.学校小商店内的钢笔每支卖a元,圆珠笔每支卖b元.
(1)小华买了3支圆珠笔和2支钢笔,则他共用多少元?
解 小华买3支圆珠笔和2支钢笔共用(2a+3b)元.
(2)若他手里只有一张100元的人民币,那么商店应该找回多少元钱?
解 商店应该找回(100-2a-3b)元.
知识应用
3.根据你的生活与学习经验,对代数式 2(x+y)表示的实际意义作出两种不同的解释.
例:某水果超市推出两款促销水果,其中苹果每斤x元,香蕉每斤y元,小明买了2斤苹果和2斤香蕉,共花去2(x+y)元钱.
知识应用
通过本节课的学习,你有哪些收获、体会或疑问?
有理数(数)
用字母 表示数
代数式
3n+1
3n+1=13
3n+1<13
y=3n+1
方程
不等式
函数
利用字母表示数从算术到代数的一大飞跃.
能把数和数量关系、数学规律一般化地、简明地表示出来.
小结提升
课后作业
3.“比a的2倍大1的数”用式子表示是( )
A. 2(a+1) B. 2(a-1) C. 2a+1 D. 2a-1
C
2.下列各式符合书写规范的是( )
A. ab B. a×3 C. 3x-1个 D. x
A
1.下列各式中,是代数式的是 ( )
A.a(c+b)=ac+ab B.3x-1=0
C.1-3x D.3ab>5
C
(1)5箱苹果共重m kg,每箱重 kg ;
(2)一个数比a的2倍小5,则这个数为 ;
(3)某商品的原价是a元,降价10%后的价格是 .
4.用式子表示下列数量
2a-5
(1-10%)a
课后作业
5.体育委员小金带了500元去买足球和篮球,已知足球每个x元,篮
球每个y元.试解释一下式子500-3x-2y表示的实际意义.
课后作业
小金买了3个足球和2个篮球,还剩这么多钱.
6.老师为学校买排球,排球单价为每个a 元,买10个以上按8折优惠.
(1)购买25个排球应付多少钱?(2)购买b个排球应付多少钱?
解:(1) 因为25>10,
所以购买25个排球应付25a×0.8=20a 元
(2)有两种情况:
① 当b≤10时,应付ab 元;
② 当b>10时,应付0.8ab 元.
课后作业
(1)1 张饭桌可坐6 人,2 张饭桌可坐 人;
(2)按图中的方式摆放桌子和椅子,n 张饭桌可坐 人.
4n+2
10
课后作业
7. 学校餐厅准备按图的方式摆放桌子和椅子,请按图中提示,
回答下列问题:
韦达(1540—1603),法国数学家,第一个有意识地和系统地使用字母来表示数.
算 术
代 数
具 体
抽 象
一次飞跃
小结提升
4.1 列代数式
浙教新版七年级《数学》上册
(1)大米的单价为 a 元/千克,食用油的单价为 b 元/千克.买 10 千克大米、2 千克食用油共需_________元.
(2)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值.若上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数是_____________ .
10a+2b
合作学习
(3)一五彩花圃的形状如图,花圃的面积
为 .
(4)一隧道长 l 米,一列火车长 180 米,如果该列火车穿过隧
道所花的时间为 t 分钟,则列车的速度是_______米/分.
180米
合作学习
(10a+2b),
a+b+c+d
————,
4
2a2,
由数、表示数的字母和运算符号组成的数学表达式称为代数式.
这里的运算是指加、减、乘、除、乘方和开方,单独一个数或者一个字母也称代数式.
像 这样,
形成概念
单独一个数或一个字母也是代数式.
代数式不含“=”、“>”、“<”、“≤”、“≥”、“≠”.
代数式中可以含有括号.
① 出现乘号,相乘时省略乘号,数与字母相乘时数字在前;
② 相同字母相乘时应写成幂的形式;
③ 1或-1与字母相乘时,1通常省略不写;
④式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
100×t
100t
nn
n2
1n
n
n÷3
n
3
1
3
1 n
4n
3
理解概念
代数式的书写格式
下列各式中哪些是代数式?哪些不是?
(1) m+5 (2)a+b=b+a
(3)0 (4)x2+3x+4
(5) x+y>1 (6)
√
×
√
√
√
×
感悟新知
例1 用代数式表示
(1)x的3倍与3的差 (2)x的2倍与y的 的和
(3)a与b的和的平方 (4)2a的立方根
3x-3
(a+b)2
2x+
发现:代数式可以简明地、具有普遍意义地表示实际问题中的量,给数量关系的研究带来方便.
例题精讲
文字语言
符号语言
例2 一辆汽车以 80 千米/时的速度行驶,从A城到B城需t时.如果该车的行驶速
度增加 v (千米/时),那么从A城到B城需多少时间
解:由题意得,A,B两城之间的路程为80t(km).如果该车的行驶速度增加v(km/h),那么汽车的行驶速度为(80+v)km/h,此时从A城到B城需要(h).
答:当该车行驶速度增加v(km/h),从A城到B城需.
例题精讲
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳总结
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
从上面例子看出,代数式中可以用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
字母表示数(代数式)
更简明
更一般化
1.用代数式表示:
(1)x与y的平方的差;
(2)x与y的差的平方;
(3)m与1的差的算术平方根;
(4)m的相反数与n的 倍的差;
(5)x的2倍与y的3倍的和.
解:(1) ; (2) ; (3) ;
(4) ; (5) .
知识应用
2.学校小商店内的钢笔每支卖a元,圆珠笔每支卖b元.
(1)小华买了3支圆珠笔和2支钢笔,则他共用多少元?
解 小华买3支圆珠笔和2支钢笔共用(2a+3b)元.
(2)若他手里只有一张100元的人民币,那么商店应该找回多少元钱?
解 商店应该找回(100-2a-3b)元.
知识应用
3.根据你的生活与学习经验,对代数式 2(x+y)表示的实际意义作出两种不同的解释.
例:某水果超市推出两款促销水果,其中苹果每斤x元,香蕉每斤y元,小明买了2斤苹果和2斤香蕉,共花去2(x+y)元钱.
知识应用
通过本节课的学习,你有哪些收获、体会或疑问?
有理数(数)
用字母 表示数
代数式
3n+1
3n+1=13
3n+1<13
y=3n+1
方程
不等式
函数
利用字母表示数从算术到代数的一大飞跃.
能把数和数量关系、数学规律一般化地、简明地表示出来.
小结提升
课后作业
3.“比a的2倍大1的数”用式子表示是( )
A. 2(a+1) B. 2(a-1) C. 2a+1 D. 2a-1
C
2.下列各式符合书写规范的是( )
A. ab B. a×3 C. 3x-1个 D. x
A
1.下列各式中,是代数式的是 ( )
A.a(c+b)=ac+ab B.3x-1=0
C.1-3x D.3ab>5
C
(1)5箱苹果共重m kg,每箱重 kg ;
(2)一个数比a的2倍小5,则这个数为 ;
(3)某商品的原价是a元,降价10%后的价格是 .
4.用式子表示下列数量
2a-5
(1-10%)a
课后作业
5.体育委员小金带了500元去买足球和篮球,已知足球每个x元,篮
球每个y元.试解释一下式子500-3x-2y表示的实际意义.
课后作业
小金买了3个足球和2个篮球,还剩这么多钱.
6.老师为学校买排球,排球单价为每个a 元,买10个以上按8折优惠.
(1)购买25个排球应付多少钱?(2)购买b个排球应付多少钱?
解:(1) 因为25>10,
所以购买25个排球应付25a×0.8=20a 元
(2)有两种情况:
① 当b≤10时,应付ab 元;
② 当b>10时,应付0.8ab 元.
课后作业
(1)1 张饭桌可坐6 人,2 张饭桌可坐 人;
(2)按图中的方式摆放桌子和椅子,n 张饭桌可坐 人.
4n+2
10
课后作业
7. 学校餐厅准备按图的方式摆放桌子和椅子,请按图中提示,
回答下列问题:
韦达(1540—1603),法国数学家,第一个有意识地和系统地使用字母来表示数.
算 术
代 数
具 体
抽 象
一次飞跃
小结提升
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
