第一章 解直角三角形 训练试题(含解析)浙教版九年级数学下册
文档属性
| 名称 | 第一章 解直角三角形 训练试题(含解析)浙教版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 633.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览



文档简介
第一章 解直角三角形
一、单选题
1.如图,小明在数学兴趣小组探究活动中要测量河的宽度,他和同学在河对岸选定一点A,再在河的这一边选定点P和点B,使.利用工具测得米,,根据测量数据可计算得到小河宽度为( )
A.米 B.米 C.米 D.米
2.在△ABC中,∠C=90°,AC=1,BC=2,则 cos A的值是( )
A. B. C. D.
3.如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.右转80° B.左转80° C.右转100° D.左转100°
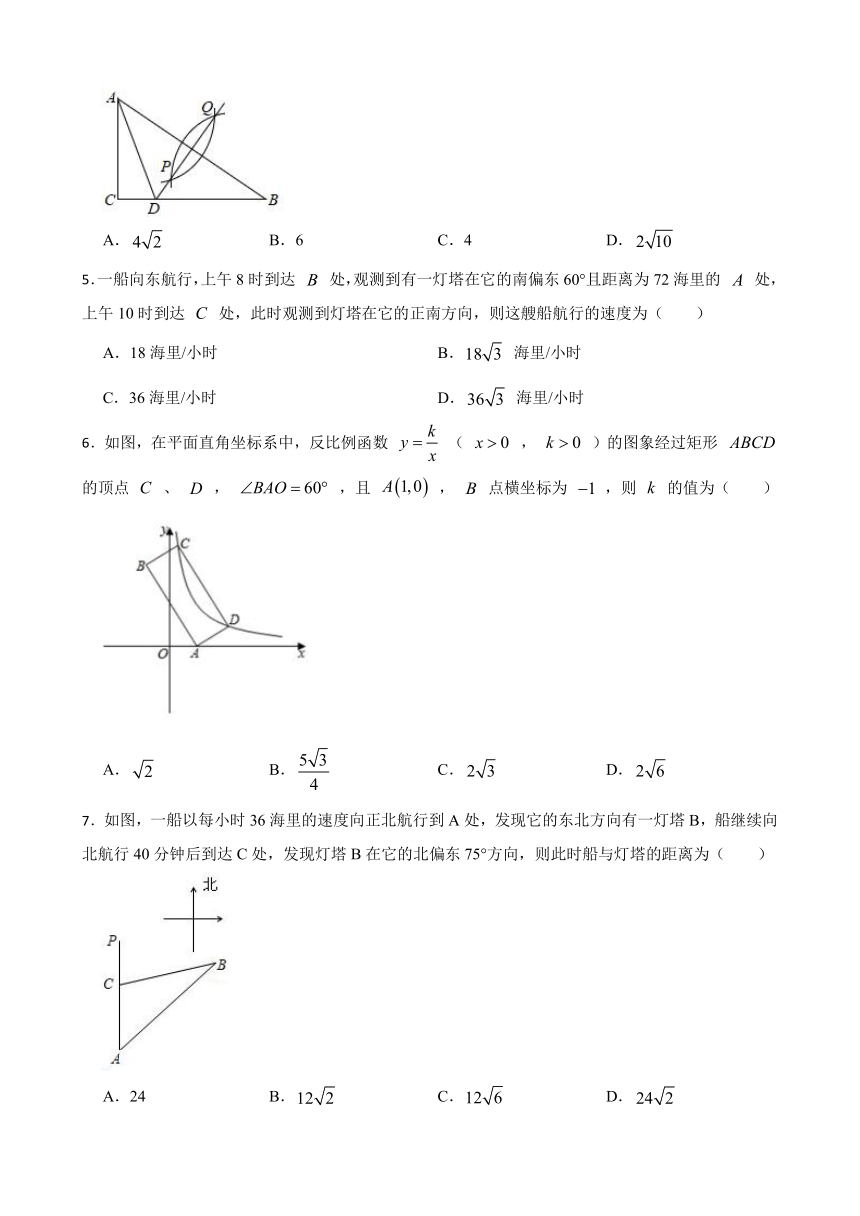
4.如图,在 中, ,按以下步骤作图:①分别以点 为圆心,大于 的长为半径作弧,两弧交于点 ;②作直线 交边 于点D,连接 ,若 ,则 的长为( )
A. B.6 C.4 D.
5.一船向东航行,上午8时到达 处,观测到有一灯塔在它的南偏东60°且距离为72海里的 处,上午10时到达 处,此时观测到灯塔在它的正南方向,则这艘船航行的速度为( )
A.18海里/小时 B. 海里/小时
C.36海里/小时 D. 海里/小时
6.如图,在平面直角坐标系中,反比例函数 ( , )的图象经过矩形 的顶点 、 , ,且 , 点横坐标为 ,则 的值为( )
A. B. C. D.
7.如图,一船以每小时36海里的速度向正北航行到A处,发现它的东北方向有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在它的北偏东75°方向,则此时船与灯塔的距离为( )
A.24 B. C. D.
8.如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于 CD的长为半径作弧,两弧相交于M、N两点;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE.则下列说法错误的是( )
A.∠ABC=60° B.S△ABE=2S△ADE
C.若AB=4,则BE= D.sin∠CBE=
9.如图,在一笔直的沿湖道路l上有、两个游船码头,观光岛屿在码头北偏东的方向,在码头北偏西的方向,.游客小张准备从观光岛屿乘船沿回到码头或沿回到码头,设开往码头、的游船速度分别为、,若回到、所用时间相等,则( )
A. B. C.4 D.6
10.如图是墙壁上在l1,l2两条平行线间的边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为α,则两条平行线间的距离为( )
A.2asinα B.asinα+acosα C.2acosα D.asinα-acosα
二、填空题
11.如果在A点处观察B点的仰角为,那么在B点处观察A点的俯角为 (用含的式子表示)
12.如图,一段铁路路基的横断面为等腰梯形,路基的上底宽AD为3米,路基高为1米,斜坡AB的坡度,那么路基的下底宽BC是 米.
13.计算:(﹣ )﹣2﹣|1﹣ |+4cos45°= .
14.如图,平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=6,AF=4,cos∠EAF= ,则CF= .
15.计算sin60°cos60°的值为 .
三、解答题
16.如图, 内接于⊙ .若⊙ 的半径为6, ,求 的长.
17.构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)
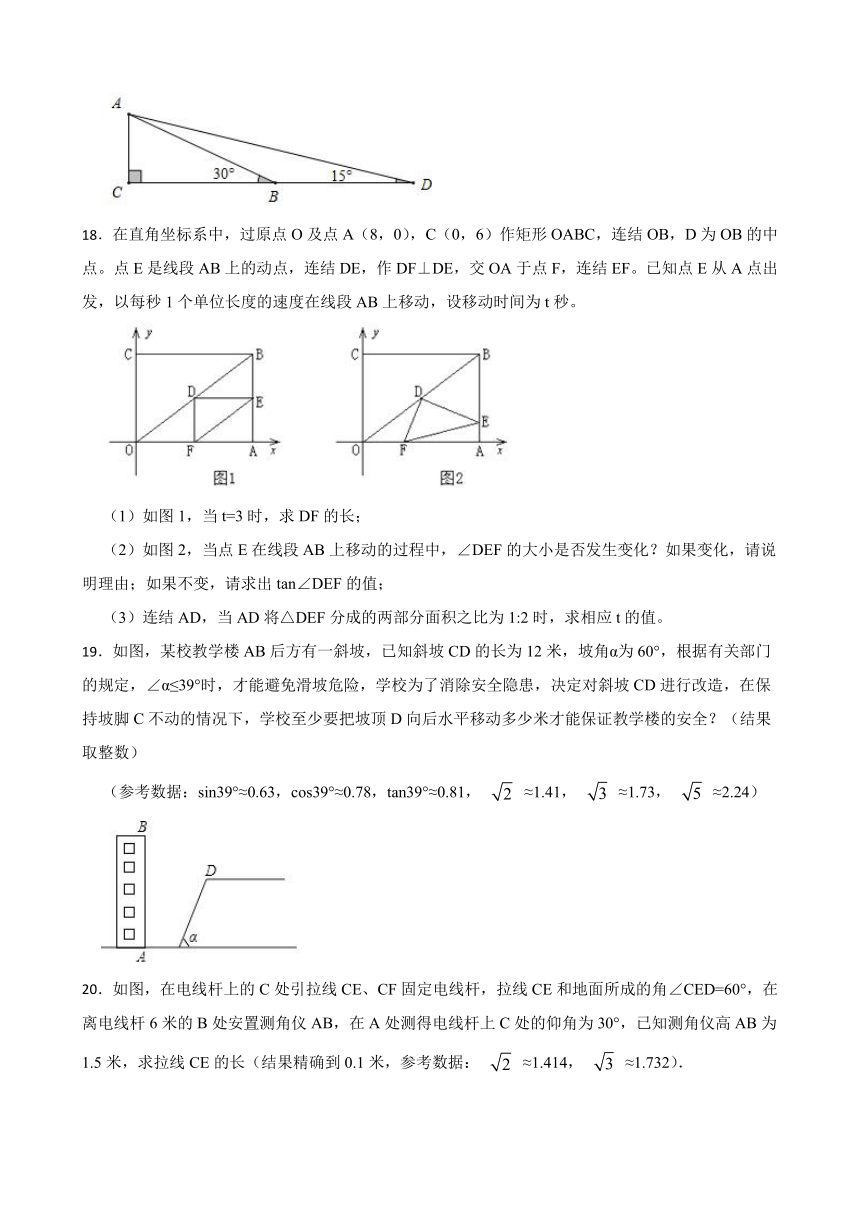
18.在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。
(1)如图1,当t=3时,求DF的长;
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;
(3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。
19.如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81, ≈1.41, ≈1.73, ≈2.24)
20.如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据: ≈1.414, ≈1.732).
四、综合题
21.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点D是的中点,连接OD,交AC于点E,作BFCD,交DO的延长线于点F.
(1)求证:四边形BCDF是平行四边形.
(2)若AC=8,连接BD,tan∠DBF= ,求直径AB的长及四边形ABCD的周长.
答案解析部分
1.【答案】C
【解析】【解答】解:∵,
∴.
故答案为:C.
【分析】利用解直角三角形的方法可得。
2.【答案】C
【解析】【解答】因为在△ABC中,∠C=90°,AC=1,BC=2,根据勾股定理可得: ,根据余弦三角函数的定义可得: ,故答案为:C.
【分析】根据勾股定理算出AB的长,根据余弦三角函数的定义可得:cosA的值。
3.【答案】A
【解析】【解答】解:60°+20°=80°.
由北偏西20°转向北偏东60°,需要向右转.
故答案为:A.
【分析】将射线BC绕点B顺时针旋转80°可使A、B、C三点共线,据此解答即可.
4.【答案】A
【解析】【解答】解:由作图知PQ为线段AB的垂直平分线,
∴AD=BD,
∵ ,
∴CD=2,AD=6,
∴AC= = = .
故答案为:A
【分析】由 , ,求出CD=2,AD=6,再根据勾股定理即可得出答案.
5.【答案】B
【解析】【解答】∵此船从上午8时的B处向东航行2小时后到C处,
且从C观测处到灯塔A在它的正南方向,
∴∠BCA=90°,
∵ 处在 处的南偏东60°且距离为72海里
∴∠ABC=30°,AB=72海里,
∴在Rt△ABC中,
∵∠A=60°,
∴ =sin60°,
∴ 海里,
速度为 海里/小时,
故答案为:B.
【分析】先画图,在构造直角三角形,利用勾股定理求出8时到10时航行的距离,在求速度即可解答。
6.【答案】B
【解析】【解答】解:过点B作BF⊥x轴于F,过点D作DE⊥x轴于E
∵ , 点横坐标为
∴AF=1-(-1)=2
∵
∴BF=AF·tan∠BAO=
∴点B的坐标为(-1, )
∵四边形ABCD为矩形
∴∠BAD=90°
∴∠DAE=180°-∠BAO-∠BAD=30°
∴sin∠DAE=
设DE= ,则AE=3a
∴OE=AO-AE=3a+1
∴点D的坐标为(3a+1, )
∵四边形ABCD为矩形
∴BC可看作由AD平移得到
∵点A到点B的平移方式为:先向左平移2个单位,再向上平移 个单位
∴AD到BC的平移方式为:先向左平移2个单位,再向上平移 个单位
∴点C的坐标为(3a-1, + )
将C、D的坐标代入反比例函数解析式中,得
①-②并整理,得
4a=2
解得:a=
将a= 代入②,解得:k=
故答案为:B.
【分析】过点B作BF⊥x轴于F,过点D作DE⊥x轴于E,由 且 , 点横坐标为 , 可得AF=2,根据锐角三角函数可得BF=AF·tan∠BAO,设DE=m,则AE=,故可得点D(,m)由AD∥BC且AD=BC可得点C坐标(-1+,)由点C、D在反比例函数图象上,可得k=点C横纵坐标的乘积=点D横纵坐标的乘积,即可得m的值,即可得k的值.
7.【答案】D
【解析】【解答】解: 如图,过点C作CD⊥AB,垂足为D,
船以每小时36海里的速度向正北行驶了40分钟,所以AC=36×=24(海里).
在Rt△ACD中,AC=24海里,∠A=45°,
所以CD=AC×sin45°=24×=(海里).
因为∠ACB=180°-75°=105°,∠A=45°,
所以∠DCB=60°.
在Rt△BCD中,CD=海里,∠BCD=60°,
∴(海里).
故答案为:D.
【分析】 要求BC的长,构造直角三角形,并且含有特殊角,为此过C作AB的垂线CD. 在Rt△ACD中求CD,在Rt△BCD中再求BC,即可解答.
8.【答案】C
【解析】【解答】解:由作法得AE垂直平分CD,
∴∠AED=90°,CE=DE,
∵四边形ABCD为菱形,
∴AD=2DE,
∴∠DAE=30°,∠D=60°,
∴∠ABC=60°,所以A选项的说法正确;
∵AB=2DE,
∴S△ABE=2S△ADE,所以B选项的说法正确;
作EH⊥BC于H,如图,
若AB=4,在Rt△ECH中,∵∠ECH=60°,∴CH=CE=1,EH=,
在Rt△BEH中,利用勾股定理得:BE=,所以C选项的说法错误;
sin∠CBE=,所以D选项的说法正确.
故答案为:C.
【分析】由作法得AE垂直平分CD,则∠AED=90°,CE=DE,根据含30°角的直角三角形的边之间的关系的逆用得出∠DAE=30°,进而根据三角形的内角和得出∠D=60°,根据菱形的对角相等得出∠ABC=60°;利用平行线间的距离相等,由同高三角形的面积之间的关系等于两底之间的关系,由AB=2DE得到S△ABE=2S△ADE;作EH⊥BC于H,如图,若AB=4,根据含30°直角三角形的边之间的关系计算出CH,EH,进而根据勾股定理算出BE的长,最后根据锐角三角函数的定义,由sin∠CBE=即可算出答案 sin∠CBE 的值,从而一一判断得出答案。
9.【答案】A
【解析】【解答】解:如图所示,过点作于点,
∵,,
∴,
在中,,
∴,
∵设开往码头、的游船速度分别为、,回到、所用时间相等,
∴,
故答案为:A.
【分析】过点C作CD⊥AB于点D,根据含30°角的直角三角形的性质可得CD=AC=2,由勾股定理可得BC的值,由题意可得v1:v2=AC:CB,据此求解.
10.【答案】B
【解析】【解答】解:如图,过点A作HQ⊥l1于点H,交l2于点Q,
∴∠BHA=∠AQD=90°
∵正方形ABCD,
∴AB=AD=a,∠BAD=90°
∴∠2+∠DAQ=90°,∠ADQ+∠DAQ=90°,
∴∠2=∠ADQ=α
在Rt△ADQ中,
AQ=ADsin∠ADQ=asinα;
在Rt△ABH中,
AH=ABcos∠ADQ=acosα;
∴两条平行线间的距离为AH+AQ=asinα+acosα.
故答案为:B.
【分析】过点A作HQ⊥l1于点H,交l2于点Q,利用垂直的定义可得到∠BHA=∠AQD=90°;再利用正方形的性质可以推出AB=AD=a,∠BAD=90°,同时可证得∠2=∠ADQ=α;然后利用解直角三角形分别表示出AQ,AH,从而可求出两条平行线之间的距离。
11.【答案】
【解析】【解答】解:如图所示:在A点处观察B点的仰角为,即,
∵,
∴,
∴在B点处观察A点的俯角为,
故答案为:.
【分析】顶点在x轴上,根据平行线的性质得出,即可得出答案。
12.【答案】6
【解析】【解答】解:如图,过A作AE⊥BC,过D作DF⊥BC,
AE=DF=1米,AD=EF=3米,
∵坡度===,
∴BE=CF=1.5米,
∴BC=BE+EF+CF=1.5+3+1.5=6米.
故答案为6.
【分析】过A作AE⊥BC,过D作DF⊥BC,先根据坡度可求出BE=CF=1.5米,再利用BC=BE+EF+CF计算即可。
13.【答案】10
【解析】【解答】解:原式=9﹣2 +1+2 =10,
故答案为:10
【分析】原式利用负整数指数幂法则,绝对值的代数意义,特殊角的三角函数值计算即可得到结果.
14.【答案】
【解析】【解答】∵AE⊥BC,AF⊥DC,
∴
又∵AB∥DC,
∴ .
又∵ ,
∴ .
∵ ,
∴ ,即 .
又∵ ∠ B=∠D,所以 , .
由题,AF=4,AE=6,
则根据勾股定理,易得 , ,
∴ .
所以本题的正确答案为 .
【分析】可作辅助线EG⊥AF交AF于点G,可发现∠EAF=∠B,由此可根据余弦值于AE长度得到AB与BE的长度;再根据∠D=∠B可得△ADF与△ABE相似,那么根据相似比可得到AD,DF的长度,平行四边形对边相等,从而得到CF的长度。
15.【答案】
【解析】【解答】解:原式= × .
故答案为: .
【分析】直接利用特殊角的三角函数值代入求出答案.
16.【答案】解:过点A作射线AO交☉O于点D,连接CD.∵AD为直径,∴AD=12,∠ACD=90°.∵∠B=60°,∴∠D=60°.在Rt△ADC中,∵sin∠D= ,∴AC=AD·sin60°=12× = .
【解析】【分析】抓住已知条件∠B=60°,添加辅助线,作直径AD,连接CD,利用同弧所对的圆周角相等得出∠B=∠D=60°,在Rt△ADC中,利用锐角三角函数的定义求出AC的长即可。
17.【答案】解:在Rt△ACB中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°,
设AC=BC=1,则AB=BD= ,
∴tan22.5°= = .
【解析】【分析】在等腰直角△ABC中,延长CB至点D,使得AB= BD,则∠BAD=∠D.设AC= 1,求出CD,即可求解.
18.【答案】(1)解:当t=3时,如图1,点E为AB中点.
∵点D为OB中点,
∴DE//OA,DE=OA=4,
∵OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°
∴四边形DFAE是矩形,
∴DF=AE=3.
(2)解: ∵∠DEF大小不变,如图2,
过D作DM⊥OA,DN⊥AB,垂足分别是M、N,
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM//AB,DN//OA,
∴,,
∵点D为OB中点,
∴M、N分别是OA、AB中点,
∴DM=AB=3,DN=OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN.
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE
∴,
∵∠EDF=90°,
∴tan∠DEF=
(3)解:过D作DM⊥OA,DN⊥AB。垂足分别是M,N.
若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
①当点E到达中点之前时.
NE=3-t,由△DMF∽△DNE得
MF=(3-t).
∴AF=4+MF=-t+.
∵点为EF的三等分点。
∴(.t).
由点A(8,0),D(4,3)得直线AD解析式为y=-χ+6.
(.t)代入,得t=.
②当点E越过中点之后.
NE=t-3,由△DMF~△DNE得MF=(t-3).
∴AF=4-MF=-+.
∵点为EF的三等分点.
∴(.).
代入直线AD解析式y=-χ+6.
得t=.
【解析】【分析】(1)当t=3时,如图1,点E、D分别为AB、OB中点,得出DE//OA,DE=OA=4,根据OA⊥AB得出DE⊥AB,从而得出四边形DFAE是矩形,根据矩形性质求出DF=AE=3.
(2)如图2,过D作DM⊥OA,DN⊥AB,垂足分别是M、N,四边形OABC、DMAN都是矩形,由平行得出,,由D、M、N是中点又可以得出条件判断△DMF∽△DNE,从而得出tan∠DEF=。
(3)过D作DM⊥OA,DN⊥AB。垂足分别是M,N;若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
分点E到达中点之前或越过中点之后来讨论,得出 NE,由△DMF∽△DNE得 MF和AF的长度, 再算出直线AD的解析式,由点G为EF的三等分点得出G点坐标将其代入AD直线方程求出t值。
19.【答案】解:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
∵CD=12米,∠DCE=60°,
∴DE=CD sin60°=12× =6 米,CE=CD cos60°=12× =6米.
∵DE⊥AC,D′E′⊥AC,DD′∥CE′,
∴四边形DEE′D′是矩形,
∴DE=D′E′=6 米.
∵∠D′CE′=39°,
∴CE′= ≈ ≈12.8,
∴EE′=CE′﹣CE=12.8﹣6=6.8≈7(米).
答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.
【解析】【分析】假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,根据锐角三角函数的定义求出DE、CE、CE′的长,进而可得出结论.
20.【答案】解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH= ,
∴CH=AH tan∠CAH,
∴CH=AH tan∠CAH=6tan30°=6× =2 ,
∵DH=1.5,
∴CD=2 +1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED= ,
∴CE= =4+ ≈5.7(米),
答:拉线CE的长约为5.7米
【解析】【分析】过点A作AH⊥CD,垂足为H,在Rt△ACH中求出CH,在Rt△ECD中,再求出EC即可.
21.【答案】(1)证明:∵AB是⊙O的直径,
∴∠C=90°,
∵点D是的中点,
∴DO垂直平分AC,且AD=DC,
∴CA⊥DF,AE=EC,
∴∠AEO=90°,
∴,
∵,
∴四边形BCDE是平行四边形;
(2)∵,
∴∠DBF=∠CDB,
又∵根据圆周角定理有∠CDB=∠BAC,
∴∠DBF=∠BAC,
即tan∠BAC=,
∵AC=8,
∴CB=6,
则在Rt△ACB中,利用勾股定理可得AB=10,即AO=5=OD,
∵AE=EC=AC,
∴AE=EC=4,
在Rt△AEO中,利用勾股定理得OE=3,
∴DE=OD-OE=5-3=2,
在Rt△AED中,利用勾股定理,得AD=2,则有CD=2,
∴四边形ABCD的周长=AB+BC+CD+AD=10+6+2+2=16+.
【解析】【分析】 (1)根据圆周角定理可得∠C=90°,由题意可得DO垂直平分AC,且AD=DC,则CA⊥DF,AE=EC,然后根据平行四边形的判定定理进行证明;
(2)根据平行线的性质可得∠DBF=∠CDB,根据圆周角定理有∠CDB=∠BAC,则∠DBF=∠BAC,结合三角函数的概念可得CB=6,利用勾股定理求出AB=10,则AO=5=OD,AE=EC=4,利用勾股定理求出OE、AD,进而得到DE、CD,据此不难求出四边形ABCD的周长.
一、单选题
1.如图,小明在数学兴趣小组探究活动中要测量河的宽度,他和同学在河对岸选定一点A,再在河的这一边选定点P和点B,使.利用工具测得米,,根据测量数据可计算得到小河宽度为( )
A.米 B.米 C.米 D.米
2.在△ABC中,∠C=90°,AC=1,BC=2,则 cos A的值是( )
A. B. C. D.
3.如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.右转80° B.左转80° C.右转100° D.左转100°
4.如图,在 中, ,按以下步骤作图:①分别以点 为圆心,大于 的长为半径作弧,两弧交于点 ;②作直线 交边 于点D,连接 ,若 ,则 的长为( )
A. B.6 C.4 D.
5.一船向东航行,上午8时到达 处,观测到有一灯塔在它的南偏东60°且距离为72海里的 处,上午10时到达 处,此时观测到灯塔在它的正南方向,则这艘船航行的速度为( )
A.18海里/小时 B. 海里/小时
C.36海里/小时 D. 海里/小时
6.如图,在平面直角坐标系中,反比例函数 ( , )的图象经过矩形 的顶点 、 , ,且 , 点横坐标为 ,则 的值为( )
A. B. C. D.
7.如图,一船以每小时36海里的速度向正北航行到A处,发现它的东北方向有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在它的北偏东75°方向,则此时船与灯塔的距离为( )
A.24 B. C. D.
8.如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于 CD的长为半径作弧,两弧相交于M、N两点;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE.则下列说法错误的是( )
A.∠ABC=60° B.S△ABE=2S△ADE
C.若AB=4,则BE= D.sin∠CBE=
9.如图,在一笔直的沿湖道路l上有、两个游船码头,观光岛屿在码头北偏东的方向,在码头北偏西的方向,.游客小张准备从观光岛屿乘船沿回到码头或沿回到码头,设开往码头、的游船速度分别为、,若回到、所用时间相等,则( )
A. B. C.4 D.6
10.如图是墙壁上在l1,l2两条平行线间的边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为α,则两条平行线间的距离为( )
A.2asinα B.asinα+acosα C.2acosα D.asinα-acosα
二、填空题
11.如果在A点处观察B点的仰角为,那么在B点处观察A点的俯角为 (用含的式子表示)
12.如图,一段铁路路基的横断面为等腰梯形,路基的上底宽AD为3米,路基高为1米,斜坡AB的坡度,那么路基的下底宽BC是 米.
13.计算:(﹣ )﹣2﹣|1﹣ |+4cos45°= .
14.如图,平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=6,AF=4,cos∠EAF= ,则CF= .
15.计算sin60°cos60°的值为 .
三、解答题
16.如图, 内接于⊙ .若⊙ 的半径为6, ,求 的长.
17.构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)
18.在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。
(1)如图1,当t=3时,求DF的长;
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;
(3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。
19.如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81, ≈1.41, ≈1.73, ≈2.24)
20.如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据: ≈1.414, ≈1.732).
四、综合题
21.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点D是的中点,连接OD,交AC于点E,作BFCD,交DO的延长线于点F.
(1)求证:四边形BCDF是平行四边形.
(2)若AC=8,连接BD,tan∠DBF= ,求直径AB的长及四边形ABCD的周长.
答案解析部分
1.【答案】C
【解析】【解答】解:∵,
∴.
故答案为:C.
【分析】利用解直角三角形的方法可得。
2.【答案】C
【解析】【解答】因为在△ABC中,∠C=90°,AC=1,BC=2,根据勾股定理可得: ,根据余弦三角函数的定义可得: ,故答案为:C.
【分析】根据勾股定理算出AB的长,根据余弦三角函数的定义可得:cosA的值。
3.【答案】A
【解析】【解答】解:60°+20°=80°.
由北偏西20°转向北偏东60°,需要向右转.
故答案为:A.
【分析】将射线BC绕点B顺时针旋转80°可使A、B、C三点共线,据此解答即可.
4.【答案】A
【解析】【解答】解:由作图知PQ为线段AB的垂直平分线,
∴AD=BD,
∵ ,
∴CD=2,AD=6,
∴AC= = = .
故答案为:A
【分析】由 , ,求出CD=2,AD=6,再根据勾股定理即可得出答案.
5.【答案】B
【解析】【解答】∵此船从上午8时的B处向东航行2小时后到C处,
且从C观测处到灯塔A在它的正南方向,
∴∠BCA=90°,
∵ 处在 处的南偏东60°且距离为72海里
∴∠ABC=30°,AB=72海里,
∴在Rt△ABC中,
∵∠A=60°,
∴ =sin60°,
∴ 海里,
速度为 海里/小时,
故答案为:B.
【分析】先画图,在构造直角三角形,利用勾股定理求出8时到10时航行的距离,在求速度即可解答。
6.【答案】B
【解析】【解答】解:过点B作BF⊥x轴于F,过点D作DE⊥x轴于E
∵ , 点横坐标为
∴AF=1-(-1)=2
∵
∴BF=AF·tan∠BAO=
∴点B的坐标为(-1, )
∵四边形ABCD为矩形
∴∠BAD=90°
∴∠DAE=180°-∠BAO-∠BAD=30°
∴sin∠DAE=
设DE= ,则AE=3a
∴OE=AO-AE=3a+1
∴点D的坐标为(3a+1, )
∵四边形ABCD为矩形
∴BC可看作由AD平移得到
∵点A到点B的平移方式为:先向左平移2个单位,再向上平移 个单位
∴AD到BC的平移方式为:先向左平移2个单位,再向上平移 个单位
∴点C的坐标为(3a-1, + )
将C、D的坐标代入反比例函数解析式中,得
①-②并整理,得
4a=2
解得:a=
将a= 代入②,解得:k=
故答案为:B.
【分析】过点B作BF⊥x轴于F,过点D作DE⊥x轴于E,由 且 , 点横坐标为 , 可得AF=2,根据锐角三角函数可得BF=AF·tan∠BAO,设DE=m,则AE=,故可得点D(,m)由AD∥BC且AD=BC可得点C坐标(-1+,)由点C、D在反比例函数图象上,可得k=点C横纵坐标的乘积=点D横纵坐标的乘积,即可得m的值,即可得k的值.
7.【答案】D
【解析】【解答】解: 如图,过点C作CD⊥AB,垂足为D,
船以每小时36海里的速度向正北行驶了40分钟,所以AC=36×=24(海里).
在Rt△ACD中,AC=24海里,∠A=45°,
所以CD=AC×sin45°=24×=(海里).
因为∠ACB=180°-75°=105°,∠A=45°,
所以∠DCB=60°.
在Rt△BCD中,CD=海里,∠BCD=60°,
∴(海里).
故答案为:D.
【分析】 要求BC的长,构造直角三角形,并且含有特殊角,为此过C作AB的垂线CD. 在Rt△ACD中求CD,在Rt△BCD中再求BC,即可解答.
8.【答案】C
【解析】【解答】解:由作法得AE垂直平分CD,
∴∠AED=90°,CE=DE,
∵四边形ABCD为菱形,
∴AD=2DE,
∴∠DAE=30°,∠D=60°,
∴∠ABC=60°,所以A选项的说法正确;
∵AB=2DE,
∴S△ABE=2S△ADE,所以B选项的说法正确;
作EH⊥BC于H,如图,
若AB=4,在Rt△ECH中,∵∠ECH=60°,∴CH=CE=1,EH=,
在Rt△BEH中,利用勾股定理得:BE=,所以C选项的说法错误;
sin∠CBE=,所以D选项的说法正确.
故答案为:C.
【分析】由作法得AE垂直平分CD,则∠AED=90°,CE=DE,根据含30°角的直角三角形的边之间的关系的逆用得出∠DAE=30°,进而根据三角形的内角和得出∠D=60°,根据菱形的对角相等得出∠ABC=60°;利用平行线间的距离相等,由同高三角形的面积之间的关系等于两底之间的关系,由AB=2DE得到S△ABE=2S△ADE;作EH⊥BC于H,如图,若AB=4,根据含30°直角三角形的边之间的关系计算出CH,EH,进而根据勾股定理算出BE的长,最后根据锐角三角函数的定义,由sin∠CBE=即可算出答案 sin∠CBE 的值,从而一一判断得出答案。
9.【答案】A
【解析】【解答】解:如图所示,过点作于点,
∵,,
∴,
在中,,
∴,
∵设开往码头、的游船速度分别为、,回到、所用时间相等,
∴,
故答案为:A.
【分析】过点C作CD⊥AB于点D,根据含30°角的直角三角形的性质可得CD=AC=2,由勾股定理可得BC的值,由题意可得v1:v2=AC:CB,据此求解.
10.【答案】B
【解析】【解答】解:如图,过点A作HQ⊥l1于点H,交l2于点Q,
∴∠BHA=∠AQD=90°
∵正方形ABCD,
∴AB=AD=a,∠BAD=90°
∴∠2+∠DAQ=90°,∠ADQ+∠DAQ=90°,
∴∠2=∠ADQ=α
在Rt△ADQ中,
AQ=ADsin∠ADQ=asinα;
在Rt△ABH中,
AH=ABcos∠ADQ=acosα;
∴两条平行线间的距离为AH+AQ=asinα+acosα.
故答案为:B.
【分析】过点A作HQ⊥l1于点H,交l2于点Q,利用垂直的定义可得到∠BHA=∠AQD=90°;再利用正方形的性质可以推出AB=AD=a,∠BAD=90°,同时可证得∠2=∠ADQ=α;然后利用解直角三角形分别表示出AQ,AH,从而可求出两条平行线之间的距离。
11.【答案】
【解析】【解答】解:如图所示:在A点处观察B点的仰角为,即,
∵,
∴,
∴在B点处观察A点的俯角为,
故答案为:.
【分析】顶点在x轴上,根据平行线的性质得出,即可得出答案。
12.【答案】6
【解析】【解答】解:如图,过A作AE⊥BC,过D作DF⊥BC,
AE=DF=1米,AD=EF=3米,
∵坡度===,
∴BE=CF=1.5米,
∴BC=BE+EF+CF=1.5+3+1.5=6米.
故答案为6.
【分析】过A作AE⊥BC,过D作DF⊥BC,先根据坡度可求出BE=CF=1.5米,再利用BC=BE+EF+CF计算即可。
13.【答案】10
【解析】【解答】解:原式=9﹣2 +1+2 =10,
故答案为:10
【分析】原式利用负整数指数幂法则,绝对值的代数意义,特殊角的三角函数值计算即可得到结果.
14.【答案】
【解析】【解答】∵AE⊥BC,AF⊥DC,
∴
又∵AB∥DC,
∴ .
又∵ ,
∴ .
∵ ,
∴ ,即 .
又∵ ∠ B=∠D,所以 , .
由题,AF=4,AE=6,
则根据勾股定理,易得 , ,
∴ .
所以本题的正确答案为 .
【分析】可作辅助线EG⊥AF交AF于点G,可发现∠EAF=∠B,由此可根据余弦值于AE长度得到AB与BE的长度;再根据∠D=∠B可得△ADF与△ABE相似,那么根据相似比可得到AD,DF的长度,平行四边形对边相等,从而得到CF的长度。
15.【答案】
【解析】【解答】解:原式= × .
故答案为: .
【分析】直接利用特殊角的三角函数值代入求出答案.
16.【答案】解:过点A作射线AO交☉O于点D,连接CD.∵AD为直径,∴AD=12,∠ACD=90°.∵∠B=60°,∴∠D=60°.在Rt△ADC中,∵sin∠D= ,∴AC=AD·sin60°=12× = .
【解析】【分析】抓住已知条件∠B=60°,添加辅助线,作直径AD,连接CD,利用同弧所对的圆周角相等得出∠B=∠D=60°,在Rt△ADC中,利用锐角三角函数的定义求出AC的长即可。
17.【答案】解:在Rt△ACB中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°,
设AC=BC=1,则AB=BD= ,
∴tan22.5°= = .
【解析】【分析】在等腰直角△ABC中,延长CB至点D,使得AB= BD,则∠BAD=∠D.设AC= 1,求出CD,即可求解.
18.【答案】(1)解:当t=3时,如图1,点E为AB中点.
∵点D为OB中点,
∴DE//OA,DE=OA=4,
∵OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°
∴四边形DFAE是矩形,
∴DF=AE=3.
(2)解: ∵∠DEF大小不变,如图2,
过D作DM⊥OA,DN⊥AB,垂足分别是M、N,
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM//AB,DN//OA,
∴,,
∵点D为OB中点,
∴M、N分别是OA、AB中点,
∴DM=AB=3,DN=OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN.
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE
∴,
∵∠EDF=90°,
∴tan∠DEF=
(3)解:过D作DM⊥OA,DN⊥AB。垂足分别是M,N.
若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
①当点E到达中点之前时.
NE=3-t,由△DMF∽△DNE得
MF=(3-t).
∴AF=4+MF=-t+.
∵点为EF的三等分点。
∴(.t).
由点A(8,0),D(4,3)得直线AD解析式为y=-χ+6.
(.t)代入,得t=.
②当点E越过中点之后.
NE=t-3,由△DMF~△DNE得MF=(t-3).
∴AF=4-MF=-+.
∵点为EF的三等分点.
∴(.).
代入直线AD解析式y=-χ+6.
得t=.
【解析】【分析】(1)当t=3时,如图1,点E、D分别为AB、OB中点,得出DE//OA,DE=OA=4,根据OA⊥AB得出DE⊥AB,从而得出四边形DFAE是矩形,根据矩形性质求出DF=AE=3.
(2)如图2,过D作DM⊥OA,DN⊥AB,垂足分别是M、N,四边形OABC、DMAN都是矩形,由平行得出,,由D、M、N是中点又可以得出条件判断△DMF∽△DNE,从而得出tan∠DEF=。
(3)过D作DM⊥OA,DN⊥AB。垂足分别是M,N;若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
分点E到达中点之前或越过中点之后来讨论,得出 NE,由△DMF∽△DNE得 MF和AF的长度, 再算出直线AD的解析式,由点G为EF的三等分点得出G点坐标将其代入AD直线方程求出t值。
19.【答案】解:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
∵CD=12米,∠DCE=60°,
∴DE=CD sin60°=12× =6 米,CE=CD cos60°=12× =6米.
∵DE⊥AC,D′E′⊥AC,DD′∥CE′,
∴四边形DEE′D′是矩形,
∴DE=D′E′=6 米.
∵∠D′CE′=39°,
∴CE′= ≈ ≈12.8,
∴EE′=CE′﹣CE=12.8﹣6=6.8≈7(米).
答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.
【解析】【分析】假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,根据锐角三角函数的定义求出DE、CE、CE′的长,进而可得出结论.
20.【答案】解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH= ,
∴CH=AH tan∠CAH,
∴CH=AH tan∠CAH=6tan30°=6× =2 ,
∵DH=1.5,
∴CD=2 +1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED= ,
∴CE= =4+ ≈5.7(米),
答:拉线CE的长约为5.7米
【解析】【分析】过点A作AH⊥CD,垂足为H,在Rt△ACH中求出CH,在Rt△ECD中,再求出EC即可.
21.【答案】(1)证明:∵AB是⊙O的直径,
∴∠C=90°,
∵点D是的中点,
∴DO垂直平分AC,且AD=DC,
∴CA⊥DF,AE=EC,
∴∠AEO=90°,
∴,
∵,
∴四边形BCDE是平行四边形;
(2)∵,
∴∠DBF=∠CDB,
又∵根据圆周角定理有∠CDB=∠BAC,
∴∠DBF=∠BAC,
即tan∠BAC=,
∵AC=8,
∴CB=6,
则在Rt△ACB中,利用勾股定理可得AB=10,即AO=5=OD,
∵AE=EC=AC,
∴AE=EC=4,
在Rt△AEO中,利用勾股定理得OE=3,
∴DE=OD-OE=5-3=2,
在Rt△AED中,利用勾股定理,得AD=2,则有CD=2,
∴四边形ABCD的周长=AB+BC+CD+AD=10+6+2+2=16+.
【解析】【分析】 (1)根据圆周角定理可得∠C=90°,由题意可得DO垂直平分AC,且AD=DC,则CA⊥DF,AE=EC,然后根据平行四边形的判定定理进行证明;
(2)根据平行线的性质可得∠DBF=∠CDB,根据圆周角定理有∠CDB=∠BAC,则∠DBF=∠BAC,结合三角函数的概念可得CB=6,利用勾股定理求出AB=10,则AO=5=OD,AE=EC=4,利用勾股定理求出OE、AD,进而得到DE、CD,据此不难求出四边形ABCD的周长.
