二次函数复习

课件13张PPT。二 次 函 数 复习(一)舟山南海实验学校 张宏政西堠门大桥著名数学家华罗庚： 数缺形时少直观，
形少数时难入微。
数形结合百般好，
隔离分家万事休!
数缺形时少直观，
形少数时难入微。
数形结合百般好，
隔离分家万事休!
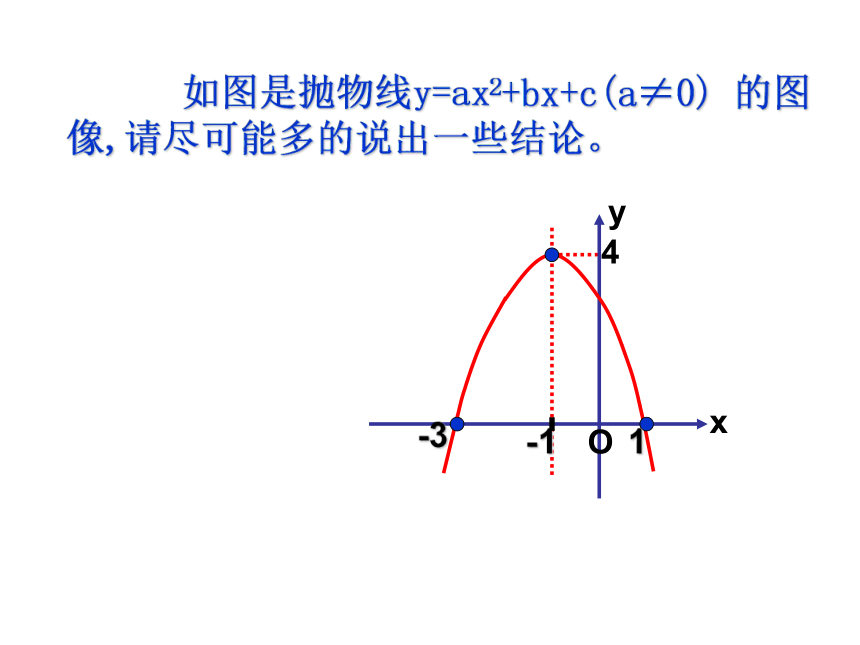
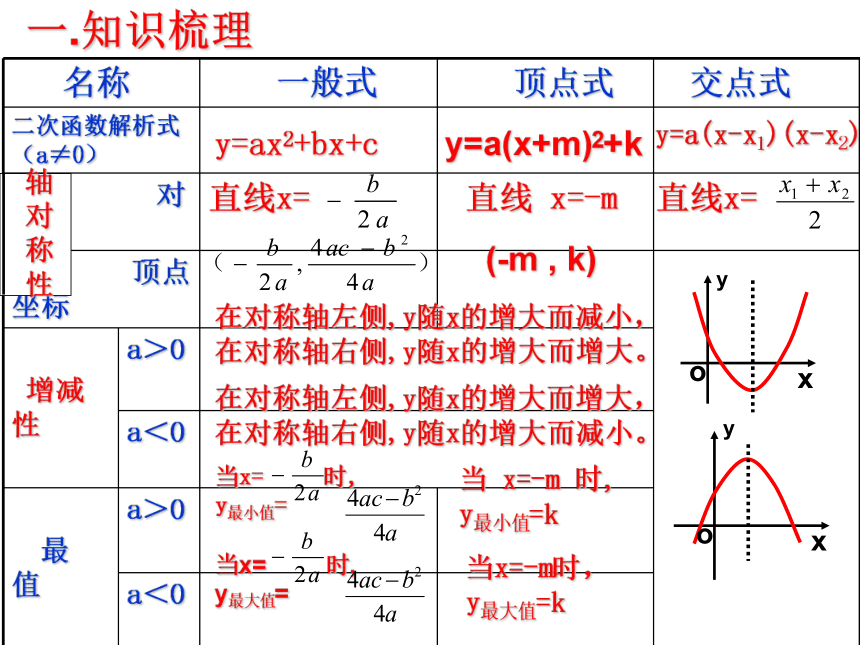
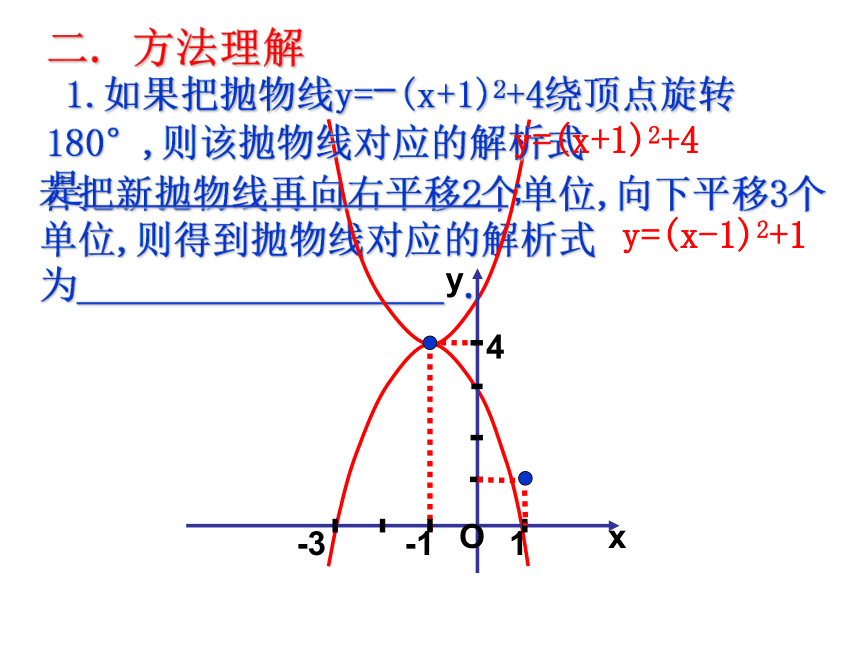
如图是抛物线y=ax2+bx+c(a≠0) 的图像,请尽可能多的说出一些结论。yxO-11-34y=a(x+m)2+ky=ax2+bx+cy=a(x-x1)(x-x2)直线 x=-m直线x=直线x=(-m , k)当 x=-m 时, y最小值=k当x= 时, y最小值=当x=-m时， y最大值=k当x= 时, y最大值=yxooyx在对称轴左侧,y随x的增大而减小，在对称轴右侧,y随x的增大而增大。在对称轴左侧,y随x的增大而增大， 在对称轴右侧,y随x的增大而减小。一.知识梳理轴 对称性若把新抛物线再向右平移2个单位,向下平移3个单位,则得到抛物线对应的解析式为 .二. 方法理解 1.如果把抛物线y=-(x+1)2+4绕顶点旋转180°,则该抛物线对应的解析式是 ;yxO-1 14-3y=(x+1)2+4y=(x-1)2+1二. 方法理解yxO-1 14-3y=-(x+1)2+42. 问题1. 结合图像思考:
方程-(x+1)2+4=1有几个实数解?011x1x2 问题2. 结合图像思考： 当m为何值时, 方程-(x+1)2+4=m ①有两个不相等的实数根; ②有两个相等的实数根; ③没有实数根?yxO-1 14-3y=-(x+1)2+4y=mm1yxO-1 14-3问题(3) 若直线y1=kx+m与抛物线y2=ax2+bx+c交于A(1,0),B(-1,4)两点. 观察图像填空：
(1)方程ax2+bx+c=kx+m 的解为 . (2)不等式ax2+bx+c＞kx+m 的解为 . (3)不等式ax2+bx+c＜kx+m 的解为 . ABx1=-1,x2=1-1＜x＜1方程,不等式(数) 函数(形)x＜-1或x＞1转化图像解法 2.若一元二次方程ax2+bx+c=0的系数满足a + b + c＜0, a – b + c=2,则该方程( )
A. 必有两个不相等的实数根； B. 必有两个相等的实数根； C. 必无实数根； D. 无法确定. 三、巩固反馈
1. 方程 实数解的个数为( )
A. 3个 B. 2个 C. 1个 D. 0个CA 按右图的流程,输入一个数据x,由y与x的解析式就输出一个数据y,要使任意一组在20～100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求：
(1)新数据都在60～100(含60和100)之间；
(2)新数据的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大.
若按解析式y=a(x+m)2＋k (a>0) 将数据进行变换,请写出一个满足上述要求的这种解析式.四. 拓展提高开始y与x的解析式(a＜0)(2)新数据的大小关系与原数据之间的大小关系相反,即原数据越大的对应的新数据越小.五. 分享收获一个核心: 数形结合思想(用数表达,用形释义);
二项性质: 轴对称性(图像特征),增减性(变化规律);
三种表示:
y=ax2+bx+c=a(x+m)2+k=a(x-x1)(x-x2) (a≠0);
四点注意：
① a的意义… ②二次函数的函数值大小…
③抛物线的平移…
④方程,不等式(数)的问题…祝同学们学业进步,收获多多！
再 见 !浙江舟山南海实验学校初中部 张宏政
联系电话: (0580)2091115, e-mail: nhxx_zhz@126.com基础 + 方法 = 能力!