6.2平面直角坐标系(1)

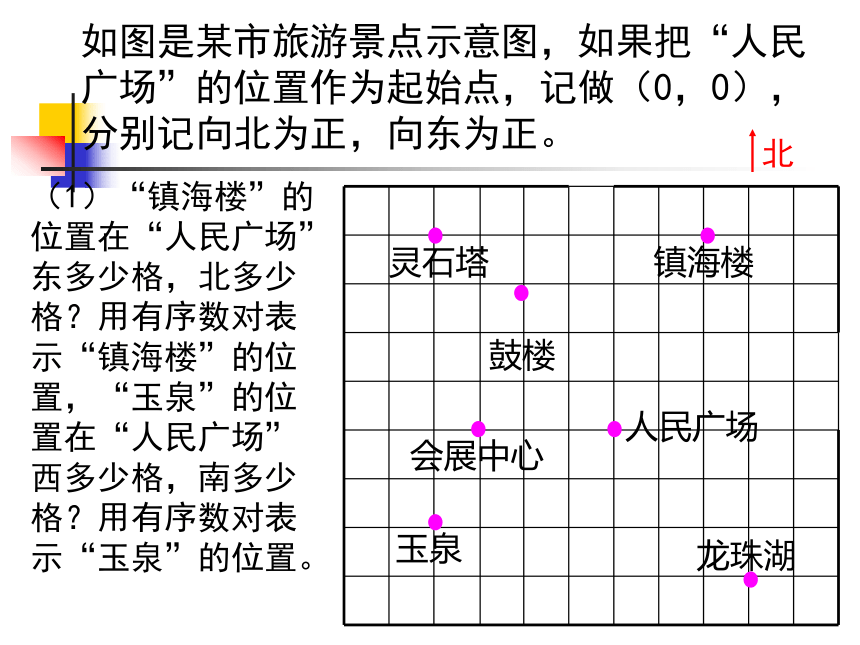
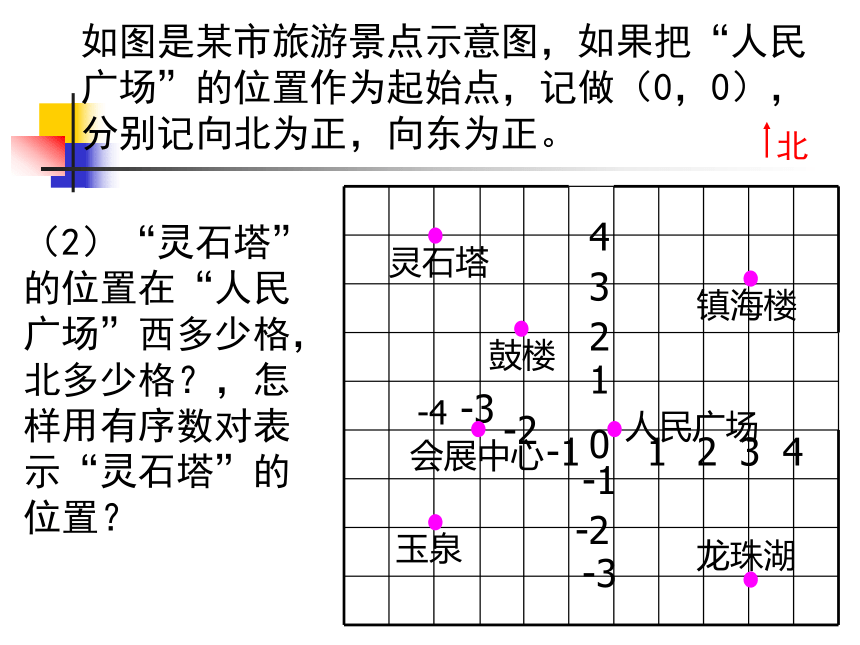
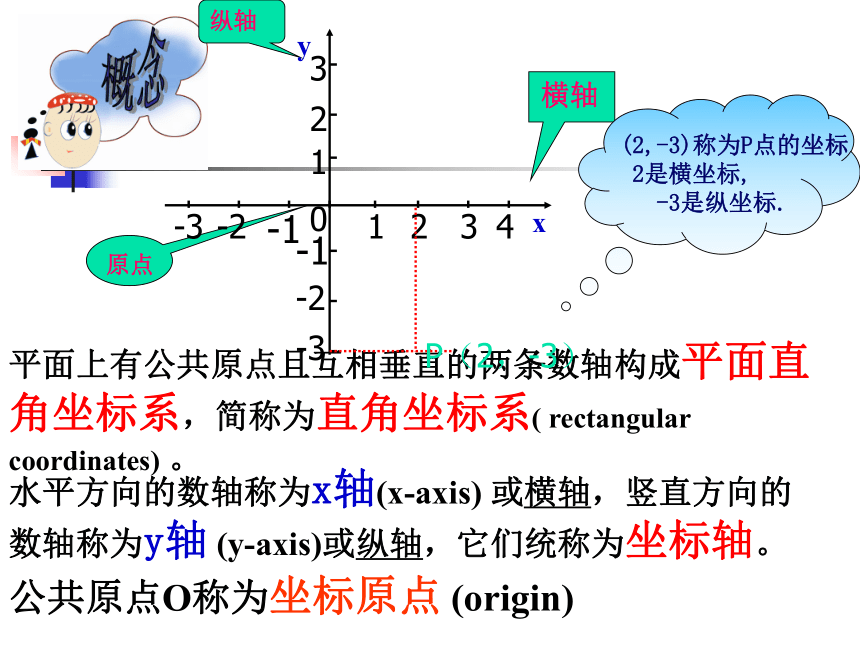
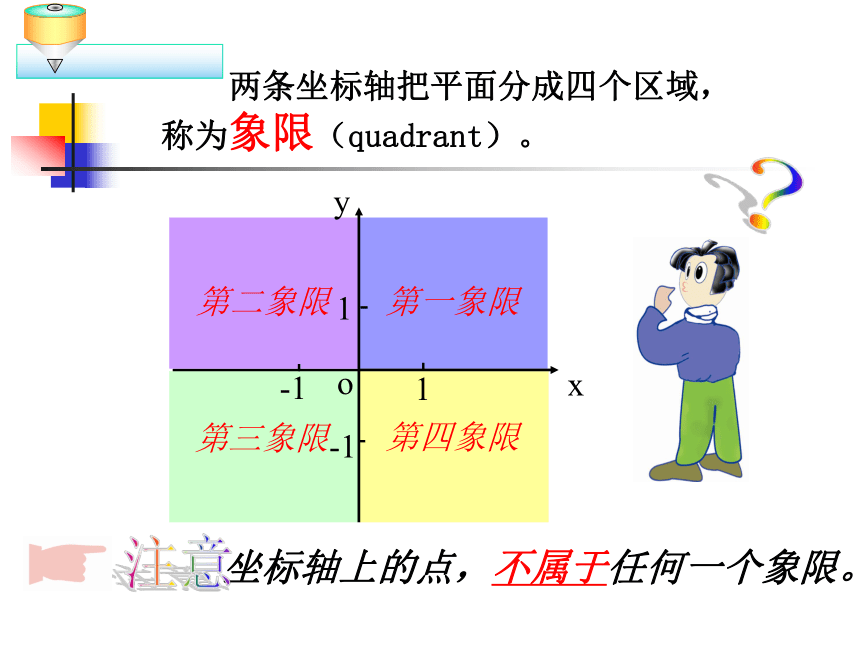
课件22张PPT。6.2平面直角坐标系北（1）“镇海楼”的位置在“人民广场”东多少格，北多少格？用有序数对表示“镇海楼”的位置，“玉泉”的位置在“人民广场”西多少格，南多少格？用有序数对表示“玉泉”的位置。北（2）“灵石塔”的位置在“人民广场”西多少格，北多少格？，怎样用有序数对表示“灵石塔”的位置？6.2 平面直角坐标系(1)概念纵轴平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系，简称为直角坐标系( rectangular coordinates) 。水平方向的数轴称为x轴(x-axis) 或横轴，竖直方向的数轴称为y轴 (y-axis)或纵轴，它们统称为坐标轴。公共原点O称为坐标原点 (origin) P（2，-3）坐标系所在的平面叫做坐标平面。想一想：坐标系有什么特征？在同一平面内两条数轴：①互相垂直；②原点重合；③通常取向右、向上为正方向；④单位长度一般取相同的。第一象限第四象限第二象限第三象限 两条坐标轴把平面分成四个区域，
称为象限（quadrant）。？xyo坐标轴上的点，不属于任何一个象限。注意1-1-11因此，我们可以提出这样一个问题：
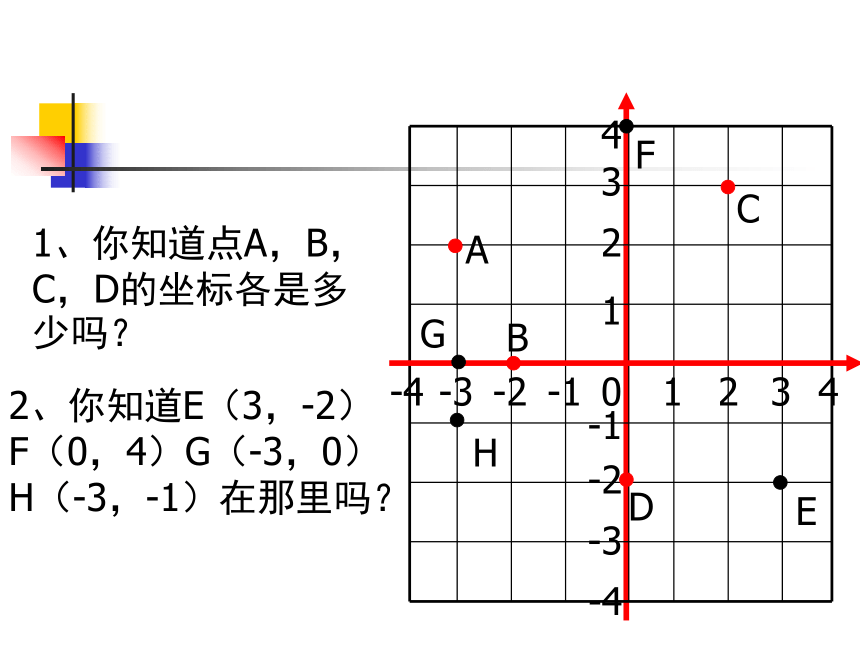
x轴和y轴把坐标平面分成几个部分？它们分别叫什么？答：分成五个部分，分别叫做第一象限、第二象限、第三象限、第四象限和坐标轴。1、你知道点A，B，C，D的坐标各是多少吗？2、你知道E（3，-2）F（0，4）G（-3，0）H（-3，-1）在那里吗？432121-15-2-3-4543-4-2-1O-3xyABDCE例1 如图所示, 写出坐标平面内点A、B、C、D、E、F、O的坐标。（2,4）（-2,2）（0,-2.5）（2, -2.5 ）（-3,0）F（-3.5, -2 .5）(0,0)试一试例2 在平面直角坐标系中，描出下列各点
A(4, 3) , B(-2, 3)，C(-3.5, -2), D(1.5, -1.5)画一画·A··DCxyB·. 坐标平面内，点的坐标各有什么特点? y 轴 （ ， ）第一象限（ ， ）第二象限（ ， ）第三象限（ ， ）第四象限（ ， ）坐标原点（ ， ） x 轴 （ ， ）－ ＋－ －＋ －0 0x 00 y(＋,＋)(＋, －)(－, －)(－, ＋)＋ ＋动动脑筋！动动脑筋！ 坐标平面内，坐标轴上的点有什么特点?1、点在横轴上，纵坐标为0。2、点在纵轴上，横坐标为0。延伸与提高4.说出下列各点所在的象限或坐标轴：A(－3,－5)第三象限B(6, －7)第四象限C(0, －6)y轴D(－3, 5)第二象限E(4, 0)x轴F(3.5, 2)第一象限G(3, -4.2)第四象限O(0, 0)x轴y轴规则是：第一象限内的点由第一大组的同学回答,第二象限内的点由第二大组的同学回答;以此类推.
坐标轴上的点由同学个别举手抢答.原点yxo123-2-1-1-2123-4-3门讲台················································点到名字的同学请说出你的坐标我来找一找 :
5. 如图建立平面直角坐标系，下面请大家找一找自己在坐标系中的坐标分别是什么?门yxo123-2-1-1-2123-4-3门讲台················································条件反射 ① 请坐标是A(1,3) B(2,-1) C(-2,2) D(2,0) E(0,1) F(-4,-1) O（0，0）的同学起立;②请自己的横坐标与纵坐标的数相同的同学起立;③请自己的横坐标与纵坐标互为相反数的同学起立。练习6门横纵坐标相同的点在一、三象限的角平分线上。横纵坐标是互为相反数的点在二、四象限的角平分线上做一做：1、在如图所示的平面直角坐标系中画出点M（-1，0），N（2，2），P（1.5，-1.5），Q（-4，-4）。NMPQ.022-2-244-4-46-6xy做一做：2、（1）写出图中六边形各个顶点的坐标，它们各在什么象限内或坐标轴上？那些点的横坐标相同？那些点的纵坐标相同？（2）作出点（- ，2 ）（- , 2 ）做一做：3、指出图中点A，B，C，D，E，F，G分别在那一个象限，并写出各点的坐标。.......ABCDEFGxyABCDABCD 如图，正方形ABCD的边长为6，如果以A点为原点,AB所在直线为x轴，AD所在的直线为y轴，建立如图所示平面直角坐标系，　写出正方形的顶点A、B、C、D 的坐标。 请另建立一个直角坐标系，这时
正方形的顶点A、B、C、D的坐标又分
别是多少？探究 如图，已知等边三角形OAB的一个顶点为A（2，0）求其余2个顶点的坐标。再见