5.1 矩形-2024-2025学年浙教版八年级下册 同步分层作业(含解析)
文档属性
| 名称 | 5.1 矩形-2024-2025学年浙教版八年级下册 同步分层作业(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 17:23:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.1 矩形 同步分层作业
1.下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等 C.对角线互相垂直 D.是轴对称图形
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
3.周末,小刚去正在装修的房屋查看进度,放在地上的一块地板砖(如图)吸引了他的注意,于是他找来卷尺进行如下操作:①测量地板砖的两组对边长度是否分别相等;②测量地板砖的两条对角线是否相等,以此判断地板砖的表面是否为矩形.小刚的判断依据是( )
A.对角线相等的平行四边形是矩形 B.有三个角是直角的四边形是矩形
C.有一个角是直角的平行四边形是矩形 D.对角线相等的四边形是矩形
4.活动课上,小明用四根细木条搭成如图所示的一个四边形,现要判断这个四边形是否是矩形,以下测量方案正确的是( )
A.测量是否有三个角是直角 B.测量对角线是否相等
C.测量两组对边是否分别相等 D.测量对角线是否互相垂直
5.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
A.36° B.27° C.18° D.9°
6.如图,在 ABCD中,AC,BD交于点O.添加下列一个条件,仍不能判定 ABCD是矩形,该条件是( )
A.∠AOB=90° B.∠ABC=90° C.AC=BD D.∠OAD=∠ODA
7.已知四边形ABCD是平行四边形,下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=90° B.∠B=∠C C.AC=BD D.AC⊥BD
8.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线交AD,BC于E,F两点,若AC=6,∠AEO=120°,则OE的长为( )
A.1 B.2 C. D.
9.如图,在矩形ABCD中,AB=6,AD=8,E是AD上一点,AE=3,P是BC上一动点,连接AP,取AP的中点F,连接EF,则线段EF取得最小值是( )
A.3 B.4 C.5 D.6
10.如图,在矩形ABCD中,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于点M,N作直线MN,交BC于点E,交AD于点F,若BE=3,AF=5,则矩形的周长为( )
A.8 B.20 C.24 D.30
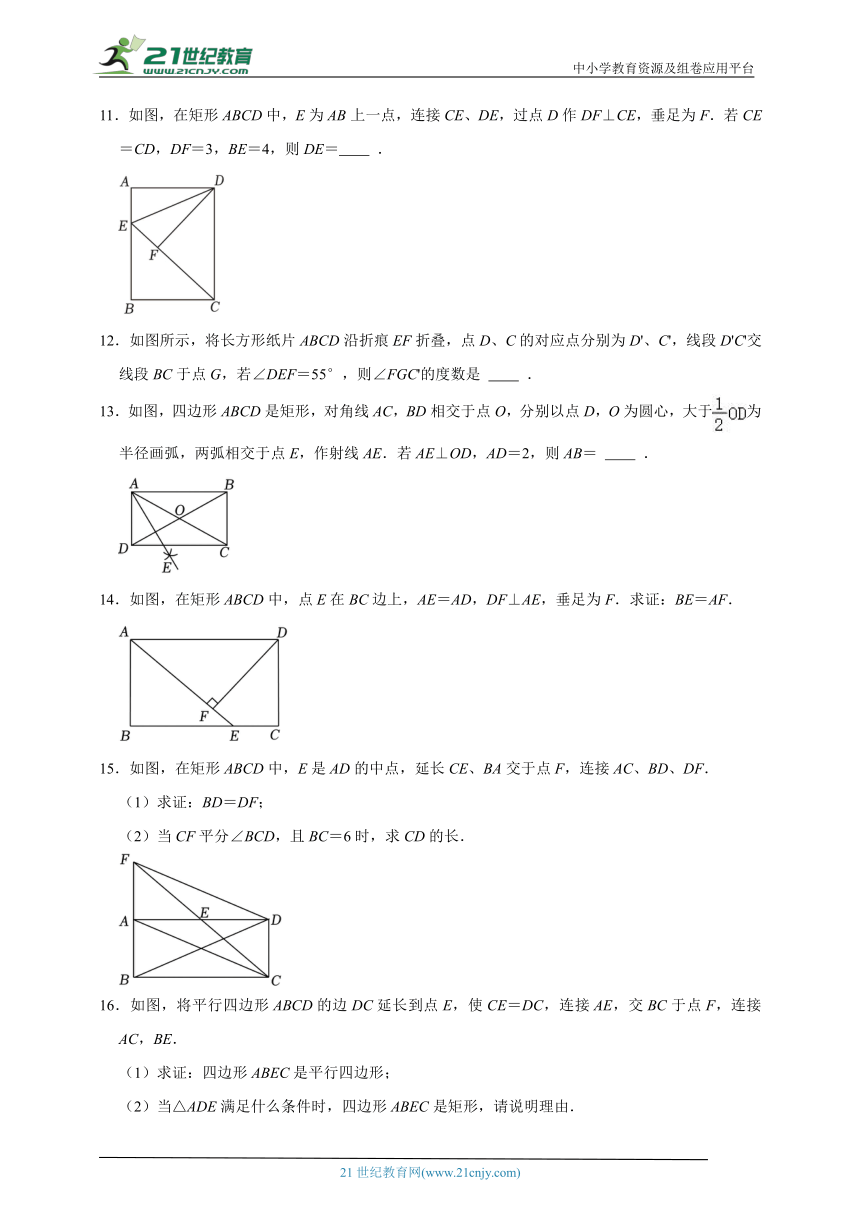
11.如图,在矩形ABCD中,E为AB上一点,连接CE、DE,过点D作DF⊥CE,垂足为F.若CE=CD,DF=3,BE=4,则DE= .
12.如图所示,将长方形纸片ABCD沿折痕EF折叠,点D、C的对应点分别为D'、C',线段D'C'交线段BC于点G,若∠DEF=55°,则∠FGC'的度数是 .
13.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,分别以点D,O为圆心,大于为半径画弧,两弧相交于点E,作射线AE.若AE⊥OD,AD=2,则AB= .
14.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.求证:BE=AF.
15.如图,在矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、BD、DF.
(1)求证:BD=DF;
(2)当CF平分∠BCD,且BC=6时,求CD的长.
16.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC,BE.
(1)求证:四边形ABEC是平行四边形;
(2)当△ADE满足什么条件时,四边形ABEC是矩形,请说明理由.
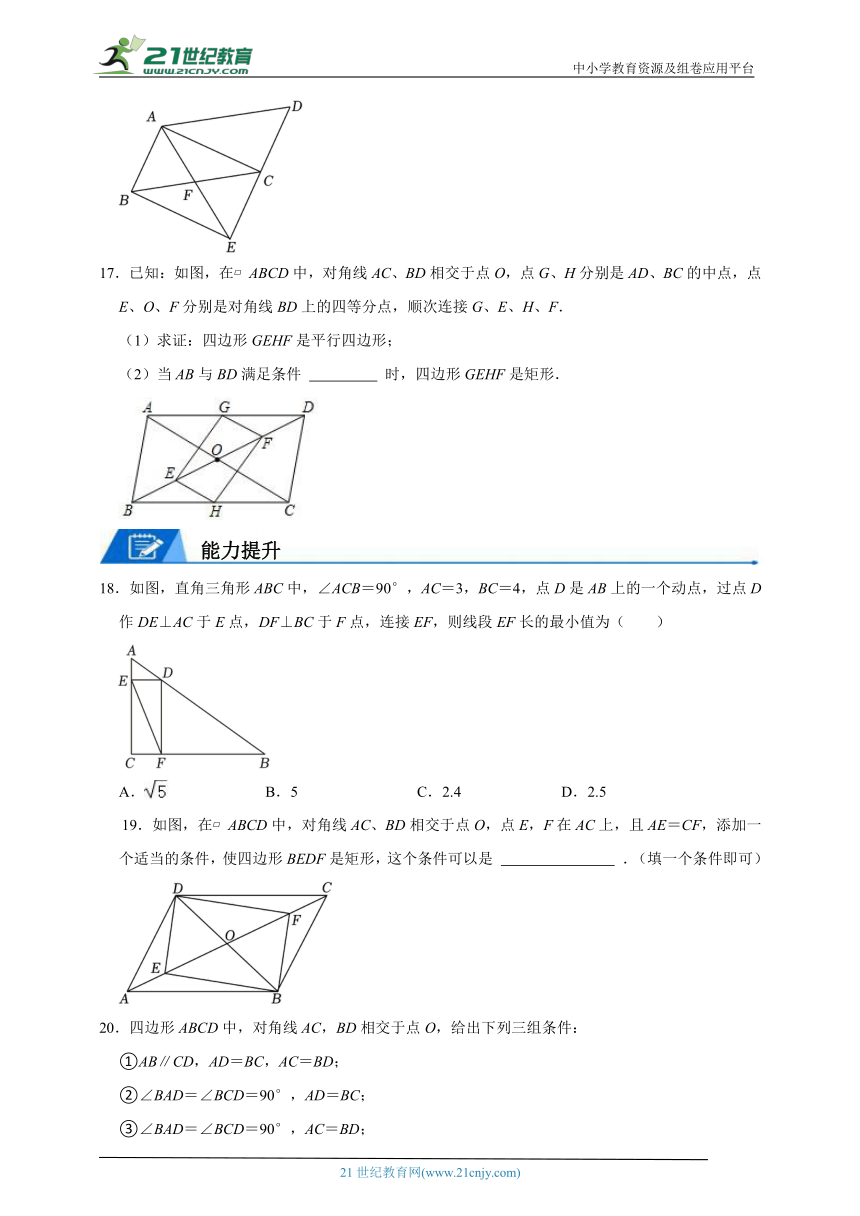
17.已知:如图,在 ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当AB与BD满足条件 时,四边形GEHF是矩形.
18.如图,直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点D是AB上的一个动点,过点D作DE⊥AC于E点,DF⊥BC于F点,连接EF,则线段EF长的最小值为( )
A. B.5 C.2.4 D.2.5
19.如图,在 ABCD中,对角线AC、BD相交于点O,点E,F在AC上,且AE=CF,添加一个适当的条件,使四边形BEDF是矩形,这个条件可以是 .(填一个条件即可)
20.四边形ABCD中,对角线AC,BD相交于点O,给出下列三组条件:
①AB∥CD,AD=BC,AC=BD;
②∠BAD=∠BCD=90°,AD=BC;
③∠BAD=∠BCD=90°,AC=BD;
其中一定能判定这个四边形是矩形的条件有 .(填写所有正确条件的序号)
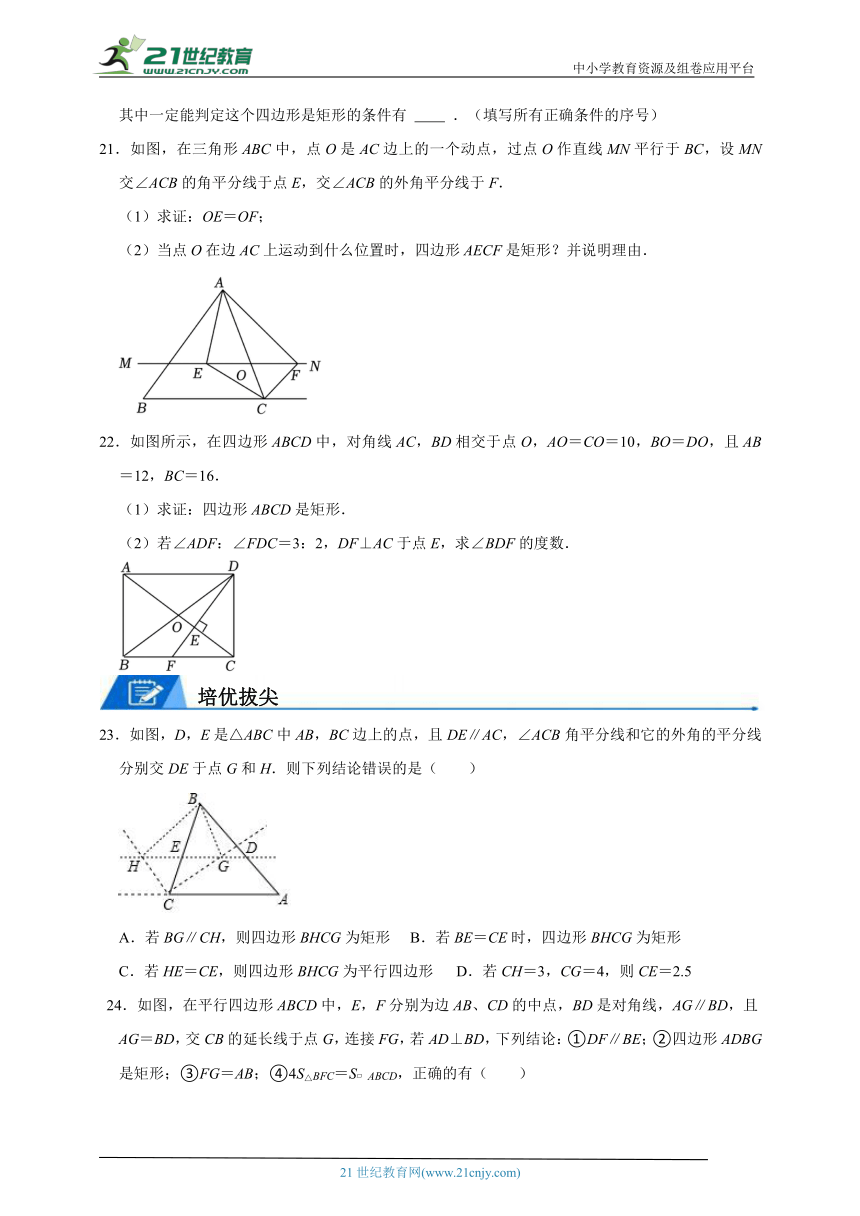
21.如图,在三角形ABC中,点O是AC边上的一个动点,过点O作直线MN平行于BC,设MN交∠ACB的角平分线于点E,交∠ACB的外角平分线于F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
22.如图所示,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,且AB=12,BC=16.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC于点E,求∠BDF的度数.
23.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形 B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形 D.若CH=3,CG=4,则CE=2.5
24.如图,在平行四边形ABCD中,E,F分别为边AB、CD的中点,BD是对角线,AG∥BD,且AG=BD,交CB的延长线于点G,连接FG,若AD⊥BD,下列结论:①DF∥BE;②四边形ADBG是矩形;③FG=AB;④4S△BFC=S ABCD,正确的有( )
A.①②③④ B.①② C.①③ D.①②④
25.如图,在矩形ABCD中,AD=12cm,点P从点A向点D以1cm/s的速度运动,点Q以4cm/s的速度从点C出发.在B,C两点之间做往返运动,两点同时出发,点P到达点D时,两点同时停止运动,这段时间内,若以P,Q,C,D四点为顶点的四边形是矩形,那么运动时间为 .
26.如图, ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)在不添加新的点和线的前提下,增加一个条件: ,使得四边形AOBE是矩形,并说明理由;
(2)若AC⊥BD,OE=10,AC=16,求 ABCD的面积.
27.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,点使CF=BE,连接AF、DE、DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,BF=10,DE=8,求AE的长.
答案与解析
1.下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等 C.对角线互相垂直 D.是轴对称图形
【点拨】根据矩形的性质,即对角线平分相等,及是轴对称图形又是中心对称图形,进行解答即可.
【解析】解:A.矩形对角线互相平分且相等,不符合题意;B.矩形的四个角相等,不符合题意;C.矩形的对角线互相平分且相等,符合题意;
D.矩形既是轴对称图形,又是中心对称图形,不符合题意,故选:C.
【点睛】本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
【点拨】根据矩形的性质得出AC=BD,AO=CO,求出AC,再求出BD即可.
【解析】解:∵四边形ABCD是矩形,
∴AC=BD,AO=CO,
∵AO=3,
∴CO=3,
∴AC=3+3=6,
∴BD=AC=6,
故选:D.
【点睛】本题考查了矩形的性质,能熟记矩形的对角线互相平分且相等是解此题的关键.
3.周末,小刚去正在装修的房屋查看进度,放在地上的一块地板砖(如图)吸引了他的注意,于是他找来卷尺进行如下操作:①测量地板砖的两组对边长度是否分别相等;②测量地板砖的两条对角线是否相等,以此判断地板砖的表面是否为矩形.小刚的判断依据是( )
A.对角线相等的平行四边形是矩形 B.有三个角是直角的四边形是矩形
C.有一个角是直角的平行四边形是矩形 D.对角线相等的四边形是矩形
【点拨】利用①判定平行四边形,再利用②判定矩形,即可得判断依据.
【解析】解:由②测量地板砖的两条对角线是否相等,
即AC=BD,
则利用“对角线相等的平行四边形是矩形”可判断四边形ABCD是矩形;
故选:A.
【点睛】本题考查平行四边形的判定,矩形的判定,熟练掌握平行四边形和矩形的判定是解题的关键.
4.活动课上,小明用四根细木条搭成如图所示的一个四边形,现要判断这个四边形是否是矩形,以下测量方案正确的是( )
A.测量是否有三个角是直角 B.测量对角线是否相等
C.测量两组对边是否分别相等 D.测量对角线是否互相垂直
【点拨】由矩形的判定方法可求解.
【解析】解:∵三个角是直角的四边形是矩形,
∴选项A正确,
故选:A.
【点睛】本题考查了矩形的判定,掌握矩形的判定方法是解题的关键.
5.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
A.36° B.27° C.18° D.9°
【点拨】利用矩形的性质结合∠ADE:∠EDC=3:2,求解∠ADE=90°×=54°,再求解∠BDA=∠OAD=36°,再利用角的和差即可得到答案.
【解析】解:∵矩形ABCD中,
∴∠ADC=90°,OA=OB=OC=OD,
∵∠ADE:∠EDC=3:2,
∴∠ADE=90°×=54°,
∵DE⊥AC于E,
∴∠DAE=90°﹣54°=36°,
∵OA=OD,
∴∠BDA=∠OAD=36°,
∴∠BDE=∠ADE﹣∠ADO=54°﹣36°=18°.
故选:C.
【点睛】本题考查的是矩形的性质,等腰三角形的性质,掌握“矩形的对角线相等且互相平分”是解本题的关键.
6.如图,在 ABCD中,AC,BD交于点O.添加下列一个条件,仍不能判定 ABCD是矩形,该条件是( )
A.∠AOB=90° B.∠ABC=90° C.AC=BD D.∠OAD=∠ODA
【点拨】根据平行四边形的性质,矩形的判定方法即可一一判断即可.
【解析】解:∵四边形ABCD是平行四边形,∠AOB=90°,
∴AC⊥BD,
∴ ABCD是菱形,故A错误;符合题意;
∵四边形ABCD是平行四边形,∠ABC=90°,
∴ ABCD是矩形,故B不符合题意;
∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD是矩形,故C不符合题意;
∵四边形ABCD是平行四边形,
∴AC=2AO,OD=2BD,
∵∠OAD=∠ODA,
∴OA=OD,
∴AC=BD,
∴ ABCD是矩形,故D不符合题意;
故选:A.
【点睛】本题考查了矩形的判定,平行四边形的性质,熟练掌握矩形的判定定理是解题的关键.
7.已知四边形ABCD是平行四边形,下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=90° B.∠B=∠C C.AC=BD D.AC⊥BD
【点拨】根据有一个角等于90°的平行四边形是矩形可对选项A进行判断;根据平行四边形性质得AB∥CD,则∠B+∠C=180°,再根据∠B=∠C得∠B=∠C=90°,然后根据有一个角等于90°的平行四边形是矩形可对选项B进行判断;根据对角线相等的平行四边形是矩形可对选项C进行判断;根据对角线互相垂直的平行四边形是菱形可对选项D进行判断,综上所述即可得出答案.
【解析】解:A、已知四边形ABCD是平行四边形,
∴当∠A=90°,平行四边形ABCD是矩形,
∴可以判定 ABCD为矩形,
故该选项不符合题意;
B、已知四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
当∠B=∠C时,则∠B=∠C=90°,此时 ABCD为矩形,
∴可以判定 ABCD为矩形,
故该选项不符合题意;
C、已知四边形ABCD是平行四边形,
当AC=BD时,平行四边形ABCD是矩形,
∴可以判定 ABCD为矩形,
故该选项不符合题意;
D、已知四边形ABCD是平行四边形,
当AC⊥BD时,平行四边形ABCD是菱形,
∴不能判定 ABCD为矩形,
故该选项符合题意.
故选:D.
【点睛】本题主要考查了平行四边形的性质,矩形的判定,理解平行四边形的性质,熟练掌握矩形的判定是解决问题的关键.
8.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线交AD,BC于E,F两点,若AC=6,∠AEO=120°,则OE的长为( )
A.1 B.2 C. D.
【点拨】由矩形的性质及直角三角形的性质可得出答案.
【解析】解:∵EF⊥BD,∠AEO=120°,
∴∠EDO=30°,∠DEO=60°,
∵四边形ABCD是矩形,
∴AC=BD,
又∵Rt△BOF中,OD=OB==3,
∴,
∴OE=(负值舍),
故选:D.
【点睛】本题考查了矩形的性质、直角三角形的性质,需要熟练掌握并灵活运用.
9.如图,在矩形ABCD中,AB=6,AD=8,E是AD上一点,AE=3,P是BC上一动点,连接AP,取AP的中点F,连接EF,则线段EF取得最小值是( )
A.3 B.4 C.5 D.6
【点拨】过点P作PM∥EF交AD于点M,易知EF是△APM的中位线,可得PM=2EF,当PM取得最小值时,EF最小,根据垂线段最短求出最小值即可.
【解析】解:过点P作PM∥EF交AD于点M,
由条件可知EF是△APM的中位线,
∴AM=2AE=6,PM=2EF,
当PM取得最小值时,EF最小,
当PM⊥AD时,PM最小,此时PM=AB=6,
∴EF最小=PM最小==3.
故选:A.
【点睛】本题考查了矩形的性质、三角形中位线定理、垂线段最短,熟练掌握以上知识点是关键.
10.如图,在矩形ABCD中,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于点M,N作直线MN,交BC于点E,交AD于点F,若BE=3,AF=5,则矩形的周长为( )
A.8 B.20 C.24 D.30
【点拨】根据作图过程可得,MN是AC的垂直平分线,再由矩形的性质可以证明△AFO≌△CEO,可得AF=CE=AE=5,再根据勾股定理可得AB的长,进而可得矩形的周长.
【解析】解:如图,连接AE,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠FAC=∠ECA,
根据作图过程可知:MN是AC的垂直平分线,
∴∠FOA=∠EOC=90°,AO=CO,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
∴AF=CE,
∵AE=CE,
∴AE=CE=AF=5,
∴BC=BE+CE=3+5=8,
在Rt△ABE中,根据勾股定理,得
AB==4,
∴矩形的周长为2(AB+BC)=2(4+8)=24.
故选:C.
【点睛】本题考查了矩形的性质,作图﹣基本作图,线段垂直平分线的性质,解决本题的关键是掌握基本作图方法.
11.如图,在矩形ABCD中,E为AB上一点,连接CE、DE,过点D作DF⊥CE,垂足为F.若CE=CD,DF=3,BE=4,则DE= .
【点拨】根据矩形的性质得出AB∥CD,∠B=90°,进而利用AAS证明△CFD≌△EBC,根据全等三角形的性质求出CF=BE=4,DF=BC=3=AD,再根据勾股定理求解即可.
【解析】证明:在矩形ABCD中,DF⊥CE于点F,
∴AB∥CD,∠A=∠B=∠DCB=90°,∠DFC=90°,AD=BC,AB=CD,
∴∠DFC=∠B,∠DCF=∠CEB,
在△CFD与△EBC中,
,
∴△CFD≌△EBC(AAS),
∴CF=BE=4,DF=BC=3=AD,
∴CD===5=AB,
∴AE=AB﹣BE=5﹣4=1,
∴DE===,
故答案为:.
【点睛】本题考查矩形的性质,全等三角形的判定与性质,解答本题的关键是熟练掌握全等三角形的判定定理.
12.如图所示,将长方形纸片ABCD沿折痕EF折叠,点D、C的对应点分别为D'、C',线段D'C'交线段BC于点G,若∠DEF=55°,则∠FGC'的度数是 20° .
【点拨】根据折叠的性质和矩形的性质、以及平行线的性质,可以求得∠EFC′、∠C′,∠GFC′的度数,然后根据三角形内角和,即可求得∠FGC′的度数.
【解析】解:由题意可得,
∠EFC=∠EFC′,∠C=∠C′=90°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠EFG,∠DEF+∠EFC=180°,
∵∠DEF=55°,
∴∠EFG=55°,∠EFC=125°,
∴∠EFC′=125°,
∴∠GFC′=∠EFC′﹣∠EFG=125°﹣55°=70°,
∴∠FGC′=180°﹣∠C′﹣∠GFC′=180°﹣90°﹣70°=20°,
故答案为:20°.
【点睛】本题考查矩形的性质、平行线的性质、折叠的性质,解答本题的关键是明确题意,找出所求问题需要的条件.
13.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,分别以点D,O为圆心,大于为半径画弧,两弧相交于点E,作射线AE.若AE⊥OD,AD=2,则AB= 2 .
【点拨】由作图过程可得AE是DO的垂直平分线,得AD=AO=OB=OD=2,进而可以解决问题.
【解析】解:∵四边形ABCD是矩形,
∴AO=CO=OB=OD,∠BAD=90°,
由作图过程和AE⊥OD可知:AE是DO的垂直平分线,
∴AD=AO,
∴AD=AO=OB=OD=2,
∴AB=AD=2,
故答案为:2.
【点睛】本题考查了矩形的性质、作图﹣基本作图、垂直平分线的性质,解决本题的关键是掌握基本作图方法.
14.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.求证:BE=AF.
【点拨】由矩形性质及DF⊥AE,导角可得∠ADF=∠BAE.从而可证明△ADF≌△EAB(AAS),进而可证明结论.
【解析】证明:∵四边形ABCD为矩形,
∴∠DAB=90°=∠DAF+∠BAE,∠B=90°.
又∵DF⊥AE,
∴∠DAF+∠ADF=90°,
∴∠ADF=∠BAE.
在△ADF和△EAB中,
,
∴△ADF≌△EAB(AAS),
∴BE=AF.
【点睛】本题考查了矩形的性质,全等三角形的判定与性质,熟练掌握以上知识点是解题关键.
15.如图,在矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、BD、DF.
(1)求证:BD=DF;
(2)当CF平分∠BCD,且BC=6时,求CD的长.
【点拨】(1)证明△FAE≌△CDE得出CD=FA,可证四边形ACDF是平行四边形,可得AC=DF,即可得出结论;
(2)证出△CDE是等腰直角三角形,得出CD=DE,得出AD=BC=2CD,即可求解.
【解析】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AD=BC,AC=BD,
∴∠FAE=∠CDE.
∵E是AD的中点,
∴AE=DE.
在△FAE和△CDE中,
,
∴△FAE≌△CDE(AAS),
∴CD=FA.
∵CD∥AF,
∴四边形ACDF是平行四边形,
∴AC=DF,
∴BD=DF;
(2)解:∵CF平分∠BCD,
∴∠DCE=45°.
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE.
∵E是AD的中点,
∴AD=2DE=2CD,
∴BC=2CD=6,
∴CD=3.
【点睛】本题考查了矩形的性质、平行四边形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握矩形的性质是解题的关键.
16.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC,BE.
(1)求证:四边形ABEC是平行四边形;
(2)当△ADE满足什么条件时,四边形ABEC是矩形,请说明理由.
【点拨】(1)根据平行四边形的性质得出AB=CD,AB∥CD,求出AB∥CE,AB=CE,根据平行四边形的判定得出即可;
(2)根据平行四边形的性质得出AD=BC,求出AE=BC,根据矩形的判定得出即可.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵CE=CD,
∴AB∥CE,AB=CE,
∴四边形ABEC是平行四边形;
(2)解:当AE=AD,四边形ABEC是矩形,
理由:∵四边形ABCD是平行四边形,
∴AD=BC,
∵AE=AD,
∴AE=BC,
由(1)知:四边形ABEC是平行四边形,
∴四边形ABEC是矩形.
【点睛】本题考查了平行四边形的性质和判定,矩形的判定的应用,能灵活运用定理进行推理是解此题的关键,注意:对角线相等的平行四边形是矩形.
17.已知:如图,在 ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当AB与BD满足条件 BD=2AB 时,四边形GEHF是矩形.
【点拨】(1)由三角形中位线定理得GF∥OA,GF=OA,同理EH∥OC,EH=OC,再由平行四边形的性质得OA=OC,则EH∥GF,EH=GF,即可得出结论;
(2)连接GH,由平行四边形的性质得AD∥BC,AD=BC,OB=OD,再证四边形ABHG是平行四边形,得AB=GH,然后证GH=EF,即可得出结论.
【解析】(1)证明:∵G,F分别为AD,DO的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理可得:EH∥OC,EH=OC,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴EH∥GF,EH=GF,
∴四边形GEHF是平行四边形;
(2)解:当BD=2AB时,四边形GEHF是矩形.
理由:如图,连接GH,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∵G,H分别是AD,BC的中点,
∴AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB=GH,
∵E,F分别是BO,DO的中点,
∴BE=OE=OF=DF,
∴BD=2EF,
∵BD=2AB,
∴EF=AB,
∴GH=EF,
∴平行四边形GEHF是矩形.
【点睛】本题考查了矩形的判定、平行四边形的判定与性质、三角形中位线定理等知识,熟练掌握菱形的判定和平行四边形的判定与性质是解题的关键.
18.如图,直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点D是AB上的一个动点,过点D作DE⊥AC于E点,DF⊥BC于F点,连接EF,则线段EF长的最小值为( )
A. B.5 C.2.4 D.2.5
【点拨】作CH⊥AB于点H,连接CD,上∠ACB=90°,AC=3,BC=4,求得AB=5,由S△ABC=×5CH=×3×4,求得CH=2.4,由DE⊥AC于E点,DF⊥BC于F点,证明四边形ECFD是矩形,则CD=EF,由CD≥CH,得EF≥2.4,则线段EF的最小值为2.4,于是得到问题的答案.
【解析】解:作CH⊥AB于点H,连接CD,
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵S△ABC=×5CH=×3×4,
∴CH=2.4,
∵DE⊥AC于E点,DF⊥BC于F点,
∴∠DEC=∠DFC=∠ECF=90°,
∴四边形ECFD是矩形,
∴CD=EF,
∵CD≥CH,
∴EF≥2.4,
∴线段EF的最小值为2.4,
故选:C.
【点睛】此题重点考查勾股定理、矩形的判定与性质、垂线段最短、根据面积等式求线段的长度等知识与方法,正确地添加辅助线是解题的关键.
19.如图,在 ABCD中,对角线AC、BD相交于点O,点E,F在AC上,且AE=CF,添加一个适当的条件,使四边形BEDF是矩形,这个条件可以是 ∠BED=90°(答案不唯一) .(填一个条件即可)
【点拨】由平行四边形的性质得OA=OC,OB=OD,进而证明OE=OF,再证明四边形BEDF是平行四边形,然后由矩形的判定即可得出结论.
【解析】解:这个条件可以是∠BED=90°,理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形BEDF是平行四边形,
又∵∠BED=90°,
∴平行四边形BEDF是矩形,
故答案为:∠BED=90°(答案不唯一).
【点睛】本题考查了菱形的判定以及平行四边形的判定与性质等知识,熟练掌握菱形的判定和平行四边形的判定与性质是解题的关键.
20.四边形ABCD中,对角线AC,BD相交于点O,给出下列三组条件:
①AB∥CD,AD=BC,AC=BD;
②∠BAD=∠BCD=90°,AD=BC;
③∠BAD=∠BCD=90°,AC=BD;
其中一定能判定这个四边形是矩形的条件有 ②③ .(填写所有正确条件的序号)
【点拨】矩形的判定:需满足“三个角是直角”或“平行四边形+一个直角”或“平行四边形+对角线相等”等条件.
①需判断是否为平行四边形或等腰梯形,排除非矩形情况.
②通过构造反例验证是否可能形成非矩形的直角四边形
③利用对角线相等和直角条件,推导其他角是否为直角.
【解析】解:①条件:AB∥CD,AD=BC,AC=BD.推理:AB∥CD且AD=BC,可能为等腰梯形.等腰梯形满足AC=BD,但等腰梯形不一定是矩形.结论:无法确定为矩形.
②条件:∠BAD=∠BCD=90°,AD=BC.推理:∵,∴△ABD≌△CDB(HL),∴∠ADB=∠CBD,∴AD∥BC,∴四边形ABCD为矩形.结论:确定为矩形.
③条件:∠BAD=∠BCD=90°,AC=BD.
推理:设A(0,0),D(0,a),B(b,0),C(c,d),
由∠BCD=90°,得(c﹣b)c+(d﹣a)d=0.
由AC=BD,得,联立方程可得b=0,a=d,即B(0,0),C(a,a),此时四边形为矩形.结论:必为矩形.
故选:②③.
【点睛】本题主要考查矩形的判定条件,解题的关键是结合四边形的性质进行推理.
21.如图,在三角形ABC中,点O是AC边上的一个动点,过点O作直线MN平行于BC,设MN交∠ACB的角平分线于点E,交∠ACB的外角平分线于F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
【点拨】(1)由角平分线的定义得∠ACE=∠BCE,∠ACF=∠GCF,再由平行线的性质得∠OEC=∠BCE,∠OFC=∠GCF,则∠OEC=∠ACE,∠OFC=∠ACF,然后证明EO=CO,FO=CO,即可得出结论;
(2)先证明四边形AECF是平行四边形,再证明AC=EF,然后由矩形的判定即可得出结论.
【解析】(1)证明:如图,
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠ACE=∠BCE,∠ACF=∠GCF,
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
∴∠OEC=∠ACE,∠OFC=∠ACF,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形,理由如下:
当O为AC的中点时,AO=CO,
由(1)可知,EO=FO=CO,
∴四边形AECF是平行四边形,
∵OA+OC=OE+OF,
即AC=EF,
∴平行四边形AECF是矩形.
【点睛】本题考查了矩形的判定、平行四边形的判定与性质、平行线的性质、等腰三角形的判定等知识,熟练掌握矩形的判定和等腰三角形的判定是解题的关键.
22.如图所示,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,且AB=12,BC=16.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC于点E,求∠BDF的度数.
【点拨】(1)先证明四边形ABCD是平行四边形,利用勾股定理逆定理,得到∠ABC=90°,即可得证;
(2)求出∠FDC的度数,根据三角形的内角和,求出∠DCO,然后根据OD=OC,得到∠CDO,即可求出∠BDF的度数.
【解析】(1)证明:∵在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,
∴四边形ABCD是平行四边形,AC=AO+CO=20,
∵AB=12,BC=16,
∴AB2+BC=122+162=202=AC2,
∴∠ABC=90°,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形
∴∠ADC=90°,
∵∠ADF:∠FDC=3:2,∠ADF+∠FDC=∠ADC,
∴,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
【点睛】本题考查了平行四边形的判定和性质,矩形的判定和性质,能灵活运用定理进行推理是解题的关键.注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.
23.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形 B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形 D.若CH=3,CG=4,则CE=2.5
【点拨】由∠ACB角平分线和它的外角的平分线分别交DE于点G和H可得∠HCG=90°,∠ECG=∠ACG即可得HE=EC=EG,再根据A,B,C,D的条件,进行判断.
【解析】解:∵∠ACB角平分线和它的外角的平分线分别交DE于点G和H,
∴∠HCG=90°,∠ECG=∠ACG;
∵DE∥AC.
∴∠ACG=∠HGC=∠ECG.
∴EC=EG;
同理:HE=EC,
∴HE=EC=EG=HG;
若CH∥BG,
∴∠HCG=∠BGC=90°,
∴∠EGB=∠EBG,
∴BE=EG,
∴BE=EG=HE=EC,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形;
故A正确;
若BE=CE,
∴BE=CE=HE=EG,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形,
故B正确;
若HE=EC,则不可以证明则四边形BHCG为平行四边形,
故C错误;
若CH=3,CG=4,根据勾股定理可得HG=5,
∴CE=2.5,
故D正确.
故选:C.
【点睛】本题考查了矩形的判定,平行四边形的性质和判定,关键是灵活这些判定解决问题.
24.如图,在平行四边形ABCD中,E,F分别为边AB、CD的中点,BD是对角线,AG∥BD,且AG=BD,交CB的延长线于点G,连接FG,若AD⊥BD,下列结论:①DF∥BE;②四边形ADBG是矩形;③FG=AB;④4S△BFC=S ABCD,正确的有( )
A.①②③④ B.①② C.①③ D.①②④
【点拨】①证明四边形DEBF是平行四边形即可;②根据AG∥BD且AG=DB可证四边形ADBG是平行四边形,结合AD⊥BD可证四边形ADBG是矩形;③连接DG,若FG=AB,可证FG=CD,显然不一定成立;④先证明S△BFC=S△BFD,然后结合平行四边形的性质即可求解.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E、F分别为边AB、CD的中点,
∴BE=DF,
∴四边形DEBF是平行四边形,
∴DF∥BE,故①正确;
∵AG∥DB且AG=DB,
∴四边形ADBG是平行四边形,
∵AD⊥BD,
∴四边形ADBG是矩形,故②正确;
连接DG,
∵四边形ADBG是矩形,
∴DG过点E,AB=GD.
若FG=AB,则FG=GD,显然FG与GD不相等,故③不正确;
∵四边形ABCD是平行四边形,
又∵F为边CD的中点,
∴S△BFC=S△BFD,
∴,
∴4S△BFC=S ABCD,故④正确.
综上可知,正确的有①②④,
故选:D.
【点睛】本题考查了平行四边形的判定与性质,矩形的判定与性质,以及三角形的面积公式,熟练掌握平行四边形和矩形的性质是解答本题的关键.
25.如图,在矩形ABCD中,AD=12cm,点P从点A向点D以1cm/s的速度运动,点Q以4cm/s的速度从点C出发.在B,C两点之间做往返运动,两点同时出发,点P到达点D时,两点同时停止运动,这段时间内,若以P,Q,C,D四点为顶点的四边形是矩形,那么运动时间为 或4或或12 .
【点拨】根据运动表示出DP、CQ,结合矩形的判定得到当DP=CQ时以P,Q,C,D四点为顶点的四边形是矩形列式求解即可得到答案.
【解析】解:∵四边形是ABCD矩形,
∴∠D=∠C=90°,AD=BC,
∵AD=12cm,点P从点A向点D以1cm/s的速度运动,点Q以4cm/s的速度从点C出发,在B,C两点之间做往返运动,
∴DP=12﹣t,CQ=4t或CQ=24﹣4t或4t﹣24,
∵以P,Q,C,D四点为顶点的四边形是矩形,
∴DP=CQ,
∴12﹣t=4t或12﹣t=24﹣4t或12﹣t=4t﹣24,
解得:或4或,
故答案为:或4或或12.
【点睛】本题考查了矩形的判定,掌握矩形的判定是解题的关键.
26.如图, ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)在不添加新的点和线的前提下,增加一个条件: AC⊥BD(答案不唯一). ,使得四边形AOBE是矩形,并说明理由;
(2)若AC⊥BD,OE=10,AC=16,求 ABCD的面积.
【点拨】(1)添加:AC⊥BD(答案不唯一).根据有一个角是直角的平行四边形是矩形证明即可;
(2)利用矩形的性质求出AB,再利用勾股定理求出OB,可得结论.
【解析】解:(1)添加:AC⊥BD(答案不唯一).
理由:∵BE∥AC,AE∥BD,
∴四边形AOBE是平行四边形,
∵AC⊥DB,
∴∠AOB=90°,
∴四边形AOBE是矩形;
故答案为:
(2)由(1)可知,四边形AOBE是矩形,
∴AB=OE=10,
∵四边形ABCD是平行四边形,
∴OA=OC=AC=8,
∵AC⊥BD,
∴OD=OB===6,
∴BD=12,
∴四边形ABCD的面积= AC BD=×16×12=96.
【点睛】本题考查平行四边形的性质,矩形的判定和性质,勾股定理,等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
27.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,点使CF=BE,连接AF、DE、DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,BF=10,DE=8,求AE的长.
【点拨】(1)根据平行四边形性质得AD∥BC,AD=BC,再根据CF=BE得EF=BC=AD,由此可判定四边形AEFD为平行四边形,然后再根据AE⊥BC可得出结论;
(2)根据矩形性质得AF=DE=8,再根据勾股定理的逆定理证明∠BAF=90°,然后根据三角形的面积公式即可求出AE的长.
【解析】(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵CF=BE,
∴CF+CE=BE+CE,
即EF=BC,
∴AD=EF,
又∵AD∥BC,
即AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)∵四边形AEFD是矩形,
∴AF=DE=8,
在△ABF中,AB=6,AF=8,BF=10,
∵AB2+AF2=100,BF2=100,
∴AB2+AF2=BF2,
∴△ABF为直角三角形,
即∠BAF=90°,
由三角形的面积公式得:S△ABF=BF AE=AB AF,
∴AE===4.8.
【点睛】此题主要考查了矩形的判定与性质,平行四边形的性质,熟练掌握矩形的判定与性质,平行四边形的性质是解决问题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.1 矩形 同步分层作业
1.下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等 C.对角线互相垂直 D.是轴对称图形
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
3.周末,小刚去正在装修的房屋查看进度,放在地上的一块地板砖(如图)吸引了他的注意,于是他找来卷尺进行如下操作:①测量地板砖的两组对边长度是否分别相等;②测量地板砖的两条对角线是否相等,以此判断地板砖的表面是否为矩形.小刚的判断依据是( )
A.对角线相等的平行四边形是矩形 B.有三个角是直角的四边形是矩形
C.有一个角是直角的平行四边形是矩形 D.对角线相等的四边形是矩形
4.活动课上,小明用四根细木条搭成如图所示的一个四边形,现要判断这个四边形是否是矩形,以下测量方案正确的是( )
A.测量是否有三个角是直角 B.测量对角线是否相等
C.测量两组对边是否分别相等 D.测量对角线是否互相垂直
5.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
A.36° B.27° C.18° D.9°
6.如图,在 ABCD中,AC,BD交于点O.添加下列一个条件,仍不能判定 ABCD是矩形,该条件是( )
A.∠AOB=90° B.∠ABC=90° C.AC=BD D.∠OAD=∠ODA
7.已知四边形ABCD是平行四边形,下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=90° B.∠B=∠C C.AC=BD D.AC⊥BD
8.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线交AD,BC于E,F两点,若AC=6,∠AEO=120°,则OE的长为( )
A.1 B.2 C. D.
9.如图,在矩形ABCD中,AB=6,AD=8,E是AD上一点,AE=3,P是BC上一动点,连接AP,取AP的中点F,连接EF,则线段EF取得最小值是( )
A.3 B.4 C.5 D.6
10.如图,在矩形ABCD中,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于点M,N作直线MN,交BC于点E,交AD于点F,若BE=3,AF=5,则矩形的周长为( )
A.8 B.20 C.24 D.30
11.如图,在矩形ABCD中,E为AB上一点,连接CE、DE,过点D作DF⊥CE,垂足为F.若CE=CD,DF=3,BE=4,则DE= .
12.如图所示,将长方形纸片ABCD沿折痕EF折叠,点D、C的对应点分别为D'、C',线段D'C'交线段BC于点G,若∠DEF=55°,则∠FGC'的度数是 .
13.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,分别以点D,O为圆心,大于为半径画弧,两弧相交于点E,作射线AE.若AE⊥OD,AD=2,则AB= .
14.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.求证:BE=AF.
15.如图,在矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、BD、DF.
(1)求证:BD=DF;
(2)当CF平分∠BCD,且BC=6时,求CD的长.
16.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC,BE.
(1)求证:四边形ABEC是平行四边形;
(2)当△ADE满足什么条件时,四边形ABEC是矩形,请说明理由.
17.已知:如图,在 ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当AB与BD满足条件 时,四边形GEHF是矩形.
18.如图,直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点D是AB上的一个动点,过点D作DE⊥AC于E点,DF⊥BC于F点,连接EF,则线段EF长的最小值为( )
A. B.5 C.2.4 D.2.5
19.如图,在 ABCD中,对角线AC、BD相交于点O,点E,F在AC上,且AE=CF,添加一个适当的条件,使四边形BEDF是矩形,这个条件可以是 .(填一个条件即可)
20.四边形ABCD中,对角线AC,BD相交于点O,给出下列三组条件:
①AB∥CD,AD=BC,AC=BD;
②∠BAD=∠BCD=90°,AD=BC;
③∠BAD=∠BCD=90°,AC=BD;
其中一定能判定这个四边形是矩形的条件有 .(填写所有正确条件的序号)
21.如图,在三角形ABC中,点O是AC边上的一个动点,过点O作直线MN平行于BC,设MN交∠ACB的角平分线于点E,交∠ACB的外角平分线于F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
22.如图所示,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,且AB=12,BC=16.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC于点E,求∠BDF的度数.
23.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形 B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形 D.若CH=3,CG=4,则CE=2.5
24.如图,在平行四边形ABCD中,E,F分别为边AB、CD的中点,BD是对角线,AG∥BD,且AG=BD,交CB的延长线于点G,连接FG,若AD⊥BD,下列结论:①DF∥BE;②四边形ADBG是矩形;③FG=AB;④4S△BFC=S ABCD,正确的有( )
A.①②③④ B.①② C.①③ D.①②④
25.如图,在矩形ABCD中,AD=12cm,点P从点A向点D以1cm/s的速度运动,点Q以4cm/s的速度从点C出发.在B,C两点之间做往返运动,两点同时出发,点P到达点D时,两点同时停止运动,这段时间内,若以P,Q,C,D四点为顶点的四边形是矩形,那么运动时间为 .
26.如图, ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)在不添加新的点和线的前提下,增加一个条件: ,使得四边形AOBE是矩形,并说明理由;
(2)若AC⊥BD,OE=10,AC=16,求 ABCD的面积.
27.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,点使CF=BE,连接AF、DE、DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,BF=10,DE=8,求AE的长.
答案与解析
1.下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等 C.对角线互相垂直 D.是轴对称图形
【点拨】根据矩形的性质,即对角线平分相等,及是轴对称图形又是中心对称图形,进行解答即可.
【解析】解:A.矩形对角线互相平分且相等,不符合题意;B.矩形的四个角相等,不符合题意;C.矩形的对角线互相平分且相等,符合题意;
D.矩形既是轴对称图形,又是中心对称图形,不符合题意,故选:C.
【点睛】本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
【点拨】根据矩形的性质得出AC=BD,AO=CO,求出AC,再求出BD即可.
【解析】解:∵四边形ABCD是矩形,
∴AC=BD,AO=CO,
∵AO=3,
∴CO=3,
∴AC=3+3=6,
∴BD=AC=6,
故选:D.
【点睛】本题考查了矩形的性质,能熟记矩形的对角线互相平分且相等是解此题的关键.
3.周末,小刚去正在装修的房屋查看进度,放在地上的一块地板砖(如图)吸引了他的注意,于是他找来卷尺进行如下操作:①测量地板砖的两组对边长度是否分别相等;②测量地板砖的两条对角线是否相等,以此判断地板砖的表面是否为矩形.小刚的判断依据是( )
A.对角线相等的平行四边形是矩形 B.有三个角是直角的四边形是矩形
C.有一个角是直角的平行四边形是矩形 D.对角线相等的四边形是矩形
【点拨】利用①判定平行四边形,再利用②判定矩形,即可得判断依据.
【解析】解:由②测量地板砖的两条对角线是否相等,
即AC=BD,
则利用“对角线相等的平行四边形是矩形”可判断四边形ABCD是矩形;
故选:A.
【点睛】本题考查平行四边形的判定,矩形的判定,熟练掌握平行四边形和矩形的判定是解题的关键.
4.活动课上,小明用四根细木条搭成如图所示的一个四边形,现要判断这个四边形是否是矩形,以下测量方案正确的是( )
A.测量是否有三个角是直角 B.测量对角线是否相等
C.测量两组对边是否分别相等 D.测量对角线是否互相垂直
【点拨】由矩形的判定方法可求解.
【解析】解:∵三个角是直角的四边形是矩形,
∴选项A正确,
故选:A.
【点睛】本题考查了矩形的判定,掌握矩形的判定方法是解题的关键.
5.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
A.36° B.27° C.18° D.9°
【点拨】利用矩形的性质结合∠ADE:∠EDC=3:2,求解∠ADE=90°×=54°,再求解∠BDA=∠OAD=36°,再利用角的和差即可得到答案.
【解析】解:∵矩形ABCD中,
∴∠ADC=90°,OA=OB=OC=OD,
∵∠ADE:∠EDC=3:2,
∴∠ADE=90°×=54°,
∵DE⊥AC于E,
∴∠DAE=90°﹣54°=36°,
∵OA=OD,
∴∠BDA=∠OAD=36°,
∴∠BDE=∠ADE﹣∠ADO=54°﹣36°=18°.
故选:C.
【点睛】本题考查的是矩形的性质,等腰三角形的性质,掌握“矩形的对角线相等且互相平分”是解本题的关键.
6.如图,在 ABCD中,AC,BD交于点O.添加下列一个条件,仍不能判定 ABCD是矩形,该条件是( )
A.∠AOB=90° B.∠ABC=90° C.AC=BD D.∠OAD=∠ODA
【点拨】根据平行四边形的性质,矩形的判定方法即可一一判断即可.
【解析】解:∵四边形ABCD是平行四边形,∠AOB=90°,
∴AC⊥BD,
∴ ABCD是菱形,故A错误;符合题意;
∵四边形ABCD是平行四边形,∠ABC=90°,
∴ ABCD是矩形,故B不符合题意;
∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD是矩形,故C不符合题意;
∵四边形ABCD是平行四边形,
∴AC=2AO,OD=2BD,
∵∠OAD=∠ODA,
∴OA=OD,
∴AC=BD,
∴ ABCD是矩形,故D不符合题意;
故选:A.
【点睛】本题考查了矩形的判定,平行四边形的性质,熟练掌握矩形的判定定理是解题的关键.
7.已知四边形ABCD是平行四边形,下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=90° B.∠B=∠C C.AC=BD D.AC⊥BD
【点拨】根据有一个角等于90°的平行四边形是矩形可对选项A进行判断;根据平行四边形性质得AB∥CD,则∠B+∠C=180°,再根据∠B=∠C得∠B=∠C=90°,然后根据有一个角等于90°的平行四边形是矩形可对选项B进行判断;根据对角线相等的平行四边形是矩形可对选项C进行判断;根据对角线互相垂直的平行四边形是菱形可对选项D进行判断,综上所述即可得出答案.
【解析】解:A、已知四边形ABCD是平行四边形,
∴当∠A=90°,平行四边形ABCD是矩形,
∴可以判定 ABCD为矩形,
故该选项不符合题意;
B、已知四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
当∠B=∠C时,则∠B=∠C=90°,此时 ABCD为矩形,
∴可以判定 ABCD为矩形,
故该选项不符合题意;
C、已知四边形ABCD是平行四边形,
当AC=BD时,平行四边形ABCD是矩形,
∴可以判定 ABCD为矩形,
故该选项不符合题意;
D、已知四边形ABCD是平行四边形,
当AC⊥BD时,平行四边形ABCD是菱形,
∴不能判定 ABCD为矩形,
故该选项符合题意.
故选:D.
【点睛】本题主要考查了平行四边形的性质,矩形的判定,理解平行四边形的性质,熟练掌握矩形的判定是解决问题的关键.
8.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线交AD,BC于E,F两点,若AC=6,∠AEO=120°,则OE的长为( )
A.1 B.2 C. D.
【点拨】由矩形的性质及直角三角形的性质可得出答案.
【解析】解:∵EF⊥BD,∠AEO=120°,
∴∠EDO=30°,∠DEO=60°,
∵四边形ABCD是矩形,
∴AC=BD,
又∵Rt△BOF中,OD=OB==3,
∴,
∴OE=(负值舍),
故选:D.
【点睛】本题考查了矩形的性质、直角三角形的性质,需要熟练掌握并灵活运用.
9.如图,在矩形ABCD中,AB=6,AD=8,E是AD上一点,AE=3,P是BC上一动点,连接AP,取AP的中点F,连接EF,则线段EF取得最小值是( )
A.3 B.4 C.5 D.6
【点拨】过点P作PM∥EF交AD于点M,易知EF是△APM的中位线,可得PM=2EF,当PM取得最小值时,EF最小,根据垂线段最短求出最小值即可.
【解析】解:过点P作PM∥EF交AD于点M,
由条件可知EF是△APM的中位线,
∴AM=2AE=6,PM=2EF,
当PM取得最小值时,EF最小,
当PM⊥AD时,PM最小,此时PM=AB=6,
∴EF最小=PM最小==3.
故选:A.
【点睛】本题考查了矩形的性质、三角形中位线定理、垂线段最短,熟练掌握以上知识点是关键.
10.如图,在矩形ABCD中,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于点M,N作直线MN,交BC于点E,交AD于点F,若BE=3,AF=5,则矩形的周长为( )
A.8 B.20 C.24 D.30
【点拨】根据作图过程可得,MN是AC的垂直平分线,再由矩形的性质可以证明△AFO≌△CEO,可得AF=CE=AE=5,再根据勾股定理可得AB的长,进而可得矩形的周长.
【解析】解:如图,连接AE,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠FAC=∠ECA,
根据作图过程可知:MN是AC的垂直平分线,
∴∠FOA=∠EOC=90°,AO=CO,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
∴AF=CE,
∵AE=CE,
∴AE=CE=AF=5,
∴BC=BE+CE=3+5=8,
在Rt△ABE中,根据勾股定理,得
AB==4,
∴矩形的周长为2(AB+BC)=2(4+8)=24.
故选:C.
【点睛】本题考查了矩形的性质,作图﹣基本作图,线段垂直平分线的性质,解决本题的关键是掌握基本作图方法.
11.如图,在矩形ABCD中,E为AB上一点,连接CE、DE,过点D作DF⊥CE,垂足为F.若CE=CD,DF=3,BE=4,则DE= .
【点拨】根据矩形的性质得出AB∥CD,∠B=90°,进而利用AAS证明△CFD≌△EBC,根据全等三角形的性质求出CF=BE=4,DF=BC=3=AD,再根据勾股定理求解即可.
【解析】证明:在矩形ABCD中,DF⊥CE于点F,
∴AB∥CD,∠A=∠B=∠DCB=90°,∠DFC=90°,AD=BC,AB=CD,
∴∠DFC=∠B,∠DCF=∠CEB,
在△CFD与△EBC中,
,
∴△CFD≌△EBC(AAS),
∴CF=BE=4,DF=BC=3=AD,
∴CD===5=AB,
∴AE=AB﹣BE=5﹣4=1,
∴DE===,
故答案为:.
【点睛】本题考查矩形的性质,全等三角形的判定与性质,解答本题的关键是熟练掌握全等三角形的判定定理.
12.如图所示,将长方形纸片ABCD沿折痕EF折叠,点D、C的对应点分别为D'、C',线段D'C'交线段BC于点G,若∠DEF=55°,则∠FGC'的度数是 20° .
【点拨】根据折叠的性质和矩形的性质、以及平行线的性质,可以求得∠EFC′、∠C′,∠GFC′的度数,然后根据三角形内角和,即可求得∠FGC′的度数.
【解析】解:由题意可得,
∠EFC=∠EFC′,∠C=∠C′=90°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠EFG,∠DEF+∠EFC=180°,
∵∠DEF=55°,
∴∠EFG=55°,∠EFC=125°,
∴∠EFC′=125°,
∴∠GFC′=∠EFC′﹣∠EFG=125°﹣55°=70°,
∴∠FGC′=180°﹣∠C′﹣∠GFC′=180°﹣90°﹣70°=20°,
故答案为:20°.
【点睛】本题考查矩形的性质、平行线的性质、折叠的性质,解答本题的关键是明确题意,找出所求问题需要的条件.
13.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,分别以点D,O为圆心,大于为半径画弧,两弧相交于点E,作射线AE.若AE⊥OD,AD=2,则AB= 2 .
【点拨】由作图过程可得AE是DO的垂直平分线,得AD=AO=OB=OD=2,进而可以解决问题.
【解析】解:∵四边形ABCD是矩形,
∴AO=CO=OB=OD,∠BAD=90°,
由作图过程和AE⊥OD可知:AE是DO的垂直平分线,
∴AD=AO,
∴AD=AO=OB=OD=2,
∴AB=AD=2,
故答案为:2.
【点睛】本题考查了矩形的性质、作图﹣基本作图、垂直平分线的性质,解决本题的关键是掌握基本作图方法.
14.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.求证:BE=AF.
【点拨】由矩形性质及DF⊥AE,导角可得∠ADF=∠BAE.从而可证明△ADF≌△EAB(AAS),进而可证明结论.
【解析】证明:∵四边形ABCD为矩形,
∴∠DAB=90°=∠DAF+∠BAE,∠B=90°.
又∵DF⊥AE,
∴∠DAF+∠ADF=90°,
∴∠ADF=∠BAE.
在△ADF和△EAB中,
,
∴△ADF≌△EAB(AAS),
∴BE=AF.
【点睛】本题考查了矩形的性质,全等三角形的判定与性质,熟练掌握以上知识点是解题关键.
15.如图,在矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、BD、DF.
(1)求证:BD=DF;
(2)当CF平分∠BCD,且BC=6时,求CD的长.
【点拨】(1)证明△FAE≌△CDE得出CD=FA,可证四边形ACDF是平行四边形,可得AC=DF,即可得出结论;
(2)证出△CDE是等腰直角三角形,得出CD=DE,得出AD=BC=2CD,即可求解.
【解析】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AD=BC,AC=BD,
∴∠FAE=∠CDE.
∵E是AD的中点,
∴AE=DE.
在△FAE和△CDE中,
,
∴△FAE≌△CDE(AAS),
∴CD=FA.
∵CD∥AF,
∴四边形ACDF是平行四边形,
∴AC=DF,
∴BD=DF;
(2)解:∵CF平分∠BCD,
∴∠DCE=45°.
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE.
∵E是AD的中点,
∴AD=2DE=2CD,
∴BC=2CD=6,
∴CD=3.
【点睛】本题考查了矩形的性质、平行四边形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握矩形的性质是解题的关键.
16.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC,BE.
(1)求证:四边形ABEC是平行四边形;
(2)当△ADE满足什么条件时,四边形ABEC是矩形,请说明理由.
【点拨】(1)根据平行四边形的性质得出AB=CD,AB∥CD,求出AB∥CE,AB=CE,根据平行四边形的判定得出即可;
(2)根据平行四边形的性质得出AD=BC,求出AE=BC,根据矩形的判定得出即可.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵CE=CD,
∴AB∥CE,AB=CE,
∴四边形ABEC是平行四边形;
(2)解:当AE=AD,四边形ABEC是矩形,
理由:∵四边形ABCD是平行四边形,
∴AD=BC,
∵AE=AD,
∴AE=BC,
由(1)知:四边形ABEC是平行四边形,
∴四边形ABEC是矩形.
【点睛】本题考查了平行四边形的性质和判定,矩形的判定的应用,能灵活运用定理进行推理是解此题的关键,注意:对角线相等的平行四边形是矩形.
17.已知:如图,在 ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当AB与BD满足条件 BD=2AB 时,四边形GEHF是矩形.
【点拨】(1)由三角形中位线定理得GF∥OA,GF=OA,同理EH∥OC,EH=OC,再由平行四边形的性质得OA=OC,则EH∥GF,EH=GF,即可得出结论;
(2)连接GH,由平行四边形的性质得AD∥BC,AD=BC,OB=OD,再证四边形ABHG是平行四边形,得AB=GH,然后证GH=EF,即可得出结论.
【解析】(1)证明:∵G,F分别为AD,DO的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理可得:EH∥OC,EH=OC,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴EH∥GF,EH=GF,
∴四边形GEHF是平行四边形;
(2)解:当BD=2AB时,四边形GEHF是矩形.
理由:如图,连接GH,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∵G,H分别是AD,BC的中点,
∴AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB=GH,
∵E,F分别是BO,DO的中点,
∴BE=OE=OF=DF,
∴BD=2EF,
∵BD=2AB,
∴EF=AB,
∴GH=EF,
∴平行四边形GEHF是矩形.
【点睛】本题考查了矩形的判定、平行四边形的判定与性质、三角形中位线定理等知识,熟练掌握菱形的判定和平行四边形的判定与性质是解题的关键.
18.如图,直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点D是AB上的一个动点,过点D作DE⊥AC于E点,DF⊥BC于F点,连接EF,则线段EF长的最小值为( )
A. B.5 C.2.4 D.2.5
【点拨】作CH⊥AB于点H,连接CD,上∠ACB=90°,AC=3,BC=4,求得AB=5,由S△ABC=×5CH=×3×4,求得CH=2.4,由DE⊥AC于E点,DF⊥BC于F点,证明四边形ECFD是矩形,则CD=EF,由CD≥CH,得EF≥2.4,则线段EF的最小值为2.4,于是得到问题的答案.
【解析】解:作CH⊥AB于点H,连接CD,
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵S△ABC=×5CH=×3×4,
∴CH=2.4,
∵DE⊥AC于E点,DF⊥BC于F点,
∴∠DEC=∠DFC=∠ECF=90°,
∴四边形ECFD是矩形,
∴CD=EF,
∵CD≥CH,
∴EF≥2.4,
∴线段EF的最小值为2.4,
故选:C.
【点睛】此题重点考查勾股定理、矩形的判定与性质、垂线段最短、根据面积等式求线段的长度等知识与方法,正确地添加辅助线是解题的关键.
19.如图,在 ABCD中,对角线AC、BD相交于点O,点E,F在AC上,且AE=CF,添加一个适当的条件,使四边形BEDF是矩形,这个条件可以是 ∠BED=90°(答案不唯一) .(填一个条件即可)
【点拨】由平行四边形的性质得OA=OC,OB=OD,进而证明OE=OF,再证明四边形BEDF是平行四边形,然后由矩形的判定即可得出结论.
【解析】解:这个条件可以是∠BED=90°,理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形BEDF是平行四边形,
又∵∠BED=90°,
∴平行四边形BEDF是矩形,
故答案为:∠BED=90°(答案不唯一).
【点睛】本题考查了菱形的判定以及平行四边形的判定与性质等知识,熟练掌握菱形的判定和平行四边形的判定与性质是解题的关键.
20.四边形ABCD中,对角线AC,BD相交于点O,给出下列三组条件:
①AB∥CD,AD=BC,AC=BD;
②∠BAD=∠BCD=90°,AD=BC;
③∠BAD=∠BCD=90°,AC=BD;
其中一定能判定这个四边形是矩形的条件有 ②③ .(填写所有正确条件的序号)
【点拨】矩形的判定:需满足“三个角是直角”或“平行四边形+一个直角”或“平行四边形+对角线相等”等条件.
①需判断是否为平行四边形或等腰梯形,排除非矩形情况.
②通过构造反例验证是否可能形成非矩形的直角四边形
③利用对角线相等和直角条件,推导其他角是否为直角.
【解析】解:①条件:AB∥CD,AD=BC,AC=BD.推理:AB∥CD且AD=BC,可能为等腰梯形.等腰梯形满足AC=BD,但等腰梯形不一定是矩形.结论:无法确定为矩形.
②条件:∠BAD=∠BCD=90°,AD=BC.推理:∵,∴△ABD≌△CDB(HL),∴∠ADB=∠CBD,∴AD∥BC,∴四边形ABCD为矩形.结论:确定为矩形.
③条件:∠BAD=∠BCD=90°,AC=BD.
推理:设A(0,0),D(0,a),B(b,0),C(c,d),
由∠BCD=90°,得(c﹣b)c+(d﹣a)d=0.
由AC=BD,得,联立方程可得b=0,a=d,即B(0,0),C(a,a),此时四边形为矩形.结论:必为矩形.
故选:②③.
【点睛】本题主要考查矩形的判定条件,解题的关键是结合四边形的性质进行推理.
21.如图,在三角形ABC中,点O是AC边上的一个动点,过点O作直线MN平行于BC,设MN交∠ACB的角平分线于点E,交∠ACB的外角平分线于F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
【点拨】(1)由角平分线的定义得∠ACE=∠BCE,∠ACF=∠GCF,再由平行线的性质得∠OEC=∠BCE,∠OFC=∠GCF,则∠OEC=∠ACE,∠OFC=∠ACF,然后证明EO=CO,FO=CO,即可得出结论;
(2)先证明四边形AECF是平行四边形,再证明AC=EF,然后由矩形的判定即可得出结论.
【解析】(1)证明:如图,
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠ACE=∠BCE,∠ACF=∠GCF,
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
∴∠OEC=∠ACE,∠OFC=∠ACF,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形,理由如下:
当O为AC的中点时,AO=CO,
由(1)可知,EO=FO=CO,
∴四边形AECF是平行四边形,
∵OA+OC=OE+OF,
即AC=EF,
∴平行四边形AECF是矩形.
【点睛】本题考查了矩形的判定、平行四边形的判定与性质、平行线的性质、等腰三角形的判定等知识,熟练掌握矩形的判定和等腰三角形的判定是解题的关键.
22.如图所示,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,且AB=12,BC=16.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC于点E,求∠BDF的度数.
【点拨】(1)先证明四边形ABCD是平行四边形,利用勾股定理逆定理,得到∠ABC=90°,即可得证;
(2)求出∠FDC的度数,根据三角形的内角和,求出∠DCO,然后根据OD=OC,得到∠CDO,即可求出∠BDF的度数.
【解析】(1)证明:∵在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,
∴四边形ABCD是平行四边形,AC=AO+CO=20,
∵AB=12,BC=16,
∴AB2+BC=122+162=202=AC2,
∴∠ABC=90°,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形
∴∠ADC=90°,
∵∠ADF:∠FDC=3:2,∠ADF+∠FDC=∠ADC,
∴,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
【点睛】本题考查了平行四边形的判定和性质,矩形的判定和性质,能灵活运用定理进行推理是解题的关键.注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.
23.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形 B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形 D.若CH=3,CG=4,则CE=2.5
【点拨】由∠ACB角平分线和它的外角的平分线分别交DE于点G和H可得∠HCG=90°,∠ECG=∠ACG即可得HE=EC=EG,再根据A,B,C,D的条件,进行判断.
【解析】解:∵∠ACB角平分线和它的外角的平分线分别交DE于点G和H,
∴∠HCG=90°,∠ECG=∠ACG;
∵DE∥AC.
∴∠ACG=∠HGC=∠ECG.
∴EC=EG;
同理:HE=EC,
∴HE=EC=EG=HG;
若CH∥BG,
∴∠HCG=∠BGC=90°,
∴∠EGB=∠EBG,
∴BE=EG,
∴BE=EG=HE=EC,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形;
故A正确;
若BE=CE,
∴BE=CE=HE=EG,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形,
故B正确;
若HE=EC,则不可以证明则四边形BHCG为平行四边形,
故C错误;
若CH=3,CG=4,根据勾股定理可得HG=5,
∴CE=2.5,
故D正确.
故选:C.
【点睛】本题考查了矩形的判定,平行四边形的性质和判定,关键是灵活这些判定解决问题.
24.如图,在平行四边形ABCD中,E,F分别为边AB、CD的中点,BD是对角线,AG∥BD,且AG=BD,交CB的延长线于点G,连接FG,若AD⊥BD,下列结论:①DF∥BE;②四边形ADBG是矩形;③FG=AB;④4S△BFC=S ABCD,正确的有( )
A.①②③④ B.①② C.①③ D.①②④
【点拨】①证明四边形DEBF是平行四边形即可;②根据AG∥BD且AG=DB可证四边形ADBG是平行四边形,结合AD⊥BD可证四边形ADBG是矩形;③连接DG,若FG=AB,可证FG=CD,显然不一定成立;④先证明S△BFC=S△BFD,然后结合平行四边形的性质即可求解.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E、F分别为边AB、CD的中点,
∴BE=DF,
∴四边形DEBF是平行四边形,
∴DF∥BE,故①正确;
∵AG∥DB且AG=DB,
∴四边形ADBG是平行四边形,
∵AD⊥BD,
∴四边形ADBG是矩形,故②正确;
连接DG,
∵四边形ADBG是矩形,
∴DG过点E,AB=GD.
若FG=AB,则FG=GD,显然FG与GD不相等,故③不正确;
∵四边形ABCD是平行四边形,
又∵F为边CD的中点,
∴S△BFC=S△BFD,
∴,
∴4S△BFC=S ABCD,故④正确.
综上可知,正确的有①②④,
故选:D.
【点睛】本题考查了平行四边形的判定与性质,矩形的判定与性质,以及三角形的面积公式,熟练掌握平行四边形和矩形的性质是解答本题的关键.
25.如图,在矩形ABCD中,AD=12cm,点P从点A向点D以1cm/s的速度运动,点Q以4cm/s的速度从点C出发.在B,C两点之间做往返运动,两点同时出发,点P到达点D时,两点同时停止运动,这段时间内,若以P,Q,C,D四点为顶点的四边形是矩形,那么运动时间为 或4或或12 .
【点拨】根据运动表示出DP、CQ,结合矩形的判定得到当DP=CQ时以P,Q,C,D四点为顶点的四边形是矩形列式求解即可得到答案.
【解析】解:∵四边形是ABCD矩形,
∴∠D=∠C=90°,AD=BC,
∵AD=12cm,点P从点A向点D以1cm/s的速度运动,点Q以4cm/s的速度从点C出发,在B,C两点之间做往返运动,
∴DP=12﹣t,CQ=4t或CQ=24﹣4t或4t﹣24,
∵以P,Q,C,D四点为顶点的四边形是矩形,
∴DP=CQ,
∴12﹣t=4t或12﹣t=24﹣4t或12﹣t=4t﹣24,
解得:或4或,
故答案为:或4或或12.
【点睛】本题考查了矩形的判定,掌握矩形的判定是解题的关键.
26.如图, ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)在不添加新的点和线的前提下,增加一个条件: AC⊥BD(答案不唯一). ,使得四边形AOBE是矩形,并说明理由;
(2)若AC⊥BD,OE=10,AC=16,求 ABCD的面积.
【点拨】(1)添加:AC⊥BD(答案不唯一).根据有一个角是直角的平行四边形是矩形证明即可;
(2)利用矩形的性质求出AB,再利用勾股定理求出OB,可得结论.
【解析】解:(1)添加:AC⊥BD(答案不唯一).
理由:∵BE∥AC,AE∥BD,
∴四边形AOBE是平行四边形,
∵AC⊥DB,
∴∠AOB=90°,
∴四边形AOBE是矩形;
故答案为:
(2)由(1)可知,四边形AOBE是矩形,
∴AB=OE=10,
∵四边形ABCD是平行四边形,
∴OA=OC=AC=8,
∵AC⊥BD,
∴OD=OB===6,
∴BD=12,
∴四边形ABCD的面积= AC BD=×16×12=96.
【点睛】本题考查平行四边形的性质,矩形的判定和性质,勾股定理,等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
27.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,点使CF=BE,连接AF、DE、DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,BF=10,DE=8,求AE的长.
【点拨】(1)根据平行四边形性质得AD∥BC,AD=BC,再根据CF=BE得EF=BC=AD,由此可判定四边形AEFD为平行四边形,然后再根据AE⊥BC可得出结论;
(2)根据矩形性质得AF=DE=8,再根据勾股定理的逆定理证明∠BAF=90°,然后根据三角形的面积公式即可求出AE的长.
【解析】(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵CF=BE,
∴CF+CE=BE+CE,
即EF=BC,
∴AD=EF,
又∵AD∥BC,
即AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)∵四边形AEFD是矩形,
∴AF=DE=8,
在△ABF中,AB=6,AF=8,BF=10,
∵AB2+AF2=100,BF2=100,
∴AB2+AF2=BF2,
∴△ABF为直角三角形,
即∠BAF=90°,
由三角形的面积公式得:S△ABF=BF AE=AB AF,
∴AE===4.8.
【点睛】此题主要考查了矩形的判定与性质,平行四边形的性质,熟练掌握矩形的判定与性质,平行四边形的性质是解决问题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
