浙教版八年级数学下册 第5章 特殊平行四边形 单元测试(含答案)
文档属性
| 名称 | 浙教版八年级数学下册 第5章 特殊平行四边形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 97.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 08:07:16 | ||
图片预览



文档简介
浙教版八年级下 第5章 特殊平行四边形 单元测试
一.选择题(共12小题)
1.菱形具有而矩形不具有的性质是( )
A.对边平行 B.对边相等
C.对角线相等 D.对角线互相垂直
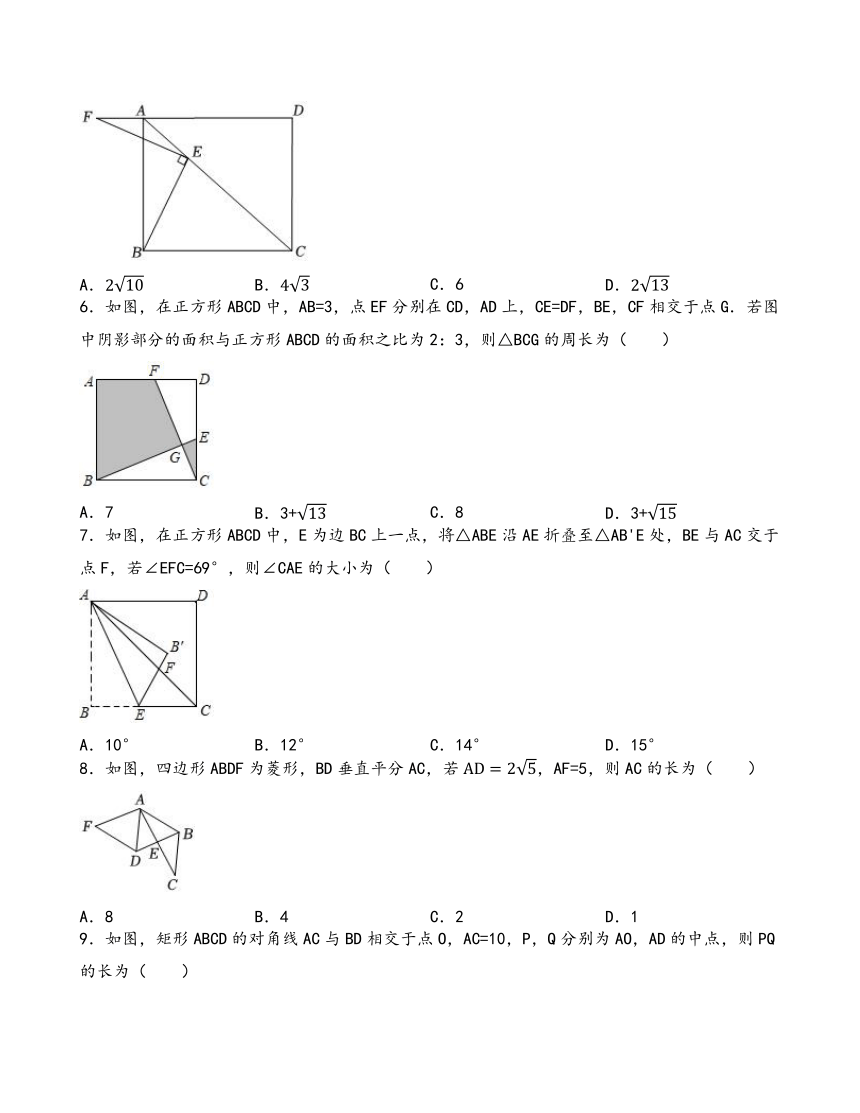
2.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1) B.(3,-1) C.(1,-3) D.(1,3)
3.如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AD,连接DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
4. ABCD中,AC,BD是两条对角线,如果添加一个条件,可推出 ABCD是菱形,那么这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BD
5.如图,已知四边形ABCD为正方形,E为对角线AC上一点,连接BE,过点E作EF⊥BE,交DA的延长线于点F,,AF=2,则BE的长为( )
A. B. C.6 D.
6.如图,在正方形ABCD中,AB=3,点EF分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为( )
A.7 B.3+ C.8 D.3+
7.如图,在正方形ABCD中,E为边BC上一点,将△ABE沿AE折叠至△AB'E处,BE与AC交于点F,若∠EFC=69°,则∠CAE的大小为( )
A.10° B.12° C.14° D.15°
8.如图,四边形ABDF为菱形,BD垂直平分AC,若,AF=5,则AC的长为( )
A.8 B.4 C.2 D.1
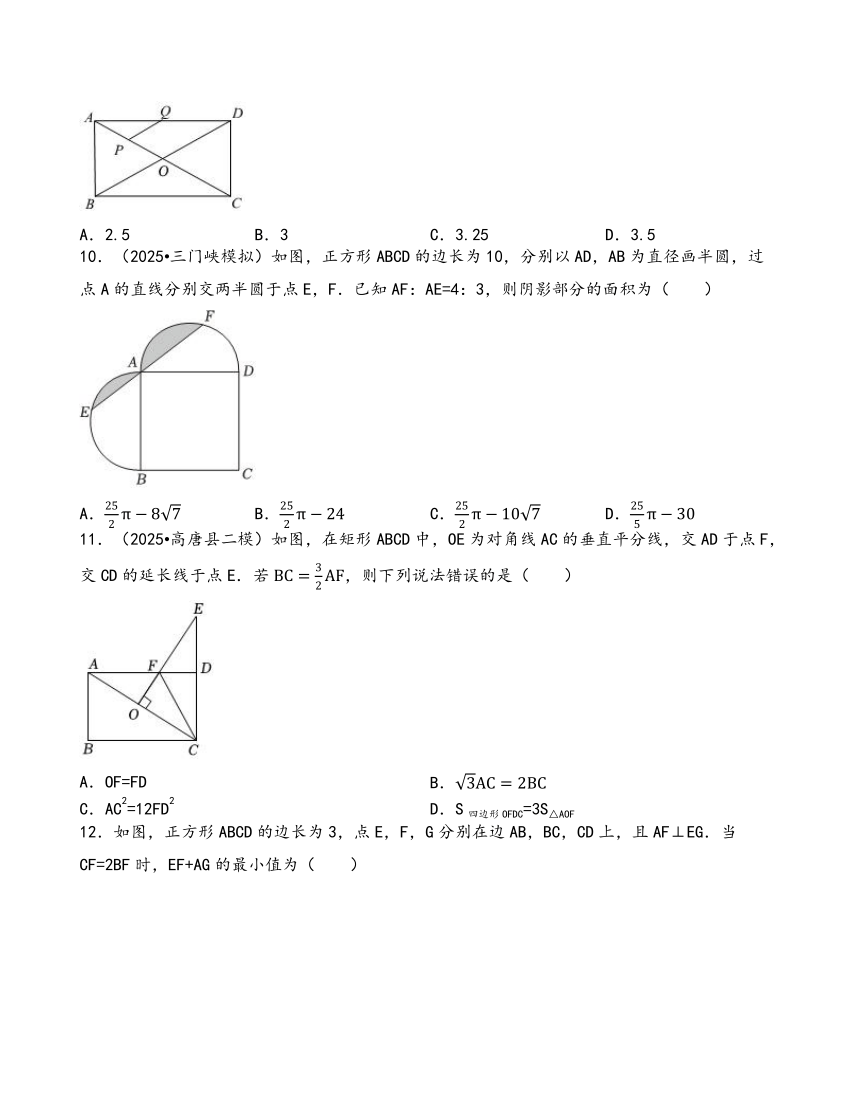
9.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长为( )
A.2.5 B.3 C.3.25 D.3.5
10.(2025 三门峡模拟)如图,正方形ABCD的边长为10,分别以AD,AB为直径画半圆,过点A的直线分别交两半圆于点E,F.已知AF:AE=4:3,则阴影部分的面积为( )
A. B. C. D.
11.(2025 高唐县二模)如图,在矩形ABCD中,OE为对角线AC的垂直平分线,交AD于点F,交CD的延长线于点E.若,则下列说法错误的是( )
A.OF=FD B.
C.AC2=12FD2 D.S四边形OFDC=3S△AOF
12.如图,正方形ABCD的边长为3,点E,F,G分别在边AB,BC,CD上,且AF⊥EG.当CF=2BF时,EF+AG的最小值为( )
A. B. C. D.
二.填空题(共5小题)
13.面积为24的菱形的一条对角线长为6,则这个菱形的边长为 ______.
14.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=2,∠ABE=45°,则DE的长是______.
15.如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 ______.
16.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为 ______.
17.(2025 青岛二模)如图,在矩形ABCD中,AB=6,BC=8,E是BC边上一点,点F在CD边的延长线上,且BE=DF,连接EF交AD边于点G,MN垂直平分EF,分别交AD,EF,CD于点N,H,M.若BE=2,则MN的长为______.
三.解答题(共5小题)
18.如图,菱形ABCD对角线AC与BD的交于点O,CD=10,OD=6,过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)则OC的长 ______.
(2)求证:四边形OBEC是矩形.
19.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=6,OE=4,∠BAE=∠DEF,求BF、DF的长.
20.如图所示,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
(1)求证:OE=CB;
(2)如果OC:OB=1:2,OE=2,求菱形ABCD的面积.
21.如图1,矩形ABCD中,AB=2,BC=3,过对角线AC中点O的直线分别交边BC、AD于点E、F
(1)求证:四边形AECF是平行四边形;
(2)如图2,当EF⊥AC时,求EF的长度.
22.如图,矩形ABCD的对角线AC与BD交于点O,点E是CD的中点,连接AE交BD于点F,延长AE到点P,使FP=AF,连接CF,CP,DP.
(1)求证:四边形CFDP是平行四边形;
(2)若四边形CFDP是矩形,且,求AB的长度.
浙教版八年级下 第5章 特殊平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、B 3、B 4、C 5、D 6、D 7、B 8、A 9、A 10、B 11、D 12、C
二.填空题(共5小题)
13、5; 14、; 15、; 16、24; 17、;
三.解答题(共5小题)
18、(1)解:∵菱形ABCD对角线AC与BD的交于点O,
∴AC⊥BD,
在Rt△COD中,CD=10,OD=6,则由勾股定理可得,
故答案为:8;
(2)证明:∵CE∥DB,BE∥AC,
∴四边形OBEC是平行四边形,
由(1)知AC⊥BD,即∠BOC=90°,
∴四边形OBEC是矩形.
19、(1)证明:∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:∵四边形AEFD为矩形,
∴,
∴AF=DE=2OE=8,OA=OF=OD=OE,
∴∠DEF=∠AFE,
又∵∠AEF=90°,
∴∠EAF+∠AFE=90°,
又∵∠BAE=∠DEF,∠DEF=∠AFE,
∴∠BAE+∠EAF=90°,
∴∠BAF=90°,
在Rt△BAF中,由勾股定理得:BF2=AB2+AF2=62+82=100,
∴BF=10,
∵,
∴,
解得AE=4.8,
∴DF=AE=4.8.
20、(1)证明:∵CE∥BD,EB∥AC,
∴四边形OBEC为平行四边形.
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠BOC=90°,
∴四边形OBEC为矩形,
∴OE=CB.
(2)解:设OC=x,则OB=2x,
∴BC==x.
∵BC=OE=2,
∴x=2,
∴OC=2,OB=4,
∴S菱形ABCD=AC BD=2OC OB=16.
21、解:∵矩形ABCD,∴AF∥EC,AO=CO
∴∠FAO=∠ECO
∴在△AOF和△COE中,,
∴△AOF≌△COE(ASA)
∴AF=EC
又∵AF∥EC
∴四边形AECF是平行四边形;
(2)由(1)知四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形,
设BE=a,则AE=EC=3-a
∴a2+22=(3-a)2
∴a=
则AE=EC=,
∵AB=2,BC=3,
∴AC==
∴AO=OC=,
∴OE===,
∴EF=2OF=.
22、(1)证明:∵四边形ABCD是矩形,
∴AO=CO,
∵FP=AF,
∴OF是△ACP的中位线,
∴OF∥CP,
∴∠FDE=∠PCE(两直线平行,内错角相等),
∵点E是CD的中点,
∴DE=CE,
在△DEF和△CEP中,
,
∴△DEF≌△CEP(ASA),
∴EF=EP,
又∵DE=CE,
∴四边形CFDP是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB,∠ADE=90°,
∴根据勾股定理,AD2+DE2=AE2,
若四边形CFDP是矩形,则,
,FP=CD,
∵AF=FP,
∴,
∴,
∴AD2=2CD2,
∴或(不符合题意,舍去),
∵,
∴CD=AB=1,所以AB的长度为1.
一.选择题(共12小题)
1.菱形具有而矩形不具有的性质是( )
A.对边平行 B.对边相等
C.对角线相等 D.对角线互相垂直
2.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1) B.(3,-1) C.(1,-3) D.(1,3)
3.如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AD,连接DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
4. ABCD中,AC,BD是两条对角线,如果添加一个条件,可推出 ABCD是菱形,那么这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BD
5.如图,已知四边形ABCD为正方形,E为对角线AC上一点,连接BE,过点E作EF⊥BE,交DA的延长线于点F,,AF=2,则BE的长为( )
A. B. C.6 D.
6.如图,在正方形ABCD中,AB=3,点EF分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为( )
A.7 B.3+ C.8 D.3+
7.如图,在正方形ABCD中,E为边BC上一点,将△ABE沿AE折叠至△AB'E处,BE与AC交于点F,若∠EFC=69°,则∠CAE的大小为( )
A.10° B.12° C.14° D.15°
8.如图,四边形ABDF为菱形,BD垂直平分AC,若,AF=5,则AC的长为( )
A.8 B.4 C.2 D.1
9.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长为( )
A.2.5 B.3 C.3.25 D.3.5
10.(2025 三门峡模拟)如图,正方形ABCD的边长为10,分别以AD,AB为直径画半圆,过点A的直线分别交两半圆于点E,F.已知AF:AE=4:3,则阴影部分的面积为( )
A. B. C. D.
11.(2025 高唐县二模)如图,在矩形ABCD中,OE为对角线AC的垂直平分线,交AD于点F,交CD的延长线于点E.若,则下列说法错误的是( )
A.OF=FD B.
C.AC2=12FD2 D.S四边形OFDC=3S△AOF
12.如图,正方形ABCD的边长为3,点E,F,G分别在边AB,BC,CD上,且AF⊥EG.当CF=2BF时,EF+AG的最小值为( )
A. B. C. D.
二.填空题(共5小题)
13.面积为24的菱形的一条对角线长为6,则这个菱形的边长为 ______.
14.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=2,∠ABE=45°,则DE的长是______.
15.如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 ______.
16.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为 ______.
17.(2025 青岛二模)如图,在矩形ABCD中,AB=6,BC=8,E是BC边上一点,点F在CD边的延长线上,且BE=DF,连接EF交AD边于点G,MN垂直平分EF,分别交AD,EF,CD于点N,H,M.若BE=2,则MN的长为______.
三.解答题(共5小题)
18.如图,菱形ABCD对角线AC与BD的交于点O,CD=10,OD=6,过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)则OC的长 ______.
(2)求证:四边形OBEC是矩形.
19.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=6,OE=4,∠BAE=∠DEF,求BF、DF的长.
20.如图所示,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
(1)求证:OE=CB;
(2)如果OC:OB=1:2,OE=2,求菱形ABCD的面积.
21.如图1,矩形ABCD中,AB=2,BC=3,过对角线AC中点O的直线分别交边BC、AD于点E、F
(1)求证:四边形AECF是平行四边形;
(2)如图2,当EF⊥AC时,求EF的长度.
22.如图,矩形ABCD的对角线AC与BD交于点O,点E是CD的中点,连接AE交BD于点F,延长AE到点P,使FP=AF,连接CF,CP,DP.
(1)求证:四边形CFDP是平行四边形;
(2)若四边形CFDP是矩形,且,求AB的长度.
浙教版八年级下 第5章 特殊平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、B 3、B 4、C 5、D 6、D 7、B 8、A 9、A 10、B 11、D 12、C
二.填空题(共5小题)
13、5; 14、; 15、; 16、24; 17、;
三.解答题(共5小题)
18、(1)解:∵菱形ABCD对角线AC与BD的交于点O,
∴AC⊥BD,
在Rt△COD中,CD=10,OD=6,则由勾股定理可得,
故答案为:8;
(2)证明:∵CE∥DB,BE∥AC,
∴四边形OBEC是平行四边形,
由(1)知AC⊥BD,即∠BOC=90°,
∴四边形OBEC是矩形.
19、(1)证明:∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:∵四边形AEFD为矩形,
∴,
∴AF=DE=2OE=8,OA=OF=OD=OE,
∴∠DEF=∠AFE,
又∵∠AEF=90°,
∴∠EAF+∠AFE=90°,
又∵∠BAE=∠DEF,∠DEF=∠AFE,
∴∠BAE+∠EAF=90°,
∴∠BAF=90°,
在Rt△BAF中,由勾股定理得:BF2=AB2+AF2=62+82=100,
∴BF=10,
∵,
∴,
解得AE=4.8,
∴DF=AE=4.8.
20、(1)证明:∵CE∥BD,EB∥AC,
∴四边形OBEC为平行四边形.
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠BOC=90°,
∴四边形OBEC为矩形,
∴OE=CB.
(2)解:设OC=x,则OB=2x,
∴BC==x.
∵BC=OE=2,
∴x=2,
∴OC=2,OB=4,
∴S菱形ABCD=AC BD=2OC OB=16.
21、解:∵矩形ABCD,∴AF∥EC,AO=CO
∴∠FAO=∠ECO
∴在△AOF和△COE中,,
∴△AOF≌△COE(ASA)
∴AF=EC
又∵AF∥EC
∴四边形AECF是平行四边形;
(2)由(1)知四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形,
设BE=a,则AE=EC=3-a
∴a2+22=(3-a)2
∴a=
则AE=EC=,
∵AB=2,BC=3,
∴AC==
∴AO=OC=,
∴OE===,
∴EF=2OF=.
22、(1)证明:∵四边形ABCD是矩形,
∴AO=CO,
∵FP=AF,
∴OF是△ACP的中位线,
∴OF∥CP,
∴∠FDE=∠PCE(两直线平行,内错角相等),
∵点E是CD的中点,
∴DE=CE,
在△DEF和△CEP中,
,
∴△DEF≌△CEP(ASA),
∴EF=EP,
又∵DE=CE,
∴四边形CFDP是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB,∠ADE=90°,
∴根据勾股定理,AD2+DE2=AE2,
若四边形CFDP是矩形,则,
,FP=CD,
∵AF=FP,
∴,
∴,
∴AD2=2CD2,
∴或(不符合题意,舍去),
∵,
∴CD=AB=1,所以AB的长度为1.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
