解直角三角形(复习)
图片预览




文档简介
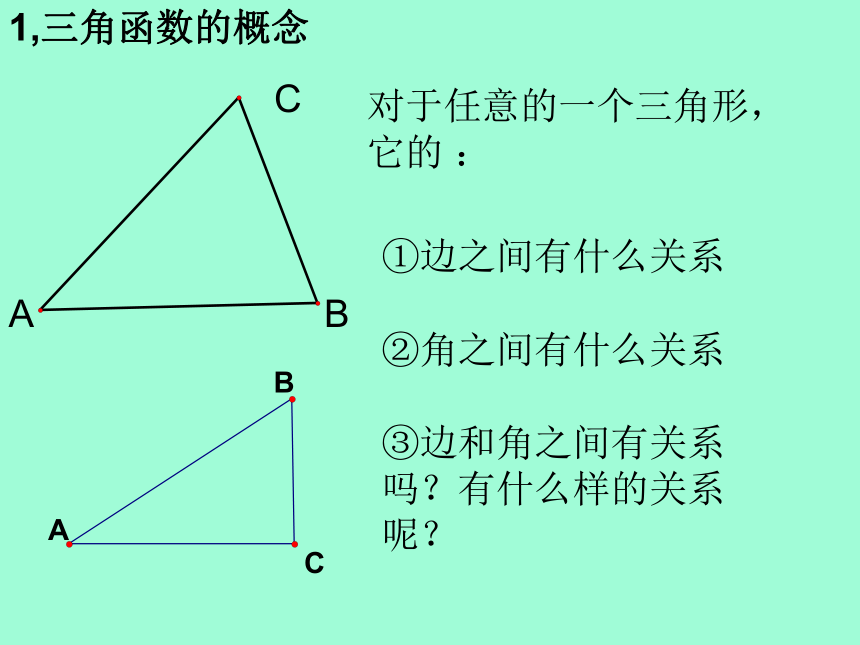
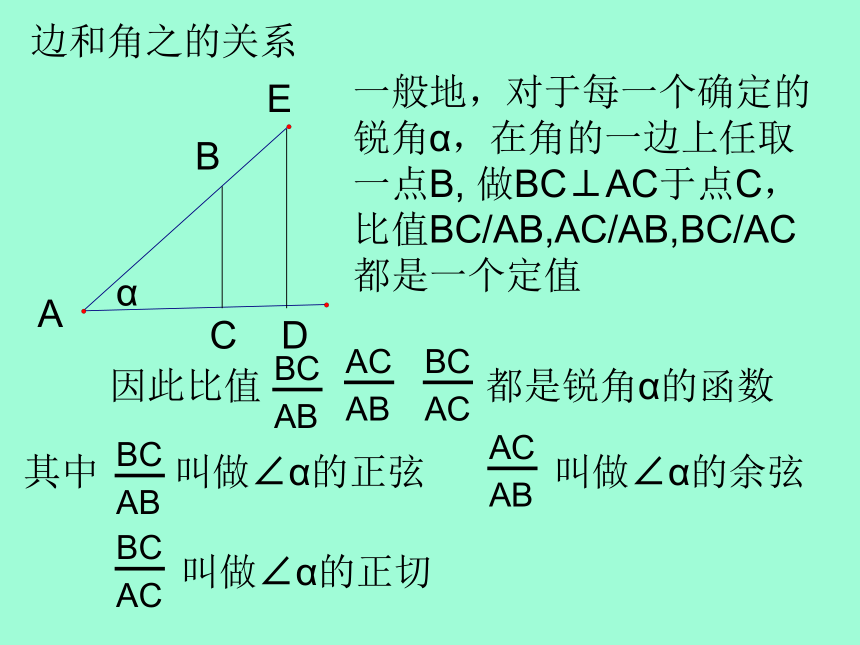
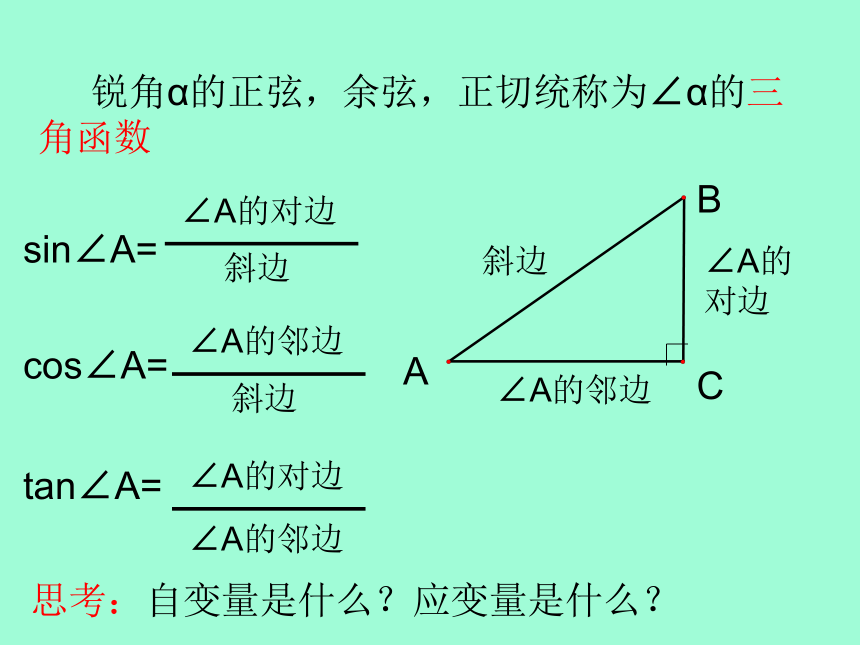
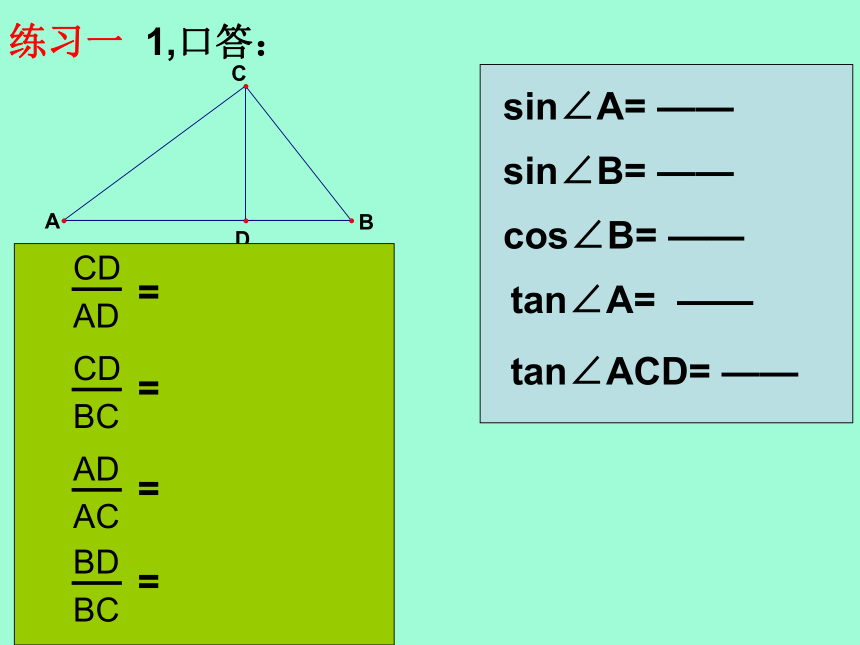
课件23张PPT。解直角三角形1,三角函数的概念2,特殊锐角的三角函数(30°.45°.60°)3,一般锐角的三角函数(0°< α <90°)4,解直角三角形1,三角函数的概念边和角之的关系ABCDE一般地,对于每一个确定的锐角α,在角的一边上任取一点B, 做BC⊥AC于点C,比值BC/AB,AC/AB,BC/AC都是一个定值α 锐角α的正弦,余弦,正切统称为∠α的三角函数ABC斜边∠A的对边∠A的邻边sin∠A=cos∠A=tan∠A=思考:自变量是什么?应变量是什么?练习一1,口答:2,在Rt△ABC中 ,∠C为直角,AB=13,AC=12,求∠B的正弦,余弦,正切.解,由勾股定理得
BC=55注意:一些特殊的直角三角形应熟记
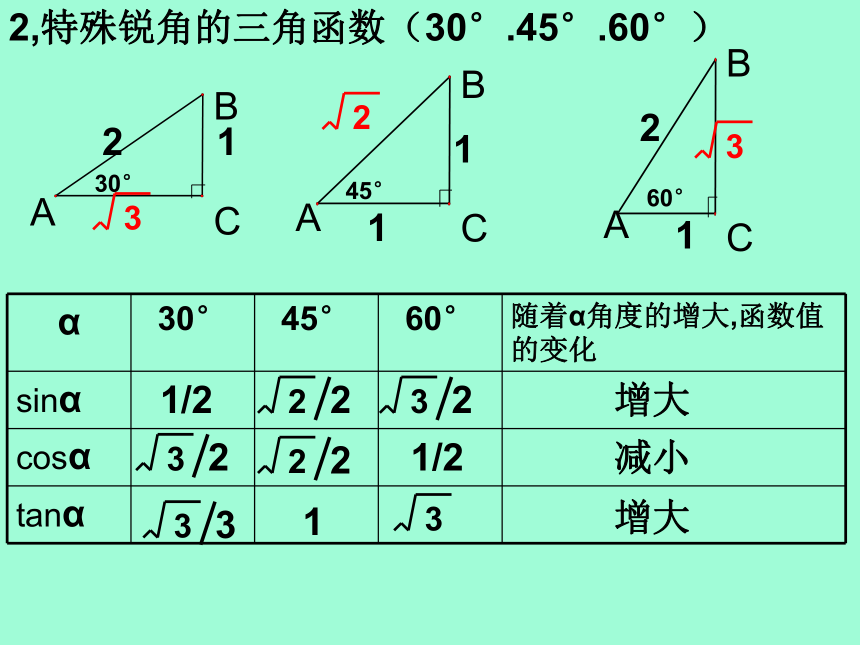
(3.4.5)(5.12.13)(1.2._)(1.1._)2,特殊锐角的三角函数(30°.45°.60°)21111230°45°60°增大增大减小练习二1,背诵这三个角的三角函数(1分钟)2,看谁的反应最快!sin60°=sin30°=tan60°=cos30°=cos60°=tan30°=记忆方法: ①画图法 ②增减性sin60°=cos45°=cos30°=tan60°=12,计算① sin30°___sin45°___sin60°
cos30°___cos45°___cos60°
cos30°___cos45°___cos60°(>,<)②sin60°+ cos30° ③sin260°④sin260°+tan45°-8cos230°3,若sin∠A= ,那么∠A=____ °
若 cos∠A= ,那么∠A=____ °
若 tan ∠A= ,那么∠A=____ °3,一般锐角的三角函数(0°< α <90°)(思想方法:由特殊到一般)sin55°=tan55°17′45″=…12(1+sin35°+cos35°) =…已知sinα=0.278,求锐角α的度数.已知cosα=0.7875,求锐角α的度数.练习三(借助计算器)①sin25°+cos65° tan56°·cos65°②把下列余弦值按从小到大的顺序排列
cos57°18′ cos27°12′ cos89°62′
③已知有一个以12,16,20为边长的三角形,求这个三角形最小角的度数.变形为:已知sin ∠A= 3/5,求∠A4,解直角三角形 在直角三角形中,由已知的一些边和角,求出另一些边和角的过程,就叫解直角三角形例1,在Rt△ABC中, ∠C= Rt ∠,AB=3 , ∠A=52°求∠B和a,b1,已知几个角,几条边,求几个角,几条边?2,∠B怎么求?3,a怎么求?选用哪种三角函数4,b怎么求?选用哪种三角函数知一边一锐角解直角三角形知两边解直角三角形知两个锐角解直角三角形例2,已知红领巾的边AC的长为50cm, ∠A= 37 ° (精确到0.1)50cm37 °(等腰三角形)1,求红领巾的周长2,求红领巾的面积(梯形)例3∠C叫做坡角
tan ∠C叫做坡度(坡比)(任意三角形)例57930 °1,该三角形的周长可求吗?为多少?2,该三角形的面积可求吗?为多少?α3,求三角形面积的新公式:S△ =1/2sin ∠Abc练习四1,在Rt △ABC中, ∠C为Rt ∠⑴已知∠A和c,则a=____ b=____
⑵已知∠B和b,则a=____ c=____
△ABC的面积S=_____________
2, 求下列三角形的面积5845 °解: S△ =1/2acsin ∠B
=1/2×5×8×sin45°
=D60°3、如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40∴CD=20, AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,∴S△ABC= AB?CD= (AD+DB)?CD再见1,三角函数的概念2,特殊锐角的三角函数(30°.45°.60°)3,一般锐角的三角函数(0°< α <90°)4,解直角三角形解直角三角形
BC=55注意:一些特殊的直角三角形应熟记
(3.4.5)(5.12.13)(1.2._)(1.1._)2,特殊锐角的三角函数(30°.45°.60°)21111230°45°60°增大增大减小练习二1,背诵这三个角的三角函数(1分钟)2,看谁的反应最快!sin60°=sin30°=tan60°=cos30°=cos60°=tan30°=记忆方法: ①画图法 ②增减性sin60°=cos45°=cos30°=tan60°=12,计算① sin30°___sin45°___sin60°
cos30°___cos45°___cos60°
cos30°___cos45°___cos60°(>,<)②sin60°+ cos30° ③sin260°④sin260°+tan45°-8cos230°3,若sin∠A= ,那么∠A=____ °
若 cos∠A= ,那么∠A=____ °
若 tan ∠A= ,那么∠A=____ °3,一般锐角的三角函数(0°< α <90°)(思想方法:由特殊到一般)sin55°=tan55°17′45″=…12(1+sin35°+cos35°) =…已知sinα=0.278,求锐角α的度数.已知cosα=0.7875,求锐角α的度数.练习三(借助计算器)①sin25°+cos65° tan56°·cos65°②把下列余弦值按从小到大的顺序排列
cos57°18′ cos27°12′ cos89°62′
③已知有一个以12,16,20为边长的三角形,求这个三角形最小角的度数.变形为:已知sin ∠A= 3/5,求∠A4,解直角三角形 在直角三角形中,由已知的一些边和角,求出另一些边和角的过程,就叫解直角三角形例1,在Rt△ABC中, ∠C= Rt ∠,AB=3 , ∠A=52°求∠B和a,b1,已知几个角,几条边,求几个角,几条边?2,∠B怎么求?3,a怎么求?选用哪种三角函数4,b怎么求?选用哪种三角函数知一边一锐角解直角三角形知两边解直角三角形知两个锐角解直角三角形例2,已知红领巾的边AC的长为50cm, ∠A= 37 ° (精确到0.1)50cm37 °(等腰三角形)1,求红领巾的周长2,求红领巾的面积(梯形)例3∠C叫做坡角
tan ∠C叫做坡度(坡比)(任意三角形)例57930 °1,该三角形的周长可求吗?为多少?2,该三角形的面积可求吗?为多少?α3,求三角形面积的新公式:S△ =1/2sin ∠Abc练习四1,在Rt △ABC中, ∠C为Rt ∠⑴已知∠A和c,则a=____ b=____
⑵已知∠B和b,则a=____ c=____
△ABC的面积S=_____________
2, 求下列三角形的面积5845 °解: S△ =1/2acsin ∠B
=1/2×5×8×sin45°
=D60°3、如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40∴CD=20, AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,∴S△ABC= AB?CD= (AD+DB)?CD再见1,三角函数的概念2,特殊锐角的三角函数(30°.45°.60°)3,一般锐角的三角函数(0°< α <90°)4,解直角三角形解直角三角形
