初中数学浙教版九年级上册 4.1 比例线段 同步学案(含简单答案)
文档属性
| 名称 | 初中数学浙教版九年级上册 4.1 比例线段 同步学案(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 299.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 16:34:23 | ||
图片预览



文档简介
4.1 比例线段
一、知识点1 比例的基本性质
1.已知,则下列比例式成立的是( )
A. B. C. D.
2.若,则的值是( )
A. B. C. D.
3.已知,则 .
4.已知,,是的三边长,且,,求的周长.
二、知识点2 比例线段及比例尺
5.下列各组中的四条线段成比例的是( )
A.a=2,b=3,c=4,d=1 B.a=2, b=, c=,d=
C.a=4,b=6,c=5,d=10 D.a=,b=3,c=2,d=
6.已知,,,成比例线段.若,,,则的长为( )
A. B. C. D.
7.如果在比例尺为的地图上,、两地的图上距离是46厘米,那么、两地的实际距离是 千米.
8.如图有3个已知边长的矩形,分别记为图甲、图乙、图丙.
(1)填写两个长与宽成比例的矩形:图______和图______.(填“甲”或“乙”或“丙”)
(2)改变(1)中未被选择矩形的一边长,使之与(1)中矩形的长与宽成比例,请给出一种更改方案,并说明理由.
三、知识点3 比例中项
9.已知两条线段的长分别为3cm和12cm,则它们的比例中项是( )
A.4cm B.6cm C.9cm D.36cm
10.已知线段a是线段b,c的比例中项,则( )
A. B. C. D.
11.小明利用杠杆原理称药品质量,其知识是“杠杆平衡时,动力动力臂阻力阻力臂”.如图,当质量为m克的药品分别放在左盘、右盘时,另外一盘分别放了重20克、5克的砝码时杠杆平衡,则m的值为 .
12.已知线段满足,且.
(1)求线段的长.
(2)若线段是线段的比例中项,求线段的长.
四、知识点4 黄金分割
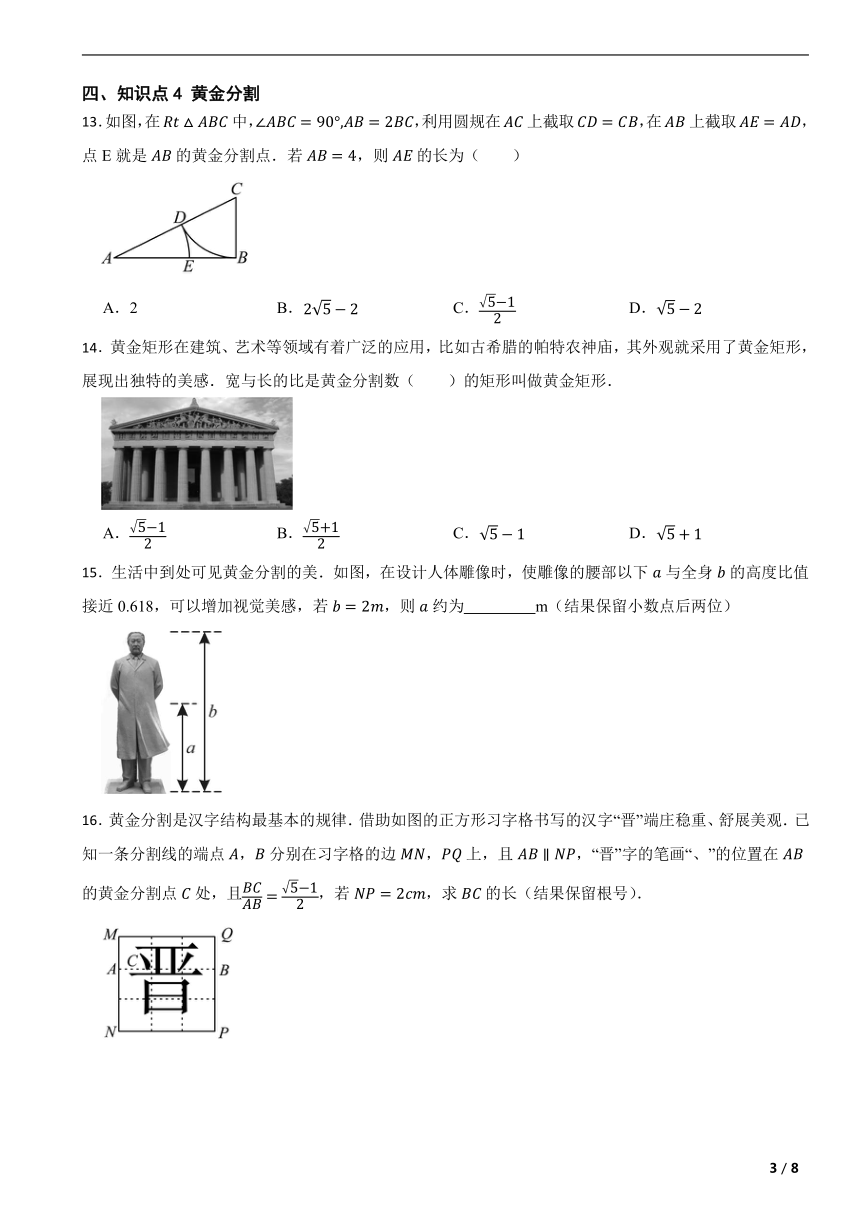
13.如图,在中,,利用圆规在上截取,在上截取,点E就是的黄金分割点.若,则的长为( )
A.2 B. C. D.
14.黄金矩形在建筑、艺术等领域有着广泛的应用,比如古希腊的帕特农神庙,其外观就采用了黄金矩形,展现出独特的美感.宽与长的比是黄金分割数( )的矩形叫做黄金矩形.
A. B. C. D.
15.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下与全身的高度比值接近0.618,可以增加视觉美感,若,则约为 m(结果保留小数点后两位)
16.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点,分别在习字格的边,上,且,“晋”字的笔画“、”的位置在的黄金分割点处,且,若,求的长(结果保留根号).
五、课后练习
17.若,则下列比例式中正确的是( )
A. B. C. D.
18.下列各组线段,能成比例的是( )
A.,,, B.,,, C.,,, D.,,,
19.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,为的黄金分割点,如果的长度为,则的长度是( )
A. B. C. D.
20.如图,在四边形ABCD中,∠DAB=∠CBA=90°,E为边AB的黄金分割点(AE>BE),AD=AE,BC=BE.AC,DE将四边形分为四个部分,它们的面积分别用S1,S2,S3,S4表示,则下列判断正确的是( )
A.S1=4S2 B.S4=3S2 C.S1=S3 D.S3=S4
21.若,则的值为 .
22.如图,顶角为的等腰三角形,其底边与腰之比等于k,这样的三角形称为黄金三角形,已知腰,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形以此类推,第2022个黄金三角形的周长
23.在比例尺为的地图上,测得一个多边形地块的面积为,则这个多边形地块的实际面积是 (结果用科学记数法表示).
24.如图,□ABCD 的对角线AC,BD交于点O,且,AE平分∠BAD,交 BC边于点E,连接OE,若,则n为 .
25.(1)已知,求x:y的值.
(2)已知线段a=2,b=8,求线段a,b的比例中项.
26.如图,在线段AB上存在一点C,满足AC:CB=CB:AB=k.
(1)求k的值.
(2)若三条线段a,b,c满足a:b=b:c=k,问:这三条线段能否首尾相接构成一个三角形?如果能,指出三角形的形状;如果不能,请说明理由.
27.综合与实践.实践主题:黄金分割数.
(1)材料探索:如图1,我们知道,如果点P是线段上的一点,将线段分割成,两条线段,且满足,那么这种分割就叫做黄金分割.其中线段与的比值或线段与的比值叫做黄金分割数.
若设线段,的长为x,则可表示为,
∵, ∴,
…,根据此方法可计算出黄金分割数为_____________(结果保留根号).
(2)实践应用:二胡是中国古老的民族拉弦乐器之一,演奏家发现,二胡的“千斤”钩在琴弦长的黄金分割点处(“千斤”上面一截琴弦比下面一截琴弦短),奏出来的音调最和谐悦耳.如图2,一把二胡的琴弦长为,求“千斤”下面一截琴弦长(结果保留根号).
参考答案
1.B
2.B
3.
4.的周长为18.
5.B
6.B
7.
8.(1)甲,丙;
(2)图乙中,长减少7时,与(1)中矩形的长与宽成比例.
9.B
10.B
11.10
12.(1)线段的长为12,线段的长为3.
(2)线段的长为6.
13.B
14.A
15.1.24
16.
17.D
18.A
19.A
20.C
21.
22.
23.
24.
25.(1)x:y=3:4
(2)c=4.
26.(1)k=;
(2)解:线段a,b,c不能首尾相接构成一个三角形,理由如下:
∵a : b=b: c=k,
∴b=kc=c,a=kb=()2c=c
∵a+b=c,
∴线段a,b,c不能构成三角形.
27.(1)
(2)
1 / 1
一、知识点1 比例的基本性质
1.已知,则下列比例式成立的是( )
A. B. C. D.
2.若,则的值是( )
A. B. C. D.
3.已知,则 .
4.已知,,是的三边长,且,,求的周长.
二、知识点2 比例线段及比例尺
5.下列各组中的四条线段成比例的是( )
A.a=2,b=3,c=4,d=1 B.a=2, b=, c=,d=
C.a=4,b=6,c=5,d=10 D.a=,b=3,c=2,d=
6.已知,,,成比例线段.若,,,则的长为( )
A. B. C. D.
7.如果在比例尺为的地图上,、两地的图上距离是46厘米,那么、两地的实际距离是 千米.
8.如图有3个已知边长的矩形,分别记为图甲、图乙、图丙.
(1)填写两个长与宽成比例的矩形:图______和图______.(填“甲”或“乙”或“丙”)
(2)改变(1)中未被选择矩形的一边长,使之与(1)中矩形的长与宽成比例,请给出一种更改方案,并说明理由.
三、知识点3 比例中项
9.已知两条线段的长分别为3cm和12cm,则它们的比例中项是( )
A.4cm B.6cm C.9cm D.36cm
10.已知线段a是线段b,c的比例中项,则( )
A. B. C. D.
11.小明利用杠杆原理称药品质量,其知识是“杠杆平衡时,动力动力臂阻力阻力臂”.如图,当质量为m克的药品分别放在左盘、右盘时,另外一盘分别放了重20克、5克的砝码时杠杆平衡,则m的值为 .
12.已知线段满足,且.
(1)求线段的长.
(2)若线段是线段的比例中项,求线段的长.
四、知识点4 黄金分割
13.如图,在中,,利用圆规在上截取,在上截取,点E就是的黄金分割点.若,则的长为( )
A.2 B. C. D.
14.黄金矩形在建筑、艺术等领域有着广泛的应用,比如古希腊的帕特农神庙,其外观就采用了黄金矩形,展现出独特的美感.宽与长的比是黄金分割数( )的矩形叫做黄金矩形.
A. B. C. D.
15.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下与全身的高度比值接近0.618,可以增加视觉美感,若,则约为 m(结果保留小数点后两位)
16.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点,分别在习字格的边,上,且,“晋”字的笔画“、”的位置在的黄金分割点处,且,若,求的长(结果保留根号).
五、课后练习
17.若,则下列比例式中正确的是( )
A. B. C. D.
18.下列各组线段,能成比例的是( )
A.,,, B.,,, C.,,, D.,,,
19.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,为的黄金分割点,如果的长度为,则的长度是( )
A. B. C. D.
20.如图,在四边形ABCD中,∠DAB=∠CBA=90°,E为边AB的黄金分割点(AE>BE),AD=AE,BC=BE.AC,DE将四边形分为四个部分,它们的面积分别用S1,S2,S3,S4表示,则下列判断正确的是( )
A.S1=4S2 B.S4=3S2 C.S1=S3 D.S3=S4
21.若,则的值为 .
22.如图,顶角为的等腰三角形,其底边与腰之比等于k,这样的三角形称为黄金三角形,已知腰,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形以此类推,第2022个黄金三角形的周长
23.在比例尺为的地图上,测得一个多边形地块的面积为,则这个多边形地块的实际面积是 (结果用科学记数法表示).
24.如图,□ABCD 的对角线AC,BD交于点O,且,AE平分∠BAD,交 BC边于点E,连接OE,若,则n为 .
25.(1)已知,求x:y的值.
(2)已知线段a=2,b=8,求线段a,b的比例中项.
26.如图,在线段AB上存在一点C,满足AC:CB=CB:AB=k.
(1)求k的值.
(2)若三条线段a,b,c满足a:b=b:c=k,问:这三条线段能否首尾相接构成一个三角形?如果能,指出三角形的形状;如果不能,请说明理由.
27.综合与实践.实践主题:黄金分割数.
(1)材料探索:如图1,我们知道,如果点P是线段上的一点,将线段分割成,两条线段,且满足,那么这种分割就叫做黄金分割.其中线段与的比值或线段与的比值叫做黄金分割数.
若设线段,的长为x,则可表示为,
∵, ∴,
…,根据此方法可计算出黄金分割数为_____________(结果保留根号).
(2)实践应用:二胡是中国古老的民族拉弦乐器之一,演奏家发现,二胡的“千斤”钩在琴弦长的黄金分割点处(“千斤”上面一截琴弦比下面一截琴弦短),奏出来的音调最和谐悦耳.如图2,一把二胡的琴弦长为,求“千斤”下面一截琴弦长(结果保留根号).
参考答案
1.B
2.B
3.
4.的周长为18.
5.B
6.B
7.
8.(1)甲,丙;
(2)图乙中,长减少7时,与(1)中矩形的长与宽成比例.
9.B
10.B
11.10
12.(1)线段的长为12,线段的长为3.
(2)线段的长为6.
13.B
14.A
15.1.24
16.
17.D
18.A
19.A
20.C
21.
22.
23.
24.
25.(1)x:y=3:4
(2)c=4.
26.(1)k=;
(2)解:线段a,b,c不能首尾相接构成一个三角形,理由如下:
∵a : b=b: c=k,
∴b=kc=c,a=kb=()2c=c
∵a+b=c,
∴线段a,b,c不能构成三角形.
27.(1)
(2)
1 / 1
同课章节目录
