6.3 反比例函数的应用(含解析)-2024-2025学年浙教版八年级下册 同步分层作业
文档属性
| 名称 | 6.3 反比例函数的应用(含解析)-2024-2025学年浙教版八年级下册 同步分层作业 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.3 反比例函数的应用 同步分层作业
1.如图,点P在反比例函数图象上,PA⊥x轴于点A,若△POA的面积等于3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
2.根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2 C.S小于10m2 D.S大于10m2
3.如图,函数y1=x﹣1和函数的图象相交于点M(m,1),N(n,﹣2),若y1<y2,则x的取值范围是( )
A.﹣1<x<2 B.x<﹣1或0<x<2 C.﹣1<x<0或0<x<2 D.﹣1<x<0或x>2
4.某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流I(A)与电阻R(Ω)的关系图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A.当I=0.2时,R=1000 B.I与R的函数表达式是
C.当R>500时,I>0.44 D.当880<R<1000时,则0.22<I<0.25
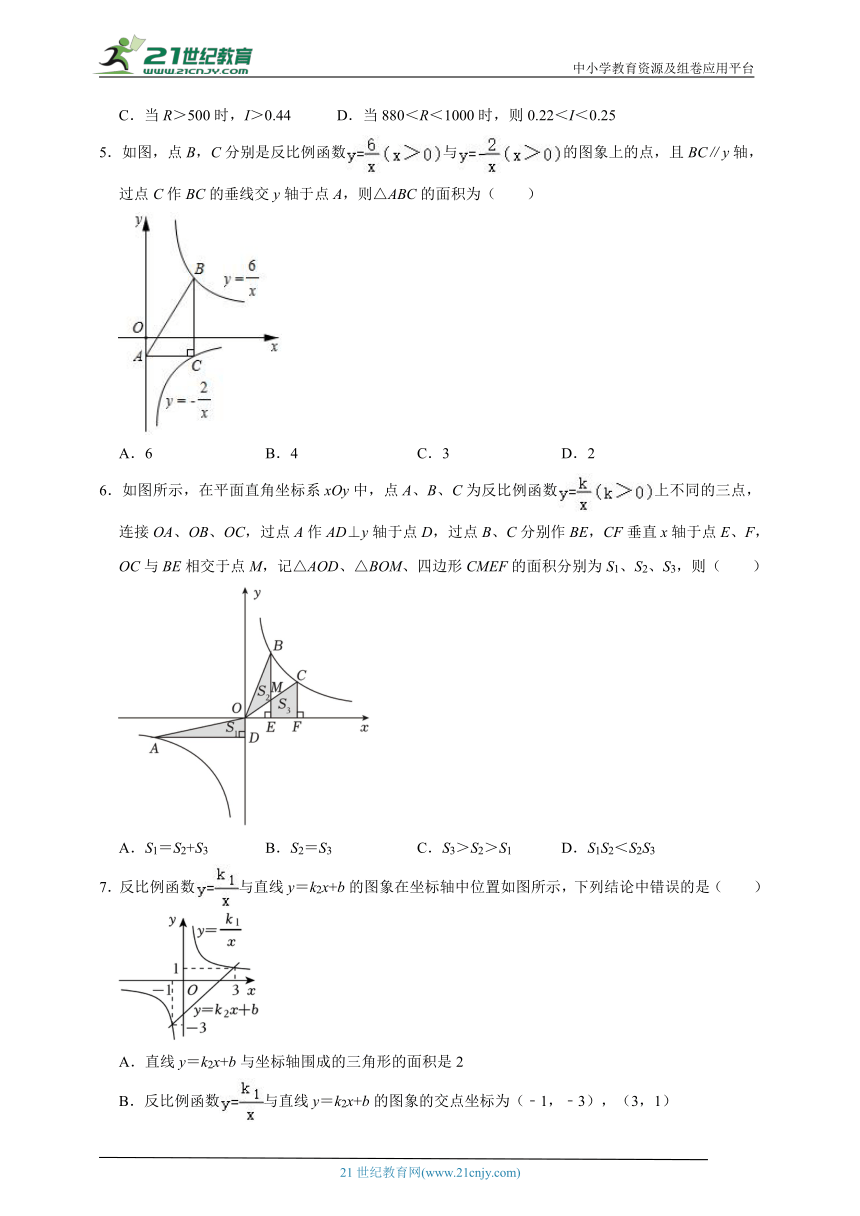
5.如图,点B,C分别是反比例函数与的图象上的点,且BC∥y轴,过点C作BC的垂线交y轴于点A,则△ABC的面积为( )
A.6 B.4 C.3 D.2
6.如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
A.S1=S2+S3 B.S2=S3 C.S3>S2>S1 D.S1S2<S2S3
7.反比例函数与直线y=k2x+b的图象在坐标轴中位置如图所示,下列结论中错误的是( )
A.直线y=k2x+b与坐标轴围成的三角形的面积是2
B.反比例函数与直线y=k2x+b的图象的交点坐标为(﹣1,﹣3),(3,1)
C.b<0<k2<k1
D.当﹣1<x<3时,有
8.已知反比例函数与正比例函数y=2x图象的一个交点坐标为(2,4),则另一个交点坐标为 .
9.一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=20m3时,ρ=1.36kg/m3,当V=40m3时,ρ= kg/m3.
10.如图,小华设计了一个探索杠杆平衡条件的实验,在一根匀质的木杆中点O处用一根细绳挂在支架上,在点O的左侧固定位置B处悬挂重物A,在点O的右侧用一个弹簧测力计向下拉木杆,使木杆达到平衡(杠杆平衡时,动力×动力臂=阻力×阻力臂).改变弹簧测力计与点O的距离x(单位:cm),观察弹簧测力计的示数y(单位:N)的变化情况,实验数据记录如下:
x(cm) … 10 15 20 28 …
y(N) … 30 20 15 10 …
其中有一组数据中的x记录错了,x应为 .
11.给某气球充满一定质量的气体,在温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压超过150kPa时,气球会爆炸.由此可判断V=0.04时,气球 爆炸.(用“会”或“不会”填空)
12.如图,菱形ABCO的顶点O是坐标原点,点A在反比例函数的图象上,点B在x轴上.若菱形ABCO的面积是8,则k的值为 .
13.如图,点在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是7,则k的值为 .
14.如图,一次函数y=kx+b与反比例函数的图象相交于点A、点B,与x轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积
(3)根据图象回答:当x为何值时,(请直接写出答案) .
15.中国面食文化至今已有两千多年的历史(面条在东汉称之为“煮饼”).厨师将一定质量的面团做成拉面时,面条的总长度y(m)是面条横截面面积S(mm2)的反比例函数,其图象经过A(4,32),B(a,80)两点(如图).
(1)求y与S之间的函数关系式及a的值;
(2)某厨师拉出的面条最细时的横截面面积不超过0.8mm2,求这根面条的总长度至少有多长.
16.驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得,成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 ;下降阶段的函数解析式为 ;(并写出x的取值范围)
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
17.如图,点A在反比例函数y1=(x>0)的图象上,B、C两点在反比例函数y2=的图象上,BC经过原点,AB⊥x轴,若△ABC的面积为4,则k的值为 .
18.在平面直角坐标系中,直线y=x﹣3与双曲线的图象交于点P(a,b),则代数式的值为 .
19.若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= .
20.已知函数,函数y2=k2x+b(k1,k2,b是常数,且k1k2≠0).
(1)若函数y1和函数y2的图象交于点A(1,m)和点B(3,1).
①求函数y1,y2的解析式;
②若O为平面直角坐标系的原点,直接写出△AOB的面积;
(2)若点C(2,n)在函数y1的图象上,将点C先向下平移2个单位长度,再向左平移4个单位长度得点D,点D恰好落在函数y1的图象上,求n的值.
21.心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
22.在反比例函数y=(x>0)的图象上,有一系列点A1,A2,A3,…,An,An+1,若A1的横坐标为2,以后每个点的横坐标与它前一个点的横坐标的差都为2,过A1,A2,A3,…,An,An+1分别作x轴与y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn= .
23.如图,在平面直角坐标系xOy中,一次函数y1=kx+b的图象与反比例函数的图象交于点A,B,点A的横坐标为2,当x<﹣3时,总有y2>y1恒成立,则k的取值范围是 .
24.如图,已知正比例函数图象经过点A(4,2),B(m,3).
(1)正比例函数的解析式是 ,m的值是 ;
(2)分别过点A与点B作y轴的平行线,与反比例函数在第一象限的分支分别交于点C、D(点C、D均在点A、B下方),若BD:AC=7:3,求反比例函数的解析式;
(3)在第(2)小题的前提下,联结BC,若点E是反比例函数在第一象限的图象上位于点C左侧的一点,且△ABE的面积是△ABC面积的2倍,求点E的坐标.
25.如图,在平面直角坐标系中,点O是坐标原点,一次函数y1=kx+b与反比例函数(x>0)的图象交于A(2,m)、B(4,2)两点.
(1)求一次函数y1与反比例函数y2的解析式;
(2)根据图象回答,当时,x的取值范围为 ;
(3)y轴上有一点P,当以点O、P、A、B为顶点的四边形的面积为7时,求点P的坐标.
26.如图,直线AB与反比例函数的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)连接OA、OB,求△OAB的面积;
(3)是否存在x轴上的一个动点P,使PA+PB最小,若存在求出P点坐标,若不存在,请说明理由.
答案与解析
1.如图,点P在反比例函数图象上,PA⊥x轴于点A,若△POA的面积等于3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
【点拨】根据反比例函数系数k的几何意义即可解决问题.
【解析】解:由题知,
∵PA⊥x轴,△POA的面积等于3,且点P在反比例函数图象上,
∴,
解得k=±6.
又∵k>0,
∴k=6.
故选:C.
【点睛】本题主要考查了反比例函数系数k的几何意义及反比例函数图象上点的坐标特征,熟知反比例函数系数k的几何意义是解题的关键.
2.根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2 C.S小于10m2 D.S大于10m2
【点拨】根据已知条件利用压强公式推导即可得到答案.
【解析】解:∵,F=100,
∴p=,
∵产生的压强P要大于1000Pa,
∴>1000,
∴S<0.1,
故选:A.
【点睛】本题考查了反比例的应用等知识点,熟练掌握其性质是解决此题的关键.
3.如图,函数y1=x﹣1和函数的图象相交于点M(m,1),N(n,﹣2),若y1<y2,则x的取值范围是( )
A.﹣1<x<2 B.x<﹣1或0<x<2 C.﹣1<x<0或0<x<2 D.﹣1<x<0或x>2
【点拨】先求出m、n的值,再根据函数图象即可求解.
【解析】解:∵M(m,1),N(n,﹣2)在函数y1=x﹣1和函数上,
∴m=2,n=﹣1,
即M(2,1),N(﹣1,﹣2),
则y1<y2的范围如图中实线所示:
即x<﹣1或 0<x<2.
故选:B.
【点睛】本题考查的知识点是一次函数与反比例函数图象综合判断,解题关键是结合函数图象解题.
4.某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流I(A)与电阻R(Ω)的关系图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A.当I=0.2时,R=1000 B.I与R的函数表达式是
C.当R>500时,I>0.44 D.当880<R<1000时,则0.22<I<0.25
【点拨】根据题意求出函数表达式,根据函数表达式结合图象即可完成求解.
【解析】解:设反比例函数的解析式为,
把点P坐标代入得:,解得:k=220,
即函数解析式为:,故B不正确;
当I=0.2时,即,解得:R=1100;故A不正确;
当R=500时,,
由图象知,当R>500时,I<0.44;故C不正确;
当R=880时,;当R=1000时,,
表明当880<R<1000时,则0.22<I<0.25;故D正确;
故选:D.
【点睛】本题考查了反比例函数的应用,正确求出反比例函数解析式是解题的关键.
5.如图,点B,C分别是反比例函数与的图象上的点,且BC∥y轴,过点C作BC的垂线交y轴于点A,则△ABC的面积为( )
A.6 B.4 C.3 D.2
【点拨】过点B作BD⊥y轴于点D,记BC交x轴于点E,利用反比例函数比例系数k的几何意义求出矩形ACBD的面积,利用矩形的性质求出△ABC的面积.
【解析】解:过点B作BD⊥y轴于点D,记BC交x轴于点E,
∵BC∥y轴,AC⊥BC,
∴S矩形AOEC=|﹣2|=2,S矩形DOEB=|6|=6,
∴S矩形ACBD=S矩形AOEC+S矩形DOEB=2+6=8,
∴S△ABC=S矩形ACBD=4.
故选:B.
【点睛】本题考查了反比例函数比例系数k的几何意义,即过双曲线上任意一点引x轴、y轴的垂线,所得矩形面积为|k|,解题的关键是过点B作BD⊥y轴于点D构造矩形.
6.如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
A.S1=S2+S3 B.S2=S3 C.S3>S2>S1 D.S1S2<S2S3
【点拨】根据反比例函数系数k的几何意义即可得到结论.
【解析】解:根据条件可得:,,
∴S△AOD>S△BOE﹣S△OME=S△COF﹣S△OME,
∴S1>S2=S3.
故答案为:B.
【点睛】本题考查了反比例函数的k值几何意义、反比例函数图象上点的坐标特征,掌握反比例函数的性质是解题的关键.
7.反比例函数与直线y=k2x+b的图象在坐标轴中位置如图所示,下列结论中错误的是( )
A.直线y=k2x+b与坐标轴围成的三角形的面积是2
B.反比例函数与直线y=k2x+b的图象的交点坐标为(﹣1,﹣3),(3,1)
C.b<0<k2<k1
D.当﹣1<x<3时,有
【点拨】根据题意,分别求出反比例函数及一次函数的解析式,再对所给选项依次进行判断即可.
【解析】解:由题知,
将点(3,1)代入y=得,
k1=3×1=3,
所以反比例函数解析式为y=.
将点(3,1)和(﹣1,﹣3)代入y=k2x+b得,
,
解得,
所以一次函数的解析式为y=x﹣2,
则一次函数与坐标轴的交点坐标分别为(2,0),(0,﹣2),
所以直线y=k2x+b与坐标轴围成的三角形的面积是:.
故A选项不符合题意.
由函数图象可知,
反比例函数与直线y=k2x+b的图象的交点坐标为(﹣1,﹣3),(3,1).
故B选项不符合题意.
因为﹣2<0<1<3,
所以b<0<k2<k1.
故C选项不符合题意.
由函数图象可知,
当﹣1<x<0或x>3时,一次函数的图象在反比例函数图象的上方,即,
所以当﹣1<x<0或x>3时,有.
故D选项符合题意.
故选:D.
【点睛】本题主要考查了反比例函数与一次函数的交点问题,熟知反比例函数及一次函数的图象与性质是解题的关键.
8.已知反比例函数与正比例函数y=2x图象的一个交点坐标为(2,4),则另一个交点坐标为 (﹣2,﹣4) .
【点拨】反比例函数的图象是中心对称图形,与经过原点的直线的两个交点一定关于原点对称.
【解析】解:∵反比例函数的图象与正比例函数的图象的一个交点坐标为(2,4),
∴另一个交点的坐标是(﹣2,﹣4).
故答案为:(﹣2,﹣4).
【点睛】本题考查正比例和反比例函数图象的中心对称性,根据已知得出反比例函数与经过原点的直线的两个交点一定关于原点对称是解题关键.
9.一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=20m3时,ρ=1.36kg/m3,当V=40m3时,ρ= 0.68 kg/m3.
【点拨】根据题意可知一定质量的氧气,它的密度ρ是它的体积V的反比例函数,且已知当V=20m3时,ρ=1.36kg/m3,故p与V的函数关系式是ρ=,把V=40m3代入解析式求解即可求得ρ的值.
【解析】解:设ρ与V的函数关系式为ρ=,
当V=20m3时,ρ=1.36kg/m3,
∴1.36=,
∴k=1.36×20=27.2,
∴ρ与V的函数关系式是ρ=;
当V=40m3时,ρ==0.68(kg/m3).
故答案为:0.68.
【点睛】本题考查了反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
10.如图,小华设计了一个探索杠杆平衡条件的实验,在一根匀质的木杆中点O处用一根细绳挂在支架上,在点O的左侧固定位置B处悬挂重物A,在点O的右侧用一个弹簧测力计向下拉木杆,使木杆达到平衡(杠杆平衡时,动力×动力臂=阻力×阻力臂).改变弹簧测力计与点O的距离x(单位:cm),观察弹簧测力计的示数y(单位:N)的变化情况,实验数据记录如下:
x(cm) … 10 15 20 28 …
y(N) … 30 20 15 10 …
其中有一组数据中的x记录错了,x应为 30 .
【点拨】先由表格数据求出y与x的函数关系,再找出其中错误的一组即可.
【解析】解:y与x成反比例函数关系,设,
由条件可知k=300,
∴,
当y=10时,x=30,
故其中有一组数据记录错了,这组数据对应的x是30.
故答案为:30.
【点睛】本题考查反比例函数的实际应用.理解题意,列出反比例函数解析式是关键.
11.给某气球充满一定质量的气体,在温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压超过150kPa时,气球会爆炸.由此可判断V=0.04时,气球 不会 爆炸.(用“会”或“不会”填空)
【点拨】设P=,将A(2,2.4)代入求出k=4.8,求得P=,由P>150KPa时,气球将爆炸,得到P≤150,即P=≤150,求得V≥=0.032(m3).因为0.032<0.04,于是得到气球不会爆炸.
【解析】解:设P=,将A(2,2.4)代入求出k=4.8,
∴P=,
当P>150KPa时,气球将爆炸,
∴P≤150,即P=≤150,
解得V≥=0.032(m3).
∵0.032<0.04,
∴气球不会爆炸,
故答案为:不会.
【点睛】本题考查了反比例函数的实际应用,关键是建立函数关系式,并会运用函数关系式解答题目的问题.
12.如图,菱形ABCO的顶点O是坐标原点,点A在反比例函数的图象上,点B在x轴上.若菱形ABCO的面积是8,则k的值为 ﹣4 .
【点拨】根据反比例函数k值几何意义解答即可.
【解析】解:如图,作AD⊥x轴,垂足为D,
∵S菱形ABCO=8,
∴S△ABO=4,
∵AB=AO,AD⊥BO,
∴S△AOD=2,
∴|k|=2S△AOD=4,
∵反比例函数图象在第二象限,
∴k=﹣4.
故答案为:﹣4.
【点睛】本题考查了反比例函数k值的几何意义,熟练掌握该知识点是关键.
13.如图,点在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是7,则k的值为 12 .
【点拨】先根据反比例函数的图象在第一象限判断出k的符号,再延长线段BA,交y轴于点E,由于AB∥x轴,所以AE⊥y轴,故四边形AEOD是矩形,由于点A在双曲线y=上,所以S矩形AEOD=5,同理可得S矩形OCBE=k,由S矩形ABCD=S矩形OCBE﹣S矩形AEOD即可得出k的值.
【解析】解:∵双曲线y=(k≠0)在第一象限,
∴k>0,
延长线段BA,交y轴于点E,
∵AB∥x轴
∴AE⊥y轴,
∴四边形AEOD是矩形,
∵点在双曲线y=上,
∴S矩形AEOD=5,
同理S矩形OCBE=k,
∵S矩形ABCD=S矩形OCBE﹣S矩形AEOD=k﹣5=7,
∴k=12.
故答案为12.
【点睛】本题考查的是反比例函数系数k的几何意义,即在反比例函数y=图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
14.如图,一次函数y=kx+b与反比例函数的图象相交于点A、点B,与x轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ﹣3 ,n= 1 .
(2)求一次函数的解析式和△AOB的面积
(3)根据图象回答:当x为何值时,(请直接写出答案) ﹣3<x<﹣1 .
【点拨】(1)将A点坐标,B点坐标代入解析式可求m,n的值
(2)用待定系数法可求一次函数解析式,根据S△AOB=S△AOC﹣S△BOC可求△AOB的面积.
(3)由图象直接可得.
【解析】解:(1)∵反比例函数的图象过点A(﹣1,3),B(﹣3,n)
∴m=3×(﹣1)=﹣3,m=﹣3n
∴n=1
故答案为﹣3,1
(2)设一次函数解析式y=kx+b,且过(﹣1,3),B(﹣3,1)
∴解得:
∴一次函数的解析式为y=x+4
∵一次函数图象与x轴交点为C
∴0=x+4
∴x=﹣4
∴C(﹣4,0)
∵S△AOB=S△AOC﹣S△BOC
∴S△AOB=×4×3﹣×4×1=4
(3)∵,即kx+b>,
∴一次函数图象在反比例函数图象上方,
∴﹣3<x<﹣1
故答案为﹣3<x<﹣1.
【点睛】本题考查了反比例函数与一次函数的交点问题,待定系数法,利用函数图象上的点满足函数关系式解决问题是本题关键.
15.中国面食文化至今已有两千多年的历史(面条在东汉称之为“煮饼”).厨师将一定质量的面团做成拉面时,面条的总长度y(m)是面条横截面面积S(mm2)的反比例函数,其图象经过A(4,32),B(a,80)两点(如图).
(1)求y与S之间的函数关系式及a的值;
(2)某厨师拉出的面条最细时的横截面面积不超过0.8mm2,求这根面条的总长度至少有多长.
【点拨】(1)设y与x之间的函数表达式为:,将(4,32)代入可得解析式,再把将(a,80)代入解析式可得a的值;
(2)厨师做出的面条横截面面积不超过0.8mm2,可得列式得,解不等式即可.
【解析】解:(1)设y与x之间的函数表达式为:,
由条件可得:k=128,
∴y与S之间的函数表达式为:;
将(a,80)代入可得a=1.6;
(2)由条件可知,
故面条的总长度至少为160m.
【点睛】本题主要考查反比例函数的运用,求不等式的解集,掌握待定系数法求解析式,反比例函数图象的性质,求不等式的解集是解题的关键.
16.驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得,成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 y=100x(0≤x≤4) ;下降阶段的函数解析式为 y=(4≤x≤10) ;(并写出x的取值范围)
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
【点拨】(1)当0≤x≤4时,设直线解析式为:y=kx,当4≤x≤10时,设反比例函数解析式为:y=,利用待定系数法即可解决问题;
(2)分别求出y=200时的两个函数值,再求时间差即可解决问题.
【解析】解:(1)当0≤x≤4时,设直线解析式为:y=kx,将(4,400)代入得:400=4k,
解得:k=100,故直线解析式为:y=100x,
当4≤x≤10时,设反比例函数解析式为:y=,将(4,400)代入得:400=,
解得:a=1600,故反比例函数解析式为:y=;
因此血液中药物浓度上升阶段的函数关系式为y=100x(0≤x≤4),
下降阶段的函数关系式为y=(4≤x≤10).
故答案为:y=100x(0≤x≤4),y=(4≤x≤10);
(2)当y=200,则200=100x,
解得:x=2,
当y=200,则200=,
解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于200微克/毫升的持续时间6小时.
【点睛】本题考查一次函数的应用、反比例函数的应用等知识,解题的关键是灵活应用待定系数法解决问题,学会利用函数图象解决实际问题,属于中考常考题型.
17.如图,点A在反比例函数y1=(x>0)的图象上,B、C两点在反比例函数y2=的图象上,BC经过原点,AB⊥x轴,若△ABC的面积为4,则k的值为 ﹣3 .
【点拨】设A(a,),B(a,),根据BC经过原点,且B、C两点在反比例函数y2=的图象上,得到点B和点C关于原点对称,求得C(﹣a,﹣),根据三角形的面积公式列方程即可得到结论.
【解析】解:设A(a,),
∵AB⊥x轴,
∴B(a,),
∵BC经过原点,且B、C两点在反比例函数y2=的图象上,
∴点B和点C关于原点对称,
∴C(﹣a,﹣),
∵AB=﹣=,△ABC的面积为4,
∴××2a=4,
∴k=﹣3,
故答案为:﹣3,
解法二:连接OA,设AB于x轴交于M,
∵BC经过原点,
∴C,B关于原点对称,
∴OB=OC,
∵△ABC的面积为4,
∴S△AOB=S△ABC=2,
∵点A在反比例函数y1=(x>0)的图象上,
∴OM AM=1,
∴S△BOM=S△AOB﹣S△AOM=2﹣OM AB=,
∴OM BM=2S△BMO=3,
即|k|=3,
∵k<0,
∴k=﹣3.
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数的性质,三角形的面积的计算,熟练掌握反比例函数的性质是解题的关键.
18.在平面直角坐标系中,直线y=x﹣3与双曲线的图象交于点P(a,b),则代数式的值为 ﹣ .
【点拨】由题意得ab=21,b=a﹣3,即可求解.
【解析】解:∵函数y=(x>0)与y=x﹣3的图象交于点P(a,b),
∴ab=21,b=a﹣3,
∴b﹣a=﹣3,
∴==﹣,
故答案为:﹣.
【点睛】此题主要考查了一次函数图象上点的坐标特征以及反比例函数图象上点的特征,正确得出a、b之间的关系是解题关键.
19.若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= ﹣4 .
【点拨】由直线y=﹣2x与反比例函数的图象都关于原点对称,可得(x1,y1),(x2,y2)两点也关于原点对称,则有x2=﹣x1,y2=﹣y1,再代入(y2﹣y1)(x1﹣x2)=16整理得x1y1=﹣4,再利用反比例函数的解析式即可求解.
【解析】解:∵直线y=﹣2x的图象与反比例函数的图象都关于原点对称,且交于(x1,y1),(x2,y2)两点,
∴x2=﹣x1,y2=﹣y1,
由条件可知(﹣y1﹣y1)(x1+x1)=16,
整理得:x1y1=﹣4,
∵(x1,y1)在反比例函数的图象上,
∴k=x1y1=﹣4.
故答案为:﹣4.
【点睛】本题考查了一次函数与反比例函数的交点问题,熟练掌握一次函数与反比例函数的图象与性质是解题的关键.
20.已知函数,函数y2=k2x+b(k1,k2,b是常数,且k1k2≠0).
(1)若函数y1和函数y2的图象交于点A(1,m)和点B(3,1).
①求函数y1,y2的解析式;
②若O为平面直角坐标系的原点,直接写出△AOB的面积;
(2)若点C(2,n)在函数y1的图象上,将点C先向下平移2个单位长度,再向左平移4个单位长度得点D,点D恰好落在函数y1的图象上,求n的值.
【点拨】(1)①利用待定系数法求函数解析式;
②利用函数图象,结合反比例函数的几何意义,可得S△AOB=S梯形ACDB=(AC+BD)×CD=(3+1)×2=4,进而可以得解;
(2)根据平移确定点D的坐标,然后利用函数图象上点的坐标特征代入求解.
【解析】解:(1)①由题意,把点B(3,1)代入,
∴.
∴k1=3.
∴函数y1的表达式为.
把点A(1,m)代入,
∴m=3.
把点A(1,3),点B(3,1)代入y2=k2x+b,
∴.
∴.
∴函数y2的表达式为y2=﹣x+4.
②如图,由(1)得,A(1,3),点B(3,1),
∴AC=3,BD=1,CD=2.
由题意,根据反比例函数的几何意义可得,S△AOB=S梯形ACDB=(AC+BD)×CD=(3+1)×2=4.
(2)由平移,∵C(2,n)在函数y1的图象上,
∴D(﹣2,n﹣2).
∴﹣2(n﹣2)=2n.
∴n=1.
【点睛】本题主要考查了反比例函数与一次函数的交点问题,解题时要熟练掌握并能灵活运用反比例函数的几何意义进行分析是关键.
21.心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
【点拨】(1)从图象上看,AB表示的函数为一次函数,BC是平行于x轴的线段,CD为双曲线的一部分,设出解析式,代入数值可以解答,把自变量的值代入相对应的函数解析式,求出对应的函数值比较得出;
(2)求出相对应的自变量的值,代入相对应的函数解析式,求出注意力指标数与40相比较,得出答案.
【解析】解:(1)设yAB=k1x+b,把(0,20),(10,50)代入函数解析式解得yAB=3x+20(0≤x≤10),
由图象直接得到yBC=50(10≤x≤30),
设yCD=,把(30,50)代入函数解析式解得yCD=(30≤x≤45);
把x=5代入yAB=3x+20,得yAB=35,
把x=35代入yCD=,得yCD=,
因为yAB≤yCD,
所以第35分钟时学生的注意力更集中;
(2)由题意知,注意力指数不低于40
即当在3x+20≥40,x≥
同时≥40
即x≤=37.5
即当开始上课分钟直至上课37.5分钟时学生的注意力指数均不小于40.
而37.5﹣>30,
∴该学习设计合理.
【点睛】此题主要考查了反比例函数的应用,此题属于分段函数,根据实际情况,结合图象,求出相对应的函数解析式,计算出数值,代入相应的函数解析式解决问题.
22.在反比例函数y=(x>0)的图象上,有一系列点A1,A2,A3,…,An,An+1,若A1的横坐标为2,以后每个点的横坐标与它前一个点的横坐标的差都为2,过A1,A2,A3,…,An,An+1分别作x轴与y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn= .
【点拨】由已知条件横坐标成等差数列,再根据点A1、A2、A3、…、An、An+1在反比例函数上,求出各点坐标,即可求出S1,S2,S3,进而求出S1+S2+S3+…+Sn,即可作答.
【解析】解:∵点A1、A2、A3、…、An、An+1都在反比例函数的图象上,且A1的横坐标为2,
则,
∴A1(2,6),
由条件可知,
∴A2(4,3)、
则,
∴A3(6,2),
依次类推得,
∴S1=2×(6﹣3),
S2=2×(3﹣2),
,
……,
,
∴S1+S2+S3+…+Sn
=
=
=.
故答案为:.
【点睛】本题主要考查了反比例函数的性质,坐标规律探索,发现规律是关键.
23.如图,在平面直角坐标系xOy中,一次函数y1=kx+b的图象与反比例函数的图象交于点A,B,点A的横坐标为2,当x<﹣3时,总有y2>y1恒成立,则k的取值范围是 k≥1 .
【点拨】首先确定点A的坐标(2,3),由一次函数y=kx+b经过点A,推出3=2k+b,推出b=3﹣2k,推出一次函数的解析式为y=kx+3﹣2k,再构建不等式求解.
【解析】解:∵点A在y=的图象上,横坐标是2,
∴A(2,3),
∵一次函数y=kx+b经过点A,
∴3=2k+b,
∴b=3﹣2k,
∴一次函数的解析式为y=kx+3﹣2k,
由题意当x<﹣3时,总有y2>y1恒成立,
∴﹣2≥﹣3k+3﹣2k,
∴k≥1.
故答案为:k≥1.
【点睛】本题考查反比例函数与一次函数的交点,解题的关键是理解题意,灵活运用所学知识解决问题.
24.如图,已知正比例函数图象经过点A(4,2),B(m,3).
(1)正比例函数的解析式是 ,m的值是 6 ;
(2)分别过点A与点B作y轴的平行线,与反比例函数在第一象限的分支分别交于点C、D(点C、D均在点A、B下方),若BD:AC=7:3,求反比例函数的解析式;
(3)在第(2)小题的前提下,联结BC,若点E是反比例函数在第一象限的图象上位于点C左侧的一点,且△ABE的面积是△ABC面积的2倍,求点E的坐标.
【点拨】(1)用待定系数法即可求解;
(1)BD:AC=7:3,即(6﹣):(4﹣)=7:3,即可求解;
(3)过点C作AB的平行线CN交y轴于点N,如图,取OM=2ON,过点M作ME∥AB交反比例函数于点E,即可求解.
【解析】解:(1)设正比例函数的表达式为:y=tx,
将点A、B的坐标代入上式得:2=4t,3=mt,
解得:t=,m=6,
故答案为:,6;
(1)由(1)知,正比例函数的表达式为:y=x,点B(3,6),
设反比例函数的解析式的表达式为:y=,
设点C(4,),B(6,),
∵BD:AC=7:3,即(6﹣):(4﹣)=7:3,
解得:k=4,
则反比例函数的表达式为:y=;
(3)过点C作AB的平行线CN交y轴于点N,如图,取OM=2ON,过点M作ME∥AB交反比例函数于点E,
则此时,△ABE的面积是△ABC面积的2倍,
∵CN∥AB∥ME,
故直线CN的表达式为:y=(x﹣4)+1,则点N(0,﹣1),即ON=1,则OM=2,
即点M(0,2),则直线ME的表达式为:y=x+2,
联立上式和反比例函数的表达式得:=x+2,
解得:x=﹣2+2(负值已舍去),
即点E(﹣2+2,).
【点睛】本题为反比例函数综合运用,涉及到平行线的性质,面积的计算、求函数表达式等,利用平行线的性质确定面积之间的关系是解题的关键.
25.如图,在平面直角坐标系中,点O是坐标原点,一次函数y1=kx+b与反比例函数(x>0)的图象交于A(2,m)、B(4,2)两点.
(1)求一次函数y1与反比例函数y2的解析式;
(2)根据图象回答,当时,x的取值范围为 0<x≤2或x≥4 ;
(3)y轴上有一点P,当以点O、P、A、B为顶点的四边形的面积为7时,求点P的坐标.
【点拨】(1)把B(4,2)代得2=,解方程得到反比例函数y2的解析式为y2=,把A(2,m)代入y2=得,m==4,求得A(2,4),把A(2,4),B(4,2)代入y1=kx+b得解方程组得到一次函数y1的解析式为y1=﹣x+6;
(2)根据函数图象即可得到不等式的解集;
(3)设P(0,a),解方程得到M(0,6),N(6,0),根据三角形的面积公式即可得到结论.
【解析】解:(1)把B(4,2)代得2=,
∴n=8,
∴反比例函数y2的解析式为y2=,
把A(2,m)代入y2=得,m==4,
∴A(2,4),
把A(2,4),B(4,2)代入y1=kx+b得,,
∴,
∴一次函数y1的解析式为y1=﹣x+6;
(2)由图象得,当时,x的取值范围为0<x≤2或x≥4;
故答案为:0<x≤2或x≥4;
(3)设P(0,a),
在y1=﹣x+6中,当x=0时,y=6,当y=0时,x=6,
∴M(0,6),N(6,0),
∴S四边形ABOP=S△MON﹣S△APM﹣S△OBN=﹣×(6﹣a)×2﹣×6×2=7或S四边形AOPB=S△MON﹣S△AOM﹣S△OBN+S△OBP=﹣×6×2﹣×6×2+×(﹣a)×4=7
∴a=1或﹣0.5,
∴点P的坐标为(0,1)或(0,﹣0.5).
【点睛】本题是反比例函数综合题,考查了待定系数法求函数的解析式,三角形的面积,正确地求出函数的解析式是解题的关键.
26.如图,直线AB与反比例函数的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)连接OA、OB,求△OAB的面积;
(3)是否存在x轴上的一个动点P,使PA+PB最小,若存在求出P点坐标,若不存在,请说明理由.
【点拨】(1)把A(1,4)代入y= 中,求出m的值,即可得反比例函数解析式为y=;
(2)分别过点A、B作AC⊥x轴,交x轴于点C、交OB于点E,过点B作BD⊥x轴,交x轴于点D.先求出B点的坐标为B(4,1).由反比例函数的几何意义可得S△OAC=S△OBD==2,则可得S△OAE=S梯形CEBD,进而可得S△OAB=S梯形ACDB,根据梯形的面积公式即可求解;
(3)作点A关于x轴的对称点A′,连接A′B交x轴于P,此时PA+PB的值最小.求出A′B的表达式为y=x﹣,再求出y=0时x的值,即可得P点的坐标.
【解析】解:(1)把A(1,4)代入y=得m=1×4=4,
∴反比例函数解析式为y=;
(2)分别过点A、B作AC⊥x轴,交x轴于点C、交OB于点E,过点B作BD⊥x轴,交x轴于点D,如图1,
由(1)可知,反比例函数解析式为y=,
把B(4,n)代入y=,得4n=4,
解得n=1,
∴B(4,1).
∵S△OAC=S△OCE+S△OAE==2,S△OBD=S△OCE+S梯形CEBD==2,
∴S△OAE=S梯形CEBD,
∵S△OAB=S△OAE+S△ABE,
∴S△OAB=S梯形CEBD+S△ABE=S梯形ACDB,
∴S△OAB=(|yA|+|yB|)(xB﹣xA)=×(4+1)×(4﹣1)=;
(3)存在x轴上的一个动点P,使PA+PB最小;理由如下:
作点A关于x轴的对称点A′,如图,则A′(1,﹣4),连接A′B交x轴于P,则PA=PA′,
∴PA+PB=PA′+PB=A′B,
∴此时PA+PB的值最小,
设直线A′B的解析式为y=kx+b,
把A′(1,﹣4),B(4,1)代入得:
,
解得,
∴直线A′B的解析式为y=x﹣,
当y=0时,x﹣=0,
解得x=,
∴P点坐标为(,0).
【点睛】本题属于反比例函数综合题,主要考查了用待定系数法求反比例函数的表达式、反以及反比例函数的几何意义以及利用将军饮马求点的坐标.熟练掌握反比例函数k的几何意义是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
6.3 反比例函数的应用 同步分层作业
1.如图,点P在反比例函数图象上,PA⊥x轴于点A,若△POA的面积等于3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
2.根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2 C.S小于10m2 D.S大于10m2
3.如图,函数y1=x﹣1和函数的图象相交于点M(m,1),N(n,﹣2),若y1<y2,则x的取值范围是( )
A.﹣1<x<2 B.x<﹣1或0<x<2 C.﹣1<x<0或0<x<2 D.﹣1<x<0或x>2
4.某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流I(A)与电阻R(Ω)的关系图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A.当I=0.2时,R=1000 B.I与R的函数表达式是
C.当R>500时,I>0.44 D.当880<R<1000时,则0.22<I<0.25
5.如图,点B,C分别是反比例函数与的图象上的点,且BC∥y轴,过点C作BC的垂线交y轴于点A,则△ABC的面积为( )
A.6 B.4 C.3 D.2
6.如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
A.S1=S2+S3 B.S2=S3 C.S3>S2>S1 D.S1S2<S2S3
7.反比例函数与直线y=k2x+b的图象在坐标轴中位置如图所示,下列结论中错误的是( )
A.直线y=k2x+b与坐标轴围成的三角形的面积是2
B.反比例函数与直线y=k2x+b的图象的交点坐标为(﹣1,﹣3),(3,1)
C.b<0<k2<k1
D.当﹣1<x<3时,有
8.已知反比例函数与正比例函数y=2x图象的一个交点坐标为(2,4),则另一个交点坐标为 .
9.一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=20m3时,ρ=1.36kg/m3,当V=40m3时,ρ= kg/m3.
10.如图,小华设计了一个探索杠杆平衡条件的实验,在一根匀质的木杆中点O处用一根细绳挂在支架上,在点O的左侧固定位置B处悬挂重物A,在点O的右侧用一个弹簧测力计向下拉木杆,使木杆达到平衡(杠杆平衡时,动力×动力臂=阻力×阻力臂).改变弹簧测力计与点O的距离x(单位:cm),观察弹簧测力计的示数y(单位:N)的变化情况,实验数据记录如下:
x(cm) … 10 15 20 28 …
y(N) … 30 20 15 10 …
其中有一组数据中的x记录错了,x应为 .
11.给某气球充满一定质量的气体,在温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压超过150kPa时,气球会爆炸.由此可判断V=0.04时,气球 爆炸.(用“会”或“不会”填空)
12.如图,菱形ABCO的顶点O是坐标原点,点A在反比例函数的图象上,点B在x轴上.若菱形ABCO的面积是8,则k的值为 .
13.如图,点在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是7,则k的值为 .
14.如图,一次函数y=kx+b与反比例函数的图象相交于点A、点B,与x轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积
(3)根据图象回答:当x为何值时,(请直接写出答案) .
15.中国面食文化至今已有两千多年的历史(面条在东汉称之为“煮饼”).厨师将一定质量的面团做成拉面时,面条的总长度y(m)是面条横截面面积S(mm2)的反比例函数,其图象经过A(4,32),B(a,80)两点(如图).
(1)求y与S之间的函数关系式及a的值;
(2)某厨师拉出的面条最细时的横截面面积不超过0.8mm2,求这根面条的总长度至少有多长.
16.驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得,成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 ;下降阶段的函数解析式为 ;(并写出x的取值范围)
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
17.如图,点A在反比例函数y1=(x>0)的图象上,B、C两点在反比例函数y2=的图象上,BC经过原点,AB⊥x轴,若△ABC的面积为4,则k的值为 .
18.在平面直角坐标系中,直线y=x﹣3与双曲线的图象交于点P(a,b),则代数式的值为 .
19.若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= .
20.已知函数,函数y2=k2x+b(k1,k2,b是常数,且k1k2≠0).
(1)若函数y1和函数y2的图象交于点A(1,m)和点B(3,1).
①求函数y1,y2的解析式;
②若O为平面直角坐标系的原点,直接写出△AOB的面积;
(2)若点C(2,n)在函数y1的图象上,将点C先向下平移2个单位长度,再向左平移4个单位长度得点D,点D恰好落在函数y1的图象上,求n的值.
21.心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
22.在反比例函数y=(x>0)的图象上,有一系列点A1,A2,A3,…,An,An+1,若A1的横坐标为2,以后每个点的横坐标与它前一个点的横坐标的差都为2,过A1,A2,A3,…,An,An+1分别作x轴与y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn= .
23.如图,在平面直角坐标系xOy中,一次函数y1=kx+b的图象与反比例函数的图象交于点A,B,点A的横坐标为2,当x<﹣3时,总有y2>y1恒成立,则k的取值范围是 .
24.如图,已知正比例函数图象经过点A(4,2),B(m,3).
(1)正比例函数的解析式是 ,m的值是 ;
(2)分别过点A与点B作y轴的平行线,与反比例函数在第一象限的分支分别交于点C、D(点C、D均在点A、B下方),若BD:AC=7:3,求反比例函数的解析式;
(3)在第(2)小题的前提下,联结BC,若点E是反比例函数在第一象限的图象上位于点C左侧的一点,且△ABE的面积是△ABC面积的2倍,求点E的坐标.
25.如图,在平面直角坐标系中,点O是坐标原点,一次函数y1=kx+b与反比例函数(x>0)的图象交于A(2,m)、B(4,2)两点.
(1)求一次函数y1与反比例函数y2的解析式;
(2)根据图象回答,当时,x的取值范围为 ;
(3)y轴上有一点P,当以点O、P、A、B为顶点的四边形的面积为7时,求点P的坐标.
26.如图,直线AB与反比例函数的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)连接OA、OB,求△OAB的面积;
(3)是否存在x轴上的一个动点P,使PA+PB最小,若存在求出P点坐标,若不存在,请说明理由.
答案与解析
1.如图,点P在反比例函数图象上,PA⊥x轴于点A,若△POA的面积等于3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
【点拨】根据反比例函数系数k的几何意义即可解决问题.
【解析】解:由题知,
∵PA⊥x轴,△POA的面积等于3,且点P在反比例函数图象上,
∴,
解得k=±6.
又∵k>0,
∴k=6.
故选:C.
【点睛】本题主要考查了反比例函数系数k的几何意义及反比例函数图象上点的坐标特征,熟知反比例函数系数k的几何意义是解题的关键.
2.根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2 C.S小于10m2 D.S大于10m2
【点拨】根据已知条件利用压强公式推导即可得到答案.
【解析】解:∵,F=100,
∴p=,
∵产生的压强P要大于1000Pa,
∴>1000,
∴S<0.1,
故选:A.
【点睛】本题考查了反比例的应用等知识点,熟练掌握其性质是解决此题的关键.
3.如图,函数y1=x﹣1和函数的图象相交于点M(m,1),N(n,﹣2),若y1<y2,则x的取值范围是( )
A.﹣1<x<2 B.x<﹣1或0<x<2 C.﹣1<x<0或0<x<2 D.﹣1<x<0或x>2
【点拨】先求出m、n的值,再根据函数图象即可求解.
【解析】解:∵M(m,1),N(n,﹣2)在函数y1=x﹣1和函数上,
∴m=2,n=﹣1,
即M(2,1),N(﹣1,﹣2),
则y1<y2的范围如图中实线所示:
即x<﹣1或 0<x<2.
故选:B.
【点睛】本题考查的知识点是一次函数与反比例函数图象综合判断,解题关键是结合函数图象解题.
4.某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流I(A)与电阻R(Ω)的关系图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A.当I=0.2时,R=1000 B.I与R的函数表达式是
C.当R>500时,I>0.44 D.当880<R<1000时,则0.22<I<0.25
【点拨】根据题意求出函数表达式,根据函数表达式结合图象即可完成求解.
【解析】解:设反比例函数的解析式为,
把点P坐标代入得:,解得:k=220,
即函数解析式为:,故B不正确;
当I=0.2时,即,解得:R=1100;故A不正确;
当R=500时,,
由图象知,当R>500时,I<0.44;故C不正确;
当R=880时,;当R=1000时,,
表明当880<R<1000时,则0.22<I<0.25;故D正确;
故选:D.
【点睛】本题考查了反比例函数的应用,正确求出反比例函数解析式是解题的关键.
5.如图,点B,C分别是反比例函数与的图象上的点,且BC∥y轴,过点C作BC的垂线交y轴于点A,则△ABC的面积为( )
A.6 B.4 C.3 D.2
【点拨】过点B作BD⊥y轴于点D,记BC交x轴于点E,利用反比例函数比例系数k的几何意义求出矩形ACBD的面积,利用矩形的性质求出△ABC的面积.
【解析】解:过点B作BD⊥y轴于点D,记BC交x轴于点E,
∵BC∥y轴,AC⊥BC,
∴S矩形AOEC=|﹣2|=2,S矩形DOEB=|6|=6,
∴S矩形ACBD=S矩形AOEC+S矩形DOEB=2+6=8,
∴S△ABC=S矩形ACBD=4.
故选:B.
【点睛】本题考查了反比例函数比例系数k的几何意义,即过双曲线上任意一点引x轴、y轴的垂线,所得矩形面积为|k|,解题的关键是过点B作BD⊥y轴于点D构造矩形.
6.如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
A.S1=S2+S3 B.S2=S3 C.S3>S2>S1 D.S1S2<S2S3
【点拨】根据反比例函数系数k的几何意义即可得到结论.
【解析】解:根据条件可得:,,
∴S△AOD>S△BOE﹣S△OME=S△COF﹣S△OME,
∴S1>S2=S3.
故答案为:B.
【点睛】本题考查了反比例函数的k值几何意义、反比例函数图象上点的坐标特征,掌握反比例函数的性质是解题的关键.
7.反比例函数与直线y=k2x+b的图象在坐标轴中位置如图所示,下列结论中错误的是( )
A.直线y=k2x+b与坐标轴围成的三角形的面积是2
B.反比例函数与直线y=k2x+b的图象的交点坐标为(﹣1,﹣3),(3,1)
C.b<0<k2<k1
D.当﹣1<x<3时,有
【点拨】根据题意,分别求出反比例函数及一次函数的解析式,再对所给选项依次进行判断即可.
【解析】解:由题知,
将点(3,1)代入y=得,
k1=3×1=3,
所以反比例函数解析式为y=.
将点(3,1)和(﹣1,﹣3)代入y=k2x+b得,
,
解得,
所以一次函数的解析式为y=x﹣2,
则一次函数与坐标轴的交点坐标分别为(2,0),(0,﹣2),
所以直线y=k2x+b与坐标轴围成的三角形的面积是:.
故A选项不符合题意.
由函数图象可知,
反比例函数与直线y=k2x+b的图象的交点坐标为(﹣1,﹣3),(3,1).
故B选项不符合题意.
因为﹣2<0<1<3,
所以b<0<k2<k1.
故C选项不符合题意.
由函数图象可知,
当﹣1<x<0或x>3时,一次函数的图象在反比例函数图象的上方,即,
所以当﹣1<x<0或x>3时,有.
故D选项符合题意.
故选:D.
【点睛】本题主要考查了反比例函数与一次函数的交点问题,熟知反比例函数及一次函数的图象与性质是解题的关键.
8.已知反比例函数与正比例函数y=2x图象的一个交点坐标为(2,4),则另一个交点坐标为 (﹣2,﹣4) .
【点拨】反比例函数的图象是中心对称图形,与经过原点的直线的两个交点一定关于原点对称.
【解析】解:∵反比例函数的图象与正比例函数的图象的一个交点坐标为(2,4),
∴另一个交点的坐标是(﹣2,﹣4).
故答案为:(﹣2,﹣4).
【点睛】本题考查正比例和反比例函数图象的中心对称性,根据已知得出反比例函数与经过原点的直线的两个交点一定关于原点对称是解题关键.
9.一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=20m3时,ρ=1.36kg/m3,当V=40m3时,ρ= 0.68 kg/m3.
【点拨】根据题意可知一定质量的氧气,它的密度ρ是它的体积V的反比例函数,且已知当V=20m3时,ρ=1.36kg/m3,故p与V的函数关系式是ρ=,把V=40m3代入解析式求解即可求得ρ的值.
【解析】解:设ρ与V的函数关系式为ρ=,
当V=20m3时,ρ=1.36kg/m3,
∴1.36=,
∴k=1.36×20=27.2,
∴ρ与V的函数关系式是ρ=;
当V=40m3时,ρ==0.68(kg/m3).
故答案为:0.68.
【点睛】本题考查了反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
10.如图,小华设计了一个探索杠杆平衡条件的实验,在一根匀质的木杆中点O处用一根细绳挂在支架上,在点O的左侧固定位置B处悬挂重物A,在点O的右侧用一个弹簧测力计向下拉木杆,使木杆达到平衡(杠杆平衡时,动力×动力臂=阻力×阻力臂).改变弹簧测力计与点O的距离x(单位:cm),观察弹簧测力计的示数y(单位:N)的变化情况,实验数据记录如下:
x(cm) … 10 15 20 28 …
y(N) … 30 20 15 10 …
其中有一组数据中的x记录错了,x应为 30 .
【点拨】先由表格数据求出y与x的函数关系,再找出其中错误的一组即可.
【解析】解:y与x成反比例函数关系,设,
由条件可知k=300,
∴,
当y=10时,x=30,
故其中有一组数据记录错了,这组数据对应的x是30.
故答案为:30.
【点睛】本题考查反比例函数的实际应用.理解题意,列出反比例函数解析式是关键.
11.给某气球充满一定质量的气体,在温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压超过150kPa时,气球会爆炸.由此可判断V=0.04时,气球 不会 爆炸.(用“会”或“不会”填空)
【点拨】设P=,将A(2,2.4)代入求出k=4.8,求得P=,由P>150KPa时,气球将爆炸,得到P≤150,即P=≤150,求得V≥=0.032(m3).因为0.032<0.04,于是得到气球不会爆炸.
【解析】解:设P=,将A(2,2.4)代入求出k=4.8,
∴P=,
当P>150KPa时,气球将爆炸,
∴P≤150,即P=≤150,
解得V≥=0.032(m3).
∵0.032<0.04,
∴气球不会爆炸,
故答案为:不会.
【点睛】本题考查了反比例函数的实际应用,关键是建立函数关系式,并会运用函数关系式解答题目的问题.
12.如图,菱形ABCO的顶点O是坐标原点,点A在反比例函数的图象上,点B在x轴上.若菱形ABCO的面积是8,则k的值为 ﹣4 .
【点拨】根据反比例函数k值几何意义解答即可.
【解析】解:如图,作AD⊥x轴,垂足为D,
∵S菱形ABCO=8,
∴S△ABO=4,
∵AB=AO,AD⊥BO,
∴S△AOD=2,
∴|k|=2S△AOD=4,
∵反比例函数图象在第二象限,
∴k=﹣4.
故答案为:﹣4.
【点睛】本题考查了反比例函数k值的几何意义,熟练掌握该知识点是关键.
13.如图,点在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是7,则k的值为 12 .
【点拨】先根据反比例函数的图象在第一象限判断出k的符号,再延长线段BA,交y轴于点E,由于AB∥x轴,所以AE⊥y轴,故四边形AEOD是矩形,由于点A在双曲线y=上,所以S矩形AEOD=5,同理可得S矩形OCBE=k,由S矩形ABCD=S矩形OCBE﹣S矩形AEOD即可得出k的值.
【解析】解:∵双曲线y=(k≠0)在第一象限,
∴k>0,
延长线段BA,交y轴于点E,
∵AB∥x轴
∴AE⊥y轴,
∴四边形AEOD是矩形,
∵点在双曲线y=上,
∴S矩形AEOD=5,
同理S矩形OCBE=k,
∵S矩形ABCD=S矩形OCBE﹣S矩形AEOD=k﹣5=7,
∴k=12.
故答案为12.
【点睛】本题考查的是反比例函数系数k的几何意义,即在反比例函数y=图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
14.如图,一次函数y=kx+b与反比例函数的图象相交于点A、点B,与x轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ﹣3 ,n= 1 .
(2)求一次函数的解析式和△AOB的面积
(3)根据图象回答:当x为何值时,(请直接写出答案) ﹣3<x<﹣1 .
【点拨】(1)将A点坐标,B点坐标代入解析式可求m,n的值
(2)用待定系数法可求一次函数解析式,根据S△AOB=S△AOC﹣S△BOC可求△AOB的面积.
(3)由图象直接可得.
【解析】解:(1)∵反比例函数的图象过点A(﹣1,3),B(﹣3,n)
∴m=3×(﹣1)=﹣3,m=﹣3n
∴n=1
故答案为﹣3,1
(2)设一次函数解析式y=kx+b,且过(﹣1,3),B(﹣3,1)
∴解得:
∴一次函数的解析式为y=x+4
∵一次函数图象与x轴交点为C
∴0=x+4
∴x=﹣4
∴C(﹣4,0)
∵S△AOB=S△AOC﹣S△BOC
∴S△AOB=×4×3﹣×4×1=4
(3)∵,即kx+b>,
∴一次函数图象在反比例函数图象上方,
∴﹣3<x<﹣1
故答案为﹣3<x<﹣1.
【点睛】本题考查了反比例函数与一次函数的交点问题,待定系数法,利用函数图象上的点满足函数关系式解决问题是本题关键.
15.中国面食文化至今已有两千多年的历史(面条在东汉称之为“煮饼”).厨师将一定质量的面团做成拉面时,面条的总长度y(m)是面条横截面面积S(mm2)的反比例函数,其图象经过A(4,32),B(a,80)两点(如图).
(1)求y与S之间的函数关系式及a的值;
(2)某厨师拉出的面条最细时的横截面面积不超过0.8mm2,求这根面条的总长度至少有多长.
【点拨】(1)设y与x之间的函数表达式为:,将(4,32)代入可得解析式,再把将(a,80)代入解析式可得a的值;
(2)厨师做出的面条横截面面积不超过0.8mm2,可得列式得,解不等式即可.
【解析】解:(1)设y与x之间的函数表达式为:,
由条件可得:k=128,
∴y与S之间的函数表达式为:;
将(a,80)代入可得a=1.6;
(2)由条件可知,
故面条的总长度至少为160m.
【点睛】本题主要考查反比例函数的运用,求不等式的解集,掌握待定系数法求解析式,反比例函数图象的性质,求不等式的解集是解题的关键.
16.驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得,成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 y=100x(0≤x≤4) ;下降阶段的函数解析式为 y=(4≤x≤10) ;(并写出x的取值范围)
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
【点拨】(1)当0≤x≤4时,设直线解析式为:y=kx,当4≤x≤10时,设反比例函数解析式为:y=,利用待定系数法即可解决问题;
(2)分别求出y=200时的两个函数值,再求时间差即可解决问题.
【解析】解:(1)当0≤x≤4时,设直线解析式为:y=kx,将(4,400)代入得:400=4k,
解得:k=100,故直线解析式为:y=100x,
当4≤x≤10时,设反比例函数解析式为:y=,将(4,400)代入得:400=,
解得:a=1600,故反比例函数解析式为:y=;
因此血液中药物浓度上升阶段的函数关系式为y=100x(0≤x≤4),
下降阶段的函数关系式为y=(4≤x≤10).
故答案为:y=100x(0≤x≤4),y=(4≤x≤10);
(2)当y=200,则200=100x,
解得:x=2,
当y=200,则200=,
解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于200微克/毫升的持续时间6小时.
【点睛】本题考查一次函数的应用、反比例函数的应用等知识,解题的关键是灵活应用待定系数法解决问题,学会利用函数图象解决实际问题,属于中考常考题型.
17.如图,点A在反比例函数y1=(x>0)的图象上,B、C两点在反比例函数y2=的图象上,BC经过原点,AB⊥x轴,若△ABC的面积为4,则k的值为 ﹣3 .
【点拨】设A(a,),B(a,),根据BC经过原点,且B、C两点在反比例函数y2=的图象上,得到点B和点C关于原点对称,求得C(﹣a,﹣),根据三角形的面积公式列方程即可得到结论.
【解析】解:设A(a,),
∵AB⊥x轴,
∴B(a,),
∵BC经过原点,且B、C两点在反比例函数y2=的图象上,
∴点B和点C关于原点对称,
∴C(﹣a,﹣),
∵AB=﹣=,△ABC的面积为4,
∴××2a=4,
∴k=﹣3,
故答案为:﹣3,
解法二:连接OA,设AB于x轴交于M,
∵BC经过原点,
∴C,B关于原点对称,
∴OB=OC,
∵△ABC的面积为4,
∴S△AOB=S△ABC=2,
∵点A在反比例函数y1=(x>0)的图象上,
∴OM AM=1,
∴S△BOM=S△AOB﹣S△AOM=2﹣OM AB=,
∴OM BM=2S△BMO=3,
即|k|=3,
∵k<0,
∴k=﹣3.
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数的性质,三角形的面积的计算,熟练掌握反比例函数的性质是解题的关键.
18.在平面直角坐标系中,直线y=x﹣3与双曲线的图象交于点P(a,b),则代数式的值为 ﹣ .
【点拨】由题意得ab=21,b=a﹣3,即可求解.
【解析】解:∵函数y=(x>0)与y=x﹣3的图象交于点P(a,b),
∴ab=21,b=a﹣3,
∴b﹣a=﹣3,
∴==﹣,
故答案为:﹣.
【点睛】此题主要考查了一次函数图象上点的坐标特征以及反比例函数图象上点的特征,正确得出a、b之间的关系是解题关键.
19.若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= ﹣4 .
【点拨】由直线y=﹣2x与反比例函数的图象都关于原点对称,可得(x1,y1),(x2,y2)两点也关于原点对称,则有x2=﹣x1,y2=﹣y1,再代入(y2﹣y1)(x1﹣x2)=16整理得x1y1=﹣4,再利用反比例函数的解析式即可求解.
【解析】解:∵直线y=﹣2x的图象与反比例函数的图象都关于原点对称,且交于(x1,y1),(x2,y2)两点,
∴x2=﹣x1,y2=﹣y1,
由条件可知(﹣y1﹣y1)(x1+x1)=16,
整理得:x1y1=﹣4,
∵(x1,y1)在反比例函数的图象上,
∴k=x1y1=﹣4.
故答案为:﹣4.
【点睛】本题考查了一次函数与反比例函数的交点问题,熟练掌握一次函数与反比例函数的图象与性质是解题的关键.
20.已知函数,函数y2=k2x+b(k1,k2,b是常数,且k1k2≠0).
(1)若函数y1和函数y2的图象交于点A(1,m)和点B(3,1).
①求函数y1,y2的解析式;
②若O为平面直角坐标系的原点,直接写出△AOB的面积;
(2)若点C(2,n)在函数y1的图象上,将点C先向下平移2个单位长度,再向左平移4个单位长度得点D,点D恰好落在函数y1的图象上,求n的值.
【点拨】(1)①利用待定系数法求函数解析式;
②利用函数图象,结合反比例函数的几何意义,可得S△AOB=S梯形ACDB=(AC+BD)×CD=(3+1)×2=4,进而可以得解;
(2)根据平移确定点D的坐标,然后利用函数图象上点的坐标特征代入求解.
【解析】解:(1)①由题意,把点B(3,1)代入,
∴.
∴k1=3.
∴函数y1的表达式为.
把点A(1,m)代入,
∴m=3.
把点A(1,3),点B(3,1)代入y2=k2x+b,
∴.
∴.
∴函数y2的表达式为y2=﹣x+4.
②如图,由(1)得,A(1,3),点B(3,1),
∴AC=3,BD=1,CD=2.
由题意,根据反比例函数的几何意义可得,S△AOB=S梯形ACDB=(AC+BD)×CD=(3+1)×2=4.
(2)由平移,∵C(2,n)在函数y1的图象上,
∴D(﹣2,n﹣2).
∴﹣2(n﹣2)=2n.
∴n=1.
【点睛】本题主要考查了反比例函数与一次函数的交点问题,解题时要熟练掌握并能灵活运用反比例函数的几何意义进行分析是关键.
21.心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
【点拨】(1)从图象上看,AB表示的函数为一次函数,BC是平行于x轴的线段,CD为双曲线的一部分,设出解析式,代入数值可以解答,把自变量的值代入相对应的函数解析式,求出对应的函数值比较得出;
(2)求出相对应的自变量的值,代入相对应的函数解析式,求出注意力指标数与40相比较,得出答案.
【解析】解:(1)设yAB=k1x+b,把(0,20),(10,50)代入函数解析式解得yAB=3x+20(0≤x≤10),
由图象直接得到yBC=50(10≤x≤30),
设yCD=,把(30,50)代入函数解析式解得yCD=(30≤x≤45);
把x=5代入yAB=3x+20,得yAB=35,
把x=35代入yCD=,得yCD=,
因为yAB≤yCD,
所以第35分钟时学生的注意力更集中;
(2)由题意知,注意力指数不低于40
即当在3x+20≥40,x≥
同时≥40
即x≤=37.5
即当开始上课分钟直至上课37.5分钟时学生的注意力指数均不小于40.
而37.5﹣>30,
∴该学习设计合理.
【点睛】此题主要考查了反比例函数的应用,此题属于分段函数,根据实际情况,结合图象,求出相对应的函数解析式,计算出数值,代入相应的函数解析式解决问题.
22.在反比例函数y=(x>0)的图象上,有一系列点A1,A2,A3,…,An,An+1,若A1的横坐标为2,以后每个点的横坐标与它前一个点的横坐标的差都为2,过A1,A2,A3,…,An,An+1分别作x轴与y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn= .
【点拨】由已知条件横坐标成等差数列,再根据点A1、A2、A3、…、An、An+1在反比例函数上,求出各点坐标,即可求出S1,S2,S3,进而求出S1+S2+S3+…+Sn,即可作答.
【解析】解:∵点A1、A2、A3、…、An、An+1都在反比例函数的图象上,且A1的横坐标为2,
则,
∴A1(2,6),
由条件可知,
∴A2(4,3)、
则,
∴A3(6,2),
依次类推得,
∴S1=2×(6﹣3),
S2=2×(3﹣2),
,
……,
,
∴S1+S2+S3+…+Sn
=
=
=.
故答案为:.
【点睛】本题主要考查了反比例函数的性质,坐标规律探索,发现规律是关键.
23.如图,在平面直角坐标系xOy中,一次函数y1=kx+b的图象与反比例函数的图象交于点A,B,点A的横坐标为2,当x<﹣3时,总有y2>y1恒成立,则k的取值范围是 k≥1 .
【点拨】首先确定点A的坐标(2,3),由一次函数y=kx+b经过点A,推出3=2k+b,推出b=3﹣2k,推出一次函数的解析式为y=kx+3﹣2k,再构建不等式求解.
【解析】解:∵点A在y=的图象上,横坐标是2,
∴A(2,3),
∵一次函数y=kx+b经过点A,
∴3=2k+b,
∴b=3﹣2k,
∴一次函数的解析式为y=kx+3﹣2k,
由题意当x<﹣3时,总有y2>y1恒成立,
∴﹣2≥﹣3k+3﹣2k,
∴k≥1.
故答案为:k≥1.
【点睛】本题考查反比例函数与一次函数的交点,解题的关键是理解题意,灵活运用所学知识解决问题.
24.如图,已知正比例函数图象经过点A(4,2),B(m,3).
(1)正比例函数的解析式是 ,m的值是 6 ;
(2)分别过点A与点B作y轴的平行线,与反比例函数在第一象限的分支分别交于点C、D(点C、D均在点A、B下方),若BD:AC=7:3,求反比例函数的解析式;
(3)在第(2)小题的前提下,联结BC,若点E是反比例函数在第一象限的图象上位于点C左侧的一点,且△ABE的面积是△ABC面积的2倍,求点E的坐标.
【点拨】(1)用待定系数法即可求解;
(1)BD:AC=7:3,即(6﹣):(4﹣)=7:3,即可求解;
(3)过点C作AB的平行线CN交y轴于点N,如图,取OM=2ON,过点M作ME∥AB交反比例函数于点E,即可求解.
【解析】解:(1)设正比例函数的表达式为:y=tx,
将点A、B的坐标代入上式得:2=4t,3=mt,
解得:t=,m=6,
故答案为:,6;
(1)由(1)知,正比例函数的表达式为:y=x,点B(3,6),
设反比例函数的解析式的表达式为:y=,
设点C(4,),B(6,),
∵BD:AC=7:3,即(6﹣):(4﹣)=7:3,
解得:k=4,
则反比例函数的表达式为:y=;
(3)过点C作AB的平行线CN交y轴于点N,如图,取OM=2ON,过点M作ME∥AB交反比例函数于点E,
则此时,△ABE的面积是△ABC面积的2倍,
∵CN∥AB∥ME,
故直线CN的表达式为:y=(x﹣4)+1,则点N(0,﹣1),即ON=1,则OM=2,
即点M(0,2),则直线ME的表达式为:y=x+2,
联立上式和反比例函数的表达式得:=x+2,
解得:x=﹣2+2(负值已舍去),
即点E(﹣2+2,).
【点睛】本题为反比例函数综合运用,涉及到平行线的性质,面积的计算、求函数表达式等,利用平行线的性质确定面积之间的关系是解题的关键.
25.如图,在平面直角坐标系中,点O是坐标原点,一次函数y1=kx+b与反比例函数(x>0)的图象交于A(2,m)、B(4,2)两点.
(1)求一次函数y1与反比例函数y2的解析式;
(2)根据图象回答,当时,x的取值范围为 0<x≤2或x≥4 ;
(3)y轴上有一点P,当以点O、P、A、B为顶点的四边形的面积为7时,求点P的坐标.
【点拨】(1)把B(4,2)代得2=,解方程得到反比例函数y2的解析式为y2=,把A(2,m)代入y2=得,m==4,求得A(2,4),把A(2,4),B(4,2)代入y1=kx+b得解方程组得到一次函数y1的解析式为y1=﹣x+6;
(2)根据函数图象即可得到不等式的解集;
(3)设P(0,a),解方程得到M(0,6),N(6,0),根据三角形的面积公式即可得到结论.
【解析】解:(1)把B(4,2)代得2=,
∴n=8,
∴反比例函数y2的解析式为y2=,
把A(2,m)代入y2=得,m==4,
∴A(2,4),
把A(2,4),B(4,2)代入y1=kx+b得,,
∴,
∴一次函数y1的解析式为y1=﹣x+6;
(2)由图象得,当时,x的取值范围为0<x≤2或x≥4;
故答案为:0<x≤2或x≥4;
(3)设P(0,a),
在y1=﹣x+6中,当x=0时,y=6,当y=0时,x=6,
∴M(0,6),N(6,0),
∴S四边形ABOP=S△MON﹣S△APM﹣S△OBN=﹣×(6﹣a)×2﹣×6×2=7或S四边形AOPB=S△MON﹣S△AOM﹣S△OBN+S△OBP=﹣×6×2﹣×6×2+×(﹣a)×4=7
∴a=1或﹣0.5,
∴点P的坐标为(0,1)或(0,﹣0.5).
【点睛】本题是反比例函数综合题,考查了待定系数法求函数的解析式,三角形的面积,正确地求出函数的解析式是解题的关键.
26.如图,直线AB与反比例函数的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)连接OA、OB,求△OAB的面积;
(3)是否存在x轴上的一个动点P,使PA+PB最小,若存在求出P点坐标,若不存在,请说明理由.
【点拨】(1)把A(1,4)代入y= 中,求出m的值,即可得反比例函数解析式为y=;
(2)分别过点A、B作AC⊥x轴,交x轴于点C、交OB于点E,过点B作BD⊥x轴,交x轴于点D.先求出B点的坐标为B(4,1).由反比例函数的几何意义可得S△OAC=S△OBD==2,则可得S△OAE=S梯形CEBD,进而可得S△OAB=S梯形ACDB,根据梯形的面积公式即可求解;
(3)作点A关于x轴的对称点A′,连接A′B交x轴于P,此时PA+PB的值最小.求出A′B的表达式为y=x﹣,再求出y=0时x的值,即可得P点的坐标.
【解析】解:(1)把A(1,4)代入y=得m=1×4=4,
∴反比例函数解析式为y=;
(2)分别过点A、B作AC⊥x轴,交x轴于点C、交OB于点E,过点B作BD⊥x轴,交x轴于点D,如图1,
由(1)可知,反比例函数解析式为y=,
把B(4,n)代入y=,得4n=4,
解得n=1,
∴B(4,1).
∵S△OAC=S△OCE+S△OAE==2,S△OBD=S△OCE+S梯形CEBD==2,
∴S△OAE=S梯形CEBD,
∵S△OAB=S△OAE+S△ABE,
∴S△OAB=S梯形CEBD+S△ABE=S梯形ACDB,
∴S△OAB=(|yA|+|yB|)(xB﹣xA)=×(4+1)×(4﹣1)=;
(3)存在x轴上的一个动点P,使PA+PB最小;理由如下:
作点A关于x轴的对称点A′,如图,则A′(1,﹣4),连接A′B交x轴于P,则PA=PA′,
∴PA+PB=PA′+PB=A′B,
∴此时PA+PB的值最小,
设直线A′B的解析式为y=kx+b,
把A′(1,﹣4),B(4,1)代入得:
,
解得,
∴直线A′B的解析式为y=x﹣,
当y=0时,x﹣=0,
解得x=,
∴P点坐标为(,0).
【点睛】本题属于反比例函数综合题,主要考查了用待定系数法求反比例函数的表达式、反以及反比例函数的几何意义以及利用将军饮马求点的坐标.熟练掌握反比例函数k的几何意义是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
