4.1 比例线段 练习 浙教版(2024)数学九年级上册
文档属性
| 名称 | 4.1 比例线段 练习 浙教版(2024)数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 231.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 12:54:23 | ||
图片预览



文档简介
4.1 比例线段 练习
一、选择题
1.若,则( )
A. B. C. D.
2.下列各组线段中是成比例线段的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,2cm,4cm
C.3cm,5cm,9cm,13cm D.1cm,2cm,2cm,3cm
3.根据,可以组成的比例有( )
A. B. C. D.
4.若,且b是a,c的比例中项,则等于( )
A.1∶3 B.1∶2 C.2:3 D.2∶1
5.如图,点是线段的黄金分割点,,则的长为( )
A. B. C. D.
6.采用如下方法可以得到黄金分割点:如图,是已知线段,经过点作,使,连接,在上截取;在截取,点就是线段的黄金分割点.若,则( )
A. B. C. D.
7.两千多年前,古希腊数学家欧多克索斯发现:如图,点将一条线段分割成长、短两条线段、,若较短线段与较长线段的长度之比等于较长线段的长度与全长之比,这种分割称为黄金分割,这个点叫做线段的黄金分割点.主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设她至少走米(的长为米)时恰好站在舞台的黄金分割点上,则满足的方程是( )
A. B. C. D.
8.若(b、d、f均为正数),则下列式子不一定成立的是( )
A. B.
C. D.
9.已知,并且,则函数图像一定经过( )
A.第一、二、三象限 B.第二、三象限
C.第二、三、四象限 D.第一、四象限
10.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1 与S2的大小关系是( )
A. B. C. D.1
二、填空题
11.已知线段,线段,则线段,的比例中项线段的长度为 .
12.已知,且,那么 .
13.在比例尺为的地图上,A,B两地间的图上距离为2厘米,则A,B两地间的实际距离是 千米.
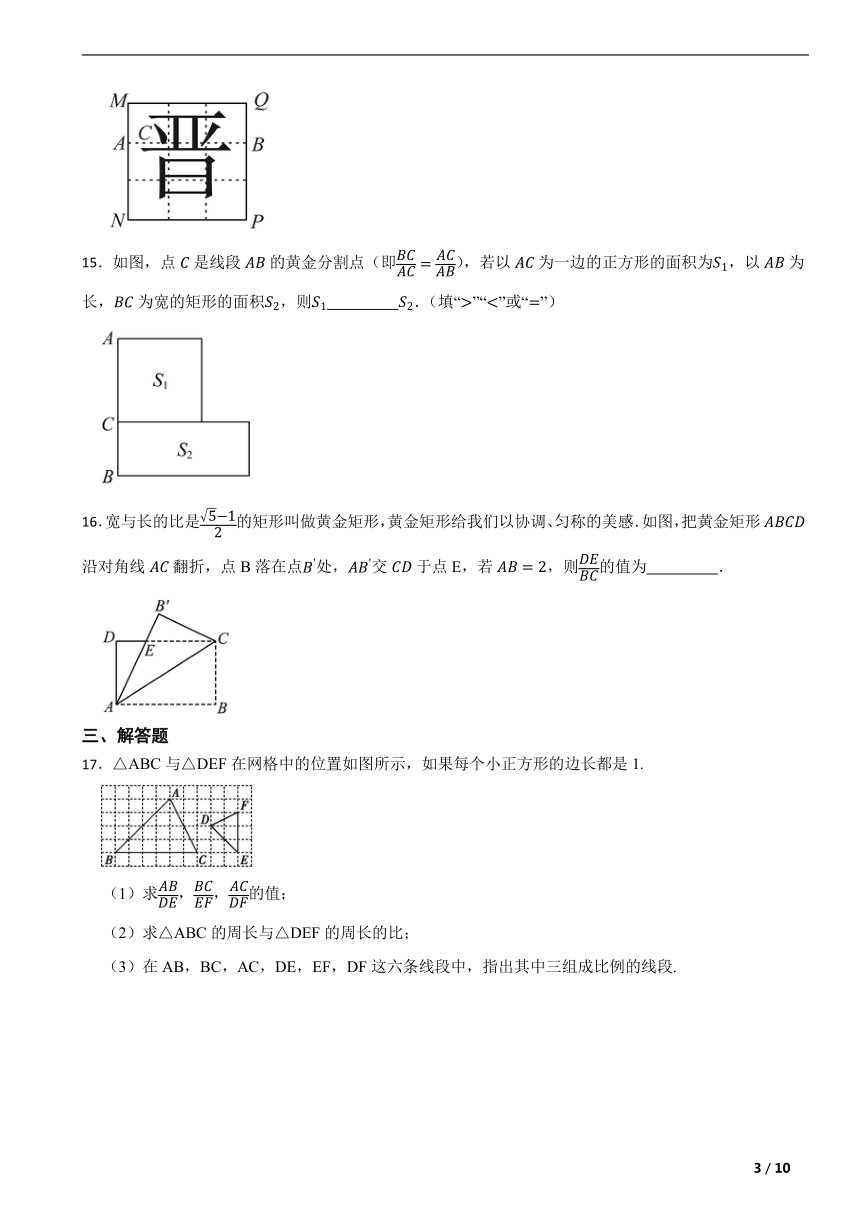
14.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边上,且,“晋”字的笔画“、”的位置在的黄金分割点C处,且,若,则的长为 (结果保留根号).
15.如图,点是线段的黄金分割点(即),若以为一边的正方形的面积为,以为长,为宽的矩形的面积,则 .(填“”“”或“”)
16.宽与长的比是的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.如图,把黄金矩形沿对角线翻折,点B落在点处,交于点E,若,则的值为 .
三、解答题
17.△ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1.
(1)求,,的值;
(2)求△ABC的周长与△DEF的周长的比;
(3)在AB,BC,AC,DE,EF,DF这六条线段中,指出其中三组成比例的线段.
18.已知,求代数式的值.
19.已知线段,,满足.
(1)求的值.
(2)当线段是线段,的比例中项,且时,求的值.
20.如图,在平行四边形ABCD中,DE⊥AB于点E,BF⊥AD交AD的延长线于点F.
(1)AB,BC,BF,DE这四条线段能否成比例 如能,请写出比例式;如不能,请说明理由.
(2)若AB=10,DE=2.5,BF=5,求BC的长.
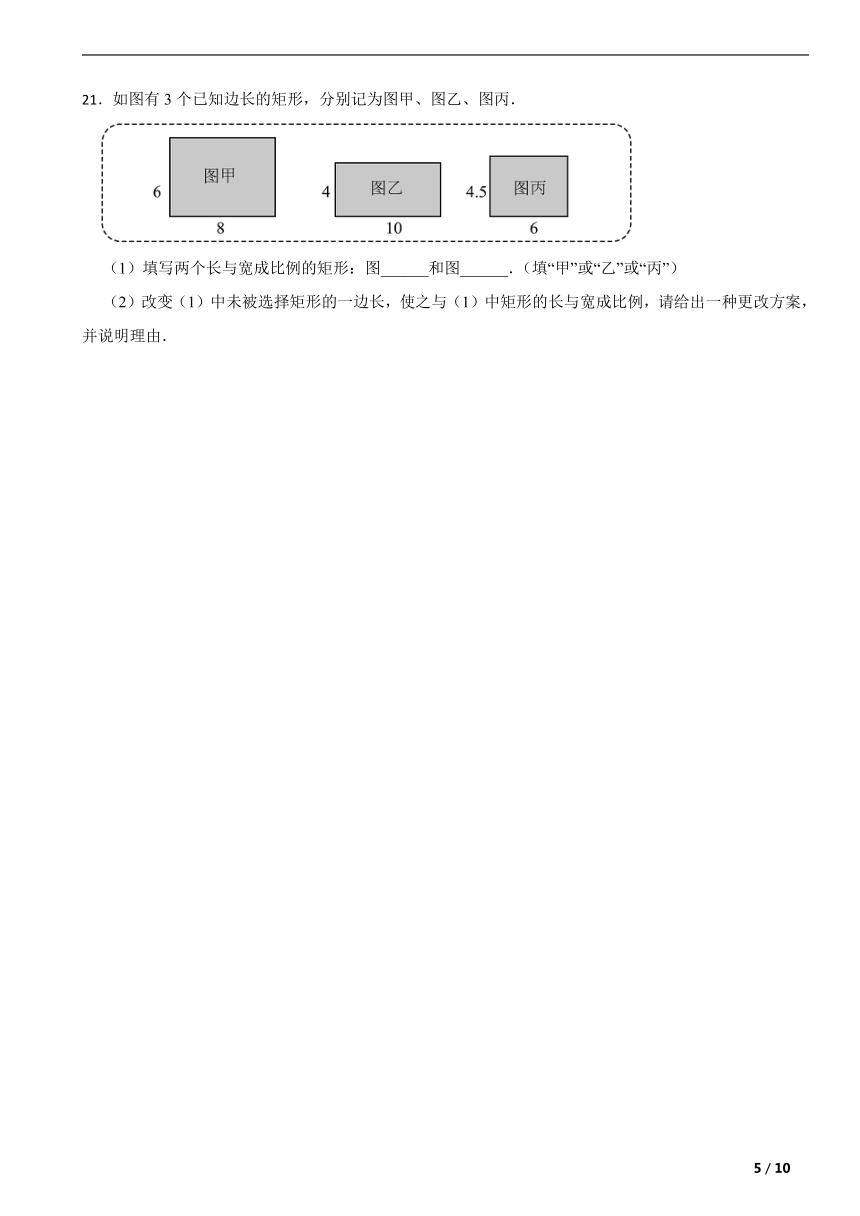
21.如图有3个已知边长的矩形,分别记为图甲、图乙、图丙.
(1)填写两个长与宽成比例的矩形:图______和图______.(填“甲”或“乙”或“丙”)
(2)改变(1)中未被选择矩形的一边长,使之与(1)中矩形的长与宽成比例,请给出一种更改方案,并说明理由.
22.综合与实践
【问题提出】
勾股定理和黄金分割是几何学中的两大瑰宝,其中"贵金分割"给人以美感.课本第56页这样定义"黄金分割点":如图1,点将线段AB分成两部分,若,则称点为线段AB的黄金分割点,这个比值称为黄金比.
(1)【初步感知】
如图1,若,求临金比的值.
(2)【类比探究】
如图2,在中,是BC边上一点,AD将分割成两个三角形(),若,则称AD为的黄金分割线.
①求证:点D是线段BC的黄金分割点:
②若△ABC的面积为4,求△ACD的面积.
参考答案
1.A
2.B
3.A
4.B
5.B
6.C
7.A
8.B
9.B
解:因为,
所以
所以,
①当a+b+c不等于0时,,
所以3=p+1,解得:则,
直线经过一、二、三象限(如图).
②当a+b+c=0时,p+1=0,解得p=-1,
则y=-x-1,
直线y=-x-1经过二、三、四象限(如图),
综上:的图像一定经过二、三象限;
10.D
解:设正方形ABCD边长为a,
∵四边形ABCD为正方形,
∴∠EAB=90°,
∵点E为AD中点,
∴AE=,
在Rt△EAB中,
∴BE=a,
∵EF=BE,
∴EF=a,
∴AF=EF-AE=a-a=a,
∴正方形AFGH边长为a,
∴S1=S正AFGH=(a)2=a2,
∵AH=a,AB=a,
∴BH=AB-AH=a-a=a,
∴S2=S正BCEH=a·a=a2,
∴S1=S2.
11.
12.5
13.180
14.或
15.
16.
17.(1)===2.
(2)2.
(3)解:①∵AB∶DE=BC∶EF,∴AB,DE,BC,EF是成比例线段.②∵AB∶DE=AC∶DF,AB,DE,AC,DF是成比例线段.③∵BC∶EF=AC∶DF,∴BC,EF,AC,DF是成比例线段.
18.2
19.(1).
(2).
20.(1)解:能.∵在平行四边形ABCD中,DE⊥AB,BF⊥AD,
∴SABCD=AB·DE=AD·BF,
∴
∵AD=BC,∴
(2)解:由(1)得,AB·DE=BC·BF,
∴10×2.5=5BC,解得BC=5.
21.(1)甲,丙;
(2)图乙中,长减少7时,与(1)中矩形的长与宽成比例.
22.(1)解:如图1, 设 则.
,
,
,
整理得:
解得 (不符合题意,舍去) ,
,
,
∴黄金比 的值为
(2)①证明: 如图2, 作 '于点R,
且,
∴,
,
∴点D是线段BC的黄金分割点.
②,
,
的面积是
1 / 1
一、选择题
1.若,则( )
A. B. C. D.
2.下列各组线段中是成比例线段的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,2cm,4cm
C.3cm,5cm,9cm,13cm D.1cm,2cm,2cm,3cm
3.根据,可以组成的比例有( )
A. B. C. D.
4.若,且b是a,c的比例中项,则等于( )
A.1∶3 B.1∶2 C.2:3 D.2∶1
5.如图,点是线段的黄金分割点,,则的长为( )
A. B. C. D.
6.采用如下方法可以得到黄金分割点:如图,是已知线段,经过点作,使,连接,在上截取;在截取,点就是线段的黄金分割点.若,则( )
A. B. C. D.
7.两千多年前,古希腊数学家欧多克索斯发现:如图,点将一条线段分割成长、短两条线段、,若较短线段与较长线段的长度之比等于较长线段的长度与全长之比,这种分割称为黄金分割,这个点叫做线段的黄金分割点.主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设她至少走米(的长为米)时恰好站在舞台的黄金分割点上,则满足的方程是( )
A. B. C. D.
8.若(b、d、f均为正数),则下列式子不一定成立的是( )
A. B.
C. D.
9.已知,并且,则函数图像一定经过( )
A.第一、二、三象限 B.第二、三象限
C.第二、三、四象限 D.第一、四象限
10.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1 与S2的大小关系是( )
A. B. C. D.1
二、填空题
11.已知线段,线段,则线段,的比例中项线段的长度为 .
12.已知,且,那么 .
13.在比例尺为的地图上,A,B两地间的图上距离为2厘米,则A,B两地间的实际距离是 千米.
14.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边上,且,“晋”字的笔画“、”的位置在的黄金分割点C处,且,若,则的长为 (结果保留根号).
15.如图,点是线段的黄金分割点(即),若以为一边的正方形的面积为,以为长,为宽的矩形的面积,则 .(填“”“”或“”)
16.宽与长的比是的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.如图,把黄金矩形沿对角线翻折,点B落在点处,交于点E,若,则的值为 .
三、解答题
17.△ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1.
(1)求,,的值;
(2)求△ABC的周长与△DEF的周长的比;
(3)在AB,BC,AC,DE,EF,DF这六条线段中,指出其中三组成比例的线段.
18.已知,求代数式的值.
19.已知线段,,满足.
(1)求的值.
(2)当线段是线段,的比例中项,且时,求的值.
20.如图,在平行四边形ABCD中,DE⊥AB于点E,BF⊥AD交AD的延长线于点F.
(1)AB,BC,BF,DE这四条线段能否成比例 如能,请写出比例式;如不能,请说明理由.
(2)若AB=10,DE=2.5,BF=5,求BC的长.
21.如图有3个已知边长的矩形,分别记为图甲、图乙、图丙.
(1)填写两个长与宽成比例的矩形:图______和图______.(填“甲”或“乙”或“丙”)
(2)改变(1)中未被选择矩形的一边长,使之与(1)中矩形的长与宽成比例,请给出一种更改方案,并说明理由.
22.综合与实践
【问题提出】
勾股定理和黄金分割是几何学中的两大瑰宝,其中"贵金分割"给人以美感.课本第56页这样定义"黄金分割点":如图1,点将线段AB分成两部分,若,则称点为线段AB的黄金分割点,这个比值称为黄金比.
(1)【初步感知】
如图1,若,求临金比的值.
(2)【类比探究】
如图2,在中,是BC边上一点,AD将分割成两个三角形(),若,则称AD为的黄金分割线.
①求证:点D是线段BC的黄金分割点:
②若△ABC的面积为4,求△ACD的面积.
参考答案
1.A
2.B
3.A
4.B
5.B
6.C
7.A
8.B
9.B
解:因为,
所以
所以,
①当a+b+c不等于0时,,
所以3=p+1,解得:则,
直线经过一、二、三象限(如图).
②当a+b+c=0时,p+1=0,解得p=-1,
则y=-x-1,
直线y=-x-1经过二、三、四象限(如图),
综上:的图像一定经过二、三象限;
10.D
解:设正方形ABCD边长为a,
∵四边形ABCD为正方形,
∴∠EAB=90°,
∵点E为AD中点,
∴AE=,
在Rt△EAB中,
∴BE=a,
∵EF=BE,
∴EF=a,
∴AF=EF-AE=a-a=a,
∴正方形AFGH边长为a,
∴S1=S正AFGH=(a)2=a2,
∵AH=a,AB=a,
∴BH=AB-AH=a-a=a,
∴S2=S正BCEH=a·a=a2,
∴S1=S2.
11.
12.5
13.180
14.或
15.
16.
17.(1)===2.
(2)2.
(3)解:①∵AB∶DE=BC∶EF,∴AB,DE,BC,EF是成比例线段.②∵AB∶DE=AC∶DF,AB,DE,AC,DF是成比例线段.③∵BC∶EF=AC∶DF,∴BC,EF,AC,DF是成比例线段.
18.2
19.(1).
(2).
20.(1)解:能.∵在平行四边形ABCD中,DE⊥AB,BF⊥AD,
∴SABCD=AB·DE=AD·BF,
∴
∵AD=BC,∴
(2)解:由(1)得,AB·DE=BC·BF,
∴10×2.5=5BC,解得BC=5.
21.(1)甲,丙;
(2)图乙中,长减少7时,与(1)中矩形的长与宽成比例.
22.(1)解:如图1, 设 则.
,
,
,
整理得:
解得 (不符合题意,舍去) ,
,
,
∴黄金比 的值为
(2)①证明: 如图2, 作 '于点R,
且,
∴,
,
∴点D是线段BC的黄金分割点.
②,
,
的面积是
1 / 1
同课章节目录
