4.5 相似三角形的性质及其应用 (第一课时)同步练习(含答案)
文档属性
| 名称 | 4.5 相似三角形的性质及其应用 (第一课时)同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 206.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览


文档简介
4.5 相似三角形的性质及其应用 第一课时
一、基础巩固
1.如图,,它们的相似比是,已知,则的长是( )
A.4 B. C.5 D.
2.如果两个相似三角形的相似比是,那么这两个相似三角形对应边上的中线之比是( )
A. B. C. D.
3.已知中,,于点D,E是的中点,交于点O,若,则的长是( )
A.5 B. C.6 D.10
4.如图,在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将OAB放大为原来的2倍,得到△OA'B',则△OA'B'的重心坐标是( )
A.(﹣3,1) B.(﹣6,2)
C.(﹣3,1)或(3,﹣1) D.(6,﹣2)或(﹣6,2)
5.如果两个相似三角形的对应边上的高之比为2:3,那么它们的对应中线之比为 .
6.如图,点O是的重心,则 .(填“”“”或“”)
7.已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB,AC于点E,F.求AF:FC和EF:BC的值.
8.已知:如图,在中,,点为的重心.
(1)若,求的值;
(2)联结,若,且,求的面积.
四、提升练习
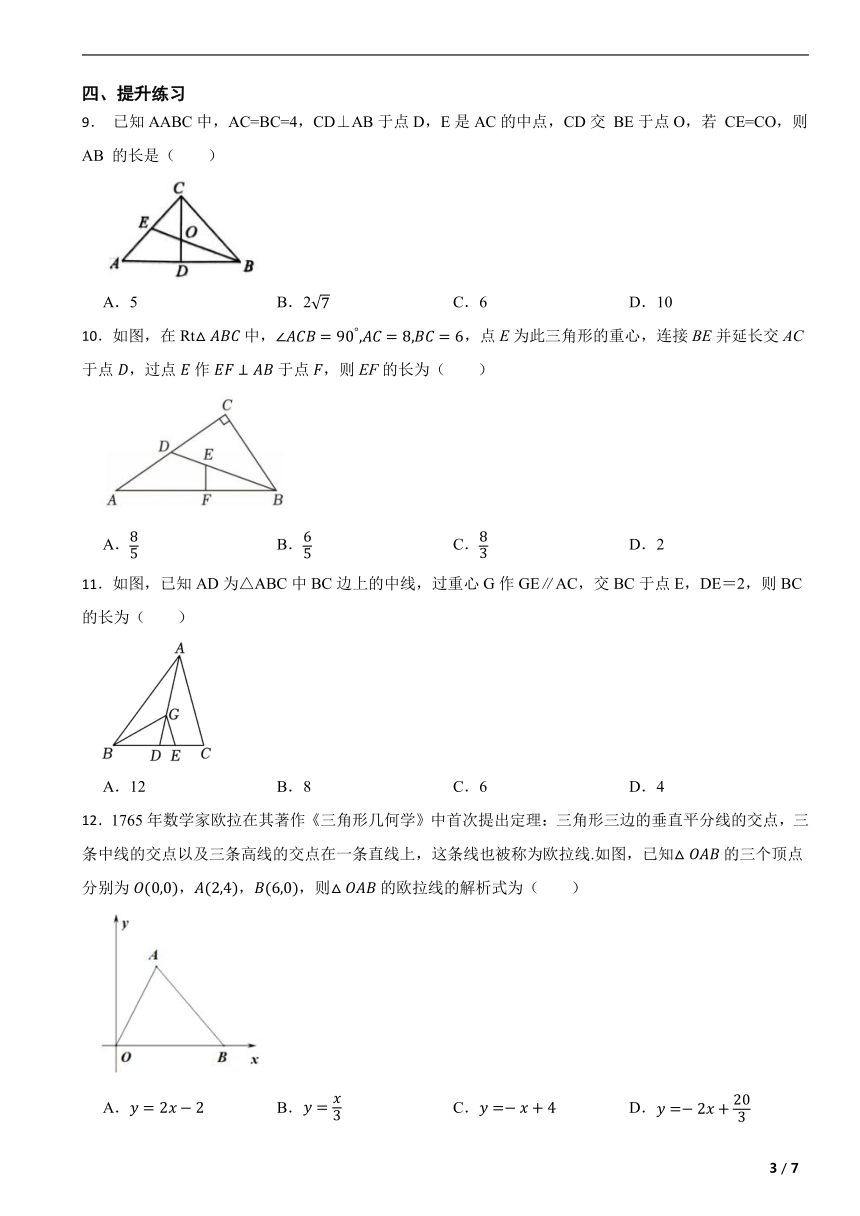
9. 已知AABC中,AC=BC=4,CD⊥AB于点D,E是AC的中点,CD交 BE于点O,若 CE=CO,则AB 的长是( )
A.5 B.2 C.6 D.10
10.如图,在Rt中,,点E为此三角形的重心,连接BE并延长交AC于点,过点作于点,则EF的长为( )
A. B. C. D.2
11.如图,已知AD为△ABC中BC边上的中线,过重心G作GE∥AC,交BC于点E,DE=2,则BC的长为( )
A.12 B.8 C.6 D.4
12.1765年数学家欧拉在其著作《三角形几何学》中首次提出定理:三角形三边的垂直平分线的交点,三条中线的交点以及三条高线的交点在一条直线上,这条线也被称为欧拉线.如图,已知的三个顶点分别为,,,则的欧拉线的解析式为( )
A. B. C. D.
13.如果三角形的每条边都扩大为原来的2倍,那么三角形的每条高都为原来的 倍.
14.已知在 中, , 点 是 的重心, 那么点 到斜边 的距离是 .
15.如图,在中,,,点是的重心,,则的长为 .
16.以一个等腰直角三角形的腰为边分别向形外作等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”,如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .
17.在Rt△ABC中,∠C=90°.
(1)用尺规作图作Rt△ABC的重心P.(保留作图痕迹,不要求写作法和证明);
(2)你认为只要知道Rt△ABC哪一条边的长即可求出它的重心与外心之间的距离?并请你说明理由.
18.如图,在Rt△ABC中,∠ACB=90°,∠B=30°.点O是△ABC的重心,连结CO并延长,交AB于点E,过点E作EF⊥AB,交BC于点F,连结AF,交CE于点M.求的值.
参考答案解
1.D
2.B
3.B
4.D
5.2:3
6.
7.解:∵G是△ABC的重心,且AD是BC边上的中线,
∴AG:GD=2:1,AG:AD=2:3.
∵EF∥BC,
∴AF:FC=AG:GD=2:1,EF:BC=AF:AC=AG:AD=2:3
8.(1);
(2);
9.B
10.C
11.A
12.C
13.2
14.
15.
16.
17.解:(1)如图所示:
(2)知道Rt△ABC中AB的长即可求出它的重心与外心之间的距离.
理由:设AB的中点为O,则O为△ABC的外心,且CO=AB,
∵点P为△ABC的重心,
∴PO=,
∴重心到外心的距离PO=AB.
18.解:∵点O是△ABC的重心,∴OC=CE.在Rt△ACB中,CE=BE=AE,
∴∠FAE=∠B=30°,∠BAC=60°,得△ACE是等边三角形,∴CM=CE,
∴OM=CE-CE=CE,即OM=AE.
在Rt△AEF中,EF=AE,∠AFE=60°,∴∠FEM=30°,∴MF=EF,
∴MF=AE.∴=
1 / 1
一、基础巩固
1.如图,,它们的相似比是,已知,则的长是( )
A.4 B. C.5 D.
2.如果两个相似三角形的相似比是,那么这两个相似三角形对应边上的中线之比是( )
A. B. C. D.
3.已知中,,于点D,E是的中点,交于点O,若,则的长是( )
A.5 B. C.6 D.10
4.如图,在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将OAB放大为原来的2倍,得到△OA'B',则△OA'B'的重心坐标是( )
A.(﹣3,1) B.(﹣6,2)
C.(﹣3,1)或(3,﹣1) D.(6,﹣2)或(﹣6,2)
5.如果两个相似三角形的对应边上的高之比为2:3,那么它们的对应中线之比为 .
6.如图,点O是的重心,则 .(填“”“”或“”)
7.已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB,AC于点E,F.求AF:FC和EF:BC的值.
8.已知:如图,在中,,点为的重心.
(1)若,求的值;
(2)联结,若,且,求的面积.
四、提升练习
9. 已知AABC中,AC=BC=4,CD⊥AB于点D,E是AC的中点,CD交 BE于点O,若 CE=CO,则AB 的长是( )
A.5 B.2 C.6 D.10
10.如图,在Rt中,,点E为此三角形的重心,连接BE并延长交AC于点,过点作于点,则EF的长为( )
A. B. C. D.2
11.如图,已知AD为△ABC中BC边上的中线,过重心G作GE∥AC,交BC于点E,DE=2,则BC的长为( )
A.12 B.8 C.6 D.4
12.1765年数学家欧拉在其著作《三角形几何学》中首次提出定理:三角形三边的垂直平分线的交点,三条中线的交点以及三条高线的交点在一条直线上,这条线也被称为欧拉线.如图,已知的三个顶点分别为,,,则的欧拉线的解析式为( )
A. B. C. D.
13.如果三角形的每条边都扩大为原来的2倍,那么三角形的每条高都为原来的 倍.
14.已知在 中, , 点 是 的重心, 那么点 到斜边 的距离是 .
15.如图,在中,,,点是的重心,,则的长为 .
16.以一个等腰直角三角形的腰为边分别向形外作等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”,如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .
17.在Rt△ABC中,∠C=90°.
(1)用尺规作图作Rt△ABC的重心P.(保留作图痕迹,不要求写作法和证明);
(2)你认为只要知道Rt△ABC哪一条边的长即可求出它的重心与外心之间的距离?并请你说明理由.
18.如图,在Rt△ABC中,∠ACB=90°,∠B=30°.点O是△ABC的重心,连结CO并延长,交AB于点E,过点E作EF⊥AB,交BC于点F,连结AF,交CE于点M.求的值.
参考答案解
1.D
2.B
3.B
4.D
5.2:3
6.
7.解:∵G是△ABC的重心,且AD是BC边上的中线,
∴AG:GD=2:1,AG:AD=2:3.
∵EF∥BC,
∴AF:FC=AG:GD=2:1,EF:BC=AF:AC=AG:AD=2:3
8.(1);
(2);
9.B
10.C
11.A
12.C
13.2
14.
15.
16.
17.解:(1)如图所示:
(2)知道Rt△ABC中AB的长即可求出它的重心与外心之间的距离.
理由:设AB的中点为O,则O为△ABC的外心,且CO=AB,
∵点P为△ABC的重心,
∴PO=,
∴重心到外心的距离PO=AB.
18.解:∵点O是△ABC的重心,∴OC=CE.在Rt△ACB中,CE=BE=AE,
∴∠FAE=∠B=30°,∠BAC=60°,得△ACE是等边三角形,∴CM=CE,
∴OM=CE-CE=CE,即OM=AE.
在Rt△AEF中,EF=AE,∠AFE=60°,∴∠FEM=30°,∴MF=EF,
∴MF=AE.∴=
1 / 1
同课章节目录
