数学:5.4一元一次不等式(第2课时)课件(浙教版八年级上)
文档属性
| 名称 | 数学:5.4一元一次不等式(第2课时)课件(浙教版八年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 220.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-22 00:00:00 | ||
图片预览






文档简介
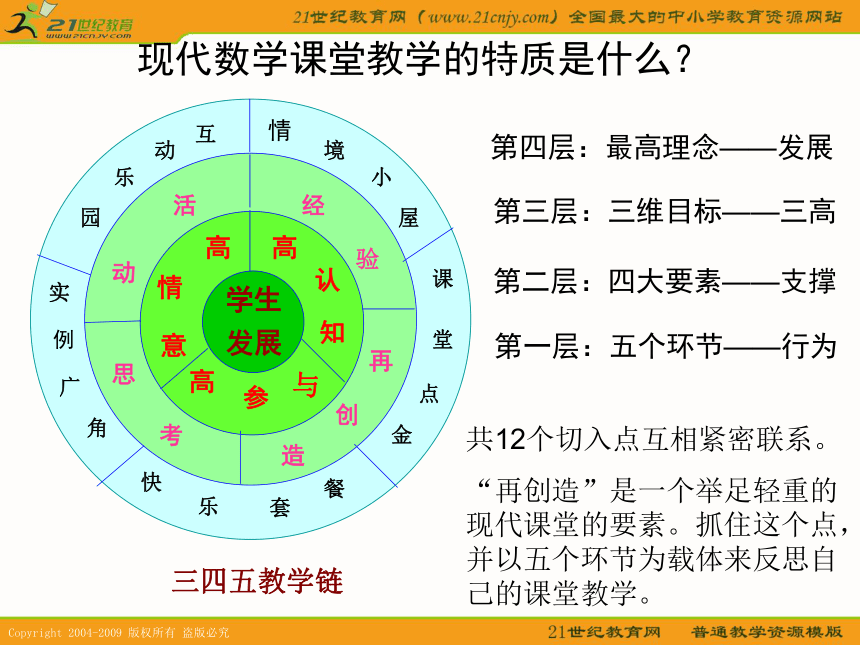
课件20张PPT。——《一元一次不等式组》课堂教学反思 子曰:”学而不思则罔,思而不学则贻”。 为再创造而教 现代数学课堂教学的特质是什么? 三四五教学链例第四层:最高理念——发展
第三层:三维目标——三高
第二层:四大要素——支撑 第一层:五个环节——行为共12个切入点互相紧密联系。
“再创造”是一个举足轻重的现代课堂的要素。抓住这个点,并以五个环节为载体来反思自己的课堂教学。何谓再创造? 遵循数学本身发展和学生认知规律,引导学生在已有的生活经验上,通过师生活动,经历数学发现的过程拓展学生思维,从而实现数学学习目标的现代数学学习方式。三大特点 1.在教育的环境下创造,有别于数学家发现数学;
2.它可以是逻辑思维方法学习,也十分注重合情推理方法学习;
3.它可以是独立学习,也十分重视合作学习;
4.它是教师行为,也是学生行为.教师帮助学生自己帮助自己的学习.数学老师的体重大致在什么范围?信息1:设数学老师的体重为x千克,盛老师的体重小于小明体重(65千克)的2倍还少39.5千克.可列出不等式. 信息2:数学老师的体重的2倍不小于小明体重(65千克)的2倍还多50千克.可列出不等式. x<2×65-39.5, ①2x≥2×65+50. ②
★提出问题 1.单独的不等式①能比较好地确定老师的体重范围吗? 2.单独的不等式②能比较好地确定老师的体重范围吗?3.怎样才能较好地确定老师的体重范围呢?x满足不等式①,且满足不等式②——用大括号组合两个不等式.x<90.5.x≥90.0.建立这个教学环节在于提出问题,引入课题.这个环节,教师舍去了教材提供的引入题.理由是 1.远离学生生活实际的“公司购买商品”,没有很好的联系学生的生活经验;
2.直接给出了不等式组,等于是一种灌输,起不到不等式组产生的实际需要的必然性;
3.无法围绕本课主题内容,让学生带着最本质的问题去学习. 一句话,教材给出的,是数学本身的数学,但不是有利于学生学习创造的数学.而本人在这方面正好弥补了教材的缺陷.(强调要用教材)关于课堂情景的创设(寻求知识固定点)
趣——激发兴趣
疑——问题意识
明——明确主题反思:★观察思考 不等式① ②组合在一起,具有什么特征?
·· (2)两个不等式都是一元一次不等式.(1)含有同一个未知数x;定义一:至少有两个含有同一个未知数的一元一次不等式组成的一组不等式,叫做一元一次不等式组.1.这部分最能体现在创造的价值.观察思考其特点,不是现在的描述性定义让学生去死记.这是再创造的最初要义.
2.创造往往从观察开始,初步认识一元一次不等式组的内涵特征.
3.虽然强调概念内涵特征.但课程标准没有明确对定义的了解,更没有理解的要求.这里能这样点到得出定义就可以了.(熟练解不等式组才是重点)
★活动体验 某校即将举行校庆,一批知名校友将来母校参加典礼活动,需要我班几名女同学做礼仪服务,在身高上有要求.基本条件一:身高要不低于1.60米女同学,基本条件二:身高要低于1.65米女同学. 谁能有机会成为礼仪服务员,为学校做一点微薄的贡献呢?x ≥ 1.60请站起来.身高x满足请站起来.身高x满足x<1.65两次都站起来过的学生再站起来亮相.她们身高x满足再创造除了抽象理性的探究,也要十分重视学生的具体感性体验.
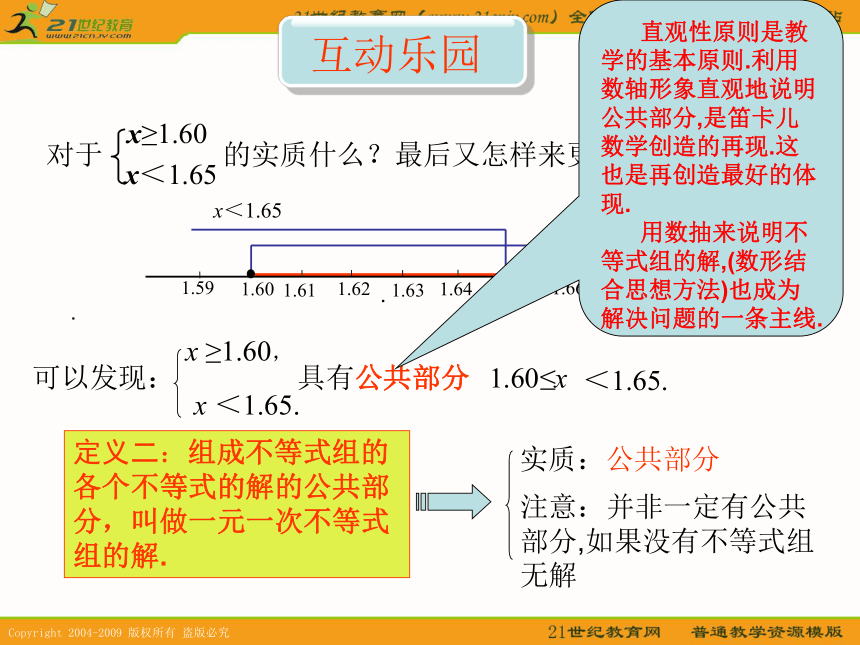
求公共部分是这个内容的难点,也是关键.通过身边的活动的体验性学习,不仅让学生乐于学习,也培养了学生在活动中,去发现问题去认识问题-------不等式组的解其实就是求每一个不等式的公共部分. 1.60≤x<1.65.定义二:组成不等式组的各个不等式的解的公共部分,叫做一元一次不等式组的解.实质:公共部分注意:并非一定有公共部分,如果没有不等式组无解对于 的实质什么?最后又怎样来更简捷地表达呢?· 直观性原则是教学的基本原则.利用数轴形象直观地说明公共部分,是笛卡儿数学创造的再现.这也是再创造最好的体现.
用数抽来说明不等式组的解,(数形结合思想方法)也成为解决问题的一条主线.
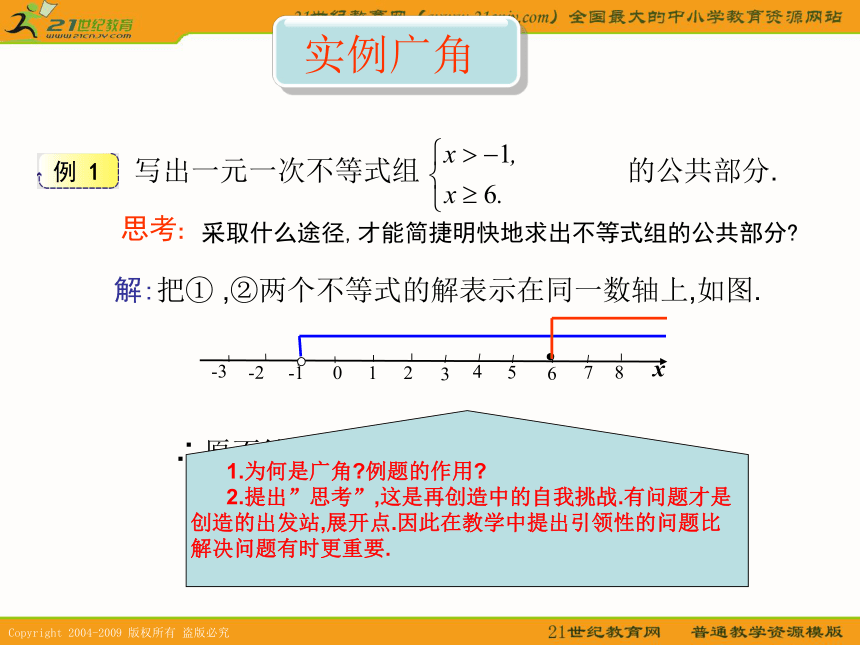
写出一元一次不等式组 的公共部分.∴原不等式组的公共部分是x≥6.解:把① ,②两个不等式的解表示在同一数轴上,如图. 1.为何是广角?例题的作用?
2.提出”思考”,这是再创造中的自我挑战.有问题才是
创造的出发站,展开点.因此在教学中提出引领性的问题比
解决问题有时更重要.思考:采取什么途径,才能简捷明快地求出不等式组的公共部分?★合作探究1.请分别改变每个不等式中不等号的方向,再编出三道题;
2. 利用类似于例1的方法分别求出改编的一元一次不等式组公共部分. 四人小组合作学习,选定代表汇报. 例题讨论完了,拓展例题,利用其资源价值,发散讨论,是再创造的有效途径.
这里巧妙地引导学生解决不等组解的其它几种情况.既是高认知的需要,也是高参与的需要.成果x≥6x<-1-1<x≤6无解显示成果,数形结合,突破难点,抓住关键.★快乐套餐二xx8-40-3-1-2x1.-3<x≤4x>2无解x≤ -1.5-5根据数轴上的表示,口答:及时反馈,让主线扎根于学生脑海.★快乐套餐三x>2x=2无解根据数轴上的表示,口答: 一般中蕴涵着特殊.在数学再创造中到处充满着这一数学的教
育哲理,只有理解这个哲理,数学学习的再创造就达到最严谨美的
魅力.x>n.x<m.m<x<n.无解若m<n,那么不等式组的解,有下列四种情况归纳提炼 1.有特殊到一般,这是一种归纳和类比方法的合情推理,适合初中生学习,也是新课程大力倡导的创造活动.
2.口诀问题所以原不等式组的整数解是1,2.把① ,②两个不等式的解表示在同一数轴上,如图. 1.注重解题的规范性,这是学习的需要,也是在创造成果的总结,是解决问题的要求.只有培养学生良好的学习习惯,才能更好的创造.
2.利用原例题拓展这是再创造的最佳时机.也是再创造的最好体现.
★快乐套餐四1.利用练习
及时反馈巩
固创造成果.
2.数学来于
生活,又回
归生活.★蓦然回首“一二三”课堂点金一二三,
简明扼要形成学生的认知框架,这是再创造的成果.如 解不等式组
三个步骤课本作业题. 配套作业本相应内容.让数学学习优秀学生脱颖而出.让创造的火花在他们身上不断闪现.一点补充: 高认知、高参与、高情意,简称“三高”,要十分注意:不要忽考高情意。只有努力改变教师的教育态度特质,走进学生的心灵世界,引导学生乐学,那么,我们的课堂教学就会真正的成功。
第三层:三维目标——三高
第二层:四大要素——支撑 第一层:五个环节——行为共12个切入点互相紧密联系。
“再创造”是一个举足轻重的现代课堂的要素。抓住这个点,并以五个环节为载体来反思自己的课堂教学。何谓再创造? 遵循数学本身发展和学生认知规律,引导学生在已有的生活经验上,通过师生活动,经历数学发现的过程拓展学生思维,从而实现数学学习目标的现代数学学习方式。三大特点 1.在教育的环境下创造,有别于数学家发现数学;
2.它可以是逻辑思维方法学习,也十分注重合情推理方法学习;
3.它可以是独立学习,也十分重视合作学习;
4.它是教师行为,也是学生行为.教师帮助学生自己帮助自己的学习.数学老师的体重大致在什么范围?信息1:设数学老师的体重为x千克,盛老师的体重小于小明体重(65千克)的2倍还少39.5千克.可列出不等式. 信息2:数学老师的体重的2倍不小于小明体重(65千克)的2倍还多50千克.可列出不等式. x<2×65-39.5, ①2x≥2×65+50. ②
★提出问题 1.单独的不等式①能比较好地确定老师的体重范围吗? 2.单独的不等式②能比较好地确定老师的体重范围吗?3.怎样才能较好地确定老师的体重范围呢?x满足不等式①,且满足不等式②——用大括号组合两个不等式.x<90.5.x≥90.0.建立这个教学环节在于提出问题,引入课题.这个环节,教师舍去了教材提供的引入题.理由是 1.远离学生生活实际的“公司购买商品”,没有很好的联系学生的生活经验;
2.直接给出了不等式组,等于是一种灌输,起不到不等式组产生的实际需要的必然性;
3.无法围绕本课主题内容,让学生带着最本质的问题去学习. 一句话,教材给出的,是数学本身的数学,但不是有利于学生学习创造的数学.而本人在这方面正好弥补了教材的缺陷.(强调要用教材)关于课堂情景的创设(寻求知识固定点)
趣——激发兴趣
疑——问题意识
明——明确主题反思:★观察思考 不等式① ②组合在一起,具有什么特征?
·· (2)两个不等式都是一元一次不等式.(1)含有同一个未知数x;定义一:至少有两个含有同一个未知数的一元一次不等式组成的一组不等式,叫做一元一次不等式组.1.这部分最能体现在创造的价值.观察思考其特点,不是现在的描述性定义让学生去死记.这是再创造的最初要义.
2.创造往往从观察开始,初步认识一元一次不等式组的内涵特征.
3.虽然强调概念内涵特征.但课程标准没有明确对定义的了解,更没有理解的要求.这里能这样点到得出定义就可以了.(熟练解不等式组才是重点)
★活动体验 某校即将举行校庆,一批知名校友将来母校参加典礼活动,需要我班几名女同学做礼仪服务,在身高上有要求.基本条件一:身高要不低于1.60米女同学,基本条件二:身高要低于1.65米女同学. 谁能有机会成为礼仪服务员,为学校做一点微薄的贡献呢?x ≥ 1.60请站起来.身高x满足请站起来.身高x满足x<1.65两次都站起来过的学生再站起来亮相.她们身高x满足再创造除了抽象理性的探究,也要十分重视学生的具体感性体验.
求公共部分是这个内容的难点,也是关键.通过身边的活动的体验性学习,不仅让学生乐于学习,也培养了学生在活动中,去发现问题去认识问题-------不等式组的解其实就是求每一个不等式的公共部分. 1.60≤x<1.65.定义二:组成不等式组的各个不等式的解的公共部分,叫做一元一次不等式组的解.实质:公共部分注意:并非一定有公共部分,如果没有不等式组无解对于 的实质什么?最后又怎样来更简捷地表达呢?· 直观性原则是教学的基本原则.利用数轴形象直观地说明公共部分,是笛卡儿数学创造的再现.这也是再创造最好的体现.
用数抽来说明不等式组的解,(数形结合思想方法)也成为解决问题的一条主线.
写出一元一次不等式组 的公共部分.∴原不等式组的公共部分是x≥6.解:把① ,②两个不等式的解表示在同一数轴上,如图. 1.为何是广角?例题的作用?
2.提出”思考”,这是再创造中的自我挑战.有问题才是
创造的出发站,展开点.因此在教学中提出引领性的问题比
解决问题有时更重要.思考:采取什么途径,才能简捷明快地求出不等式组的公共部分?★合作探究1.请分别改变每个不等式中不等号的方向,再编出三道题;
2. 利用类似于例1的方法分别求出改编的一元一次不等式组公共部分. 四人小组合作学习,选定代表汇报. 例题讨论完了,拓展例题,利用其资源价值,发散讨论,是再创造的有效途径.
这里巧妙地引导学生解决不等组解的其它几种情况.既是高认知的需要,也是高参与的需要.成果x≥6x<-1-1<x≤6无解显示成果,数形结合,突破难点,抓住关键.★快乐套餐二xx8-40-3-1-2x1.-3<x≤4x>2无解x≤ -1.5-5根据数轴上的表示,口答:及时反馈,让主线扎根于学生脑海.★快乐套餐三x>2x=2无解根据数轴上的表示,口答: 一般中蕴涵着特殊.在数学再创造中到处充满着这一数学的教
育哲理,只有理解这个哲理,数学学习的再创造就达到最严谨美的
魅力.x>n.x<m.m<x<n.无解若m<n,那么不等式组的解,有下列四种情况归纳提炼 1.有特殊到一般,这是一种归纳和类比方法的合情推理,适合初中生学习,也是新课程大力倡导的创造活动.
2.口诀问题所以原不等式组的整数解是1,2.把① ,②两个不等式的解表示在同一数轴上,如图. 1.注重解题的规范性,这是学习的需要,也是在创造成果的总结,是解决问题的要求.只有培养学生良好的学习习惯,才能更好的创造.
2.利用原例题拓展这是再创造的最佳时机.也是再创造的最好体现.
★快乐套餐四1.利用练习
及时反馈巩
固创造成果.
2.数学来于
生活,又回
归生活.★蓦然回首“一二三”课堂点金一二三,
简明扼要形成学生的认知框架,这是再创造的成果.如 解不等式组
三个步骤课本作业题. 配套作业本相应内容.让数学学习优秀学生脱颖而出.让创造的火花在他们身上不断闪现.一点补充: 高认知、高参与、高情意,简称“三高”,要十分注意:不要忽考高情意。只有努力改变教师的教育态度特质,走进学生的心灵世界,引导学生乐学,那么,我们的课堂教学就会真正的成功。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
