八年级数学下册浙教版 3.3《方差和标准差》小节复习题(含解析)
文档属性
| 名称 | 八年级数学下册浙教版 3.3《方差和标准差》小节复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 536.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 00:00:00 | ||
图片预览




文档简介
3.3《方差和标准差》小节复习题
题型01 求方差
1.一组数据2、4、4、6中加入数字4,组成一组新的数据,对比前后两组数据,变化的是( )
A.平均数 B.中位数 C.众数 D.方差
2.某社团统计成员一周的活动时间情况,列出了方差的计算公式:,则的值是( )
A.1 B.5 C. D.
3.一组数据,,,,的平均数是,则这组数据的中位数是 ,方差是 .
4.某学校在第三次数学学科评价5组的数学成绩是106,109,110,111,114;8组的数成绩是105,107,109,110,119,则这两个小组本次学科评价中数学成绩波动小的一组是 组
(方差公式 )
5.“共抗疫情,爱国力行”,为加强抗击疫情的爱国主义教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为分)如图所示.
(1)请你计算两个班的平均成绩各是多少分;
(2)直接写出两个班竞赛成绩的中位数,八年级(1)班______,八年级(2)班______;
(3)请结合两班竞赛成绩的平均数和中位数,你认为 个班的竞赛成绩较好;
(4)计算两个班竞赛成绩的方差,八年级(1)方差为______,八年级(2)方差为______,并说明______班的成绩较为整齐.
题型02 利用方差求未知数据的值
1.若一组数据2,3,4,的方差比另一组数据5,6,7,8的方差大,则的值可能是( )
A.1 B.3 C.5 D.7
2.若一组数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x不可以是( )
A.10 B.8 C.6 D.4
3.在对一组样本数据进行分析时,小明列出了计算方差的式子:,则 .
4.在方差计算公式,若,分别表示这组数据的个数和平均数,则的值为 .
5.某校为加强学生消防安全教育,要了解全校共1200名同学对消防知识的掌握情况,对他们进行了消防知识测试.现随机抽取甲,乙两班各15名同学的测试成绩进行整理分析,过程如下:
【收集数据】
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100.
乙班15名学生测试成绩分别为:
81,82,83,85,87,96,87,92,94,95,87,93,95,96,97.
【分析数据】
班级 平均数 众数 中位数 方差
甲 92 100 a
乙 90 b 91
【应用数据】
(1)根据以上信息,可以求出:_____分,______分;
(2)在计算这两组数据的方差时用的公式是,其中在计算乙班这组数据的方差时,公式中的______,______;
(3)结合以上数据,利用平均数或方差对两个班的成绩进行分析.
题型03 根据方差判断稳定性
1.为筹备班级联欢会,班长对全班学生爱吃的水果进行了民意调查,那么最终买什么水果,下面的数据最值得关注的是( )
A.众数 B.中位数 C.平均数 D.方差
2.甲、乙、丙、丁四位同学在四次数学测验中成绩的平均数相同,方差分别为,,,,则成绩最稳定的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
3.甲、乙、丙、丁四名同学进行1000米测试,每人5次测试成绩的平均数都是4分05秒,方差分别为,则这四名同学1000米成绩最稳定的是 .
4.甲、乙两位同学在五次数学测试中,平均成绩均为分,方差分别为,,甲、乙两位同学中成绩较稳定的是 同学.
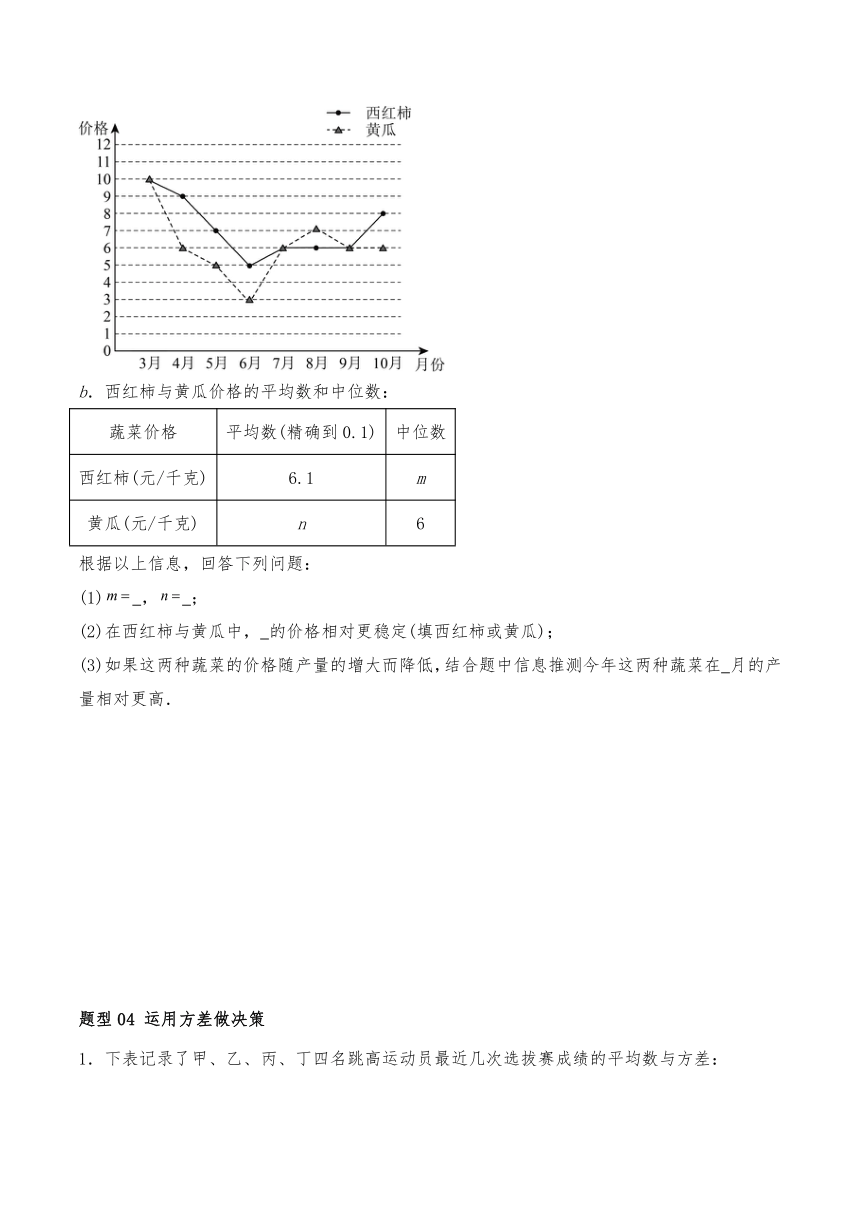
5.某小组去年3月至10月对当地西红柿与黄瓜市场价格进行调研,经过整理、描述和分析得到了部分信息.
a.西红柿与黄瓜市场价格的折线图:
b.西红柿与黄瓜价格的平均数和中位数:
蔬菜价格 平均数(精确到0.1) 中位数
西红柿(元/千克) 6.1 m
黄瓜(元/千克) n 6
根据以上信息,回答下列问题:
(1) , ;
(2)在西红柿与黄瓜中, 的价格相对更稳定(填西红柿或黄瓜);
(3)如果这两种蔬菜的价格随产量的增大而降低,结合题中信息推测今年这两种蔬菜在 月的产量相对更高.
题型04 运用方差做决策
1.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数 180 185 185 180
方差
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
2.下表记录了甲、乙、丙、丁四名运动员选拔赛成绩的平均数与方差S2.根据表中数据,要从中选择一名成绩好,又发挥稳定的运动员参加比赛,应该选择( )
甲 乙 丙 丁
平均数/ 561 560 561 560
方差 15.5 3.5 3.5 15.6
A.甲 B.乙 C.丙 D.丁
3.果农随机从甲、乙、丙三个品种的枇杷树中各选棵,每棵产量的平均数(单位:千克)及方差(单位:千克)如下表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是 .
甲 乙 丙
4.新郑红枣又名鸡心枣,是河南省郑州市新郑市的特产,素有“灵宝苹果潼关梨,新郑大枣甜似蜜”的盛赞.某外贸公司从甲、乙两个红枣厂家各随机抽取15盒进行检测,平均质量都是200克/盒,方差分别是,,你认为外贸公司会选择 红枣厂家.(填“甲”或“乙”).
5.为让学生了解广西的历史、地理等方面的知识,增强文化教育,某校组织学生进行“壮美家乡知多少”知识竞赛,满分分,学生得分均为整数.在初赛中,甲、乙两组每组人学生成绩如下单位:分:
甲组:,,,,,,,,,
乙组:,,,,,,,,,
组别 平均数 中位数 众数 方差
甲组 3.76
乙组 1.16
(1)以上成绩统计分析表中_______,_______,_______;
(2)小明同学说:“这次竞赛我得了7分,在我们小组中属中游略偏上!”观察上面表格判断,小明可能是_______组的学生;
(3)从平均数和方差看,若从甲、乙两组学生中选择一个组参加决赛,应选哪个组?并说明理由.
题型05 求极差
1.某学习小组的5名同学在一次数学文化节竞赛活动中的成绩(单位:分)分别是92,96,90,92,85,则下列结论不正确的是( )
A.中位数是92 B.众数是92 C.平均数是91 D.极差是7
2.成都市某一周内每天的最高气温为:(单位:),则这组数据的极差为( )
A.2 B.4 C.6 D.8
3.东海某日天气预报显示最高气温为,最低气温为,则该日的气温极差为 .
4.某学习小组共20人,他们的一次数学考试成绩如下表:
分数 60 70 79 80 85 90 95 100
人数 1 1 2 5 2 7 1 1
这20人成绩的中位数是 分,众数是 分,极差是 分.
5.为强化防溺水安全教育,提高学生安全意识和自我保护能力.某校组织了“珍爱生命,预防溺水”安全知识竞赛,满分100分.以下是从七、八年级各随机抽取10名学生的成绩进行统计,过程如下:
[收集数据]
七年级:99,95,95,91,100,86,77,93,85,79
八年级:99,91,97,63,96,97,100,94,87,76
[整理数据]
年级
七年级 0 2 6
八年级 1 1 1 7
[分析数据]
年级 平均数 众数 中位数 极差
七年级 90 95 b 23
八年级 90 c 95 d
[应用数据]
(1)由上表填空:______,______,______,______;
(2)你认为哪个年级的学生对防溺水安全知识了解水平较高?请说明理由.
题型06 已知极差求未知数据
1.如果一组数据,0,3,5,的极差是9,那么x的值( )
A.9 B.7 C. D.7或
2.若一组数据,0,2,5,x的极差为8,则x的值是( ).
A. B.8或 C.8 D.7或
3.已知一个样本有50个数据,其中最大值为83,最小值为32,若取组距为10,则应把它分成 组.
4.若五个数据2,,3,x,5的极差为8,则x的值为 .
5.如果一组数据1,3,5,x的极差为6,求这组数据的平均数.
题型07 标准差
1.已知样本数据,下列说法不正确的是( )
A.平均数是3 B.方差是2 C.中位数是4 D.标准差是
2.甲、乙、丙、丁四名射击运动员参加射击预选赛,每人射击20发子弹.他们射击成绩的平均数及标准差如下表所示:
人员成绩 甲 乙 丙 丁
平均数(环) 8.7 8.7 9.1 9.1
标准差(环) 1.3 1.5 1.0 1.2
若要选一名成绩较好且发挥稳定的运动员参奏,则应选择( )
A.甲 B.乙 C.丙 D.丁
3.已知四个数据的方差是,那么四个数据的标准差是 .
4.已知一个样本1、a、3、4、7,它的平均数是4,则这个样本的标准差是 .
5.(1)若一组数据…,的方差是9,则数据,…,的方差是多少?
(2)若一组数据…,的方差为,将这组数据中的每个数乘以9,则所得到的一组新数据的标准差是多少?
(3)若一组数据…,的方差为,将这组数据中的每个数乘以a,再加上b,那么得到的一组新数据的方差是多少?标准差是多少?
参考答案
题型01 求方差
1.D
【分析】根据平均数的定义:一组数据的总和除以这组数据的个数所得的商,叫做这组数据的算术平均数,简称平均数;众数的定义:一组数据中出现次数最多的数据;中位数的定义:一组数据中,处在最中间或处在最中间的两个数的平均数;方差的定义:一组数据中各个数据与它们平均数的差的平方的和的平均数,进行求解即可.
【详解】解:由题意得:原来的平均数为,
加入数字4之后的平均数为,
∴平均数没有发生变化,故A选项不符合题意;
原数据处在最中间的两个数为4和4,
∴原数据的中位数为4,
把新数据从小到大排列为2、4、4、4、6,处在最中间的数是4,
∴新数据的中位数为4,
∴中位数没有发生变化,故B选项不符合题意;
原数据中4出现的次数最多,
∴原数据的众数为4,
新数据中4出现的次数最多,
∴新数据的众数为4,
∴众数没有发生变化,故C选项不符合题意;
原数据的方差为,
新数据的方差为,
∴方差发生了变化,故D选项符合题意;
故选D.
2.D
【分析】本题主要考查方差的定义及加权平均数的计算公式,解题的关键是掌握方差的计算公式及公式中各个符号的含义.
【详解】解:由题意知,这组数据为、、、、、、、、、,
∴这组数据的的平均数为,
故选D.
3. 5
【分析】本题考查了已知平均数求数据中的未知数、求方差以及中位数,先求出的值,再根据中位数的定义:把数值排序后取中间位置的数;结合方差公式代入数值进行计算,据此即可作答.
【详解】解:,
这组数据为,,,,,
故中位数为.
,
故答案为:,.
4.5
【分析】本题考查了算术平均数、方差,先分别计算两组的平均数,然后利用方差公式计算两组的方差即可.
【详解】解:5组的平均数为,
8组的平均数为,
5组的方差为,
8组的方差为,
∵,
∴波动小的一组是5组.
故答案为:5.
5.(1)解:由题意可得,
八(1)班的平均数为:,
八(2)班的平均数为:,
∴八年(1)班平均成绩是分,八年(2)班平均成绩是分;
(2)解:由题意可得,
八(1)班的数据为:,八(2)班的数据为:,
∴八(1)班的中位数为:,八(2)班的中位数为:,
故答案为:分,分;
(3)解:∵两班的平均数相同,八(1)的中位数低于八(2)班的中位数,
∴八(2)班的竞赛成绩较好;
(4)解:由题意可得,
八(1)班的方差为:,
八(2)班的方差为:,
∵,
∴八年级(1)班的成绩较为整齐,
故答案为:,,八年级(1).
题型02 利用方差求未知数据的值
1.D
【分析】本题主要考查方差,解题的关键是掌握方差的定义和方差的意义.观察两组数据分布特点,根据方差的意义求解,也可先计算出后一组数据的方差,再取一个x的值计算出前一组数据的方差求解.
【详解】解:数据5,6,7,8,每2个数相差1;数据2,3,4, x的前3个数据也相差1,若或,两组数据方差相等,
而数据2,3,4,的方差比另一组数5,6,7,8的方差大,说明2,3,4,的波动大,则x的值可能是7,
故D正确.
故选D.
2.A
【分析】本题主要考查方差,观察两组数据分布特点,根据方差表示的是数据波动大小求解.
【详解】数据11、13、15、17、19中,相邻两个数相差为2,一组数据1,3,5,7,前4个数据也是相差2,数据波动一致,
∴若或时,两组数据方差相等,
当时1,3,5,7,的数据波动比11、13、15、17、19小,即方差更小,
当或时1,3,5,7,的数据波动比11、13、15、17、19大,即方差更大,
则的值不可能是10.
故选:A.
3.5
【分析】本题考查方差和平均数的应用,解题的关键是根据方差的定义得出这组数据.
根据公式找出这组数据、平均数,根据平均数公式计算出x即可.
【详解】
这组数据为:3,5,x,4,3,平均数为:4,
,
故答案为:5
4.
【分析】本题考查了方差的公式,理解公式的意义是解题的关键.
【详解】方差计算公式,,分别表示这组数据的个数和平均数,
∴,
∴,
故答案为:.
5.(1)解:把甲班15名学生测试成绩从小到大排列为
78,83,85,87,89,90,92,93,97,94,95,98,99,100,100,
位于正中间的数为93分,
∴,
乙班15名学生测试成绩中87分的人数最多,
∴乙班的众数,
故答案为:93,87;
(2)解:根据题意得:,;
故答案为:15,90;
(3)解:从平均分看,甲班成绩的平均数大于乙班,
所以甲班整体平均成绩大于乙班;
从方差看,甲班成绩的方差大于乙班,
所以乙班成绩更稳定.
题型03 根据方差判断稳定性
1.A
【分析】根据平均数、中位数、众数、方差的意义进行分析选择.
【详解】平均数、中位数、众数是描述一组数据集中程度的统计量;方差、标准差是描述一组数据离散程度的统计量.既然是为筹备班级联欢会做准备,那么买的水果肯定是大多数人爱吃的才行,故最值得关注的是众数.
故选A.
2.D
【分析】本题考查了方差的意义,根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】解:∵,,,,,
∴
∴成绩最稳定的是丁同学,
故选:D.
3.丁
【分析】本题主要考查了方差与稳定性之间的关系,熟知方差越小成绩越稳定是解题的关键.
【详解】解:∵,
∴方差最小的为丁,
∴这四名同学1000米成绩最稳定的是丁.
故答案为:丁.
4.甲
【分析】本题主要考查了方差,方差是衡量一组数据稳定程度的一个度量,方差越小,其数据越稳定.两组数据进行比较,方差小的一组更稳定.
【详解】解:,,,
,
甲同学的成绩较稳定,
故答案为:甲.
5.(1)解:把西红柿的价格从小到大排列,排在中间的两个数分别是6和7,故中位数;
;
故答案为:6.5;7.0;
(2)解:由折线统计图可知,西红柿的价格在5元/千克至10元/千克徘徊,黄瓜的价格在3元/千克至10元/千克徘徊,所以在西红柿与黄瓜中,西红柿的价格相对更稳定.
故答案为:西红柿;
(3)解:由统计图可知,6月份两种蔬菜的价格最低,所以如果这两种蔬菜的价格随产量的增大而降低,结合题中信息推测这两种蔬菜在6月的产量相对更高.
故答案为:6.
题型04 运用方差做决策
1.B
【分析】本题考查用平均数和方差做决策,正确理解方差与平均数的意义是解题关键.先比较平均数,再比较方差,平均数相同时选择方差较小的运动员参加即可.
【详解】解:∵且,
∴乙的平均数高且方差小发挥稳定性好,应该选择乙.
故选:B.
2.C
【分析】本题考查了平均数和方差的知识,掌握平均数和方差的意义即可解决问题.本题选择平均数大且方差小的即可.
【详解】因为队员乙和丙的方差最小,但队员乙平均数小,所以丙的成绩好,所以队员丙成绩好又发挥稳定.
故选:C.
3.甲
【分析】本题考查了方差和平均数,先比较平均数得到甲和乙产量较高,然后比较方差得到甲比较稳定,即可求解,掌握方差越小数据越稳定是解题的关键.
【详解】解:因为甲、乙的平均数比丙大,所以甲、乙的产量较高,又甲的方差比乙小,所以甲的产量比较稳定,
即从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是甲;
故答案为:甲.
4.乙
【分析】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,根据方差的意义可作出判断.
【详解】解:∵甲、乙两个红枣厂家各随机抽取15盒进行检测,平均质量都是200克/盒,方差分别是,,
,
∴较整齐的是乙厂,外贸公司会选择乙红枣厂家,
故答案为:乙.
5.(1)解:把甲组的成绩从小到大排列后,中间两个数的平均数是,则中位数;
,
乙组学生成绩中,数据7出现了四次,次数最多,所以众数.
故答案为:6;6.8;7;
(2)解:小明可能是甲组的学生,理由如下:
因为甲组的中位数是6分,而小明得了7分,所以在小组中属中游略偏上,
故答案为:甲;
(3)解:选乙组参加决赛.理由如下:
∵两组平均数相同,,
∴乙组的成绩比较稳定,
故选乙组参加决赛.
题型05 求极差
1.D
【分析】本题查了中位数、众数、平均数以及极差.直接根据中位数、众数、平均数以及极差的计算公式对各选项进行判断.
【详解】解:A.这组数据按从小到大排列为:85、90、92、92、96,所以这组数据的中位数是92,不符合题意;
B、这组数据的众数是92分,不符合题意;
C、这组数据的平均分是,不符合题意;
D、这组数据极差是,符合题意;
故选:D.
2.C
【分析】根据极差是最大值减去最小值进行计算即可.
【详解】解:;
故选C.
3.12
【分析】此题考查了极差,熟练掌握极差的定义是解题的关键.最大值与最小值的差叫做极差,根据极差定义进行求解即可.
【详解】解:,
该日的气温极差为,
故答案为:12.
4. 85 90 40
【分析】此题主要考查了中位数、众数以及极差的定义,正确把握相关定义是解题关键.直接利用中位数、众数以及极差的定义分别分析得出答案.
【详解】解:这组数据按从小到大排列,第10个和第11个数都是85分,所以这组数据的中位数为(分,
这组数据中90分最多有7个,所以众数是90(分,
极差是(分.
故答案为:85,90,40.
5.解:(1)由收集数据,可得七年级成绩为的学生人数有2人,
,
将七年级成绩从小到大排序为:77,79,85,86,91,93,95,95,99,100,
七年级成绩的中位数为:,
,
八年级的成绩为97的人数最多,即众数为97,
,
八年级的成绩最大值为,最小值为63,极差为:,
;
故答案为:2;92;97;37;
(2)八年级的学生对防溺水知识了解水平较高,理由如下:
从平均数看,两个年级的平均成绩相同;从中位数和众数来看,八年级的中位数和众数都高于七年级的中位数和众数;从极差来看,七年级的极差较八年级低;综合来看八年级的学生对防溺水知识了解水平较高.
题型06 已知极差求未知数据
1.D
【分析】根据极差的概念求解.
【详解】解:当为最大值时,,
解得:,
当为最小值时,,
解得:.
故选:D.
2.D
【分析】当x为最大值和最小值时分别根据极差列方程即可.
【详解】解:当x为最大值时,
,
解得;
当x为最小值时,
,
解得,
故选D.
3.6
【分析】先计算出该组数据的极差,根据组数极差组距即可求解.
【详解】解:最大值为83,最小值为32,
,
(组)(进一法取近似值),
故答案为:6.
4.7或
【分析】根据题目给的数据和极差的定义,可分两种情况讨论:x是最大值和x是最小值,分别列式计算,可求解.
【详解】解:由题意可得:极差是8,故x不可能是中间值,
若x是最大值,则,∴,
若x是最小值,则,∴,
则x的值为7或,
故答案为:7或.
5.解:一组数据1,3,5,x的极差是6,
当x为最大值时,x-1=6,则x=7,平均数是:(1+3+5+7)÷4=4;
当x是最小值时,5-x=6,解得:x=-1,平均数是:(-1+1+3+5)÷4=2.
故答案为:4或2.
题型07 标准差
1.C
【分析】根据平均数、方差、中位数和极差的定义逐项判断即得答案.
【详解】解:A、这组数据的平均数为,故本选项说法正确;
B、这组数据的方差是,故本选项说法正确;
C、这组数据的中位数是3,故本选项说法不正确;
D、这组数据的标准差是,故本选项说法正确;
故选:C.
2.C
【分析】先比较平均数,再比较标准差,然后得出丙的方差小于丁的方差,从而得出答案.
【详解】解:由图可知,丙和丁的平均成绩好,
∵丙的标准差小于丁的标准差,
∴丙的方差小于丁的方差,
∴若要选一名成绩较好且发挥稳定的运动员参奏,则应选择丙,
故选:C.
3.
【分析】本题考查了标准差,先求出四个数据的方差,再根据标准差是方差的算术平方根即可求解,掌握方差的计算公式是解题的关键.
【详解】解:设原数据的平均数为,新数据的每一个数都加了,则平均数变为,
则原数据的方差,
现在的方差,
,
∴数据的标准差为,
故答案为:.
4.
【分析】先由平均数的公式计算出a的值,根据方差的公式计算出方差,再计算标准差.
【详解】解:由题意得:
解得:
方差
∴标准差
故答案为:.
5.解:(1)设…,的平均数为,
则,…,的平均数为.
因为,
所以,…,的方差为
.
(2)设其平均数为a,则将每个数据都乘以9之后得到的新数分别为,…,,其平均数为,
所以原数据方差为
,
所以新数组,…,的标准差为.
(3)由(2)的结论可知这组数据中的每个数乘以a得到的新数组的方程为,
再根据(1)的结论可知将数据,…,中的每一个数都加上b以后得到的新数组与数组,…,的方差一样,仍为,
所以最后得到的新数组的标准差.
题型01 求方差
1.一组数据2、4、4、6中加入数字4,组成一组新的数据,对比前后两组数据,变化的是( )
A.平均数 B.中位数 C.众数 D.方差
2.某社团统计成员一周的活动时间情况,列出了方差的计算公式:,则的值是( )
A.1 B.5 C. D.
3.一组数据,,,,的平均数是,则这组数据的中位数是 ,方差是 .
4.某学校在第三次数学学科评价5组的数学成绩是106,109,110,111,114;8组的数成绩是105,107,109,110,119,则这两个小组本次学科评价中数学成绩波动小的一组是 组
(方差公式 )
5.“共抗疫情,爱国力行”,为加强抗击疫情的爱国主义教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为分)如图所示.
(1)请你计算两个班的平均成绩各是多少分;
(2)直接写出两个班竞赛成绩的中位数,八年级(1)班______,八年级(2)班______;
(3)请结合两班竞赛成绩的平均数和中位数,你认为 个班的竞赛成绩较好;
(4)计算两个班竞赛成绩的方差,八年级(1)方差为______,八年级(2)方差为______,并说明______班的成绩较为整齐.
题型02 利用方差求未知数据的值
1.若一组数据2,3,4,的方差比另一组数据5,6,7,8的方差大,则的值可能是( )
A.1 B.3 C.5 D.7
2.若一组数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x不可以是( )
A.10 B.8 C.6 D.4
3.在对一组样本数据进行分析时,小明列出了计算方差的式子:,则 .
4.在方差计算公式,若,分别表示这组数据的个数和平均数,则的值为 .
5.某校为加强学生消防安全教育,要了解全校共1200名同学对消防知识的掌握情况,对他们进行了消防知识测试.现随机抽取甲,乙两班各15名同学的测试成绩进行整理分析,过程如下:
【收集数据】
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100.
乙班15名学生测试成绩分别为:
81,82,83,85,87,96,87,92,94,95,87,93,95,96,97.
【分析数据】
班级 平均数 众数 中位数 方差
甲 92 100 a
乙 90 b 91
【应用数据】
(1)根据以上信息,可以求出:_____分,______分;
(2)在计算这两组数据的方差时用的公式是,其中在计算乙班这组数据的方差时,公式中的______,______;
(3)结合以上数据,利用平均数或方差对两个班的成绩进行分析.
题型03 根据方差判断稳定性
1.为筹备班级联欢会,班长对全班学生爱吃的水果进行了民意调查,那么最终买什么水果,下面的数据最值得关注的是( )
A.众数 B.中位数 C.平均数 D.方差
2.甲、乙、丙、丁四位同学在四次数学测验中成绩的平均数相同,方差分别为,,,,则成绩最稳定的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
3.甲、乙、丙、丁四名同学进行1000米测试,每人5次测试成绩的平均数都是4分05秒,方差分别为,则这四名同学1000米成绩最稳定的是 .
4.甲、乙两位同学在五次数学测试中,平均成绩均为分,方差分别为,,甲、乙两位同学中成绩较稳定的是 同学.
5.某小组去年3月至10月对当地西红柿与黄瓜市场价格进行调研,经过整理、描述和分析得到了部分信息.
a.西红柿与黄瓜市场价格的折线图:
b.西红柿与黄瓜价格的平均数和中位数:
蔬菜价格 平均数(精确到0.1) 中位数
西红柿(元/千克) 6.1 m
黄瓜(元/千克) n 6
根据以上信息,回答下列问题:
(1) , ;
(2)在西红柿与黄瓜中, 的价格相对更稳定(填西红柿或黄瓜);
(3)如果这两种蔬菜的价格随产量的增大而降低,结合题中信息推测今年这两种蔬菜在 月的产量相对更高.
题型04 运用方差做决策
1.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数 180 185 185 180
方差
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
2.下表记录了甲、乙、丙、丁四名运动员选拔赛成绩的平均数与方差S2.根据表中数据,要从中选择一名成绩好,又发挥稳定的运动员参加比赛,应该选择( )
甲 乙 丙 丁
平均数/ 561 560 561 560
方差 15.5 3.5 3.5 15.6
A.甲 B.乙 C.丙 D.丁
3.果农随机从甲、乙、丙三个品种的枇杷树中各选棵,每棵产量的平均数(单位:千克)及方差(单位:千克)如下表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是 .
甲 乙 丙
4.新郑红枣又名鸡心枣,是河南省郑州市新郑市的特产,素有“灵宝苹果潼关梨,新郑大枣甜似蜜”的盛赞.某外贸公司从甲、乙两个红枣厂家各随机抽取15盒进行检测,平均质量都是200克/盒,方差分别是,,你认为外贸公司会选择 红枣厂家.(填“甲”或“乙”).
5.为让学生了解广西的历史、地理等方面的知识,增强文化教育,某校组织学生进行“壮美家乡知多少”知识竞赛,满分分,学生得分均为整数.在初赛中,甲、乙两组每组人学生成绩如下单位:分:
甲组:,,,,,,,,,
乙组:,,,,,,,,,
组别 平均数 中位数 众数 方差
甲组 3.76
乙组 1.16
(1)以上成绩统计分析表中_______,_______,_______;
(2)小明同学说:“这次竞赛我得了7分,在我们小组中属中游略偏上!”观察上面表格判断,小明可能是_______组的学生;
(3)从平均数和方差看,若从甲、乙两组学生中选择一个组参加决赛,应选哪个组?并说明理由.
题型05 求极差
1.某学习小组的5名同学在一次数学文化节竞赛活动中的成绩(单位:分)分别是92,96,90,92,85,则下列结论不正确的是( )
A.中位数是92 B.众数是92 C.平均数是91 D.极差是7
2.成都市某一周内每天的最高气温为:(单位:),则这组数据的极差为( )
A.2 B.4 C.6 D.8
3.东海某日天气预报显示最高气温为,最低气温为,则该日的气温极差为 .
4.某学习小组共20人,他们的一次数学考试成绩如下表:
分数 60 70 79 80 85 90 95 100
人数 1 1 2 5 2 7 1 1
这20人成绩的中位数是 分,众数是 分,极差是 分.
5.为强化防溺水安全教育,提高学生安全意识和自我保护能力.某校组织了“珍爱生命,预防溺水”安全知识竞赛,满分100分.以下是从七、八年级各随机抽取10名学生的成绩进行统计,过程如下:
[收集数据]
七年级:99,95,95,91,100,86,77,93,85,79
八年级:99,91,97,63,96,97,100,94,87,76
[整理数据]
年级
七年级 0 2 6
八年级 1 1 1 7
[分析数据]
年级 平均数 众数 中位数 极差
七年级 90 95 b 23
八年级 90 c 95 d
[应用数据]
(1)由上表填空:______,______,______,______;
(2)你认为哪个年级的学生对防溺水安全知识了解水平较高?请说明理由.
题型06 已知极差求未知数据
1.如果一组数据,0,3,5,的极差是9,那么x的值( )
A.9 B.7 C. D.7或
2.若一组数据,0,2,5,x的极差为8,则x的值是( ).
A. B.8或 C.8 D.7或
3.已知一个样本有50个数据,其中最大值为83,最小值为32,若取组距为10,则应把它分成 组.
4.若五个数据2,,3,x,5的极差为8,则x的值为 .
5.如果一组数据1,3,5,x的极差为6,求这组数据的平均数.
题型07 标准差
1.已知样本数据,下列说法不正确的是( )
A.平均数是3 B.方差是2 C.中位数是4 D.标准差是
2.甲、乙、丙、丁四名射击运动员参加射击预选赛,每人射击20发子弹.他们射击成绩的平均数及标准差如下表所示:
人员成绩 甲 乙 丙 丁
平均数(环) 8.7 8.7 9.1 9.1
标准差(环) 1.3 1.5 1.0 1.2
若要选一名成绩较好且发挥稳定的运动员参奏,则应选择( )
A.甲 B.乙 C.丙 D.丁
3.已知四个数据的方差是,那么四个数据的标准差是 .
4.已知一个样本1、a、3、4、7,它的平均数是4,则这个样本的标准差是 .
5.(1)若一组数据…,的方差是9,则数据,…,的方差是多少?
(2)若一组数据…,的方差为,将这组数据中的每个数乘以9,则所得到的一组新数据的标准差是多少?
(3)若一组数据…,的方差为,将这组数据中的每个数乘以a,再加上b,那么得到的一组新数据的方差是多少?标准差是多少?
参考答案
题型01 求方差
1.D
【分析】根据平均数的定义:一组数据的总和除以这组数据的个数所得的商,叫做这组数据的算术平均数,简称平均数;众数的定义:一组数据中出现次数最多的数据;中位数的定义:一组数据中,处在最中间或处在最中间的两个数的平均数;方差的定义:一组数据中各个数据与它们平均数的差的平方的和的平均数,进行求解即可.
【详解】解:由题意得:原来的平均数为,
加入数字4之后的平均数为,
∴平均数没有发生变化,故A选项不符合题意;
原数据处在最中间的两个数为4和4,
∴原数据的中位数为4,
把新数据从小到大排列为2、4、4、4、6,处在最中间的数是4,
∴新数据的中位数为4,
∴中位数没有发生变化,故B选项不符合题意;
原数据中4出现的次数最多,
∴原数据的众数为4,
新数据中4出现的次数最多,
∴新数据的众数为4,
∴众数没有发生变化,故C选项不符合题意;
原数据的方差为,
新数据的方差为,
∴方差发生了变化,故D选项符合题意;
故选D.
2.D
【分析】本题主要考查方差的定义及加权平均数的计算公式,解题的关键是掌握方差的计算公式及公式中各个符号的含义.
【详解】解:由题意知,这组数据为、、、、、、、、、,
∴这组数据的的平均数为,
故选D.
3. 5
【分析】本题考查了已知平均数求数据中的未知数、求方差以及中位数,先求出的值,再根据中位数的定义:把数值排序后取中间位置的数;结合方差公式代入数值进行计算,据此即可作答.
【详解】解:,
这组数据为,,,,,
故中位数为.
,
故答案为:,.
4.5
【分析】本题考查了算术平均数、方差,先分别计算两组的平均数,然后利用方差公式计算两组的方差即可.
【详解】解:5组的平均数为,
8组的平均数为,
5组的方差为,
8组的方差为,
∵,
∴波动小的一组是5组.
故答案为:5.
5.(1)解:由题意可得,
八(1)班的平均数为:,
八(2)班的平均数为:,
∴八年(1)班平均成绩是分,八年(2)班平均成绩是分;
(2)解:由题意可得,
八(1)班的数据为:,八(2)班的数据为:,
∴八(1)班的中位数为:,八(2)班的中位数为:,
故答案为:分,分;
(3)解:∵两班的平均数相同,八(1)的中位数低于八(2)班的中位数,
∴八(2)班的竞赛成绩较好;
(4)解:由题意可得,
八(1)班的方差为:,
八(2)班的方差为:,
∵,
∴八年级(1)班的成绩较为整齐,
故答案为:,,八年级(1).
题型02 利用方差求未知数据的值
1.D
【分析】本题主要考查方差,解题的关键是掌握方差的定义和方差的意义.观察两组数据分布特点,根据方差的意义求解,也可先计算出后一组数据的方差,再取一个x的值计算出前一组数据的方差求解.
【详解】解:数据5,6,7,8,每2个数相差1;数据2,3,4, x的前3个数据也相差1,若或,两组数据方差相等,
而数据2,3,4,的方差比另一组数5,6,7,8的方差大,说明2,3,4,的波动大,则x的值可能是7,
故D正确.
故选D.
2.A
【分析】本题主要考查方差,观察两组数据分布特点,根据方差表示的是数据波动大小求解.
【详解】数据11、13、15、17、19中,相邻两个数相差为2,一组数据1,3,5,7,前4个数据也是相差2,数据波动一致,
∴若或时,两组数据方差相等,
当时1,3,5,7,的数据波动比11、13、15、17、19小,即方差更小,
当或时1,3,5,7,的数据波动比11、13、15、17、19大,即方差更大,
则的值不可能是10.
故选:A.
3.5
【分析】本题考查方差和平均数的应用,解题的关键是根据方差的定义得出这组数据.
根据公式找出这组数据、平均数,根据平均数公式计算出x即可.
【详解】
这组数据为:3,5,x,4,3,平均数为:4,
,
故答案为:5
4.
【分析】本题考查了方差的公式,理解公式的意义是解题的关键.
【详解】方差计算公式,,分别表示这组数据的个数和平均数,
∴,
∴,
故答案为:.
5.(1)解:把甲班15名学生测试成绩从小到大排列为
78,83,85,87,89,90,92,93,97,94,95,98,99,100,100,
位于正中间的数为93分,
∴,
乙班15名学生测试成绩中87分的人数最多,
∴乙班的众数,
故答案为:93,87;
(2)解:根据题意得:,;
故答案为:15,90;
(3)解:从平均分看,甲班成绩的平均数大于乙班,
所以甲班整体平均成绩大于乙班;
从方差看,甲班成绩的方差大于乙班,
所以乙班成绩更稳定.
题型03 根据方差判断稳定性
1.A
【分析】根据平均数、中位数、众数、方差的意义进行分析选择.
【详解】平均数、中位数、众数是描述一组数据集中程度的统计量;方差、标准差是描述一组数据离散程度的统计量.既然是为筹备班级联欢会做准备,那么买的水果肯定是大多数人爱吃的才行,故最值得关注的是众数.
故选A.
2.D
【分析】本题考查了方差的意义,根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】解:∵,,,,,
∴
∴成绩最稳定的是丁同学,
故选:D.
3.丁
【分析】本题主要考查了方差与稳定性之间的关系,熟知方差越小成绩越稳定是解题的关键.
【详解】解:∵,
∴方差最小的为丁,
∴这四名同学1000米成绩最稳定的是丁.
故答案为:丁.
4.甲
【分析】本题主要考查了方差,方差是衡量一组数据稳定程度的一个度量,方差越小,其数据越稳定.两组数据进行比较,方差小的一组更稳定.
【详解】解:,,,
,
甲同学的成绩较稳定,
故答案为:甲.
5.(1)解:把西红柿的价格从小到大排列,排在中间的两个数分别是6和7,故中位数;
;
故答案为:6.5;7.0;
(2)解:由折线统计图可知,西红柿的价格在5元/千克至10元/千克徘徊,黄瓜的价格在3元/千克至10元/千克徘徊,所以在西红柿与黄瓜中,西红柿的价格相对更稳定.
故答案为:西红柿;
(3)解:由统计图可知,6月份两种蔬菜的价格最低,所以如果这两种蔬菜的价格随产量的增大而降低,结合题中信息推测这两种蔬菜在6月的产量相对更高.
故答案为:6.
题型04 运用方差做决策
1.B
【分析】本题考查用平均数和方差做决策,正确理解方差与平均数的意义是解题关键.先比较平均数,再比较方差,平均数相同时选择方差较小的运动员参加即可.
【详解】解:∵且,
∴乙的平均数高且方差小发挥稳定性好,应该选择乙.
故选:B.
2.C
【分析】本题考查了平均数和方差的知识,掌握平均数和方差的意义即可解决问题.本题选择平均数大且方差小的即可.
【详解】因为队员乙和丙的方差最小,但队员乙平均数小,所以丙的成绩好,所以队员丙成绩好又发挥稳定.
故选:C.
3.甲
【分析】本题考查了方差和平均数,先比较平均数得到甲和乙产量较高,然后比较方差得到甲比较稳定,即可求解,掌握方差越小数据越稳定是解题的关键.
【详解】解:因为甲、乙的平均数比丙大,所以甲、乙的产量较高,又甲的方差比乙小,所以甲的产量比较稳定,
即从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是甲;
故答案为:甲.
4.乙
【分析】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,根据方差的意义可作出判断.
【详解】解:∵甲、乙两个红枣厂家各随机抽取15盒进行检测,平均质量都是200克/盒,方差分别是,,
,
∴较整齐的是乙厂,外贸公司会选择乙红枣厂家,
故答案为:乙.
5.(1)解:把甲组的成绩从小到大排列后,中间两个数的平均数是,则中位数;
,
乙组学生成绩中,数据7出现了四次,次数最多,所以众数.
故答案为:6;6.8;7;
(2)解:小明可能是甲组的学生,理由如下:
因为甲组的中位数是6分,而小明得了7分,所以在小组中属中游略偏上,
故答案为:甲;
(3)解:选乙组参加决赛.理由如下:
∵两组平均数相同,,
∴乙组的成绩比较稳定,
故选乙组参加决赛.
题型05 求极差
1.D
【分析】本题查了中位数、众数、平均数以及极差.直接根据中位数、众数、平均数以及极差的计算公式对各选项进行判断.
【详解】解:A.这组数据按从小到大排列为:85、90、92、92、96,所以这组数据的中位数是92,不符合题意;
B、这组数据的众数是92分,不符合题意;
C、这组数据的平均分是,不符合题意;
D、这组数据极差是,符合题意;
故选:D.
2.C
【分析】根据极差是最大值减去最小值进行计算即可.
【详解】解:;
故选C.
3.12
【分析】此题考查了极差,熟练掌握极差的定义是解题的关键.最大值与最小值的差叫做极差,根据极差定义进行求解即可.
【详解】解:,
该日的气温极差为,
故答案为:12.
4. 85 90 40
【分析】此题主要考查了中位数、众数以及极差的定义,正确把握相关定义是解题关键.直接利用中位数、众数以及极差的定义分别分析得出答案.
【详解】解:这组数据按从小到大排列,第10个和第11个数都是85分,所以这组数据的中位数为(分,
这组数据中90分最多有7个,所以众数是90(分,
极差是(分.
故答案为:85,90,40.
5.解:(1)由收集数据,可得七年级成绩为的学生人数有2人,
,
将七年级成绩从小到大排序为:77,79,85,86,91,93,95,95,99,100,
七年级成绩的中位数为:,
,
八年级的成绩为97的人数最多,即众数为97,
,
八年级的成绩最大值为,最小值为63,极差为:,
;
故答案为:2;92;97;37;
(2)八年级的学生对防溺水知识了解水平较高,理由如下:
从平均数看,两个年级的平均成绩相同;从中位数和众数来看,八年级的中位数和众数都高于七年级的中位数和众数;从极差来看,七年级的极差较八年级低;综合来看八年级的学生对防溺水知识了解水平较高.
题型06 已知极差求未知数据
1.D
【分析】根据极差的概念求解.
【详解】解:当为最大值时,,
解得:,
当为最小值时,,
解得:.
故选:D.
2.D
【分析】当x为最大值和最小值时分别根据极差列方程即可.
【详解】解:当x为最大值时,
,
解得;
当x为最小值时,
,
解得,
故选D.
3.6
【分析】先计算出该组数据的极差,根据组数极差组距即可求解.
【详解】解:最大值为83,最小值为32,
,
(组)(进一法取近似值),
故答案为:6.
4.7或
【分析】根据题目给的数据和极差的定义,可分两种情况讨论:x是最大值和x是最小值,分别列式计算,可求解.
【详解】解:由题意可得:极差是8,故x不可能是中间值,
若x是最大值,则,∴,
若x是最小值,则,∴,
则x的值为7或,
故答案为:7或.
5.解:一组数据1,3,5,x的极差是6,
当x为最大值时,x-1=6,则x=7,平均数是:(1+3+5+7)÷4=4;
当x是最小值时,5-x=6,解得:x=-1,平均数是:(-1+1+3+5)÷4=2.
故答案为:4或2.
题型07 标准差
1.C
【分析】根据平均数、方差、中位数和极差的定义逐项判断即得答案.
【详解】解:A、这组数据的平均数为,故本选项说法正确;
B、这组数据的方差是,故本选项说法正确;
C、这组数据的中位数是3,故本选项说法不正确;
D、这组数据的标准差是,故本选项说法正确;
故选:C.
2.C
【分析】先比较平均数,再比较标准差,然后得出丙的方差小于丁的方差,从而得出答案.
【详解】解:由图可知,丙和丁的平均成绩好,
∵丙的标准差小于丁的标准差,
∴丙的方差小于丁的方差,
∴若要选一名成绩较好且发挥稳定的运动员参奏,则应选择丙,
故选:C.
3.
【分析】本题考查了标准差,先求出四个数据的方差,再根据标准差是方差的算术平方根即可求解,掌握方差的计算公式是解题的关键.
【详解】解:设原数据的平均数为,新数据的每一个数都加了,则平均数变为,
则原数据的方差,
现在的方差,
,
∴数据的标准差为,
故答案为:.
4.
【分析】先由平均数的公式计算出a的值,根据方差的公式计算出方差,再计算标准差.
【详解】解:由题意得:
解得:
方差
∴标准差
故答案为:.
5.解:(1)设…,的平均数为,
则,…,的平均数为.
因为,
所以,…,的方差为
.
(2)设其平均数为a,则将每个数据都乘以9之后得到的新数分别为,…,,其平均数为,
所以原数据方差为
,
所以新数组,…,的标准差为.
(3)由(2)的结论可知这组数据中的每个数乘以a得到的新数组的方程为,
再根据(1)的结论可知将数据,…,中的每一个数都加上b以后得到的新数组与数组,…,的方差一样,仍为,
所以最后得到的新数组的标准差.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
