浙教版数学九年级下册 第1章 解直角三角形 单元测试(含答案)
文档属性
| 名称 | 浙教版数学九年级下册 第1章 解直角三角形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 23:21:25 | ||
图片预览


文档简介
浙教版九年级下 第1章 解直角三角形 单元测试
一.选择题(共12小题)
1.在Rt△ABC中,∠C=90°,AC=2,BC=1,则tan∠A的值为( )
A. B.2 C. D.
2.如图,在Rt△EFG中,∠F=90°,则tanE=( )
A. B. C. D.
3.4sin60°的值为( )
A.3 B.1 C. D.
4.如图,在Rt△ABC中,∠ACB=90°,CD垂直于,则BC=( )
A.7 B.8 C.9 D.10
5.在Rt△ABC中,∠C=90°,若cosA=,则tanA=( )
A.2 B. C. D.
6.在Rt△ABC中,已知∠C=90°,∠A=α,BC=a,那么AB的长为( )
A. B. C.asinα D.acosα
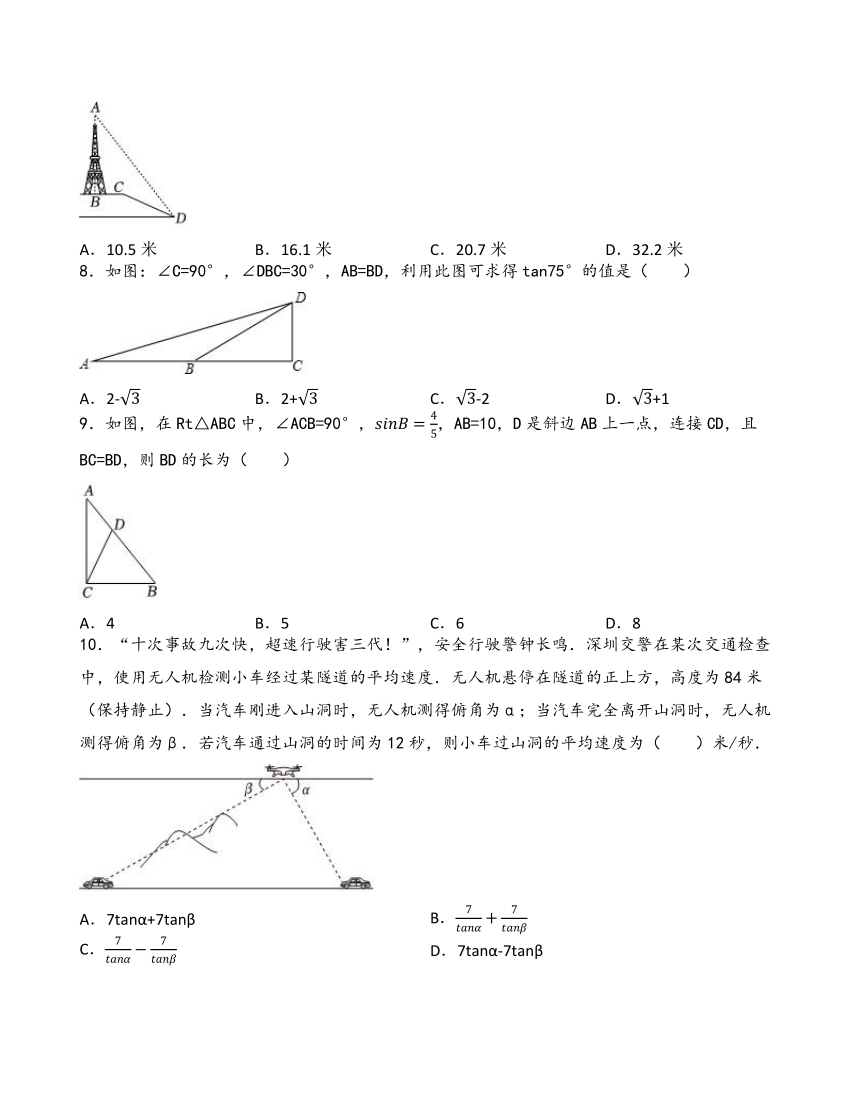
7.如图,为测量观光塔AB的高度,冬冬在坡度i=5:12的斜坡CD的D点测得塔顶A的仰角为52°,斜坡CD长为26米,C到塔底B的水平距离为9米.图中点A,B,C,D在同一平面内,则观光塔AB的高度约为( )米.(结果精确到0.1米,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)
A.10.5米 B.16.1米 C.20.7米 D.32.2米
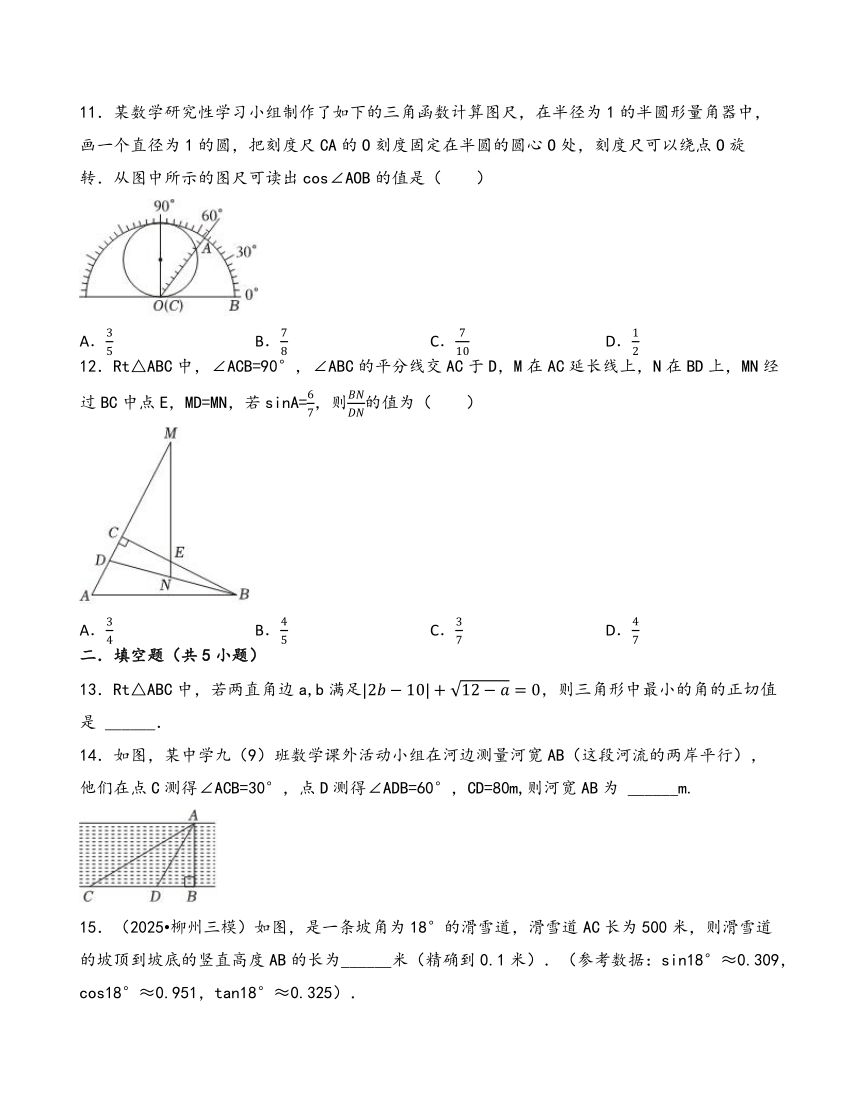
8.如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )
A.2- B.2+ C.-2 D.+1
9.如图,在Rt△ABC中,∠ACB=90°,,AB=10,D是斜边AB上一点,连接CD,且BC=BD,则BD的长为( )
A.4 B.5 C.6 D.8
10.“十次事故九次快,超速行驶害三代!”,安全行驶警钟长鸣.深圳交警在某次交通检查中,使用无人机检测小车经过某隧道的平均速度.无人机悬停在隧道的正上方,高度为84米(保持静止).当汽车刚进入山洞时,无人机测得俯角为α;当汽车完全离开山洞时,无人机测得俯角为β.若汽车通过山洞的时间为12秒,则小车过山洞的平均速度为( )米/秒.
A.7tanα+7tanβ B.
C. D.7tanα-7tanβ
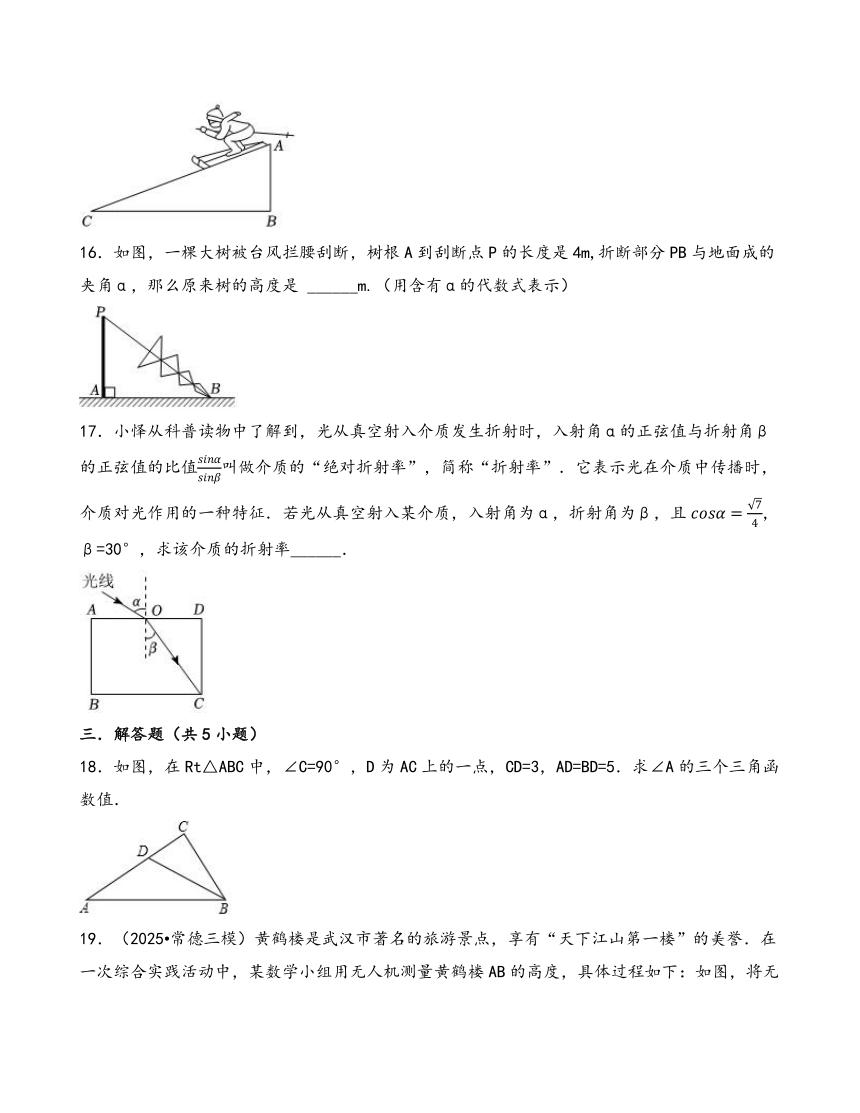
11.某数学研究性学习小组制作了如下的三角函数计算图尺,在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的O刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出cos∠AOB的值是( )
A. B. C. D.
12.Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于D,M在AC延长线上,N在BD上,MN经过BC中点E,MD=MN,若sinA=,则的值为( )
A. B. C. D.
二.填空题(共5小题)
13.Rt△ABC中,若两直角边a,b满足,则三角形中最小的角的正切值是 ______.
14.如图,某中学九(9)班数学课外活动小组在河边测量河宽AB(这段河流的两岸平行),他们在点C测得∠ACB=30°,点D测得∠ADB=60°,CD=80m,则河宽AB为 ______m.
15.(2025 柳州三模)如图,是一条坡角为18°的滑雪道,滑雪道AC长为500米,则滑雪道的坡顶到坡底的竖直高度AB的长为______米(精确到0.1米).(参考数据:sin18°≈0.309,cos18°≈0.951,tan18°≈0.325).
16.如图,一棵大树被台风拦腰刮断,树根A到刮断点P的长度是4m,折断部分PB与地面成的夹角α,那么原来树的高度是 ______m.(用含有α的代数式表示)
17.小怿从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.若光从真空射入某介质,入射角为α,折射角为β,且,β=30°,求该介质的折射率______.
三.解答题(共5小题)
18.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
19.(2025 常德三模)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB的高度,具体过程如下:如图,将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,求黄鹤楼的高度(参考数据:tan63°≈2).
20.(2025 三原县二模)如图,这是雨伞打开后的示意图,AP是伞柄,AB,AC是伞骨,=30cm,点D为伞圈,AP平分∠BAC,伞完全张开时∠BAC=120°.雨往往斜向落下,假设雨线之间是平行的.某一天,雨线BM与地面之间的夹角为60°,小伟站在伞圈点D正下方的点G处,将小伟的身高记为GH,此时他身上被雨淋湿,测得BN=150cm.求伞至少向下移动多少cm的距离,才能使得小伟站在点G处不被雨淋湿身上.
21.(2025 信都区二模)如图是嘉淇为某公司设计的公司标志示意图,四边形ABCD与四边形FECG是两个全等的平行四边形,点B、C、E在同一条直线上,点Q、N分别在边AD、GF上,且PM∥BE.已知点P到BC的距离为5,EF=5.56cm,∠DCG=30°.
(1)求点A到BC的距离;
(2)若PQ=4.64cm,试通过计算说明PQ∥CD.
[注:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73]
22.消防车是火灾消防救援的主要装备,确保人民生命财产安全.图1是某种消防车云梯,图2是其侧面示意图,点D,B,O在同一直线上,DO可绕着点O旋转,点O,A,C在同一水平线上,其中BD可伸缩,套管OB的长度不变,通过液压杆AB长度来调整∠DOC的大小,在某种工作状态下测得液压杆AB=°.
(1)求BO的长;
(2)消防人员在云梯末端点D高空作业时,将BD伸长到最大长度6m,再将云梯DO绕着点O顺时针旋转34°,此时云梯末端D的铅直高度升高了多少?(参考数据sin64°≈0.90,cos64°≈0.44)
浙教版九年级下 第1章 解直角三角形 单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、A 3、D 4、C 5、A 6、A 7、D 8、B 9、C 10、B 11、A 12、A
二.填空题(共5小题)
13、; 14、69; 15、154.5; 16、(4+); 17、;
三.解答题(共5小题)
18、解:在Rt△BCD中,∵CD=3、BD=5,
∴BC===4,
又AC=AD+CD=8,
∴AB===4,
则sinA===,
cosA===,
tanA===.
19、解:将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,如图,延长BA交距水平地面102m的水平线于点D,
依题意,有三个角都是直角的四边形是矩形,
∴BD=102m,
设AD=x cm,
∵∠DCA=45°,
∴DC=AD=x cm,
∴,
∴DC=AD≈51,
∴AB=BD-AD=102-51≈51(m),
∴黄鹤楼的高度约为51m.
20、解:如图,设AG与BC交于点O,与BM交于点Q.
∵∠BAC=120°,AP 平分∠BAC,
∴∠BAO=60°,
在Rt△ABO中,AB=3AE=90cm,∠BAO=60°,
∴BO=AB sin,
∴.
在Rt△BMN中,BN=150cm,∠BMN=60°,
∴.
在Rt△QGM中,.
答:伞至少向下移动15cm的距离,才能使得小伟站在点G处不被雨淋湿身上.
21、解:(1)过点A作AH⊥BC,垂足落在CB的延长线上,
∵四边形ABCD与四边形FECG是两个全等的平行四边形,
∴∠DCB=∠GCE,EF=AB,
∵∠DCG=30°,
∴∠DCB=75°.
∵AB∥CD,
∴∠ABH=∠DCB=75°,
∴AH=ABsin75°≈5.4(cm),
∴点A到BC的距离为5.4cm;
(2)过点P作PO⊥AD于O点,
∵点P到BC的距离为5,
∴PO=9.9-5.4=4.5,
∵,
∴∠PQO=75°.
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=75°,
∴∠PQO=∠DAB,
∴AB∥PQ,
∴PQ∥CD.
22、解:(1)如图1,过点B作BE⊥OC,垂足为E,
∵∠BAC=60°,∠DOC=30°,
∴∠ABO=∠DOC=30°,
∴OA=AB=m,
在Rt△AEB 中,BAC=60°,
∴∠ABE=30°,
∴AE=AB=,BE=AE=2,
在Rt△OEB 中,∠DOC=30°,
∴OB=2BE=4m;
(2)如图2,过点D作DN⊥OC,垂足为N,
在Rt△DNO中,OD=OB+BD=4+6=10,
∴DN=OD sin∠DON,
当∠DON=30°时,
DN=OD sin64°≈10×=5(m),
当∠DON=30°+34°=64°时,
DN=OD sin64°≈10×0.90=9(m),
9-5=4(米),
∴此时云梯末端D的铅直高度升高了4米.
一.选择题(共12小题)
1.在Rt△ABC中,∠C=90°,AC=2,BC=1,则tan∠A的值为( )
A. B.2 C. D.
2.如图,在Rt△EFG中,∠F=90°,则tanE=( )
A. B. C. D.
3.4sin60°的值为( )
A.3 B.1 C. D.
4.如图,在Rt△ABC中,∠ACB=90°,CD垂直于,则BC=( )
A.7 B.8 C.9 D.10
5.在Rt△ABC中,∠C=90°,若cosA=,则tanA=( )
A.2 B. C. D.
6.在Rt△ABC中,已知∠C=90°,∠A=α,BC=a,那么AB的长为( )
A. B. C.asinα D.acosα
7.如图,为测量观光塔AB的高度,冬冬在坡度i=5:12的斜坡CD的D点测得塔顶A的仰角为52°,斜坡CD长为26米,C到塔底B的水平距离为9米.图中点A,B,C,D在同一平面内,则观光塔AB的高度约为( )米.(结果精确到0.1米,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)
A.10.5米 B.16.1米 C.20.7米 D.32.2米
8.如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )
A.2- B.2+ C.-2 D.+1
9.如图,在Rt△ABC中,∠ACB=90°,,AB=10,D是斜边AB上一点,连接CD,且BC=BD,则BD的长为( )
A.4 B.5 C.6 D.8
10.“十次事故九次快,超速行驶害三代!”,安全行驶警钟长鸣.深圳交警在某次交通检查中,使用无人机检测小车经过某隧道的平均速度.无人机悬停在隧道的正上方,高度为84米(保持静止).当汽车刚进入山洞时,无人机测得俯角为α;当汽车完全离开山洞时,无人机测得俯角为β.若汽车通过山洞的时间为12秒,则小车过山洞的平均速度为( )米/秒.
A.7tanα+7tanβ B.
C. D.7tanα-7tanβ
11.某数学研究性学习小组制作了如下的三角函数计算图尺,在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的O刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出cos∠AOB的值是( )
A. B. C. D.
12.Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于D,M在AC延长线上,N在BD上,MN经过BC中点E,MD=MN,若sinA=,则的值为( )
A. B. C. D.
二.填空题(共5小题)
13.Rt△ABC中,若两直角边a,b满足,则三角形中最小的角的正切值是 ______.
14.如图,某中学九(9)班数学课外活动小组在河边测量河宽AB(这段河流的两岸平行),他们在点C测得∠ACB=30°,点D测得∠ADB=60°,CD=80m,则河宽AB为 ______m.
15.(2025 柳州三模)如图,是一条坡角为18°的滑雪道,滑雪道AC长为500米,则滑雪道的坡顶到坡底的竖直高度AB的长为______米(精确到0.1米).(参考数据:sin18°≈0.309,cos18°≈0.951,tan18°≈0.325).
16.如图,一棵大树被台风拦腰刮断,树根A到刮断点P的长度是4m,折断部分PB与地面成的夹角α,那么原来树的高度是 ______m.(用含有α的代数式表示)
17.小怿从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.若光从真空射入某介质,入射角为α,折射角为β,且,β=30°,求该介质的折射率______.
三.解答题(共5小题)
18.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
19.(2025 常德三模)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB的高度,具体过程如下:如图,将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,求黄鹤楼的高度(参考数据:tan63°≈2).
20.(2025 三原县二模)如图,这是雨伞打开后的示意图,AP是伞柄,AB,AC是伞骨,=30cm,点D为伞圈,AP平分∠BAC,伞完全张开时∠BAC=120°.雨往往斜向落下,假设雨线之间是平行的.某一天,雨线BM与地面之间的夹角为60°,小伟站在伞圈点D正下方的点G处,将小伟的身高记为GH,此时他身上被雨淋湿,测得BN=150cm.求伞至少向下移动多少cm的距离,才能使得小伟站在点G处不被雨淋湿身上.
21.(2025 信都区二模)如图是嘉淇为某公司设计的公司标志示意图,四边形ABCD与四边形FECG是两个全等的平行四边形,点B、C、E在同一条直线上,点Q、N分别在边AD、GF上,且PM∥BE.已知点P到BC的距离为5,EF=5.56cm,∠DCG=30°.
(1)求点A到BC的距离;
(2)若PQ=4.64cm,试通过计算说明PQ∥CD.
[注:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73]
22.消防车是火灾消防救援的主要装备,确保人民生命财产安全.图1是某种消防车云梯,图2是其侧面示意图,点D,B,O在同一直线上,DO可绕着点O旋转,点O,A,C在同一水平线上,其中BD可伸缩,套管OB的长度不变,通过液压杆AB长度来调整∠DOC的大小,在某种工作状态下测得液压杆AB=°.
(1)求BO的长;
(2)消防人员在云梯末端点D高空作业时,将BD伸长到最大长度6m,再将云梯DO绕着点O顺时针旋转34°,此时云梯末端D的铅直高度升高了多少?(参考数据sin64°≈0.90,cos64°≈0.44)
浙教版九年级下 第1章 解直角三角形 单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、A 3、D 4、C 5、A 6、A 7、D 8、B 9、C 10、B 11、A 12、A
二.填空题(共5小题)
13、; 14、69; 15、154.5; 16、(4+); 17、;
三.解答题(共5小题)
18、解:在Rt△BCD中,∵CD=3、BD=5,
∴BC===4,
又AC=AD+CD=8,
∴AB===4,
则sinA===,
cosA===,
tanA===.
19、解:将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,如图,延长BA交距水平地面102m的水平线于点D,
依题意,有三个角都是直角的四边形是矩形,
∴BD=102m,
设AD=x cm,
∵∠DCA=45°,
∴DC=AD=x cm,
∴,
∴DC=AD≈51,
∴AB=BD-AD=102-51≈51(m),
∴黄鹤楼的高度约为51m.
20、解:如图,设AG与BC交于点O,与BM交于点Q.
∵∠BAC=120°,AP 平分∠BAC,
∴∠BAO=60°,
在Rt△ABO中,AB=3AE=90cm,∠BAO=60°,
∴BO=AB sin,
∴.
在Rt△BMN中,BN=150cm,∠BMN=60°,
∴.
在Rt△QGM中,.
答:伞至少向下移动15cm的距离,才能使得小伟站在点G处不被雨淋湿身上.
21、解:(1)过点A作AH⊥BC,垂足落在CB的延长线上,
∵四边形ABCD与四边形FECG是两个全等的平行四边形,
∴∠DCB=∠GCE,EF=AB,
∵∠DCG=30°,
∴∠DCB=75°.
∵AB∥CD,
∴∠ABH=∠DCB=75°,
∴AH=ABsin75°≈5.4(cm),
∴点A到BC的距离为5.4cm;
(2)过点P作PO⊥AD于O点,
∵点P到BC的距离为5,
∴PO=9.9-5.4=4.5,
∵,
∴∠PQO=75°.
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=75°,
∴∠PQO=∠DAB,
∴AB∥PQ,
∴PQ∥CD.
22、解:(1)如图1,过点B作BE⊥OC,垂足为E,
∵∠BAC=60°,∠DOC=30°,
∴∠ABO=∠DOC=30°,
∴OA=AB=m,
在Rt△AEB 中,BAC=60°,
∴∠ABE=30°,
∴AE=AB=,BE=AE=2,
在Rt△OEB 中,∠DOC=30°,
∴OB=2BE=4m;
(2)如图2,过点D作DN⊥OC,垂足为N,
在Rt△DNO中,OD=OB+BD=4+6=10,
∴DN=OD sin∠DON,
当∠DON=30°时,
DN=OD sin64°≈10×=5(m),
当∠DON=30°+34°=64°时,
DN=OD sin64°≈10×0.90=9(m),
9-5=4(米),
∴此时云梯末端D的铅直高度升高了4米.
