浙教版八年级下 第4章 平行四边形 单元测试(含答案)
文档属性
| 名称 | 浙教版八年级下 第4章 平行四边形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 118.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 23:00:54 | ||
图片预览


文档简介
浙教版八年级下 第4章 平行四边形 单元测试
一.选择题(共12小题)
1.(2025 崂山区校级三模)“汉服”又称“衣冠”、“衣裳”,是中国“衣冠上国”、“礼仪之邦”、“绵绣中华”的体现.以下四种汉服常用装饰纹样中,既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.若一个多边形的内角和为900°,则这个多边形的边数为( )
A.5 B.7 C.10 D.12
3.如图,正六边形ABCDEF和等腰Rt△ABH的一边重合,∠HAB=90°,则直线HB与直线CD所夹锐角的度数为( )
A.15° B.20° C.25° D.30°
4.已知在平行四边形ABCD中,AC=6,E是AD上一点,△DCE的周长是平行四边形ABCD周长的一半,且EC=4,连接EO,则EO的长为( )
A.3 B.5 C.2 D.
5.如图,在 ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若 ABCD的周长为24,则△CED的周长为( )
A.6 B.12 C.18 D.22
6.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=3,AE=2,则DE的长为( )
A. B. C.5 D.6
7.如图,已知四边形ABCD中,AC⊥BD,AC=6,BD=8,点E、F分别是边AD、BC的中点,连接EF,则EF的长是( )
A. B.5 C. D.10
8.如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 B.6 C.8 D.10
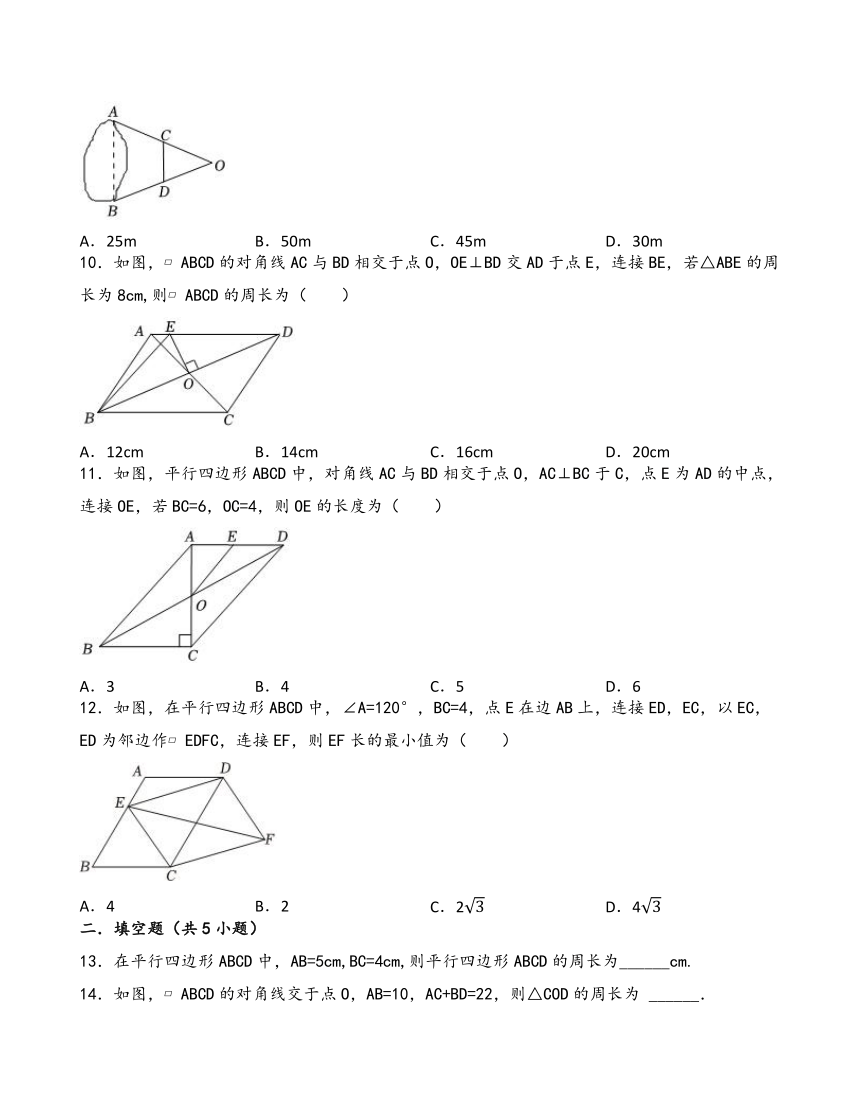
9.如图,为测量位于一水塘旁的两点A,B间的直线距离,在水塘所在的同一水平面上任选一点O,连接OA,OB,再分别取OA,OB的中点C,D,量得CD=25m,则A,B之间的直线距离是( )
A.25m B.50m C.45m D.30m
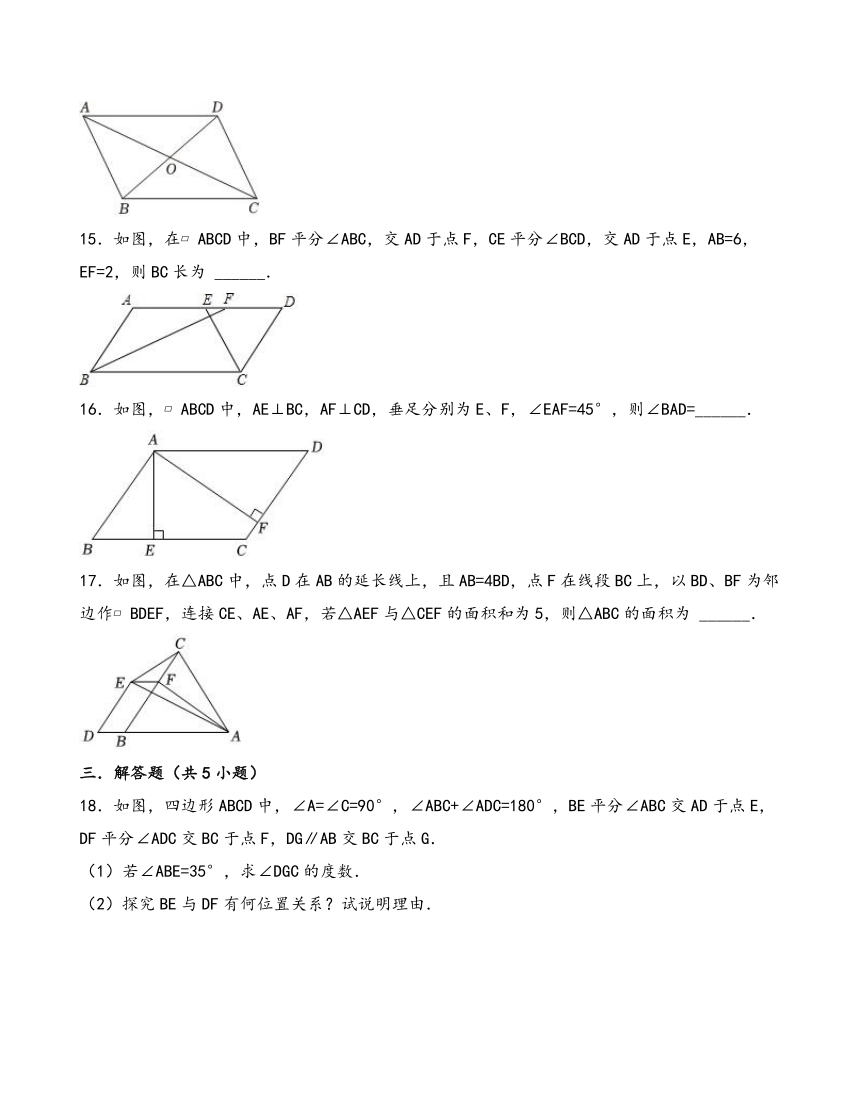
10.如图, ABCD的对角线AC与BD相交于点O,OE⊥BD交AD于点E,连接BE,若△ABE的周长为8cm,则 ABCD的周长为( )
A.12cm B.14cm C.16cm D.20cm
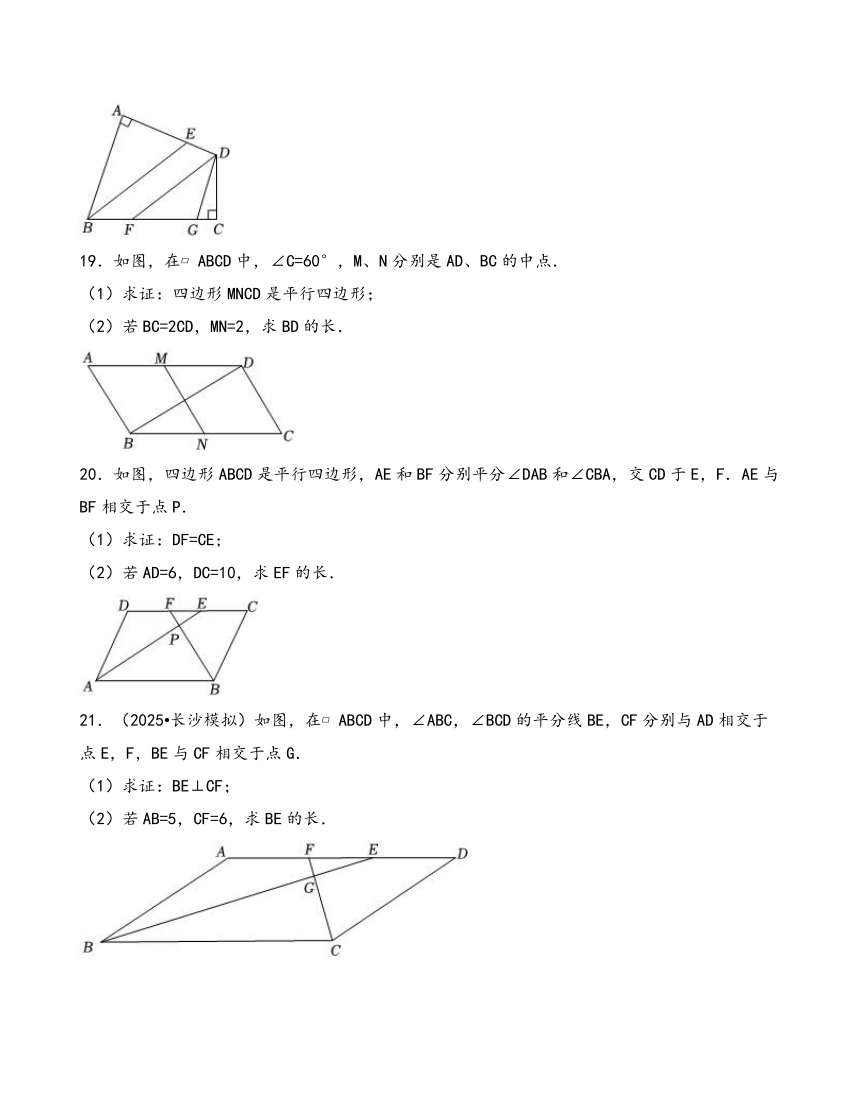
11.如图,平行四边形ABCD中,对角线AC与BD相交于点O,AC⊥BC于C,点E为AD的中点,连接OE,若BC=6,OC=4,则OE的长度为( )
A.3 B.4 C.5 D.6
12.如图,在平行四边形ABCD中,∠A=120°,BC=4,点E在边AB上,连接ED,EC,以EC,ED为邻边作 EDFC,连接EF,则EF长的最小值为( )
A.4 B.2 C.2 D.4
二.填空题(共5小题)
13.在平行四边形ABCD中,AB=5cm,BC=4cm,则平行四边形ABCD的周长为______cm.
14.如图, ABCD的对角线交于点O,AB=10,AC+BD=22,则△COD的周长为 ______.
15.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为 ______.
16.如图, ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=______.
17.如图,在△ABC中,点D在AB的延长线上,且AB=4BD,点F在线段BC上,以BD、BF为邻边作 BDEF,连接CE、AE、AF,若△AEF与△CEF的面积和为5,则△ABC的面积为 ______.
三.解答题(共5小题)
18.如图,四边形ABCD中,∠A=∠C=90°,∠ABC+∠ADC=180°,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,DG∥AB交BC于点G.
(1)若∠ABE=35°,求∠DGC的度数.
(2)探究BE与DF有何位置关系?试说明理由.
19.如图,在 ABCD中,∠C=60°,M、N分别是AD、BC的中点.
(1)求证:四边形MNCD是平行四边形;
(2)若BC=2CD,MN=2,求BD的长.
20.如图,四边形ABCD是平行四边形,AE和BF分别平分∠DAB和∠CBA,交CD于E,F.AE与BF相交于点P.
(1)求证:DF=CE;
(2)若AD=6,DC=10,求EF的长.
21.(2025 长沙模拟)如图,在 ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E,F,BE与CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=5,CF=6,求BE的长.
22.在△ABC中,D,E分别是AB,BC边的中点,连接AE,过点C作CF∥AE交DE的延长线于点F,连接AF交BC于点O.
(1)求证:四边形AEFC为平行四边形;
(2)若∠ACB=90°,DE=1,AE=,求△AOB的面积.
浙教版八年级下 第4章 平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、B 3、A 4、D 5、B 6、B 7、B 8、C 9、B 10、C 11、C 12、D
二.填空题(共5小题)
13、18; 14、21; 15、10; 16、135°; 17、20;
三.解答题(共5小题)
18、解:(1)∵BE平分∠ABC,∠ABE=35°,
∴∠ABC=2∠ABE=2×35°=70°,
∵DG∥AB,
∴∠DGC=∠ABC=70°;
(2)BE∥DF;理由如下:
∵BE平分∠ABC,DF平分∠ADC,
∴,,
∵∠ABC+∠ADC=180°,
∴∠ABE+∠ADF=(∠ABC+∠ADC)=90°,
∵∠A=90°,
∴∠ABE+∠AEB=90°,
∴∠ADF=∠AEB,
∴BE∥DF.
19、(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC,
∵M、N分别是AD、BC的中点,
∴DM∥CN,MD=AM=AD,CN=BN=BC,
∴DM=CN,
∴四边形MNCD是平行四边形.
(2)解:连接DN,
∵BC=2CD,CD=MN=2,
∴BC=4,CD=BC,
∵CN=BN=BC,
∴CD=CN=BN,
∵∠C=60°,
∴△CDN是等边三角形,
∴DN=CN=BN,∠CND=∠CDN=60°,
∴∠NDB=∠NBD,
∵∠CND=∠NDB+∠NBD=2∠NDB=60°,
∴∠NDB=30°,
∴∠BDC=∠CDN+∠NDB=90°,
∴BD===2,
∴BD的长是2.
20、解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC,
∴∠DEA=∠BAE,∠CFB=∠ABF,
∵AE平分∠DAB,BF平分∠CBA,分别交CD于E,F,AE与BF相交于点P,
∴∠DAE=∠BAE,∠CBF=∠ABF,
∴∠DAE=∠DEA,∠CBF=∠CFB,
∴AD=DE,BC=CF,
∵AD=BC,
∴DE=CF,
∴DE-EF=CF-EF,
∴DF=CE;
(2)∵AD=6,
∴DE=CF=AD=6,
∵DC=10,
∴CE=DC-DE=4,
∴EF=CF-CE=2.
21、解:(1)∵BE平分∠ABC,CF平分∠BCD,
∴.
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴,
∴∠CGB=90°,
∴BE⊥CF.
(2)过点A作AP∥FC,交BC于点P,交BE于点H,
∵AD∥BC,
∴AP=CF=6,
∵∠ABE=∠CBE.
在 ABCD中,AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=5.
∵AP∥FC,由(1)知,BE⊥CF,
∴BE⊥AP,
∴,,
同理可得:AB=AE=5
∴
∴BH2+AH2=AB2,
即BH2+32=52,
故BH=4,
∴BE=2BH=8.
22、(1)证明:∵D,E分别是AB,BC边的中点,
∴DE是△ABC的中位线,
∴AC=2DE,DE∥AC,
即EF∥AC,
又∵CF∥AE,
∴四边形AEFC为平行四边形;
(2)解:由(1)可知:AC=2DE,四边形AEFC为平行四边形,
∵∠ACB=90°,DE=1,AE=,
∴AC=2,设OC=OD=a,
∴CE=2a,
∵点E是BC的中点,
∴BE=CE=2a,
∴OB=BE+OE=3a,
在Rt△ACE中,由勾股定理得:AC2+CE2=AE2,
∴22+(2a)2=13,
解得:a=,a=(不合题意,舍去),
∴OB=3a=,
∴△AOB的面积为:OB AC==.
一.选择题(共12小题)
1.(2025 崂山区校级三模)“汉服”又称“衣冠”、“衣裳”,是中国“衣冠上国”、“礼仪之邦”、“绵绣中华”的体现.以下四种汉服常用装饰纹样中,既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.若一个多边形的内角和为900°,则这个多边形的边数为( )
A.5 B.7 C.10 D.12
3.如图,正六边形ABCDEF和等腰Rt△ABH的一边重合,∠HAB=90°,则直线HB与直线CD所夹锐角的度数为( )
A.15° B.20° C.25° D.30°
4.已知在平行四边形ABCD中,AC=6,E是AD上一点,△DCE的周长是平行四边形ABCD周长的一半,且EC=4,连接EO,则EO的长为( )
A.3 B.5 C.2 D.
5.如图,在 ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若 ABCD的周长为24,则△CED的周长为( )
A.6 B.12 C.18 D.22
6.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=3,AE=2,则DE的长为( )
A. B. C.5 D.6
7.如图,已知四边形ABCD中,AC⊥BD,AC=6,BD=8,点E、F分别是边AD、BC的中点,连接EF,则EF的长是( )
A. B.5 C. D.10
8.如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 B.6 C.8 D.10
9.如图,为测量位于一水塘旁的两点A,B间的直线距离,在水塘所在的同一水平面上任选一点O,连接OA,OB,再分别取OA,OB的中点C,D,量得CD=25m,则A,B之间的直线距离是( )
A.25m B.50m C.45m D.30m
10.如图, ABCD的对角线AC与BD相交于点O,OE⊥BD交AD于点E,连接BE,若△ABE的周长为8cm,则 ABCD的周长为( )
A.12cm B.14cm C.16cm D.20cm
11.如图,平行四边形ABCD中,对角线AC与BD相交于点O,AC⊥BC于C,点E为AD的中点,连接OE,若BC=6,OC=4,则OE的长度为( )
A.3 B.4 C.5 D.6
12.如图,在平行四边形ABCD中,∠A=120°,BC=4,点E在边AB上,连接ED,EC,以EC,ED为邻边作 EDFC,连接EF,则EF长的最小值为( )
A.4 B.2 C.2 D.4
二.填空题(共5小题)
13.在平行四边形ABCD中,AB=5cm,BC=4cm,则平行四边形ABCD的周长为______cm.
14.如图, ABCD的对角线交于点O,AB=10,AC+BD=22,则△COD的周长为 ______.
15.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为 ______.
16.如图, ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=______.
17.如图,在△ABC中,点D在AB的延长线上,且AB=4BD,点F在线段BC上,以BD、BF为邻边作 BDEF,连接CE、AE、AF,若△AEF与△CEF的面积和为5,则△ABC的面积为 ______.
三.解答题(共5小题)
18.如图,四边形ABCD中,∠A=∠C=90°,∠ABC+∠ADC=180°,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,DG∥AB交BC于点G.
(1)若∠ABE=35°,求∠DGC的度数.
(2)探究BE与DF有何位置关系?试说明理由.
19.如图,在 ABCD中,∠C=60°,M、N分别是AD、BC的中点.
(1)求证:四边形MNCD是平行四边形;
(2)若BC=2CD,MN=2,求BD的长.
20.如图,四边形ABCD是平行四边形,AE和BF分别平分∠DAB和∠CBA,交CD于E,F.AE与BF相交于点P.
(1)求证:DF=CE;
(2)若AD=6,DC=10,求EF的长.
21.(2025 长沙模拟)如图,在 ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E,F,BE与CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=5,CF=6,求BE的长.
22.在△ABC中,D,E分别是AB,BC边的中点,连接AE,过点C作CF∥AE交DE的延长线于点F,连接AF交BC于点O.
(1)求证:四边形AEFC为平行四边形;
(2)若∠ACB=90°,DE=1,AE=,求△AOB的面积.
浙教版八年级下 第4章 平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、B 3、A 4、D 5、B 6、B 7、B 8、C 9、B 10、C 11、C 12、D
二.填空题(共5小题)
13、18; 14、21; 15、10; 16、135°; 17、20;
三.解答题(共5小题)
18、解:(1)∵BE平分∠ABC,∠ABE=35°,
∴∠ABC=2∠ABE=2×35°=70°,
∵DG∥AB,
∴∠DGC=∠ABC=70°;
(2)BE∥DF;理由如下:
∵BE平分∠ABC,DF平分∠ADC,
∴,,
∵∠ABC+∠ADC=180°,
∴∠ABE+∠ADF=(∠ABC+∠ADC)=90°,
∵∠A=90°,
∴∠ABE+∠AEB=90°,
∴∠ADF=∠AEB,
∴BE∥DF.
19、(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC,
∵M、N分别是AD、BC的中点,
∴DM∥CN,MD=AM=AD,CN=BN=BC,
∴DM=CN,
∴四边形MNCD是平行四边形.
(2)解:连接DN,
∵BC=2CD,CD=MN=2,
∴BC=4,CD=BC,
∵CN=BN=BC,
∴CD=CN=BN,
∵∠C=60°,
∴△CDN是等边三角形,
∴DN=CN=BN,∠CND=∠CDN=60°,
∴∠NDB=∠NBD,
∵∠CND=∠NDB+∠NBD=2∠NDB=60°,
∴∠NDB=30°,
∴∠BDC=∠CDN+∠NDB=90°,
∴BD===2,
∴BD的长是2.
20、解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC,
∴∠DEA=∠BAE,∠CFB=∠ABF,
∵AE平分∠DAB,BF平分∠CBA,分别交CD于E,F,AE与BF相交于点P,
∴∠DAE=∠BAE,∠CBF=∠ABF,
∴∠DAE=∠DEA,∠CBF=∠CFB,
∴AD=DE,BC=CF,
∵AD=BC,
∴DE=CF,
∴DE-EF=CF-EF,
∴DF=CE;
(2)∵AD=6,
∴DE=CF=AD=6,
∵DC=10,
∴CE=DC-DE=4,
∴EF=CF-CE=2.
21、解:(1)∵BE平分∠ABC,CF平分∠BCD,
∴.
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴,
∴∠CGB=90°,
∴BE⊥CF.
(2)过点A作AP∥FC,交BC于点P,交BE于点H,
∵AD∥BC,
∴AP=CF=6,
∵∠ABE=∠CBE.
在 ABCD中,AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=5.
∵AP∥FC,由(1)知,BE⊥CF,
∴BE⊥AP,
∴,,
同理可得:AB=AE=5
∴
∴BH2+AH2=AB2,
即BH2+32=52,
故BH=4,
∴BE=2BH=8.
22、(1)证明:∵D,E分别是AB,BC边的中点,
∴DE是△ABC的中位线,
∴AC=2DE,DE∥AC,
即EF∥AC,
又∵CF∥AE,
∴四边形AEFC为平行四边形;
(2)解:由(1)可知:AC=2DE,四边形AEFC为平行四边形,
∵∠ACB=90°,DE=1,AE=,
∴AC=2,设OC=OD=a,
∴CE=2a,
∵点E是BC的中点,
∴BE=CE=2a,
∴OB=BE+OE=3a,
在Rt△ACE中,由勾股定理得:AC2+CE2=AE2,
∴22+(2a)2=13,
解得:a=,a=(不合题意,舍去),
∴OB=3a=,
∴△AOB的面积为:OB AC==.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
