浙教版八年级下 第6章 反比例函数 单元测试(含答案)
文档属性
| 名称 | 浙教版八年级下 第6章 反比例函数 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 96.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 23:03:39 | ||
图片预览


文档简介
浙教版八年级下 第6章 反比例函数 单元测试
一.选择题(共12小题)
1.下列关系式中,y是x的反比例函数的是( )
A.y=x B.y=2x2 C. D.
2.反比例函数y=-的比例系数是( )
A.-3 B.3 C.- D.
3.反比例函数y=(m>0,x>0)的图象位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知点(x1,y1)、(x2,y2)是反比例函数图象上的点,若x1>0>x2,则一定成立的是( )
A.y1>y2>0 B.y1>0>y2 C.0>y1>y2 D.y2>0>y1
5.已知点M(-2,3)在反比例函数y=的图象上,下列各点中,一定在该函数图象上的是( )
A.(3,-2) B.(-2,-3) C.(2,3) D.(3,2)
6.如果在反比例函数图象的每一支上,y随x的增大而增大,那么t的取值范围是( )
A. B. C. D.
7.如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=(x>0)的图象分别交BA,BC于点D,E.当AD:BD=1:3,且△BDE的面积为18时,则k的值是( )
A.9.6 B.12 C.14.4 D.16
8.(2025 万山区三模)如图,在平面直角坐标系中,Rt△ABO的直角边AB与反比例函数的图象交于点C,若点C为AB的中点,△ABO的面积为6,则k的值为( )
A.6 B.3 C.2 D.1
9.>如图,在平面直角坐标系中,反比例函数与正比例函数的图象交于A(m,3),B两点,当y1<y2时,x的取值范围是( )
A.x>4 B.-4<x<0或x>4
C.x<-4或0<x<4 D.-4<x<4
10.如图,在平面直角坐标系中,矩形ABCO的两边OA,OC落在坐标轴上,反比例函数y=的图象分别交BC,OB于点D,点E,且,若S△AOE=12,则k的值为( )
A.-12 B.- C.-16 D.-12
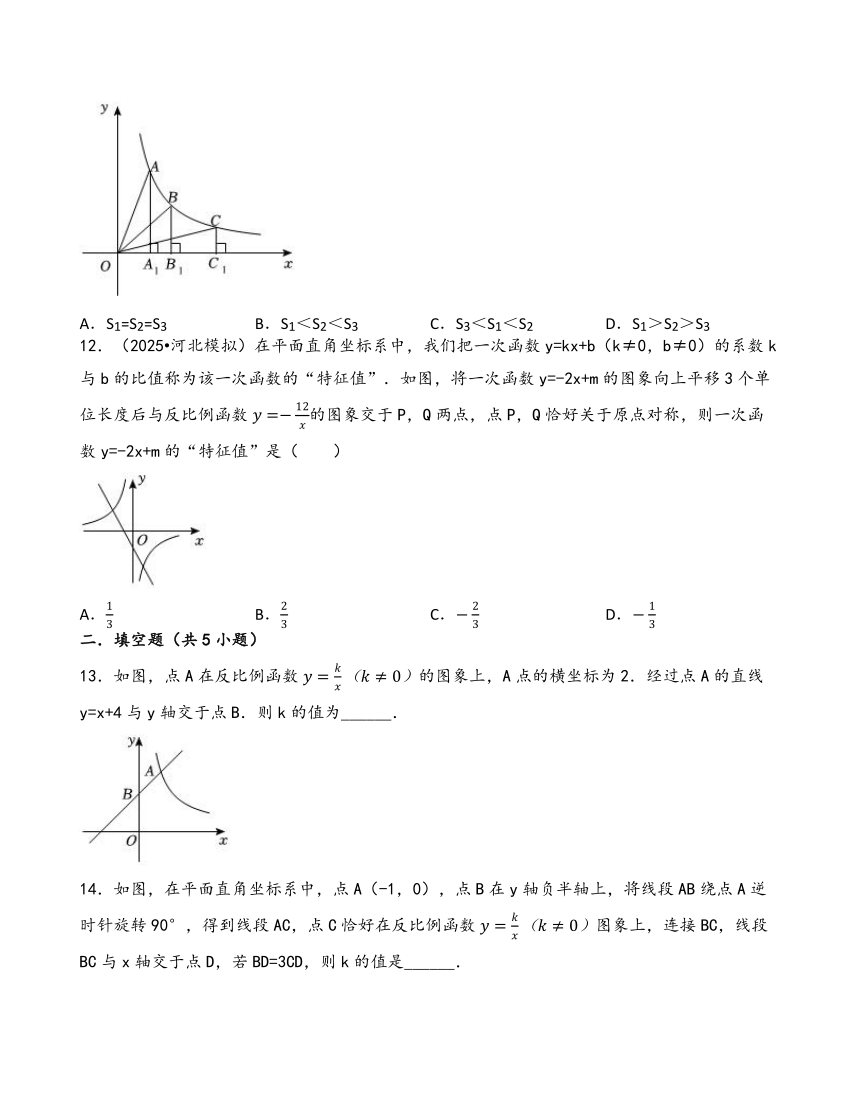
11.如图,点A、B、C在反比例函数的图象上,过这三点分别向x轴作垂线,垂足分别为A1、B1、C1,则△AOA1、△BOB1、△COC1的面积S1、S2、S3之间的关系为( )
A.S1=S2=S3 B.S1<S2<S3 C.S3<S1<S2 D.S1>S2>S3
12.(2025 河北模拟)在平面直角坐标系中,我们把一次函数y=kx+b(k≠0,b≠0)的系数k与b的比值称为该一次函数的“特征值”.如图,将一次函数y=-2x+m的图象向上平移3个单位长度后与反比例函数的图象交于P,Q两点,点P,Q恰好关于原点对称,则一次函数y=-2x+m的“特征值”是( )
A. B. C. D.
二.填空题(共5小题)
13.如图,点A在反比例函数的图象上,A点的横坐标为2.经过点A的直线y=x+4与y轴交于点B.则k的值为______.
14.如图,在平面直角坐标系中,点A(-1,0),点B在y轴负半轴上,将线段AB绕点A逆时针旋转90°,得到线段AC,点C恰好在反比例函数图象上,连接BC,线段BC与x轴交于点D,若BD=3CD,则k的值是______.
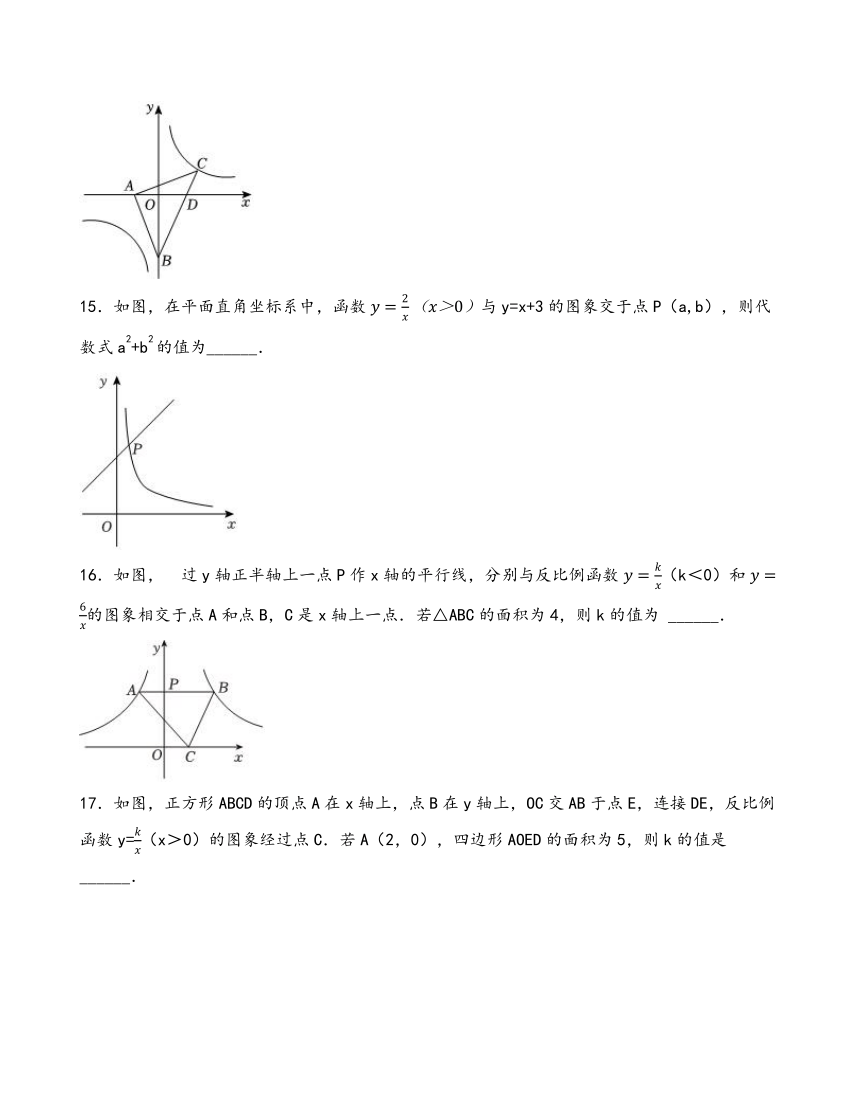
15.如图,在平面直角坐标系中,函数与y=x+3的图象交于点P(a,b),则代数式a2+b2的值为______.
16.如图, 过y轴正半轴上一点P作x轴的平行线,分别与反比例函数(k<0)和的图象相交于点A和点B,C是x轴上一点.若△ABC的面积为4,则k的值为 ______.
17.如图,正方形ABCD的顶点A在x轴上,点B在y轴上,OC交AB于点E,连接DE,反比例函数y=(x>0)的图象经过点C.若A(2,0),四边形AOED的面积为5,则k的值是 ______.
三.解答题(共5小题)
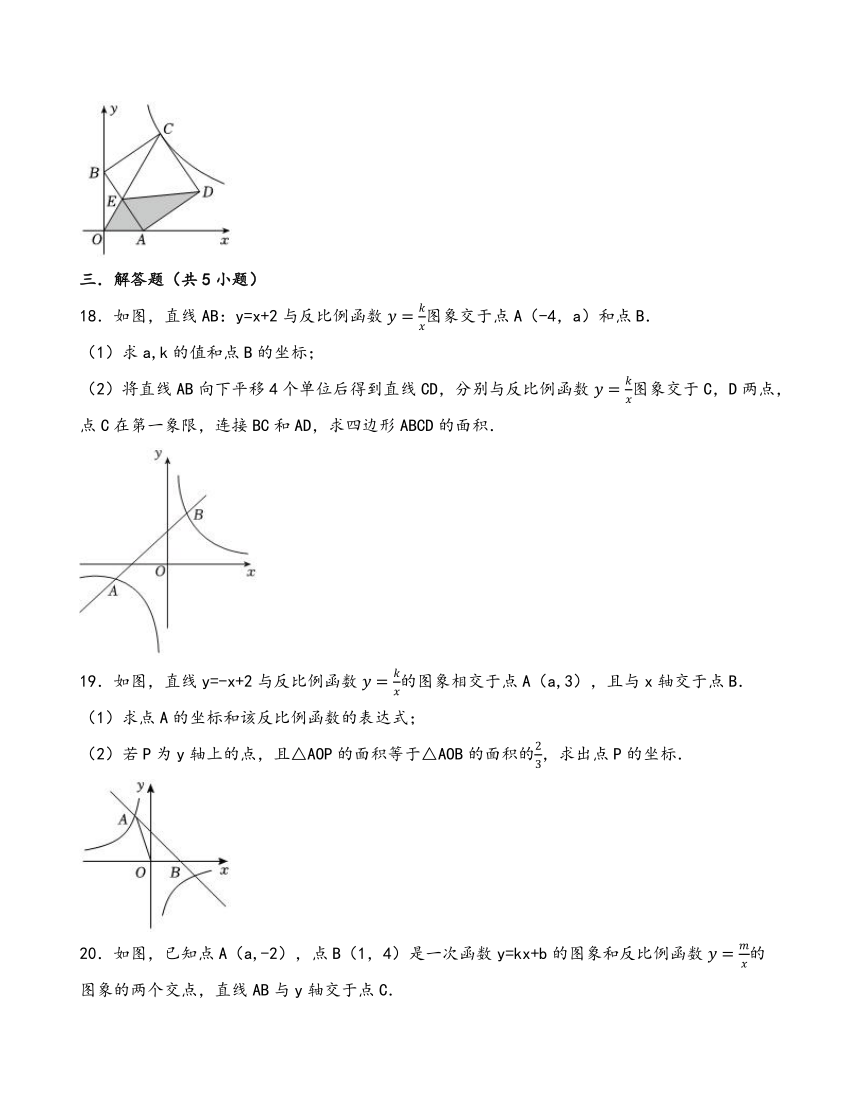
18.如图,直线AB:y=x+2与反比例函数图象交于点A(-4,a)和点B.
(1)求a,k的值和点B的坐标;
(2)将直线AB向下平移4个单位后得到直线CD,分别与反比例函数图象交于C,D两点,点C在第一象限,连接BC和AD,求四边形ABCD的面积.
19.如图,直线y=-x+2与反比例函数的图象相交于点A(a,3),且与x轴交于点B.
(1)求点A的坐标和该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积等于△AOB的面积的,求出点P的坐标.
20.如图,已知点A(a,-2),点B(1,4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)若点P是y轴上一点,且△APB的面积等于3,求点P的坐标;
(3)求不等式的解集.(直接写出答案即可)
21.如图,一次函数y=ax+b的图象与反比例函数的图象相交于A(m,1),B(2,n)两点,与y轴交于点C.
(1)求一次函数的解析式;
(2)设D为线段AC上的一个动点(不包括A,C两点),过点D作DE∥y轴交反比例函数图象于点E,当△CDE的面积是3时,求点E的坐标.
22.如图1,反比例函数与一次函数y=k2x+b(k2≠0)的图象交于点A(-1,3),点B(m,1),一次函数与x轴、y轴相交于点C、D.
(1)①求反比例函数和一次函数y=k2x+b的表达式;
②直接写出关于x的不等式的取值范围.
(2)如图2,点E为一次函数y=k2x+b的图象上一点,过点E作反比例函数,连接OE,若△OEC面积为S,当2≤S≤4时,求k3的取值范围.
浙教版八年级下 第6章 反比例函数 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、A 4、D 5、A 6、C 7、D 8、A 9、B 10、C 11、A 12、B
二.填空题(共5小题)
13、12; 14、2; 15、13; 16、-2; 17、15;
三.解答题(共5小题)
18、解:(1)当x=-4时,y=x+2=-2,
∴A(-4,-2),即a=-2,
将A(-4,-2)代入中,有k=8,
∴反比例函数解析式为:,
联立:,
解得:,或,
∴B(2,4),
综上所述:a=-2,k=8,B(2,4);
(2)由条件可知直线CD:y=x+2-4=x-2,
联立:,
解得:,或者,
∴C(4,2),D(-2,-4),
连接AC,如图,
由条件可知AB2=(2+4)2+(4+2)2=72,AC2=(4+4)2+(2+2)2=80,BC2=(4-2)2+(2-4)2=8,
∴AC2=AB2+BC2,,,
∴△ABC是直角三角形,且∠ABC=90°,
同理可证明∠ADC=∠BAD=∠BCD=90°,
∴四边形ABCD是矩形,
∴S矩形ABCD=AB BC=24.
19、解:(1)由条件可知3=-a+2.
∴a=-1.
∴A(-1,3).
由条件可得.
∴k=-3.
∴该反比例函数的表达式为;
(2)∵直线y=-x+2与x轴相交于点B.
∴B(2,0),
∴,
∵△AOP的面积是△AOB的面积的,
∴S△AOP=2,
设P(0,n),
∴,
∴n=±4,
∴P的坐标为(0,4)或(0,-4).
20、解:(1)由条件可知m=4.a=-2,
∴A(-2,-2),
又∵A(-2,-2),B(1,4)是一次函数y=kx+b图象上的点,
联立
解得k=2,b=2,
∴反比例函数的关系式为:;一次函数的关系式为:y=2x+2.
(2)在y=2x+2中,令x=0,则y=2,
∴C(0,2).
设P(0,y0),则PC=|y0-2|.
∵A(-2,-2),B(1,4),
∴|xB-xA|=|1-(-2)|=3,
S△APB=S△APC+S△BPC,
.
∴,即|y0-2|=2.
当y0-2=2时,y0=4;当y0-2=-2时,y0=0.
∴点P的坐标为(0,4)或(0,0).
(3)不等式的解集,就是一次函数y=kx+b的图象在反比例函数图象下方时x的取值范围.
从图象上看,当x<-2或0<x<1时,一次函数y=2x+2的图象在反比例函数图象下方.
∴不等式的解集为0<x<1或x<-2.
21、解:(1)∵一次函数y=ax+b的图象与反比例函数的图象相交于A(m,1),B(2,n)两点,
∴把A(m,1),B(2,n)代入中,得:m=-6,n=-3,
∴A(-6,1),B(2,-3),
又∵A(-6,1),B(2,-3)在一次函数y=ax+b的图象上,
∴,
解得,
∴一次函数的解析式为;
(2)当x=0时,y=-2,
∴C(0,-2),
设点D的坐标为,则,
∴,
∴,
解得:m1=-4,m2=0(不合题意,舍去),
∴.
22、解:(1)①∵点A(-1,3),点B(m,1)在反比例函数上,
∴k1=-1×3=m×1=-3,
∴k1=-3,m=-3
∴反比例函数的关系式为:,
将点A(-1,3),B(-3,1)代入y=k2x+b(k2≠0)
得,解得,
∴一次函数的关系式为:y=x+4;
②由图象可知,关于x的不等式的取值范围是:-3<x<-1或x>0;
(2)设E点坐标为(a,a+4)由题意知
∵2≤s≤4,
∴2≤2|a|≤4,1≤|a|≤2,
∵a<0,
∴-2≤a≤-1,
当a=-2时,a+4=2,k3=a (a+4)=-4;
当a=-1时,a+4=3,k3=a (a+4)=-3;
因此,-4≤k3≤-3.
一.选择题(共12小题)
1.下列关系式中,y是x的反比例函数的是( )
A.y=x B.y=2x2 C. D.
2.反比例函数y=-的比例系数是( )
A.-3 B.3 C.- D.
3.反比例函数y=(m>0,x>0)的图象位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知点(x1,y1)、(x2,y2)是反比例函数图象上的点,若x1>0>x2,则一定成立的是( )
A.y1>y2>0 B.y1>0>y2 C.0>y1>y2 D.y2>0>y1
5.已知点M(-2,3)在反比例函数y=的图象上,下列各点中,一定在该函数图象上的是( )
A.(3,-2) B.(-2,-3) C.(2,3) D.(3,2)
6.如果在反比例函数图象的每一支上,y随x的增大而增大,那么t的取值范围是( )
A. B. C. D.
7.如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=(x>0)的图象分别交BA,BC于点D,E.当AD:BD=1:3,且△BDE的面积为18时,则k的值是( )
A.9.6 B.12 C.14.4 D.16
8.(2025 万山区三模)如图,在平面直角坐标系中,Rt△ABO的直角边AB与反比例函数的图象交于点C,若点C为AB的中点,△ABO的面积为6,则k的值为( )
A.6 B.3 C.2 D.1
9.>如图,在平面直角坐标系中,反比例函数与正比例函数的图象交于A(m,3),B两点,当y1<y2时,x的取值范围是( )
A.x>4 B.-4<x<0或x>4
C.x<-4或0<x<4 D.-4<x<4
10.如图,在平面直角坐标系中,矩形ABCO的两边OA,OC落在坐标轴上,反比例函数y=的图象分别交BC,OB于点D,点E,且,若S△AOE=12,则k的值为( )
A.-12 B.- C.-16 D.-12
11.如图,点A、B、C在反比例函数的图象上,过这三点分别向x轴作垂线,垂足分别为A1、B1、C1,则△AOA1、△BOB1、△COC1的面积S1、S2、S3之间的关系为( )
A.S1=S2=S3 B.S1<S2<S3 C.S3<S1<S2 D.S1>S2>S3
12.(2025 河北模拟)在平面直角坐标系中,我们把一次函数y=kx+b(k≠0,b≠0)的系数k与b的比值称为该一次函数的“特征值”.如图,将一次函数y=-2x+m的图象向上平移3个单位长度后与反比例函数的图象交于P,Q两点,点P,Q恰好关于原点对称,则一次函数y=-2x+m的“特征值”是( )
A. B. C. D.
二.填空题(共5小题)
13.如图,点A在反比例函数的图象上,A点的横坐标为2.经过点A的直线y=x+4与y轴交于点B.则k的值为______.
14.如图,在平面直角坐标系中,点A(-1,0),点B在y轴负半轴上,将线段AB绕点A逆时针旋转90°,得到线段AC,点C恰好在反比例函数图象上,连接BC,线段BC与x轴交于点D,若BD=3CD,则k的值是______.
15.如图,在平面直角坐标系中,函数与y=x+3的图象交于点P(a,b),则代数式a2+b2的值为______.
16.如图, 过y轴正半轴上一点P作x轴的平行线,分别与反比例函数(k<0)和的图象相交于点A和点B,C是x轴上一点.若△ABC的面积为4,则k的值为 ______.
17.如图,正方形ABCD的顶点A在x轴上,点B在y轴上,OC交AB于点E,连接DE,反比例函数y=(x>0)的图象经过点C.若A(2,0),四边形AOED的面积为5,则k的值是 ______.
三.解答题(共5小题)
18.如图,直线AB:y=x+2与反比例函数图象交于点A(-4,a)和点B.
(1)求a,k的值和点B的坐标;
(2)将直线AB向下平移4个单位后得到直线CD,分别与反比例函数图象交于C,D两点,点C在第一象限,连接BC和AD,求四边形ABCD的面积.
19.如图,直线y=-x+2与反比例函数的图象相交于点A(a,3),且与x轴交于点B.
(1)求点A的坐标和该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积等于△AOB的面积的,求出点P的坐标.
20.如图,已知点A(a,-2),点B(1,4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)若点P是y轴上一点,且△APB的面积等于3,求点P的坐标;
(3)求不等式的解集.(直接写出答案即可)
21.如图,一次函数y=ax+b的图象与反比例函数的图象相交于A(m,1),B(2,n)两点,与y轴交于点C.
(1)求一次函数的解析式;
(2)设D为线段AC上的一个动点(不包括A,C两点),过点D作DE∥y轴交反比例函数图象于点E,当△CDE的面积是3时,求点E的坐标.
22.如图1,反比例函数与一次函数y=k2x+b(k2≠0)的图象交于点A(-1,3),点B(m,1),一次函数与x轴、y轴相交于点C、D.
(1)①求反比例函数和一次函数y=k2x+b的表达式;
②直接写出关于x的不等式的取值范围.
(2)如图2,点E为一次函数y=k2x+b的图象上一点,过点E作反比例函数,连接OE,若△OEC面积为S,当2≤S≤4时,求k3的取值范围.
浙教版八年级下 第6章 反比例函数 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、A 4、D 5、A 6、C 7、D 8、A 9、B 10、C 11、A 12、B
二.填空题(共5小题)
13、12; 14、2; 15、13; 16、-2; 17、15;
三.解答题(共5小题)
18、解:(1)当x=-4时,y=x+2=-2,
∴A(-4,-2),即a=-2,
将A(-4,-2)代入中,有k=8,
∴反比例函数解析式为:,
联立:,
解得:,或,
∴B(2,4),
综上所述:a=-2,k=8,B(2,4);
(2)由条件可知直线CD:y=x+2-4=x-2,
联立:,
解得:,或者,
∴C(4,2),D(-2,-4),
连接AC,如图,
由条件可知AB2=(2+4)2+(4+2)2=72,AC2=(4+4)2+(2+2)2=80,BC2=(4-2)2+(2-4)2=8,
∴AC2=AB2+BC2,,,
∴△ABC是直角三角形,且∠ABC=90°,
同理可证明∠ADC=∠BAD=∠BCD=90°,
∴四边形ABCD是矩形,
∴S矩形ABCD=AB BC=24.
19、解:(1)由条件可知3=-a+2.
∴a=-1.
∴A(-1,3).
由条件可得.
∴k=-3.
∴该反比例函数的表达式为;
(2)∵直线y=-x+2与x轴相交于点B.
∴B(2,0),
∴,
∵△AOP的面积是△AOB的面积的,
∴S△AOP=2,
设P(0,n),
∴,
∴n=±4,
∴P的坐标为(0,4)或(0,-4).
20、解:(1)由条件可知m=4.a=-2,
∴A(-2,-2),
又∵A(-2,-2),B(1,4)是一次函数y=kx+b图象上的点,
联立
解得k=2,b=2,
∴反比例函数的关系式为:;一次函数的关系式为:y=2x+2.
(2)在y=2x+2中,令x=0,则y=2,
∴C(0,2).
设P(0,y0),则PC=|y0-2|.
∵A(-2,-2),B(1,4),
∴|xB-xA|=|1-(-2)|=3,
S△APB=S△APC+S△BPC,
.
∴,即|y0-2|=2.
当y0-2=2时,y0=4;当y0-2=-2时,y0=0.
∴点P的坐标为(0,4)或(0,0).
(3)不等式的解集,就是一次函数y=kx+b的图象在反比例函数图象下方时x的取值范围.
从图象上看,当x<-2或0<x<1时,一次函数y=2x+2的图象在反比例函数图象下方.
∴不等式的解集为0<x<1或x<-2.
21、解:(1)∵一次函数y=ax+b的图象与反比例函数的图象相交于A(m,1),B(2,n)两点,
∴把A(m,1),B(2,n)代入中,得:m=-6,n=-3,
∴A(-6,1),B(2,-3),
又∵A(-6,1),B(2,-3)在一次函数y=ax+b的图象上,
∴,
解得,
∴一次函数的解析式为;
(2)当x=0时,y=-2,
∴C(0,-2),
设点D的坐标为,则,
∴,
∴,
解得:m1=-4,m2=0(不合题意,舍去),
∴.
22、解:(1)①∵点A(-1,3),点B(m,1)在反比例函数上,
∴k1=-1×3=m×1=-3,
∴k1=-3,m=-3
∴反比例函数的关系式为:,
将点A(-1,3),B(-3,1)代入y=k2x+b(k2≠0)
得,解得,
∴一次函数的关系式为:y=x+4;
②由图象可知,关于x的不等式的取值范围是:-3<x<-1或x>0;
(2)设E点坐标为(a,a+4)由题意知
∵2≤s≤4,
∴2≤2|a|≤4,1≤|a|≤2,
∵a<0,
∴-2≤a≤-1,
当a=-2时,a+4=2,k3=a (a+4)=-4;
当a=-1时,a+4=3,k3=a (a+4)=-3;
因此,-4≤k3≤-3.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
