浙教版数学九年级上册 第4章 相似三角形 单元测试(含答案)
文档属性
| 名称 | 浙教版数学九年级上册 第4章 相似三角形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 97.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 23:22:36 | ||
图片预览




文档简介
浙教版九年级上 第4章 相似三角形 单元测试
一.选择题(共12小题)
1.若两个相似三角形的相似比为1:4,则这两个三角形面积的比是( )
A.1:2 B.1:4 C.1:8 D.1:16
2.某品牌汽车为了打造更加精美的外观,特将汽车后视镜C设计为整个车身黄金分割点的位置(如图),若该车车身总长AB约为4.14米,则车头A与后视镜C的水平距离约为( )
A.1.58米 B.2.56米 C.3.70米 D.3.82米
3.已知△ABC和△ADE相似,且相似比为,则△ABC和△ADE的面积比为( )
A. B. C. D.
4.若,则等于( )
A. B. C. D.
5.如图,AD∥BE∥CF,若AB=4,BC=8,DE=3,则EF的长是( )
A.1.5 B.6 C.9 D.12
6.如图,在△ABC中,AD是BC边上中线,F是AD上一点,且AF:FD=1:5,连接CF并延长交AB于E,则AE:EB等于( )
A.1:6 B.1:8 C.1:9 D.1:10
7.如图,已知AB∥CD∥EF,AF交BE于点H,下列结论中错误的是( )
A. B. C.= D.=
8.图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,AD与CB相交于点O,AB∥CD,根据图2中的数据可得x的值为( )
A.0.8 B.0.72 C.1.8 D.2
9.(2025 高密市三模)如图,BC=6,∠CBE=60°,BD=2,DF=1.5,F是AC的中点,则AB长为( )
A. B.1 C. D.
10.如图,△ABC被平行四边形所截,边AB被截成三等分,D和E为三等分点,DF∥BC,若图中阴影部分的面积为3,则四边形BCGE的面积记为S,则S的值为( )
A.5 B.6 C.9 D.12
11.如图,已知矩形ABCD,点E是BC边的中点,AB:BC=3:4,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④AC⊥DE,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:
①AM=PN;
②;
③若P是BC中点,AB=3,则;
④BF NF=AF DF;
⑤若PM∥BD,则.
其中正确的结论是( )
A.①②③⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
二.填空题(共5小题)
13.如果3a=5b(a、b均不为0),那么a:b=______.(填比值)
14.若,则= ______.
15.(2025 杏花岭区二模)如图,在△ABC中,AB=AC,E是AB上的一点,BE=2AE,过点B作BD⊥CE交CE的延长线于点D.若BD=3,CD=5,则DE的长为 ______.
16.(2025 裕华区校级三模)如图,水平地面上放置盛有液体的容器,CD是液面线,经测量,AB=8cm,AD=5cm,把长为12cm的木棍EF的一端F探到容器的底部,另一端与点A重合,则没入液体部分GF的长为______cm.
17.如图,在矩形ABCD中,AB=4,BC=3.点E在边CD上,且CE=3,M,N分别是边AB,AD上的点,且BM=AN=1,P是线段BE上的动点,当△PMN是直角三角形时,BP的长为______.
三.解答题(共5小题)
18.如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)如果AD=3.2cm,DB=1.2cm,AE=2.4cm,那么EC的长是多少?
(2)如果AB=5cm,AD=3cm,AC=4cm,哪么EC的长是多少?
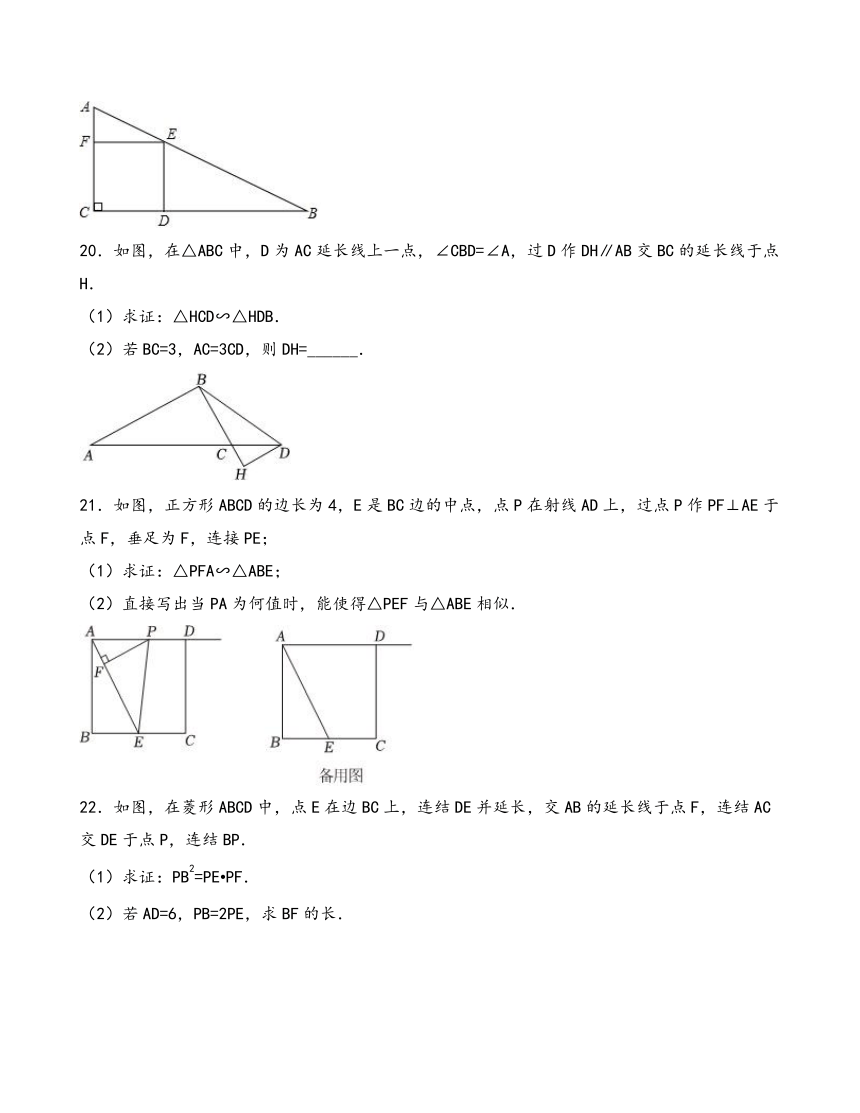
19.如图,在Rt△ABC中,∠C=90°,四边形CDEF是Rt△ABC的内接正方形,已知:AC=3,BC=6.求:
(1)AB的长度;
(2)正方形CDEF的边长.
20.如图,在△ABC中,D为AC延长线上一点,∠CBD=∠A,过D作DH∥AB交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)若BC=3,AC=3CD,则DH=______.
21.如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过点P作PF⊥AE于点F,垂足为F,连接PE;
(1)求证:△PFA∽△ABE;
(2)直接写出当PA为何值时,能使得△PEF与△ABE相似.
22.如图,在菱形ABCD中,点E在边BC上,连结DE并延长,交AB的延长线于点F,连结AC交DE于点P,连结BP.
(1)求证:PB2=PE PF.
(2)若AD=6,PB=2PE,求BF的长.
浙教版九年级上 第4章 相似三角形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、D 4、D 5、B 6、D 7、C 8、B 9、B 10、A 11、A 12、D
二.填空题(共5小题)
13、; 14、3; 15、; 16、; 17、或或;
三.解答题(共5小题)
18、解2:(1)∵DE∥BC,
∴=,即=,
∴EC=0.9(cm);
(2)∵DE∥BC,
∴=,即=,
∴EC=1.6(cm).
19、解:(1)∵∠C=90°且AC=3,BC=6,
由勾股定理知:AB2=AC2+BC2且AB>0,
∴AB=,
故AB的长度为3;
(2)方法一、设正方形CDEF的边长为x,
∴CD=DE=EF=FC=x,
AF=AC-FC=3-x,
∵四边形CDEF是正方形,
∴EF∥CD 且∠EFA=∠EFC=90°,
∴∠AEF=∠ABC,∠EFA=∠EFC,
又∵∠A=∠A,
∴△AEF∽△ABC,
∴,
即,
解得:x=2,
故正方形CDEF的边长为2.
方法二、连接CE,
∵S△ABC=×AC EF+BC DE,
∴3×6=(3+6)×EF,
∴EF=2,
故正方形CDEF的边长为2.
20、(1)证明:在△ABC中,D为AC延长线上一点,∠CBD=∠A,过D作DH∥AB交BC的延长线于点H.
∴∠A=∠HDC
∵∠CBD=∠A,
∴∠HDC=∠CBD,
∵∠H=∠H,
∴△HCD∽△HDB;
(2)解:∵DH∥AB,
∴∠HDC=∠CBD,
∴,
∵BC=3,AC=3CD,
∴,
∴CH=1,
∴BH=BC+CH=3+1=4,
由(1)知△HCD∽△HDB,
∴,
∴DH2=4,
∴DH=2,
故答案为:2.
21、(1)证明:∵正方形ABCD,
∴AD∥BC,∠B=90°,
∴∠DAE=∠AEB,
∵PF⊥AE,
∴∠PFA=90°,
∴∠B=∠PFA,
∴△PFA∽△ABE;
(2)解:当△PFE∽△ABE时,
∴∠PEF=∠AEB,,
由题意可得:,
∴,
∴PF=2EF,
∵AE2=AB2+BE2,
∴,
∴∠DAE=∠AEB,
∴∠PAE=∠PEA,
∴PA=PE,
∵PF⊥AE,
∴,
∴,
∴;
当△EFP∽△ABE时,如图2,
∴∠PEF=∠EAB,
∴AB∥PE,
∴∠PEB=180°-∠B=90°,
∴四边形ABEP是矩形,
∴AP=BE=2,
当PA为5或2时,能使得△PEF与△ABE相似.
22、(1)证明:在菱形ABCD中,点E在边BC上,AC菱形的对角线,
∴AB=CD=CB=AD,∠DCP=∠BCP,AD∥BC,CD∥AB,
∴∠CDP=∠F,
在△DCP与△BCP中,
,
∴△DCP≌△BCP(SAS),
∴∠CDP=∠CBP,
∴∠CBP=∠F,
又∵∠BPE=∠FPB,
∴△BPE∽△FPB,
∴,
∴PB2=PE PF;
(2)解:由(1)得:△BPE∽△FPB,
∴,
∵AD=6,PB=2PE,
∴,
∴BF=2BE,
∵AD∥BC,
∴△BEF∽△ADF,
∴,
∴,
∴AF=2AD,
∵AB=AD=6,
∴AF=2AD=12,
∴BF=AF-AB=6.
一.选择题(共12小题)
1.若两个相似三角形的相似比为1:4,则这两个三角形面积的比是( )
A.1:2 B.1:4 C.1:8 D.1:16
2.某品牌汽车为了打造更加精美的外观,特将汽车后视镜C设计为整个车身黄金分割点的位置(如图),若该车车身总长AB约为4.14米,则车头A与后视镜C的水平距离约为( )
A.1.58米 B.2.56米 C.3.70米 D.3.82米
3.已知△ABC和△ADE相似,且相似比为,则△ABC和△ADE的面积比为( )
A. B. C. D.
4.若,则等于( )
A. B. C. D.
5.如图,AD∥BE∥CF,若AB=4,BC=8,DE=3,则EF的长是( )
A.1.5 B.6 C.9 D.12
6.如图,在△ABC中,AD是BC边上中线,F是AD上一点,且AF:FD=1:5,连接CF并延长交AB于E,则AE:EB等于( )
A.1:6 B.1:8 C.1:9 D.1:10
7.如图,已知AB∥CD∥EF,AF交BE于点H,下列结论中错误的是( )
A. B. C.= D.=
8.图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,AD与CB相交于点O,AB∥CD,根据图2中的数据可得x的值为( )
A.0.8 B.0.72 C.1.8 D.2
9.(2025 高密市三模)如图,BC=6,∠CBE=60°,BD=2,DF=1.5,F是AC的中点,则AB长为( )
A. B.1 C. D.
10.如图,△ABC被平行四边形所截,边AB被截成三等分,D和E为三等分点,DF∥BC,若图中阴影部分的面积为3,则四边形BCGE的面积记为S,则S的值为( )
A.5 B.6 C.9 D.12
11.如图,已知矩形ABCD,点E是BC边的中点,AB:BC=3:4,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④AC⊥DE,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:
①AM=PN;
②;
③若P是BC中点,AB=3,则;
④BF NF=AF DF;
⑤若PM∥BD,则.
其中正确的结论是( )
A.①②③⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
二.填空题(共5小题)
13.如果3a=5b(a、b均不为0),那么a:b=______.(填比值)
14.若,则= ______.
15.(2025 杏花岭区二模)如图,在△ABC中,AB=AC,E是AB上的一点,BE=2AE,过点B作BD⊥CE交CE的延长线于点D.若BD=3,CD=5,则DE的长为 ______.
16.(2025 裕华区校级三模)如图,水平地面上放置盛有液体的容器,CD是液面线,经测量,AB=8cm,AD=5cm,把长为12cm的木棍EF的一端F探到容器的底部,另一端与点A重合,则没入液体部分GF的长为______cm.
17.如图,在矩形ABCD中,AB=4,BC=3.点E在边CD上,且CE=3,M,N分别是边AB,AD上的点,且BM=AN=1,P是线段BE上的动点,当△PMN是直角三角形时,BP的长为______.
三.解答题(共5小题)
18.如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)如果AD=3.2cm,DB=1.2cm,AE=2.4cm,那么EC的长是多少?
(2)如果AB=5cm,AD=3cm,AC=4cm,哪么EC的长是多少?
19.如图,在Rt△ABC中,∠C=90°,四边形CDEF是Rt△ABC的内接正方形,已知:AC=3,BC=6.求:
(1)AB的长度;
(2)正方形CDEF的边长.
20.如图,在△ABC中,D为AC延长线上一点,∠CBD=∠A,过D作DH∥AB交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)若BC=3,AC=3CD,则DH=______.
21.如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过点P作PF⊥AE于点F,垂足为F,连接PE;
(1)求证:△PFA∽△ABE;
(2)直接写出当PA为何值时,能使得△PEF与△ABE相似.
22.如图,在菱形ABCD中,点E在边BC上,连结DE并延长,交AB的延长线于点F,连结AC交DE于点P,连结BP.
(1)求证:PB2=PE PF.
(2)若AD=6,PB=2PE,求BF的长.
浙教版九年级上 第4章 相似三角形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、D 4、D 5、B 6、D 7、C 8、B 9、B 10、A 11、A 12、D
二.填空题(共5小题)
13、; 14、3; 15、; 16、; 17、或或;
三.解答题(共5小题)
18、解2:(1)∵DE∥BC,
∴=,即=,
∴EC=0.9(cm);
(2)∵DE∥BC,
∴=,即=,
∴EC=1.6(cm).
19、解:(1)∵∠C=90°且AC=3,BC=6,
由勾股定理知:AB2=AC2+BC2且AB>0,
∴AB=,
故AB的长度为3;
(2)方法一、设正方形CDEF的边长为x,
∴CD=DE=EF=FC=x,
AF=AC-FC=3-x,
∵四边形CDEF是正方形,
∴EF∥CD 且∠EFA=∠EFC=90°,
∴∠AEF=∠ABC,∠EFA=∠EFC,
又∵∠A=∠A,
∴△AEF∽△ABC,
∴,
即,
解得:x=2,
故正方形CDEF的边长为2.
方法二、连接CE,
∵S△ABC=×AC EF+BC DE,
∴3×6=(3+6)×EF,
∴EF=2,
故正方形CDEF的边长为2.
20、(1)证明:在△ABC中,D为AC延长线上一点,∠CBD=∠A,过D作DH∥AB交BC的延长线于点H.
∴∠A=∠HDC
∵∠CBD=∠A,
∴∠HDC=∠CBD,
∵∠H=∠H,
∴△HCD∽△HDB;
(2)解:∵DH∥AB,
∴∠HDC=∠CBD,
∴,
∵BC=3,AC=3CD,
∴,
∴CH=1,
∴BH=BC+CH=3+1=4,
由(1)知△HCD∽△HDB,
∴,
∴DH2=4,
∴DH=2,
故答案为:2.
21、(1)证明:∵正方形ABCD,
∴AD∥BC,∠B=90°,
∴∠DAE=∠AEB,
∵PF⊥AE,
∴∠PFA=90°,
∴∠B=∠PFA,
∴△PFA∽△ABE;
(2)解:当△PFE∽△ABE时,
∴∠PEF=∠AEB,,
由题意可得:,
∴,
∴PF=2EF,
∵AE2=AB2+BE2,
∴,
∴∠DAE=∠AEB,
∴∠PAE=∠PEA,
∴PA=PE,
∵PF⊥AE,
∴,
∴,
∴;
当△EFP∽△ABE时,如图2,
∴∠PEF=∠EAB,
∴AB∥PE,
∴∠PEB=180°-∠B=90°,
∴四边形ABEP是矩形,
∴AP=BE=2,
当PA为5或2时,能使得△PEF与△ABE相似.
22、(1)证明:在菱形ABCD中,点E在边BC上,AC菱形的对角线,
∴AB=CD=CB=AD,∠DCP=∠BCP,AD∥BC,CD∥AB,
∴∠CDP=∠F,
在△DCP与△BCP中,
,
∴△DCP≌△BCP(SAS),
∴∠CDP=∠CBP,
∴∠CBP=∠F,
又∵∠BPE=∠FPB,
∴△BPE∽△FPB,
∴,
∴PB2=PE PF;
(2)解:由(1)得:△BPE∽△FPB,
∴,
∵AD=6,PB=2PE,
∴,
∴BF=2BE,
∵AD∥BC,
∴△BEF∽△ADF,
∴,
∴,
∴AF=2AD,
∵AB=AD=6,
∴AF=2AD=12,
∴BF=AF-AB=6.
同课章节目录
