浙教版数学九年级上册 第3章 圆的基本性质 单元测试(含答案)
文档属性
| 名称 | 浙教版数学九年级上册 第3章 圆的基本性质 单元测试(含答案) | 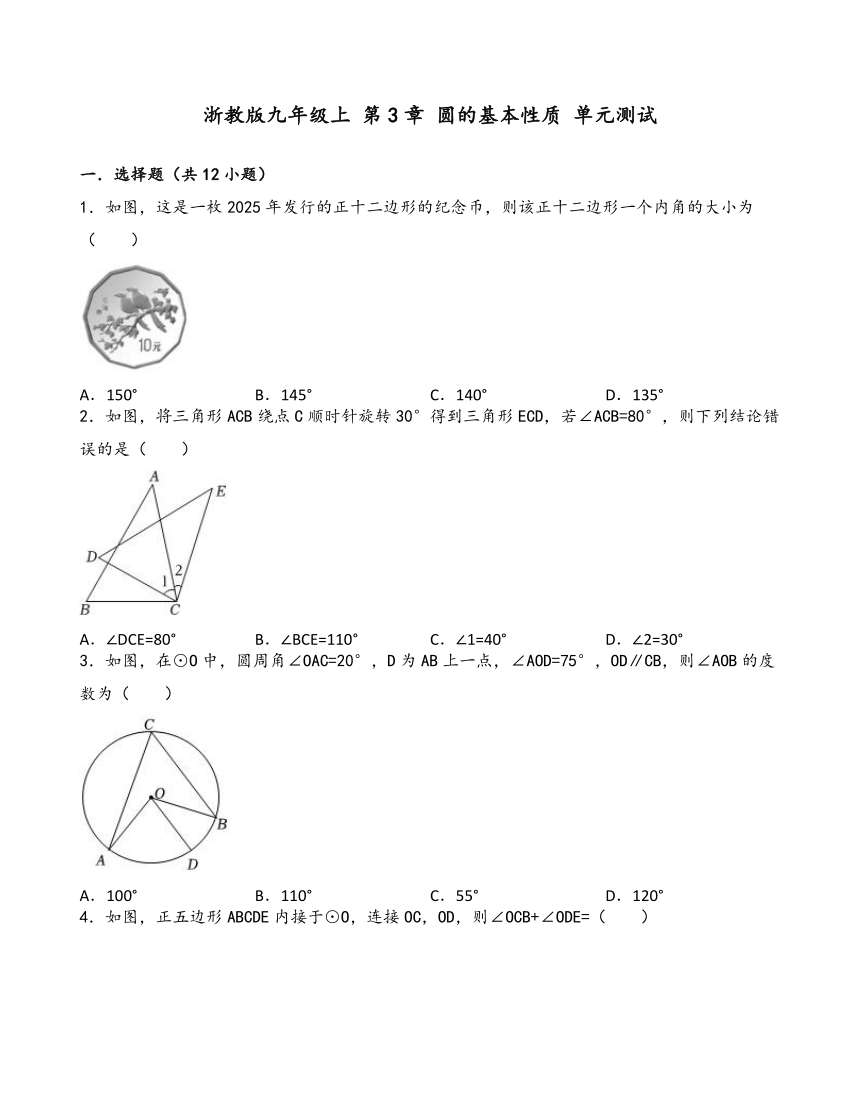 | |
| 格式 | docx | ||
| 文件大小 | 148.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 23:29:01 | ||
图片预览


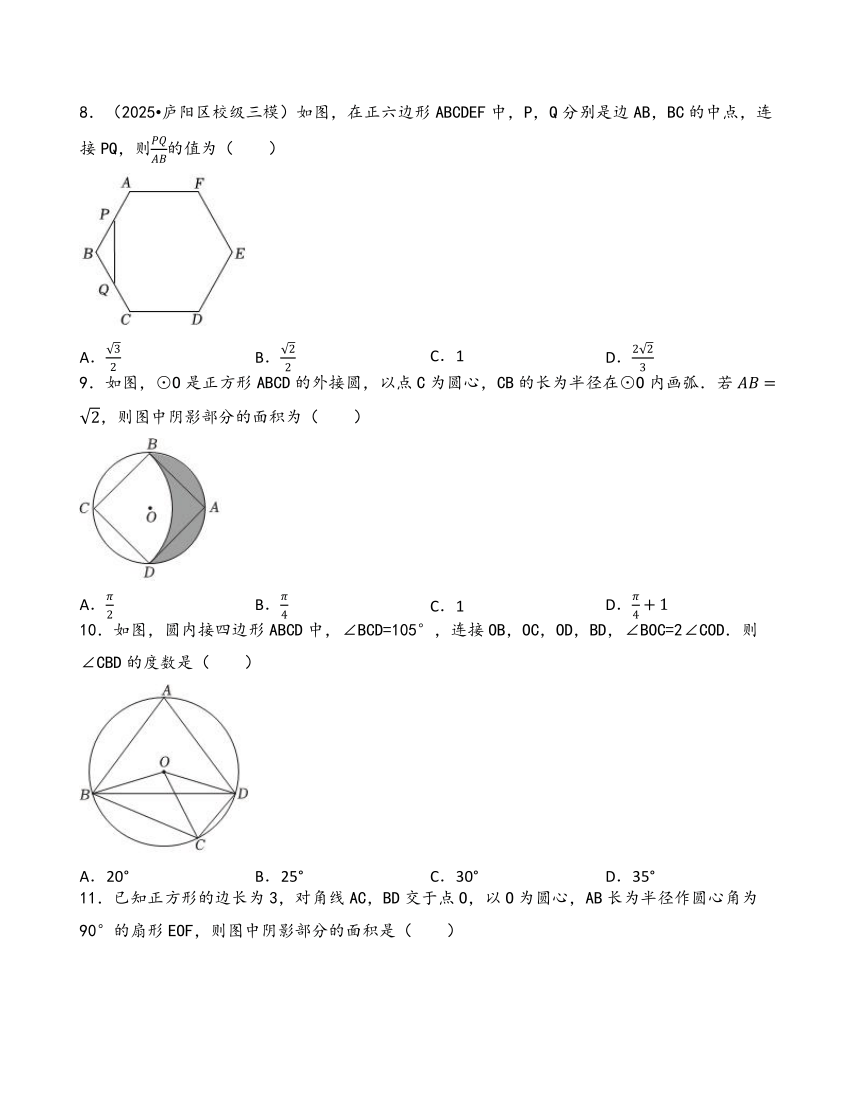

文档简介
浙教版九年级上 第3章 圆的基本性质 单元测试
一.选择题(共12小题)
1.如图,这是一枚2025年发行的正十二边形的纪念币,则该正十二边形一个内角的大小为( )
A.150° B.145° C.140° D.135°
2.如图,将三角形ACB绕点C顺时针旋转30°得到三角形ECD,若∠ACB=80°,则下列结论错误的是( )
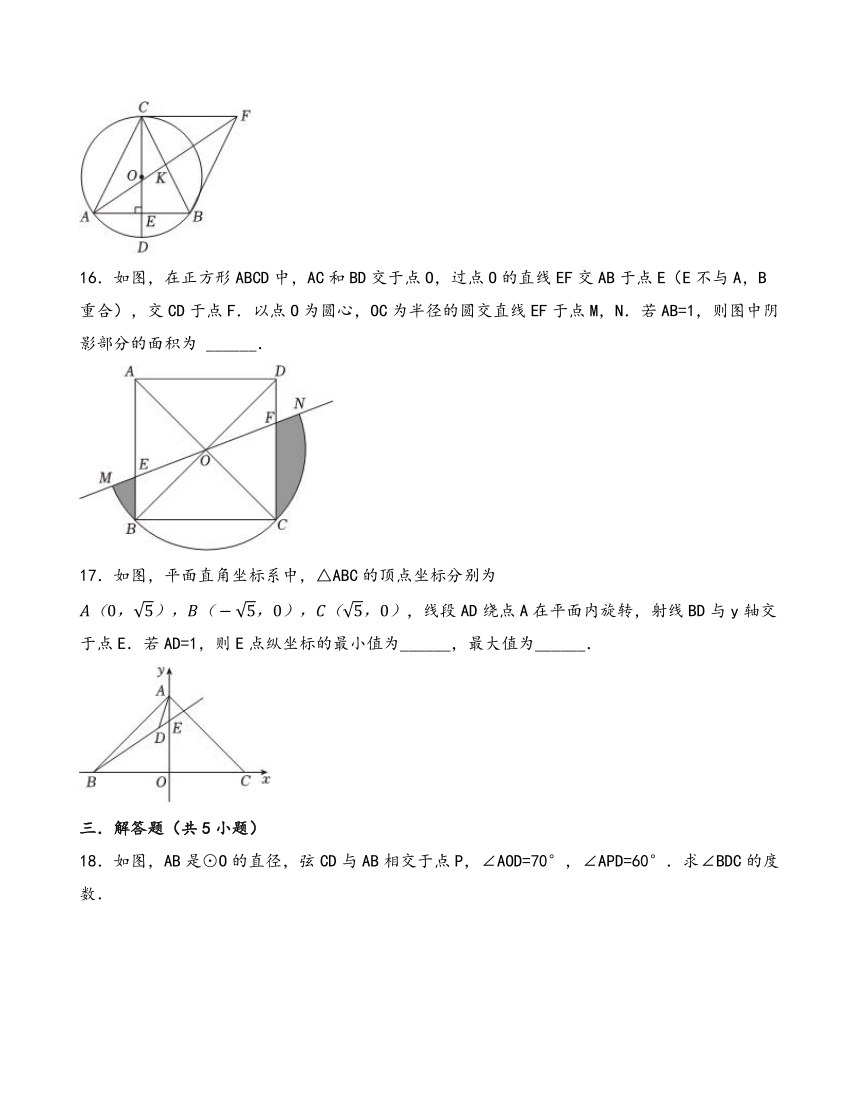
A.∠DCE=80° B.∠BCE=110° C.∠1=40° D.∠2=30°
3.如图,在⊙O中,圆周角∠OAC=20°,D为AB上一点,∠AOD=75°,OD∥CB,则∠AOB的度数为( )
A.100° B.110° C.55° D.120°
4.如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠OCB+∠ODE=( )
A.72° B.98° C.102° D.108°
5.如图,BC是⊙O的弦,点A是圆上一点,OA⊥BC于点D.若OA=5,BC=8,则AD的长是( )
A.3 B.2 C. D.
6.如图,线段AE是⊙O的直径,线段BC是⊙O的弦,且AE⊥BC,点D是⊙O上一点,AD、BC交于点G,BD=GD,若∠DAE=α,则∠DCB一定等于( )
A.2α B.90°+α C.180°-α D.270°-3α
7.如图,在Rt△AOB中,∠AOB=90°,OA=4,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以点O,E为圆心,以OA,ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是( )
A.2π B.π+5 C.10+4π D.10-π
8.(2025 庐阳区校级三模)如图,在正六边形ABCDEF中,P,Q分别是边AB,BC的中点,连接PQ,则的值为( )
A. B. C.1 D.
9.如图,⊙O是正方形ABCD的外接圆,以点C为圆心,CB的长为半径在⊙O内画弧.若,则图中阴影部分的面积为( )
A. B. C.1 D.
10.如图,圆内接四边形ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD.则∠CBD的度数是( )
A.20° B.25° C.30° D.35°
11.已知正方形的边长为3,对角线AC,BD交于点O,以O为圆心,AB长为半径作圆心角为90°的扇形EOF,则图中阴影部分的面积是( )
A. B. C. D.
12.如图,在平面直角坐标系中,已知A(5,5),B(8,0),点P在以A为圆心,2为半径的圆上,P关于B的对称点为Q.连接OP,将OP绕点O逆时针旋转90°得到OR.连接RQ.则RQ的最小值是( )
A.14 B.15 C. D.
二.填空题(共5小题)
13.若60°圆心角所对的弧长是5π,则此弧所在圆的半径是______.
14.两个半径相等的半圆按如图所示放置,半圆O′的圆心落在半圆O的圆弧上,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为1,则阴影部分的面积是______.
15.如图,⊙O的直径CD=10,弦AB=8,且CD⊥AB于点E,连接AC,以AC,AB为边作平行四边形ABFC,连接AF,BC交于点K,则AK= ______.
16.如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为 ______.
17.如图,平面直角坐标系中,△ABC的顶点坐标分别为,线段AD绕点A在平面内旋转,射线BD与y轴交于点E.若AD=1,则E点纵坐标的最小值为______,最大值为______.
三.解答题(共5小题)
18.如图,AB是⊙O的直径,弦CD与AB相交于点P,∠AOD=70°,∠APD=60°.求∠BDC的度数.
19.(2025 长沙模拟)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转得到△ADE,使得A,C,D三点共线,延长BC交ED于点F,连接FA.
(1)求证:EF=CF;
(2)若EF=3,BC=8,求AB的长.
20.如图,C是以AB为直径的⊙O上的任意一点,AD平分∠CAB交⊙O于点D,连接OD,过点D作DE⊥AC交AC的延长线于点E,延长AB交ED的延长线于点F.
(1)求证:OD∥AE.
(2)若DF=4,BF=2,求AC的长.
21.如图,四边形ABCD内接于⊙O,对角线AC是⊙O的直径,且点D为弦AB所对优弧的中点,连接OD,分别延长AD、BC相交于点M.
(1)求证:AC=CM;
(2)若,BC=3,求直径AC的长.
22.问题提出
(1)如图1,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.已知BC=9,∠DEC=75°,⊙O是△BCE的外接圆,AB交⊙O于点F,连接CF,求⊙O的半径.
问题解决
(2)某社区准备设计一个矩形花园,图2是花园的示意图,图中EF,EG,FG,FC是花园内的四条小路,这四条小路将花园分成五个三角形区域,分别用来种植不同种类的花.根据设计要求,∠EGF=∠CFD,∠EFC=90°,DF:DC=1:2,AE=8米.该矩形花园的面积是否存在最大值?若存在,请求出其最大面积;若不存在,请说明理由.
浙教版九年级上 第3章 圆的基本性质 单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、C 3、B 4、D 5、B 6、D 7、D 8、A 9、C 10、B 11、A 12、D
二.填空题(共5小题)
13、15; 14、; 15、; 16、-; 17、;;
三.解答题(共5小题)
18、解:连接AD,
∵AO=DO,
∴∠A=(180°-70°)=55°,
∵AB是⊙O的直径,
∴∠ADB=90°,∴∠B=35°,
∵OD=OB,
∴∠ODB=∠B=35°,
∵∠ODP=∠AOD-∠OPD=10°,
∴∠BDC=25°.
19、(1)证明:∵∠E=∠ACB=∠ACF=90°,AE=AC,
又∵AF=AF,
∴Rt△AEF≌Rt△ACF,
∴EF=CF;
(2)解:∵DE=BC=8,AB=AD,
∴DF=DE-EF=8-3=5,
又∵EF=CF=3,
∴,
设AE=AC=x,
AE2+DE2=AD2,即x2+82=(x+4)2,
∴x=6,
∴AB=AD=AC+AD=6+4=10.
20、(1)证明:∵AD平分∠CAB,
∴∠EAD=∠DAF.
∵OA=OD
∴∠ADO=∠DAF
∴∠ADO=∠EAD.
∴OD∥AE.
(2)解:过点O作OG⊥AC于点G,连接OC.
则∠AGO=∠EGO=90°.
∵AE⊥EF,
∴∠E=90°.
∵OD∥AE,
∴∠ODF=∠E=90°.
设⊙O的半径为r.
∴OA=OB=OD=r
∵BF=2.
∴OF=OB+BF=r+2
∵∠ODF=90°,DF=4,
∴OF2=OD2+DF2,即(r+2)2=r2+42.
∴r=3.
∴OA=OB=OD=3,OF=5
∵OD∥AE
∴,即.
∴
∵∠AGO=∠EGO=90°,∠E=90°,∠ODE=90°,
∴四边形OGED是矩形.
∴.
∵∠AGO=90°,
∴.
∵OA=OC,OG⊥AC.
∴.
21、(1)证明:如图,延长DO,交AB于F,
∵点D为弦AB所对优弧的中点,
∴DF⊥AB,
∵AC是⊙O的直径,
∴∠ABC=90°,
∴MB∥DF,
∴∠M=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠M=∠OAD,
∴AC=CM;
(2)解:设⊙O的半径为R,则AC=CM=2R,
∵BC=3,
∴MB=MC+BC=2R+3,
∵MB∥DF,OA=OC,
∴AD=DM=2,
∴AM=4,
在Rt△ABM中,AB2=AM2-BM2=(4)2-(2R+3)2,
在Rt△ABC中,AB2=AC2-BC2=(2R)2-32,
∴(4)2-(2R+3)2=(2R)2-32,
解得:R1=,R2=-4(舍去),
∴AC=5.
22、解:(1)∵四边形ABCD是矩形,
∴BC=AD=9,∠BCD=∠ABC=∠ADC=90°,AD∥BC,
∴∠BCE=∠DEC=75°,
∵BE平分∠ABC,
∴,
在△BCE中,∠BEC=180°-∠CBE-∠BCE=60°,
∵,
∴∠BFC=∠BEC=60°,
∵∠CBF=90°,
∴CF是⊙O的直径,
∵,
∴⊙O的半径长是;
(2)作△GEF的外接圆O,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCF=∠CFD,
∵∠EGF=∠CFD,
∴∠EGF=∠BCF,
∵,
∴设CD=2x,则DF=x,
∴,
∴,
∵∠BAD=∠ADC=90°,
∴∠CFD+∠DCF=90°,
∵∠CFE=90°,
∴∠DFC+∠AFE=90°,
∴∠AFE=∠DCF,
∴△AEF∽△DFC,
∴,
∴,
∴AF=2AE=16,
∴,
同理(1)得,
⊙O的直径=,
作OH∥AB,交AD于W,过H作⊙O的切线,交AB于M,延长FC交MH于N,作NR⊥AD于点R,
从而得出矩形ABCD的面积最大值是矩形AMNR的面积,
过点O作PT⊥EF交EF于Q,交AD于P,连接OF,
∴,
∴,
∴,
∴∠OFQ=∠AFE,
∵∠FQP=∠FQO=90°,FQ=FQ,
在△PFQ和△OFQ中,
,
∴△PFQ≌△OFQ(ASA),
∴PF=OF=10,
∵,
∴,
∴WH=OH+OW=10+8=18,
∴RN=WH=18,
∴,
∴AR=AF+FR=16+9=25,
∴,
即矩形ABCD面积的最大值是450m2.
一.选择题(共12小题)
1.如图,这是一枚2025年发行的正十二边形的纪念币,则该正十二边形一个内角的大小为( )
A.150° B.145° C.140° D.135°
2.如图,将三角形ACB绕点C顺时针旋转30°得到三角形ECD,若∠ACB=80°,则下列结论错误的是( )
A.∠DCE=80° B.∠BCE=110° C.∠1=40° D.∠2=30°
3.如图,在⊙O中,圆周角∠OAC=20°,D为AB上一点,∠AOD=75°,OD∥CB,则∠AOB的度数为( )
A.100° B.110° C.55° D.120°
4.如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠OCB+∠ODE=( )
A.72° B.98° C.102° D.108°
5.如图,BC是⊙O的弦,点A是圆上一点,OA⊥BC于点D.若OA=5,BC=8,则AD的长是( )
A.3 B.2 C. D.
6.如图,线段AE是⊙O的直径,线段BC是⊙O的弦,且AE⊥BC,点D是⊙O上一点,AD、BC交于点G,BD=GD,若∠DAE=α,则∠DCB一定等于( )
A.2α B.90°+α C.180°-α D.270°-3α
7.如图,在Rt△AOB中,∠AOB=90°,OA=4,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以点O,E为圆心,以OA,ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是( )
A.2π B.π+5 C.10+4π D.10-π
8.(2025 庐阳区校级三模)如图,在正六边形ABCDEF中,P,Q分别是边AB,BC的中点,连接PQ,则的值为( )
A. B. C.1 D.
9.如图,⊙O是正方形ABCD的外接圆,以点C为圆心,CB的长为半径在⊙O内画弧.若,则图中阴影部分的面积为( )
A. B. C.1 D.
10.如图,圆内接四边形ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD.则∠CBD的度数是( )
A.20° B.25° C.30° D.35°
11.已知正方形的边长为3,对角线AC,BD交于点O,以O为圆心,AB长为半径作圆心角为90°的扇形EOF,则图中阴影部分的面积是( )
A. B. C. D.
12.如图,在平面直角坐标系中,已知A(5,5),B(8,0),点P在以A为圆心,2为半径的圆上,P关于B的对称点为Q.连接OP,将OP绕点O逆时针旋转90°得到OR.连接RQ.则RQ的最小值是( )
A.14 B.15 C. D.
二.填空题(共5小题)
13.若60°圆心角所对的弧长是5π,则此弧所在圆的半径是______.
14.两个半径相等的半圆按如图所示放置,半圆O′的圆心落在半圆O的圆弧上,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为1,则阴影部分的面积是______.
15.如图,⊙O的直径CD=10,弦AB=8,且CD⊥AB于点E,连接AC,以AC,AB为边作平行四边形ABFC,连接AF,BC交于点K,则AK= ______.
16.如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为 ______.
17.如图,平面直角坐标系中,△ABC的顶点坐标分别为,线段AD绕点A在平面内旋转,射线BD与y轴交于点E.若AD=1,则E点纵坐标的最小值为______,最大值为______.
三.解答题(共5小题)
18.如图,AB是⊙O的直径,弦CD与AB相交于点P,∠AOD=70°,∠APD=60°.求∠BDC的度数.
19.(2025 长沙模拟)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转得到△ADE,使得A,C,D三点共线,延长BC交ED于点F,连接FA.
(1)求证:EF=CF;
(2)若EF=3,BC=8,求AB的长.
20.如图,C是以AB为直径的⊙O上的任意一点,AD平分∠CAB交⊙O于点D,连接OD,过点D作DE⊥AC交AC的延长线于点E,延长AB交ED的延长线于点F.
(1)求证:OD∥AE.
(2)若DF=4,BF=2,求AC的长.
21.如图,四边形ABCD内接于⊙O,对角线AC是⊙O的直径,且点D为弦AB所对优弧的中点,连接OD,分别延长AD、BC相交于点M.
(1)求证:AC=CM;
(2)若,BC=3,求直径AC的长.
22.问题提出
(1)如图1,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.已知BC=9,∠DEC=75°,⊙O是△BCE的外接圆,AB交⊙O于点F,连接CF,求⊙O的半径.
问题解决
(2)某社区准备设计一个矩形花园,图2是花园的示意图,图中EF,EG,FG,FC是花园内的四条小路,这四条小路将花园分成五个三角形区域,分别用来种植不同种类的花.根据设计要求,∠EGF=∠CFD,∠EFC=90°,DF:DC=1:2,AE=8米.该矩形花园的面积是否存在最大值?若存在,请求出其最大面积;若不存在,请说明理由.
浙教版九年级上 第3章 圆的基本性质 单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、C 3、B 4、D 5、B 6、D 7、D 8、A 9、C 10、B 11、A 12、D
二.填空题(共5小题)
13、15; 14、; 15、; 16、-; 17、;;
三.解答题(共5小题)
18、解:连接AD,
∵AO=DO,
∴∠A=(180°-70°)=55°,
∵AB是⊙O的直径,
∴∠ADB=90°,∴∠B=35°,
∵OD=OB,
∴∠ODB=∠B=35°,
∵∠ODP=∠AOD-∠OPD=10°,
∴∠BDC=25°.
19、(1)证明:∵∠E=∠ACB=∠ACF=90°,AE=AC,
又∵AF=AF,
∴Rt△AEF≌Rt△ACF,
∴EF=CF;
(2)解:∵DE=BC=8,AB=AD,
∴DF=DE-EF=8-3=5,
又∵EF=CF=3,
∴,
设AE=AC=x,
AE2+DE2=AD2,即x2+82=(x+4)2,
∴x=6,
∴AB=AD=AC+AD=6+4=10.
20、(1)证明:∵AD平分∠CAB,
∴∠EAD=∠DAF.
∵OA=OD
∴∠ADO=∠DAF
∴∠ADO=∠EAD.
∴OD∥AE.
(2)解:过点O作OG⊥AC于点G,连接OC.
则∠AGO=∠EGO=90°.
∵AE⊥EF,
∴∠E=90°.
∵OD∥AE,
∴∠ODF=∠E=90°.
设⊙O的半径为r.
∴OA=OB=OD=r
∵BF=2.
∴OF=OB+BF=r+2
∵∠ODF=90°,DF=4,
∴OF2=OD2+DF2,即(r+2)2=r2+42.
∴r=3.
∴OA=OB=OD=3,OF=5
∵OD∥AE
∴,即.
∴
∵∠AGO=∠EGO=90°,∠E=90°,∠ODE=90°,
∴四边形OGED是矩形.
∴.
∵∠AGO=90°,
∴.
∵OA=OC,OG⊥AC.
∴.
21、(1)证明:如图,延长DO,交AB于F,
∵点D为弦AB所对优弧的中点,
∴DF⊥AB,
∵AC是⊙O的直径,
∴∠ABC=90°,
∴MB∥DF,
∴∠M=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠M=∠OAD,
∴AC=CM;
(2)解:设⊙O的半径为R,则AC=CM=2R,
∵BC=3,
∴MB=MC+BC=2R+3,
∵MB∥DF,OA=OC,
∴AD=DM=2,
∴AM=4,
在Rt△ABM中,AB2=AM2-BM2=(4)2-(2R+3)2,
在Rt△ABC中,AB2=AC2-BC2=(2R)2-32,
∴(4)2-(2R+3)2=(2R)2-32,
解得:R1=,R2=-4(舍去),
∴AC=5.
22、解:(1)∵四边形ABCD是矩形,
∴BC=AD=9,∠BCD=∠ABC=∠ADC=90°,AD∥BC,
∴∠BCE=∠DEC=75°,
∵BE平分∠ABC,
∴,
在△BCE中,∠BEC=180°-∠CBE-∠BCE=60°,
∵,
∴∠BFC=∠BEC=60°,
∵∠CBF=90°,
∴CF是⊙O的直径,
∵,
∴⊙O的半径长是;
(2)作△GEF的外接圆O,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCF=∠CFD,
∵∠EGF=∠CFD,
∴∠EGF=∠BCF,
∵,
∴设CD=2x,则DF=x,
∴,
∴,
∵∠BAD=∠ADC=90°,
∴∠CFD+∠DCF=90°,
∵∠CFE=90°,
∴∠DFC+∠AFE=90°,
∴∠AFE=∠DCF,
∴△AEF∽△DFC,
∴,
∴,
∴AF=2AE=16,
∴,
同理(1)得,
⊙O的直径=,
作OH∥AB,交AD于W,过H作⊙O的切线,交AB于M,延长FC交MH于N,作NR⊥AD于点R,
从而得出矩形ABCD的面积最大值是矩形AMNR的面积,
过点O作PT⊥EF交EF于Q,交AD于P,连接OF,
∴,
∴,
∴,
∴∠OFQ=∠AFE,
∵∠FQP=∠FQO=90°,FQ=FQ,
在△PFQ和△OFQ中,
,
∴△PFQ≌△OFQ(ASA),
∴PF=OF=10,
∵,
∴,
∴WH=OH+OW=10+8=18,
∴RN=WH=18,
∴,
∴AR=AF+FR=16+9=25,
∴,
即矩形ABCD面积的最大值是450m2.
同课章节目录
