初中数学浙教版九年级下 第2章 直线与圆的位置关系 单元测试(含答案)
文档属性
| 名称 | 初中数学浙教版九年级下 第2章 直线与圆的位置关系 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 10:42:30 | ||
图片预览



文档简介
浙教版九年级下 第2章 直线与圆的位置关系 单元测试
一.选择题(共12小题)
1.若圆心O到直线l的距离等于⊙O的半径,则直线l与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.无法确定
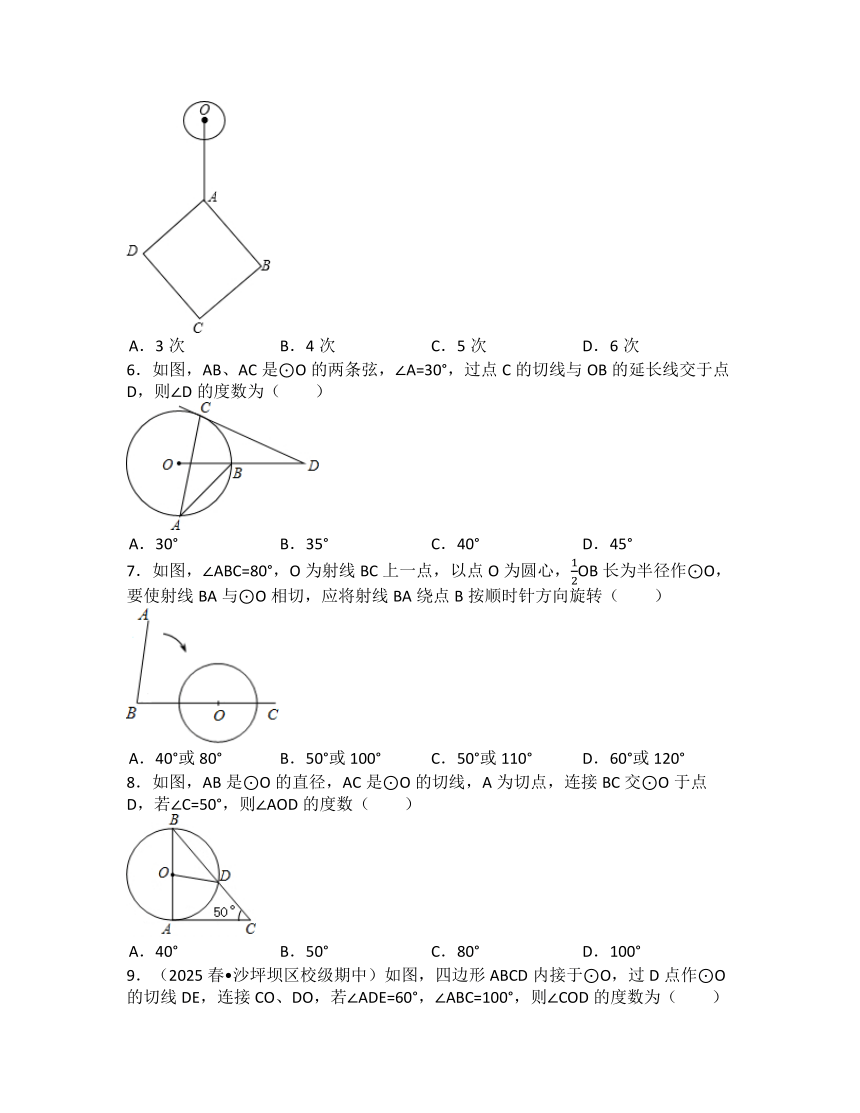
2.如图,已知AB为⊙O的直径,CB切⊙O于B,CD切⊙O于D,交BA的延长线于E,若AB=3,ED=2,则BC的长为( )
A.2 B.3 C.3.5 D.4
3.如图,在Rt△ABC中,∠ACB=90°,以点C为圆心的圆与边AB相切于点D.交边BC于点E,若BC=4,AC=3,则BE的长为( )
A.0.6 B.1.6 C.2.4 D.5
4.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )
A.50° B.57.5° C.60° D.67.5°
5.如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.4次 C.5次 D.6次
6.如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
A.30° B.35° C.40° D.45°
7.如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线BA绕点B按顺时针方向旋转( )
A.40°或80° B.50°或100° C.50°或110° D.60°或120°
8.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,连接BC交⊙O于点D,若∠C=50°,则∠AOD的度数( )
A.40° B.50° C.80° D.100°
9.(2025春 沙坪坝区校级期中)如图,四边形ABCD内接于⊙O,过D点作⊙O的切线DE,连接CO、DO,若∠ADE=60°,∠ABC=100°,则∠COD的度数为( )
A.65° B.70° C.75° D.80°
10.如图,在Rt△ABC中,∠C=90°,BC=3,AC=6,点O,D,E是AB边上的点,以点O为圆心,DE长为直径的半圆O与AC相切于点M,与BC相切于点N,则图中阴影部分的面积为( )
A.5 B.9-2π C.9-π D.5-π
11.如图,矩形ABCD中,AB=4,BC=6,以A为圆心,2为半径作⊙A.动点P在线段BC上(可以与B和C重合),连接AP,与⊙A的交点为点E.连接DE.下列结论错误的是( )
A.PE+PD的最小值是8
B.若DE是⊙A的切线,则
C.△DPE面积的最大值为
D.PA2+PC2的最小值是32
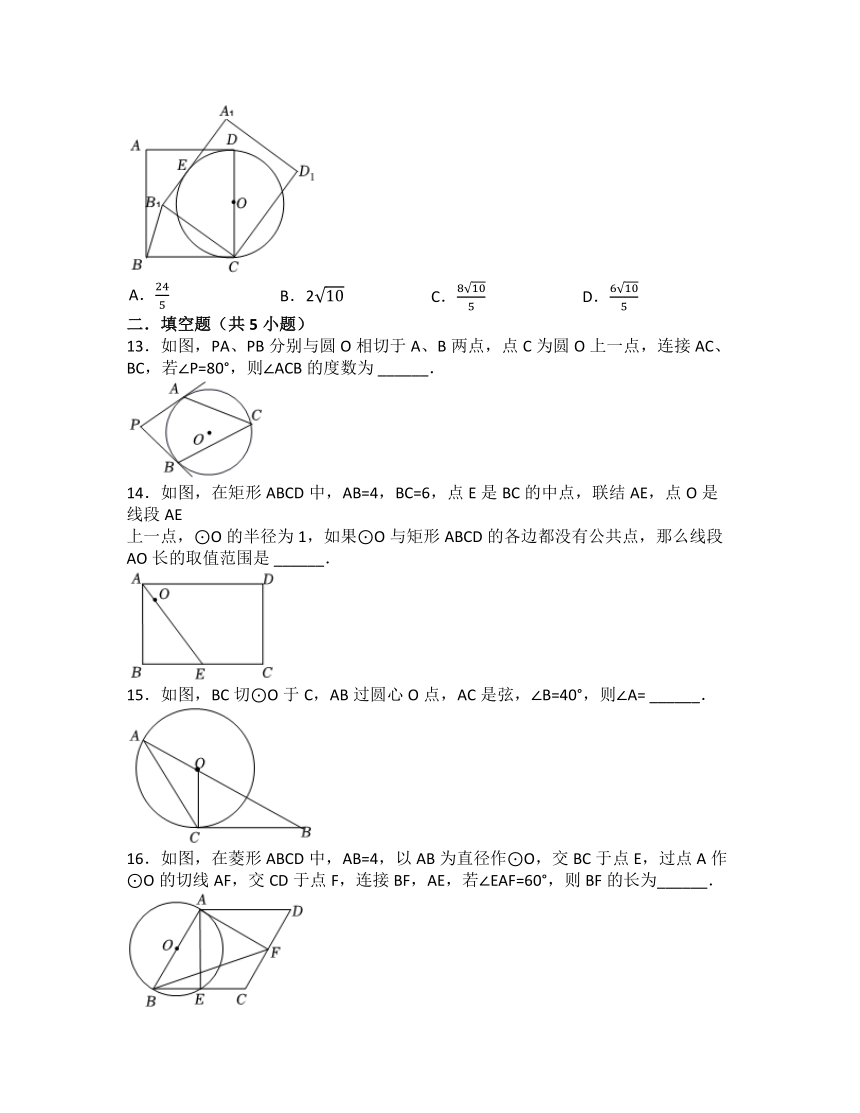
12.如图,在矩形ABCD中AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A1B1C1D1的边A1B1与⊙O相切于点E,则BB1的长为( )
A. B.2 C. D.
二.填空题(共5小题)
13.如图,PA、PB分别与圆O相切于A、B两点,点C为圆O上一点,连接AC、BC,若∠P=80°,则∠ACB的度数为 ______.
14.如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,联结AE,点O是线段AE
上一点,⊙O的半径为1,如果⊙O与矩形ABCD的各边都没有公共点,那么线段AO长的取值范围是 ______.
15.如图,BC切⊙O于C,AB过圆心O点,AC是弦,∠B=40°,则∠A= ______.
16.如图,在菱形ABCD中,AB=4,以AB为直径作⊙O,交BC于点E,过点A作⊙O的切线AF,交CD于点F,连接BF,AE,若∠EAF=60°,则BF的长为______.
17.如图,在平面直角坐标系xOy中,与y轴相切的⊙M与x轴交于A、B两点,AC为⊙M直径,AC=10,AB=6,连接BC,点P为劣弧上点,点Q为线段AB上点,且MP⊥MQ,MP与BC交于点N.则当NQ平分∠MNB时,点P坐标是______.
三.解答题(共5小题)
18.(2025 平谷区一模)如图,AB为⊙O的直径,点C为⊙O外一点,AB=BC,连接AC交⊙O于点D,连接OD,过B作⊙O的切线交DO的延长线于点E.
(1)求证:OD∥BC;
(2)若BC=10,AC=4,求BE的长.
19.如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
20.如图,以△DCE的边DC为直径作⊙O交DE于点A,连接AO并延长交⊙O于点B,连接AC、BC,且∠CED=∠CAB.
(1)求证:CE是⊙O的切线;
(2)若,,求线段CE的长(保留根号).
21.如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:FC=FB;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.
22.如图1,在四边形ABCD中,AD=CD=6,∠B=60°,以AB为直径所作的⊙O经过点C,且与AD相切于A点,连接AC.
(1)求证:CD是⊙O的切线;
(2)⊙E是△ACD的外接圆,不与A、D重合的点F在⊙E的劣弧AD上运动(如图2所示).若点P、Q分别为线段AC、CD上的动点(不与端点重合),当点F运动到每一个确定的位置时,△FPQ的周长有最小值m,随着点F的运动,m的值也随之变化,求m的最大值.
浙教版九年级下 第2章 直线与圆的位置关系 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、B 3、B 4、D 5、B 6、A 7、C 8、C 9、D 10、D 11、D 12、C
二.填空题(共5小题)
13、50°; 14、<AO<; 15、25°; 16、; 17、(,);
三.解答题(共5小题)
18、(1)证明:∵AB=BC,
∴∠A=∠C,
∵OD=OA,
∴∠A=∠ODA,
∴∠ODA=∠C,
∴OD∥BC.
(2)解:连接BD,作DF⊥AB于点F,则∠OFD=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=BC=10,AC=4,且BD⊥AC,
∴OD=OB=AB=5,AD=CD=AC=2,
∴BD===4,
∵S△ABD=×10DF=×2×4,
∴DF=4,
∴OF===3,
∵BE与⊙O相切于点B,
∴BE⊥OB于点B,
∴∠OBE=90°,
∵∠BOE=∠FOD,
∴=tan∠BOE=tan∠FOD==,
∴BE=OB=×5=,
∴BE的长为.
19、解:(1)PB与⊙O相切
理由如下:∵AB是⊙O的直径,
∴AC⊥BD,
又AB=AD,
∴AP是线段BD的垂直平分线,
∴PB=PD,
在△ABP和△ADP中,
,
∴△ABP≌△ADP(SSS)
∴∠ABP=∠ADP=90°,
∴PB与⊙O相切;
(2)∵△ABP≌△ADP,
∴∠BAC=∠DAC,
∴=,
∴BC=CE=3,
∵AB=AD,AC⊥BD,
∴BC=CD=3,
由切割线定理得,DC DB=DE DA,即3×6=DE×(DE+7),
解得,DE=2,
∴DA=2+7=9,
∴AB=AD=9,
∴⊙O的半径为4.5.
20、(1)证明:∵∠CAD=∠E+∠ECA,∠CAD=∠CAB+∠BAD,
∴∠ECA=∠BAD,
∵OA=OD,
∴∠BAD=∠D,
∴∠ECA=∠D,
∵CD为直径,
∴∠CAD=90°,
∴∠D+∠ACD=90°,
∴∠ECA+∠ACD=90°,
∴∠ECO=90°,
∴EC⊥CO,
∵CO为半径,
∴CE是⊙O的切线;
(2)解:∵∠B=∠D,
∴tanB=tanD=,
设CE=3x,DC=5x,
∵CE2+CD2=DE2,
∴(3x,
∴,
∴CE=.
21、(1)证明:连接OC,BC,
∵CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴=,=,
∴=,
∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF.
(2)证明∵BF切⊙O于B,
∴∠FBC=∠CAB,
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC,
∴∠FCB=∠CAB,
∵∠ACB=90°,
∴∠ACO+∠BCO=90°,
∴∠FCB+∠BCO=90°,
即OC⊥CG,
∴CG是⊙O切线,
(3)解:∵BF=CF=DF(已证),EF=BF=2,
∴EF=FC,
∴∠FCE=∠FEC,
∵∠AHE=∠CHG=90°,
∴∠FAH+∠AEH=90°,∠G+∠GCH=90°,
∵∠AEH=∠CEF,
∴∠G=∠FAG,
∴AF=FG,
∵FB⊥AG,
∴AB=BG,
∵GBA是⊙O割线,AB=BG,FB=FE=2,
∴由切割线定理得:(2+FG)2=BG×AG=2BG2,
在Rt△BFG中,由勾股定理得:BG2=FG2-BF2,
∴FG2-4FG-12=0,
解得:FG=6,FG=-2(舍去),
由勾股定理得:
AB=BG==4,
∴⊙O的半径是2.
解法二:过点F作FJ⊥CE于J.
∵FC=FE,FJ⊥CE,
∴CJ=JE,
∵CE=EH,
∴EH=2JE,
∵FJ∥AH,
∴△FJE∽△AHE,
∴==,
∴AE=2EF=4,
∴AF=AE+EF=6,
∵BF=2,∠ABF=90°,
∴AB===4,
∴⊙O的半径为2.
22、(1)证明:如图1,连接CO,
∵AB是圆O的直径,
∴∠ACB=90°,
∵∠B=60°,
∴∠CAB=30°,
∵AD与圆O相切于A点,
∴∠DAB=90°,
∵∠CAB=30°,
∴∠CAD=60°,
∵AC=CD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠OCD=90°,
∴CD是圆的切线;
(2)解:如图2,作F点关于CD的对称点M,作F点关于AC的对称点N,连接MQ,NP,
∴FQ=MQ,PN=FP,
∴△PQF的周长=FQ+FP+PQ=MQ+PN+PQ≥MN,
∴当M、Q、P、N四点共线时,△PQF的周长有最小值,
连接CN,CM,FM,FN,
∵∠ACD=60°,F点在⊙E的劣弧AD上,
∴∠MFN=120°,
连接CF,
由对称性可知,CF=CM,CF=CN,
∴CM=CN,
∵∠MFC=∠FMC,∠CFN=∠FNC,
∴∠FMC+∠FNC=120°,
∵FM=FN,CM=CN,
∴∠CMN+∠CNM=60°,
∴∠MNC=120°,∠CMN=∠CNM=30°,
过点C作CH⊥MN交于H点,
∴NH=CN,MH=CM,
∴MN=CN=CF,
当FC最大时,m的值最大,
当CF为圆E的直径时,CF最大,
如图3,在△ACD中,连接AE延长交CD于G,连接ED,
∵圆E是△ABC的外接圆,
∴AG⊥CD,∠EDC=30°,
∵AD=CD=6,
∴DG=3,
∴DE==6,
∴CF=12,
∴m的最大值为12.
一.选择题(共12小题)
1.若圆心O到直线l的距离等于⊙O的半径,则直线l与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.无法确定
2.如图,已知AB为⊙O的直径,CB切⊙O于B,CD切⊙O于D,交BA的延长线于E,若AB=3,ED=2,则BC的长为( )
A.2 B.3 C.3.5 D.4
3.如图,在Rt△ABC中,∠ACB=90°,以点C为圆心的圆与边AB相切于点D.交边BC于点E,若BC=4,AC=3,则BE的长为( )
A.0.6 B.1.6 C.2.4 D.5
4.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )
A.50° B.57.5° C.60° D.67.5°
5.如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.4次 C.5次 D.6次
6.如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
A.30° B.35° C.40° D.45°
7.如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线BA绕点B按顺时针方向旋转( )
A.40°或80° B.50°或100° C.50°或110° D.60°或120°
8.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,连接BC交⊙O于点D,若∠C=50°,则∠AOD的度数( )
A.40° B.50° C.80° D.100°
9.(2025春 沙坪坝区校级期中)如图,四边形ABCD内接于⊙O,过D点作⊙O的切线DE,连接CO、DO,若∠ADE=60°,∠ABC=100°,则∠COD的度数为( )
A.65° B.70° C.75° D.80°
10.如图,在Rt△ABC中,∠C=90°,BC=3,AC=6,点O,D,E是AB边上的点,以点O为圆心,DE长为直径的半圆O与AC相切于点M,与BC相切于点N,则图中阴影部分的面积为( )
A.5 B.9-2π C.9-π D.5-π
11.如图,矩形ABCD中,AB=4,BC=6,以A为圆心,2为半径作⊙A.动点P在线段BC上(可以与B和C重合),连接AP,与⊙A的交点为点E.连接DE.下列结论错误的是( )
A.PE+PD的最小值是8
B.若DE是⊙A的切线,则
C.△DPE面积的最大值为
D.PA2+PC2的最小值是32
12.如图,在矩形ABCD中AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A1B1C1D1的边A1B1与⊙O相切于点E,则BB1的长为( )
A. B.2 C. D.
二.填空题(共5小题)
13.如图,PA、PB分别与圆O相切于A、B两点,点C为圆O上一点,连接AC、BC,若∠P=80°,则∠ACB的度数为 ______.
14.如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,联结AE,点O是线段AE
上一点,⊙O的半径为1,如果⊙O与矩形ABCD的各边都没有公共点,那么线段AO长的取值范围是 ______.
15.如图,BC切⊙O于C,AB过圆心O点,AC是弦,∠B=40°,则∠A= ______.
16.如图,在菱形ABCD中,AB=4,以AB为直径作⊙O,交BC于点E,过点A作⊙O的切线AF,交CD于点F,连接BF,AE,若∠EAF=60°,则BF的长为______.
17.如图,在平面直角坐标系xOy中,与y轴相切的⊙M与x轴交于A、B两点,AC为⊙M直径,AC=10,AB=6,连接BC,点P为劣弧上点,点Q为线段AB上点,且MP⊥MQ,MP与BC交于点N.则当NQ平分∠MNB时,点P坐标是______.
三.解答题(共5小题)
18.(2025 平谷区一模)如图,AB为⊙O的直径,点C为⊙O外一点,AB=BC,连接AC交⊙O于点D,连接OD,过B作⊙O的切线交DO的延长线于点E.
(1)求证:OD∥BC;
(2)若BC=10,AC=4,求BE的长.
19.如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
20.如图,以△DCE的边DC为直径作⊙O交DE于点A,连接AO并延长交⊙O于点B,连接AC、BC,且∠CED=∠CAB.
(1)求证:CE是⊙O的切线;
(2)若,,求线段CE的长(保留根号).
21.如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:FC=FB;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.
22.如图1,在四边形ABCD中,AD=CD=6,∠B=60°,以AB为直径所作的⊙O经过点C,且与AD相切于A点,连接AC.
(1)求证:CD是⊙O的切线;
(2)⊙E是△ACD的外接圆,不与A、D重合的点F在⊙E的劣弧AD上运动(如图2所示).若点P、Q分别为线段AC、CD上的动点(不与端点重合),当点F运动到每一个确定的位置时,△FPQ的周长有最小值m,随着点F的运动,m的值也随之变化,求m的最大值.
浙教版九年级下 第2章 直线与圆的位置关系 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、B 3、B 4、D 5、B 6、A 7、C 8、C 9、D 10、D 11、D 12、C
二.填空题(共5小题)
13、50°; 14、<AO<; 15、25°; 16、; 17、(,);
三.解答题(共5小题)
18、(1)证明:∵AB=BC,
∴∠A=∠C,
∵OD=OA,
∴∠A=∠ODA,
∴∠ODA=∠C,
∴OD∥BC.
(2)解:连接BD,作DF⊥AB于点F,则∠OFD=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=BC=10,AC=4,且BD⊥AC,
∴OD=OB=AB=5,AD=CD=AC=2,
∴BD===4,
∵S△ABD=×10DF=×2×4,
∴DF=4,
∴OF===3,
∵BE与⊙O相切于点B,
∴BE⊥OB于点B,
∴∠OBE=90°,
∵∠BOE=∠FOD,
∴=tan∠BOE=tan∠FOD==,
∴BE=OB=×5=,
∴BE的长为.
19、解:(1)PB与⊙O相切
理由如下:∵AB是⊙O的直径,
∴AC⊥BD,
又AB=AD,
∴AP是线段BD的垂直平分线,
∴PB=PD,
在△ABP和△ADP中,
,
∴△ABP≌△ADP(SSS)
∴∠ABP=∠ADP=90°,
∴PB与⊙O相切;
(2)∵△ABP≌△ADP,
∴∠BAC=∠DAC,
∴=,
∴BC=CE=3,
∵AB=AD,AC⊥BD,
∴BC=CD=3,
由切割线定理得,DC DB=DE DA,即3×6=DE×(DE+7),
解得,DE=2,
∴DA=2+7=9,
∴AB=AD=9,
∴⊙O的半径为4.5.
20、(1)证明:∵∠CAD=∠E+∠ECA,∠CAD=∠CAB+∠BAD,
∴∠ECA=∠BAD,
∵OA=OD,
∴∠BAD=∠D,
∴∠ECA=∠D,
∵CD为直径,
∴∠CAD=90°,
∴∠D+∠ACD=90°,
∴∠ECA+∠ACD=90°,
∴∠ECO=90°,
∴EC⊥CO,
∵CO为半径,
∴CE是⊙O的切线;
(2)解:∵∠B=∠D,
∴tanB=tanD=,
设CE=3x,DC=5x,
∵CE2+CD2=DE2,
∴(3x,
∴,
∴CE=.
21、(1)证明:连接OC,BC,
∵CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴=,=,
∴=,
∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF.
(2)证明∵BF切⊙O于B,
∴∠FBC=∠CAB,
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC,
∴∠FCB=∠CAB,
∵∠ACB=90°,
∴∠ACO+∠BCO=90°,
∴∠FCB+∠BCO=90°,
即OC⊥CG,
∴CG是⊙O切线,
(3)解:∵BF=CF=DF(已证),EF=BF=2,
∴EF=FC,
∴∠FCE=∠FEC,
∵∠AHE=∠CHG=90°,
∴∠FAH+∠AEH=90°,∠G+∠GCH=90°,
∵∠AEH=∠CEF,
∴∠G=∠FAG,
∴AF=FG,
∵FB⊥AG,
∴AB=BG,
∵GBA是⊙O割线,AB=BG,FB=FE=2,
∴由切割线定理得:(2+FG)2=BG×AG=2BG2,
在Rt△BFG中,由勾股定理得:BG2=FG2-BF2,
∴FG2-4FG-12=0,
解得:FG=6,FG=-2(舍去),
由勾股定理得:
AB=BG==4,
∴⊙O的半径是2.
解法二:过点F作FJ⊥CE于J.
∵FC=FE,FJ⊥CE,
∴CJ=JE,
∵CE=EH,
∴EH=2JE,
∵FJ∥AH,
∴△FJE∽△AHE,
∴==,
∴AE=2EF=4,
∴AF=AE+EF=6,
∵BF=2,∠ABF=90°,
∴AB===4,
∴⊙O的半径为2.
22、(1)证明:如图1,连接CO,
∵AB是圆O的直径,
∴∠ACB=90°,
∵∠B=60°,
∴∠CAB=30°,
∵AD与圆O相切于A点,
∴∠DAB=90°,
∵∠CAB=30°,
∴∠CAD=60°,
∵AC=CD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠OCD=90°,
∴CD是圆的切线;
(2)解:如图2,作F点关于CD的对称点M,作F点关于AC的对称点N,连接MQ,NP,
∴FQ=MQ,PN=FP,
∴△PQF的周长=FQ+FP+PQ=MQ+PN+PQ≥MN,
∴当M、Q、P、N四点共线时,△PQF的周长有最小值,
连接CN,CM,FM,FN,
∵∠ACD=60°,F点在⊙E的劣弧AD上,
∴∠MFN=120°,
连接CF,
由对称性可知,CF=CM,CF=CN,
∴CM=CN,
∵∠MFC=∠FMC,∠CFN=∠FNC,
∴∠FMC+∠FNC=120°,
∵FM=FN,CM=CN,
∴∠CMN+∠CNM=60°,
∴∠MNC=120°,∠CMN=∠CNM=30°,
过点C作CH⊥MN交于H点,
∴NH=CN,MH=CM,
∴MN=CN=CF,
当FC最大时,m的值最大,
当CF为圆E的直径时,CF最大,
如图3,在△ACD中,连接AE延长交CD于G,连接ED,
∵圆E是△ABC的外接圆,
∴AG⊥CD,∠EDC=30°,
∵AD=CD=6,
∴DG=3,
∴DE==6,
∴CF=12,
∴m的最大值为12.
