初中数学浙教版九年级下册第1章《解直角三角形》章节检测卷 (含解析)
文档属性
| 名称 | 初中数学浙教版九年级下册第1章《解直角三角形》章节检测卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 00:00:00 | ||
图片预览

文档简介
第1章《解直角三角形》章节检测卷
一、选择题(本大题共10小题,每小题3分,共30分。)
1.的值等于( )
A. B. C. D.
2.在中,,、、所对的边分别是a、b、c.则下列各式中,正确的是( )
A. B. C. D.
3.如图,广场上空有一个气球A,若,,则气球A离地面的高度的长为( )
A. B. C. D.
4.在中,,则的长为( )
A.8 B.12 C.13 D.18
5.如图所示,已知在中,弦的长为,测得圆周角,则直径为( )
A. B. C. D.
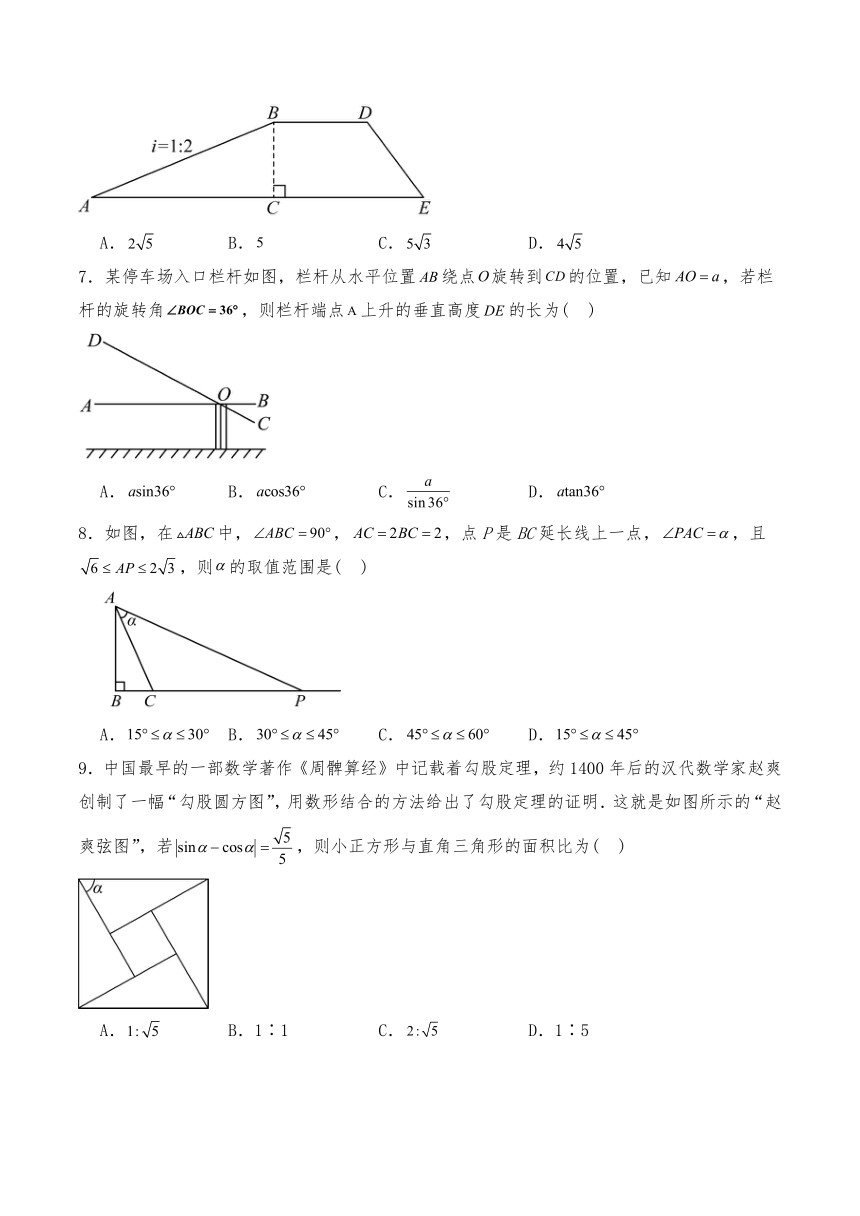
6.如图,大坝横截面的迎水坡的坡比为∶,即∶∶,若坡面长度米,则坡面的水平宽度长为( )
A. B. C. D.
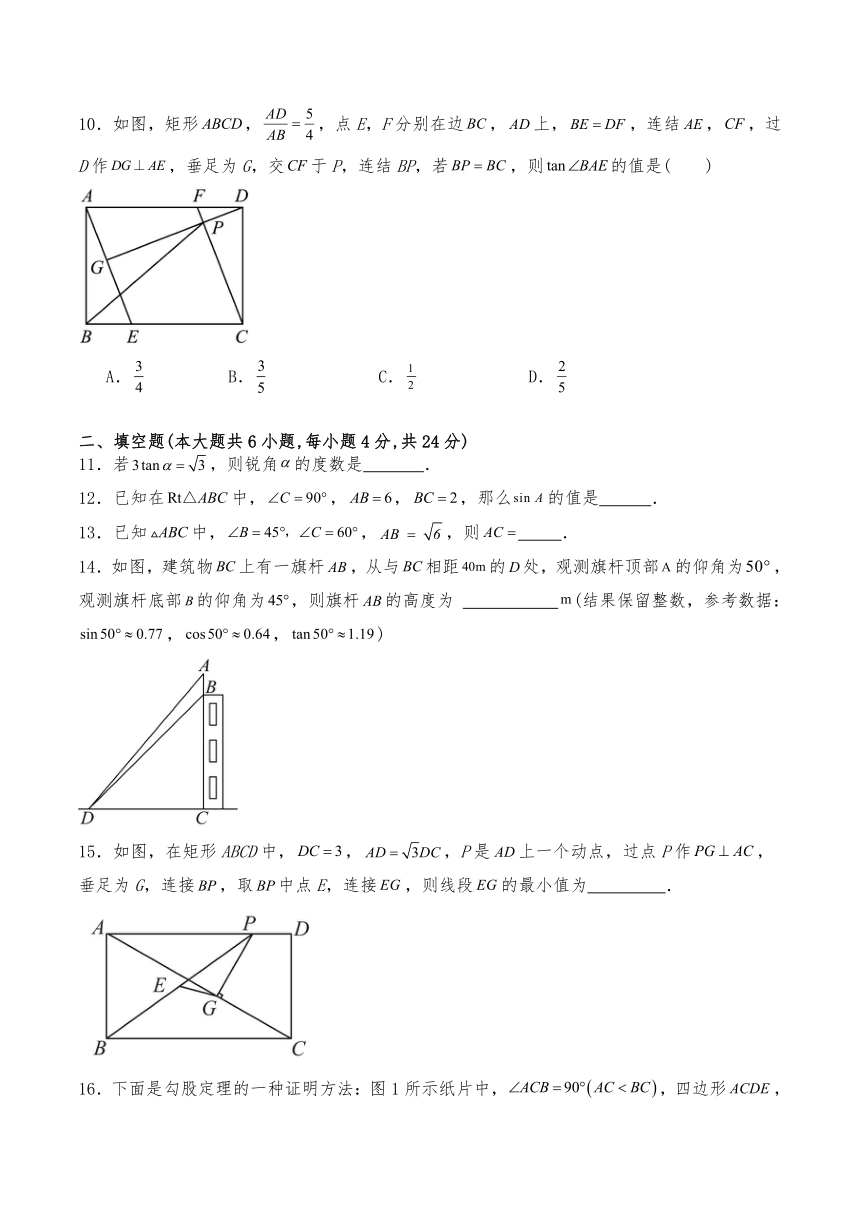
7.某停车场入口栏杆如图,栏杆从水平位置绕点旋转到的位置,已知,若栏杆的旋转角,则栏杆端点上升的垂直高度的长为( )
A. B. C. D.
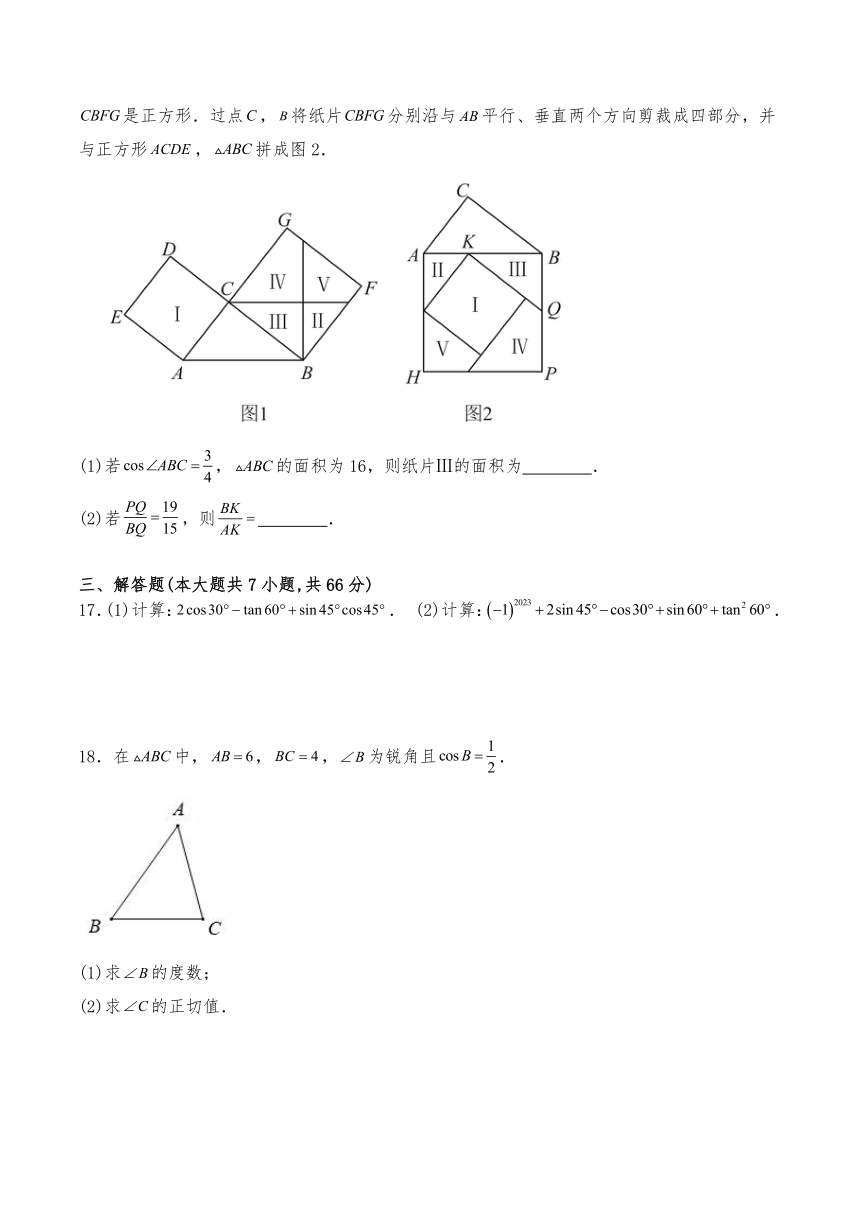
8.如图,在中,,,点P是BC延长线上一点,,且,则的取值范围是( )
A. B. C. D.
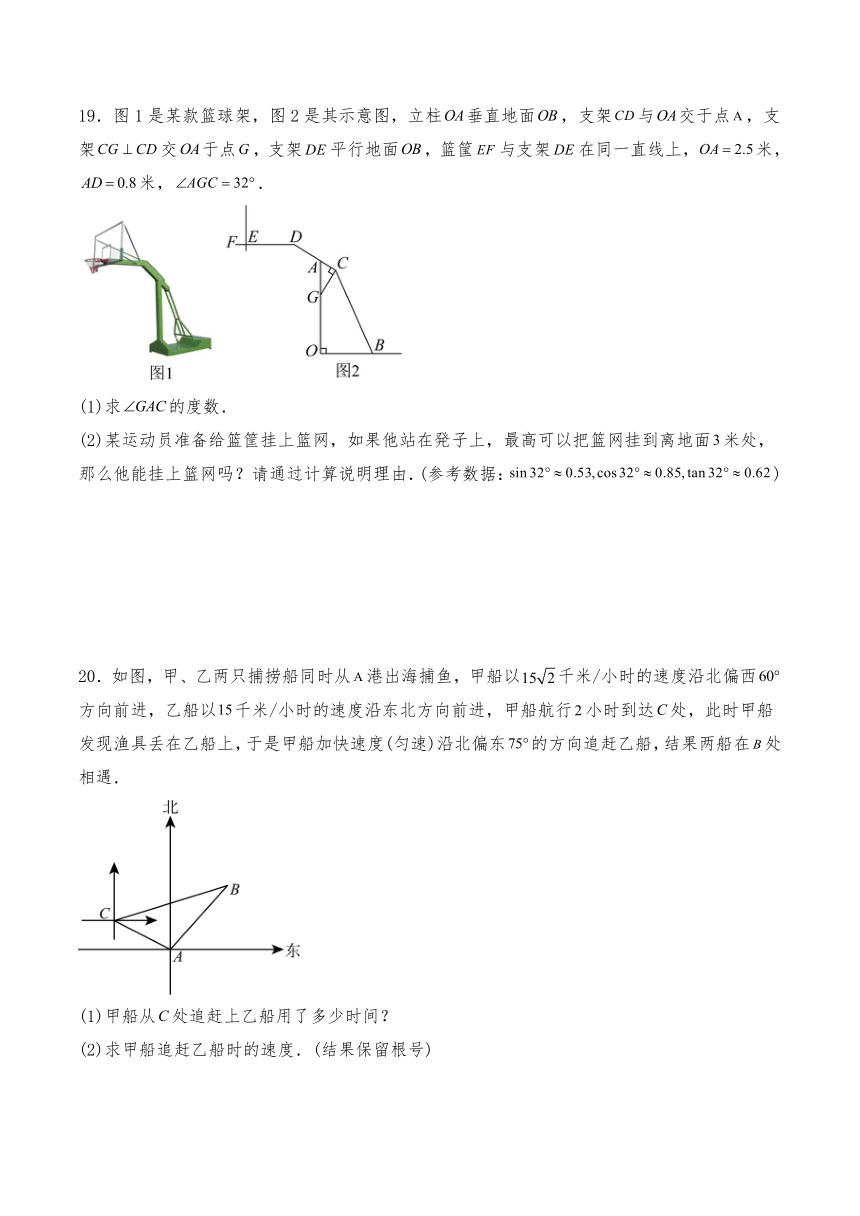
9.中国最早的一部数学著作《周髀算经》中记载着勾股定理,约1400年后的汉代数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的证明.这就是如图所示的“赵爽弦图”,若,则小正方形与直角三角形的面积比为( )
A. B.1∶1 C. D.1∶5
10.如图,矩形,,点E,F分别在边,上,,连结,,过D作,垂足为G,交于P,连结BP,若,则的值是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.若,则锐角的度数是 .
12.已知在中,,,,那么的值是 .
13.已知中,,,则 .
14.如图,建筑物上有一旗杆,从与相距的处,观测旗杆顶部的仰角为,观测旗杆底部的仰角为,则旗杆的高度为 (结果保留整数,参考数据:,,)
15.如图,在矩形ABCD中,,,P是上一个动点,过点P作,垂足为G,连接,取中点E,连接,则线段的最小值为 .
16.下面是勾股定理的一种证明方法:图1所示纸片中,,四边形,是正方形.过点,将纸片分别沿与平行、垂直两个方向剪裁成四部分,并与正方形,拼成图2.
(1)若,的面积为16,则纸片Ⅲ的面积为 .
(2)若,则 .
三、解答题(本大题共7小题,共66分)
17.(1)计算:. (2)计算:.
18.在中,,,为锐角且.
(1)求的度数;
(2)求的正切值.
19.图1是某款篮球架,图2是其示意图,立柱垂直地面,支架与交于点,支架交于点,支架平行地面,篮筺与支架在同一直线上,米,米,.
(1)求的度数.
(2)某运动员准备给篮筐挂上篮网,如果他站在発子上,最高可以把篮网挂到离地面米处,那么他能挂上篮网吗?请通过计算说明理由.(参考数据:)
20.如图,甲、乙两只捕捞船同时从港出海捕鱼,甲船以千米/小时的速度沿北偏西方向前进,乙船以千米/小时的速度沿东北方向前进,甲船航行小时到达处,此时甲船发现渔具丢在乙船上,于是甲船加快速度(匀速)沿北偏东的方向追赶乙船,结果两船在处相遇.
(1)甲船从处追赶上乙船用了多少时间?
(2)求甲船追赶乙船时的速度.(结果保留根号)
21.如图1为放置在水平桌面l上的台灯,底座的高为,长度均为的连杆,与始终在同一平面上.
(1)转动连杆,,使成平角,,如图2,求连杆端点D离桌面l的高度.
(2)将(1)中的连杆再绕点C逆时针旋转,使,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到,参考数据:,)
22.如图,在平行四边形ABCD中,E,F是对角线上的两点(点E在点F左侧),且.
(1)求证:四边形是平行四边形;
(2)当,,时,求的长.
23.如图,矩形中,,点M是的中点,连接.将沿着折叠后得,延长交于E,连接.
(1)求证:平分
(2)求证:.
(3)若,,求的值.
24.如图,四边形内接于,,为直径,为一动点,连结交于点,交于点,连结.
(1)设为,请用表示的度数.
(2)如图1,当时,
①求证:.
②当时,求半径的长.
(3)如图2,当过圆心时,若,直接写出的值(用含的代数式表示.)
参考答案
一、选择题
1.C
【分析】根据特殊角的三角函数值进行解答即可.
【详解】解:,故C正确.
故选:C.
2.C
【分析】根据在直角三角形中,锐角的正弦等于对边比斜边求解即可.
【详解】解:如图,
∴
故选C.
3.B
【分析】由题意可得即可得到气球A离地面的高度的长.
【详解】解:∵,
∴,
∵,
∴,
故选:B
4.C
【分析】在中,,求出,由勾股定理求出的长即可.
【详解】解:在中,∵,
∴,
∴,
故选:C.
5.B
【分析】连接,可证,,由即可求解.
【详解】解:如图,连接,
,
,
∵是直径,
∴,
(),
故选:B.
6.D
【分析】根据坡度的概念得到,根据勾股定理计算即可.
【详解】解:坡面的坡度为:,
,即,
由勾股定理得,,
则,
解得,
故斜坡的水平宽度的长为米.
故选:D.
7.A
【分析】过点D作于E,由题意得米,根据求出答案.
【详解】解:如图,过点D作于E,
由题意得O米,
在中,,,
∴栏杆端点A上升的垂直距离米,
故选:A.
8.A
【分析】根据,,求出,则,求出,分别求出当时,当时的的度数,即可求出的取值范围.
【详解】解:∵,,
∴,
∴,
∴,
当时,
∴,
∴,则;
当时,
∴,
∴,则;
∵,
∴,
故选:A.
9.B
【分析】在中,根据锐角三角函数的定义得出,代入,两边平方得出,由“赵爽弦图”,结合图形可知等于小正方形的边长,那么.再根据,即可求解.
【详解】解:如图.
在中,∵,
∴.
∵,
∴,
∴,
即.
设,则,
∴,
∴.
故选:B.
10.D
【分析】作于点H,交于点I,可证明,得,由等腰三角形的性质得,再证明四边形是矩形,则,由,,得所以,再根据即可得出答案
【详解】解:作于点H,交于点I,
∵于点G,
∴,
∵四边形是矩形,
∴,,
∵,
∴,
∴,
∴四边形是平行四边形,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∵
∴四边形是矩形,
∴
∵,,
∴
∴
∴
∴
故选:D.
二、填空题
11.
【分析】利用特殊角的三角函数值计算即可得到锐角的度数.
【详解】解:∵,
∴,
那么锐角的度数为.
故答案为:.
12.
【分析】画出图形,直接利用正弦函数值的定义进行求解即可.
【详解】
在中,,,
∴.
故答案为:.
13.2
【分析】过点A作交于点D,根据三角形内角和定理,得到,进而得到,再利用勾股定理求得,然后解直角三角形即可求解.
【详解】解:过点A作交于点D,
,
,
,
,
在中,,
,
∵,
∴,
故答案为:2.
14.8
【分析】根据正切的定义,得出,再根据三角形的内角和定理,结合等腰三角形的定义,得出是等腰直角三角形,进而得出,再根据线段之间的数量关系,计算即可得出答案.
【详解】解:由题意得:,,,,
在中,
,
∴,
在中,,
∴是等腰直角三角形,
∴,
∴.
∴旗杆的高度为.
故答案为:8.
15.
【分析】取的中点F,连接,作于H,作于T,设,分别表示出,进而表示出和,进而表示出,进一步得出结果.
【详解】解:如图,取的中点F,连接,作于H,作于T,设,
∵四边形是矩形,
∴,
∴,
∴,
∵,
∴,
∴,
,
∵E是的中点,
∴,
∴,
,
在中,
,
∴当时,的最小值为.
故答案为:
16. 9
【分析】(1)在图1中,过作于,由,可得,,故,而的面积为16,即可得纸片Ⅲ的面积为;
(2)标识字母如图,设,证明,可得,由,有,即,可得或,而,,即可得到答案.
【详解】(1)在图1中,过作于,如图:
,
,
,
,即,
,
,
,即,
,
,
的面积为16,
,
,
,
纸片Ⅲ的面积为;
故答案为:9;
(2)如图:
,
,
设,则,,
,,,
,
,
,,
,
,
,
,
解得或,
当时,,这情况不符合题意,舍去;
当时,,
而,,
.
故答案为:.
三、解答题
17.解:(1)
;
(2)
.
18.解:(1)∵∠B为锐角且,
∴∠B=60°;
(2)作AD⊥BC于D,如图所示:
∵,
∴,
∵,
∴BD=AB=3,
∴AD=,
∵BC=4,BD=3,
∴CD=BC﹣BD=1,
∴tanC===3.
19.(1)解:∵,
∴,
∵,
∴.
(2)该运动员能挂上篮网,理由如下.
如图,延长交于点,
∵,
∴,
又∵,
∴,
在中,,
∴,
∴该运动员能挂上篮网.
20.(1)解:如图,过作于点,作交于点,
∵甲船沿北偏西方向前进,乙船沿东北方向前进,
∴,,,
∴;
∵,
∴,
∵甲船沿北偏东的方向追赶乙船,
∴,
∴,
∴,
∴;
在中,,,
∴,
∴,
∵甲船以千米/小时的速度航行小时到达处,
∴(千米);
在中,,
∴(千米),
∴(千米),
∵,,
∴(千米),
且乙船以千米/小时的速度沿东北方向前进,
故甲船从处追赶上乙船的时间是:(小时).
(2)解:在中,,
∴(千米),
故甲船追赶乙船的速度是(千米/小时).
21.(1)如图2中,作于点O.
根据题意有:,
∵,
∴四边形是矩形,
∴,
∵,
∴,
∴(),
∴();
(2)作于F,于P,于G,于H.
则四边形是矩形,
∵根据(1)求出,,
∴,
∵,
∴,
∴(),(),
∴(),
∴下降高度:().
22.(1)∵,
∴,,
∴
∵四边形是平行四边形,
∴,,
∴,
∴,
∴,
∴四边形是平行四边形.
(2)∵在中,,
∴设,,
∵在中,,
即,
解得或(舍去)
∴,.
由(1)得:四边形是平行四边形,
∴,,
∵,
∴,
∴,
∴,
∴,
设,则,
∴,
解得:或(舍去),
即,
由(1)得,
∴,
∴.
23.(1)证明:∵四边形是矩形,
∴,
由折叠性质可得:,
∵延长交于E,
∴,
∴,
∵点M是的中点,
∴,
由折叠性质可得:,
∴,
∵,
∴,
∴,
∴平分;
(2)证明:由折叠性质可得:,
由(1)得:,
∵,
∴,
∵∠B=90°,
∵,
∴,
∵,
∴;
(3)解:由(2)得:,
∵,
∴,
由(2)得:,
由折叠性质得:,
∴,
∴,
∵,
∴,
∴,
由(1)得:,
∴,
∴,
由折叠性质的:,
∴,
∴,
∴;
24.(1)为直径,
,
又,,
.
,
,
.
(2)①连接.
,,,
,
,.
,
,
又,,
,
,,
.
②过点作,垂足为.
,,
,,
,,
.
由,得.
.
,
,
∵
∴.
由勾股定理得.
(3)解:如图所示,连接交于点,
,,
,
为直径,
.
为中点.
为的中位线,
,.
,
,
,
.
,
,
令,则,,
,,
.
一、选择题(本大题共10小题,每小题3分,共30分。)
1.的值等于( )
A. B. C. D.
2.在中,,、、所对的边分别是a、b、c.则下列各式中,正确的是( )
A. B. C. D.
3.如图,广场上空有一个气球A,若,,则气球A离地面的高度的长为( )
A. B. C. D.
4.在中,,则的长为( )
A.8 B.12 C.13 D.18
5.如图所示,已知在中,弦的长为,测得圆周角,则直径为( )
A. B. C. D.
6.如图,大坝横截面的迎水坡的坡比为∶,即∶∶,若坡面长度米,则坡面的水平宽度长为( )
A. B. C. D.
7.某停车场入口栏杆如图,栏杆从水平位置绕点旋转到的位置,已知,若栏杆的旋转角,则栏杆端点上升的垂直高度的长为( )
A. B. C. D.
8.如图,在中,,,点P是BC延长线上一点,,且,则的取值范围是( )
A. B. C. D.
9.中国最早的一部数学著作《周髀算经》中记载着勾股定理,约1400年后的汉代数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的证明.这就是如图所示的“赵爽弦图”,若,则小正方形与直角三角形的面积比为( )
A. B.1∶1 C. D.1∶5
10.如图,矩形,,点E,F分别在边,上,,连结,,过D作,垂足为G,交于P,连结BP,若,则的值是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.若,则锐角的度数是 .
12.已知在中,,,,那么的值是 .
13.已知中,,,则 .
14.如图,建筑物上有一旗杆,从与相距的处,观测旗杆顶部的仰角为,观测旗杆底部的仰角为,则旗杆的高度为 (结果保留整数,参考数据:,,)
15.如图,在矩形ABCD中,,,P是上一个动点,过点P作,垂足为G,连接,取中点E,连接,则线段的最小值为 .
16.下面是勾股定理的一种证明方法:图1所示纸片中,,四边形,是正方形.过点,将纸片分别沿与平行、垂直两个方向剪裁成四部分,并与正方形,拼成图2.
(1)若,的面积为16,则纸片Ⅲ的面积为 .
(2)若,则 .
三、解答题(本大题共7小题,共66分)
17.(1)计算:. (2)计算:.
18.在中,,,为锐角且.
(1)求的度数;
(2)求的正切值.
19.图1是某款篮球架,图2是其示意图,立柱垂直地面,支架与交于点,支架交于点,支架平行地面,篮筺与支架在同一直线上,米,米,.
(1)求的度数.
(2)某运动员准备给篮筐挂上篮网,如果他站在発子上,最高可以把篮网挂到离地面米处,那么他能挂上篮网吗?请通过计算说明理由.(参考数据:)
20.如图,甲、乙两只捕捞船同时从港出海捕鱼,甲船以千米/小时的速度沿北偏西方向前进,乙船以千米/小时的速度沿东北方向前进,甲船航行小时到达处,此时甲船发现渔具丢在乙船上,于是甲船加快速度(匀速)沿北偏东的方向追赶乙船,结果两船在处相遇.
(1)甲船从处追赶上乙船用了多少时间?
(2)求甲船追赶乙船时的速度.(结果保留根号)
21.如图1为放置在水平桌面l上的台灯,底座的高为,长度均为的连杆,与始终在同一平面上.
(1)转动连杆,,使成平角,,如图2,求连杆端点D离桌面l的高度.
(2)将(1)中的连杆再绕点C逆时针旋转,使,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到,参考数据:,)
22.如图,在平行四边形ABCD中,E,F是对角线上的两点(点E在点F左侧),且.
(1)求证:四边形是平行四边形;
(2)当,,时,求的长.
23.如图,矩形中,,点M是的中点,连接.将沿着折叠后得,延长交于E,连接.
(1)求证:平分
(2)求证:.
(3)若,,求的值.
24.如图,四边形内接于,,为直径,为一动点,连结交于点,交于点,连结.
(1)设为,请用表示的度数.
(2)如图1,当时,
①求证:.
②当时,求半径的长.
(3)如图2,当过圆心时,若,直接写出的值(用含的代数式表示.)
参考答案
一、选择题
1.C
【分析】根据特殊角的三角函数值进行解答即可.
【详解】解:,故C正确.
故选:C.
2.C
【分析】根据在直角三角形中,锐角的正弦等于对边比斜边求解即可.
【详解】解:如图,
∴
故选C.
3.B
【分析】由题意可得即可得到气球A离地面的高度的长.
【详解】解:∵,
∴,
∵,
∴,
故选:B
4.C
【分析】在中,,求出,由勾股定理求出的长即可.
【详解】解:在中,∵,
∴,
∴,
故选:C.
5.B
【分析】连接,可证,,由即可求解.
【详解】解:如图,连接,
,
,
∵是直径,
∴,
(),
故选:B.
6.D
【分析】根据坡度的概念得到,根据勾股定理计算即可.
【详解】解:坡面的坡度为:,
,即,
由勾股定理得,,
则,
解得,
故斜坡的水平宽度的长为米.
故选:D.
7.A
【分析】过点D作于E,由题意得米,根据求出答案.
【详解】解:如图,过点D作于E,
由题意得O米,
在中,,,
∴栏杆端点A上升的垂直距离米,
故选:A.
8.A
【分析】根据,,求出,则,求出,分别求出当时,当时的的度数,即可求出的取值范围.
【详解】解:∵,,
∴,
∴,
∴,
当时,
∴,
∴,则;
当时,
∴,
∴,则;
∵,
∴,
故选:A.
9.B
【分析】在中,根据锐角三角函数的定义得出,代入,两边平方得出,由“赵爽弦图”,结合图形可知等于小正方形的边长,那么.再根据,即可求解.
【详解】解:如图.
在中,∵,
∴.
∵,
∴,
∴,
即.
设,则,
∴,
∴.
故选:B.
10.D
【分析】作于点H,交于点I,可证明,得,由等腰三角形的性质得,再证明四边形是矩形,则,由,,得所以,再根据即可得出答案
【详解】解:作于点H,交于点I,
∵于点G,
∴,
∵四边形是矩形,
∴,,
∵,
∴,
∴,
∴四边形是平行四边形,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∵
∴四边形是矩形,
∴
∵,,
∴
∴
∴
∴
故选:D.
二、填空题
11.
【分析】利用特殊角的三角函数值计算即可得到锐角的度数.
【详解】解:∵,
∴,
那么锐角的度数为.
故答案为:.
12.
【分析】画出图形,直接利用正弦函数值的定义进行求解即可.
【详解】
在中,,,
∴.
故答案为:.
13.2
【分析】过点A作交于点D,根据三角形内角和定理,得到,进而得到,再利用勾股定理求得,然后解直角三角形即可求解.
【详解】解:过点A作交于点D,
,
,
,
,
在中,,
,
∵,
∴,
故答案为:2.
14.8
【分析】根据正切的定义,得出,再根据三角形的内角和定理,结合等腰三角形的定义,得出是等腰直角三角形,进而得出,再根据线段之间的数量关系,计算即可得出答案.
【详解】解:由题意得:,,,,
在中,
,
∴,
在中,,
∴是等腰直角三角形,
∴,
∴.
∴旗杆的高度为.
故答案为:8.
15.
【分析】取的中点F,连接,作于H,作于T,设,分别表示出,进而表示出和,进而表示出,进一步得出结果.
【详解】解:如图,取的中点F,连接,作于H,作于T,设,
∵四边形是矩形,
∴,
∴,
∴,
∵,
∴,
∴,
,
∵E是的中点,
∴,
∴,
,
在中,
,
∴当时,的最小值为.
故答案为:
16. 9
【分析】(1)在图1中,过作于,由,可得,,故,而的面积为16,即可得纸片Ⅲ的面积为;
(2)标识字母如图,设,证明,可得,由,有,即,可得或,而,,即可得到答案.
【详解】(1)在图1中,过作于,如图:
,
,
,
,即,
,
,
,即,
,
,
的面积为16,
,
,
,
纸片Ⅲ的面积为;
故答案为:9;
(2)如图:
,
,
设,则,,
,,,
,
,
,,
,
,
,
,
解得或,
当时,,这情况不符合题意,舍去;
当时,,
而,,
.
故答案为:.
三、解答题
17.解:(1)
;
(2)
.
18.解:(1)∵∠B为锐角且,
∴∠B=60°;
(2)作AD⊥BC于D,如图所示:
∵,
∴,
∵,
∴BD=AB=3,
∴AD=,
∵BC=4,BD=3,
∴CD=BC﹣BD=1,
∴tanC===3.
19.(1)解:∵,
∴,
∵,
∴.
(2)该运动员能挂上篮网,理由如下.
如图,延长交于点,
∵,
∴,
又∵,
∴,
在中,,
∴,
∴该运动员能挂上篮网.
20.(1)解:如图,过作于点,作交于点,
∵甲船沿北偏西方向前进,乙船沿东北方向前进,
∴,,,
∴;
∵,
∴,
∵甲船沿北偏东的方向追赶乙船,
∴,
∴,
∴,
∴;
在中,,,
∴,
∴,
∵甲船以千米/小时的速度航行小时到达处,
∴(千米);
在中,,
∴(千米),
∴(千米),
∵,,
∴(千米),
且乙船以千米/小时的速度沿东北方向前进,
故甲船从处追赶上乙船的时间是:(小时).
(2)解:在中,,
∴(千米),
故甲船追赶乙船的速度是(千米/小时).
21.(1)如图2中,作于点O.
根据题意有:,
∵,
∴四边形是矩形,
∴,
∵,
∴,
∴(),
∴();
(2)作于F,于P,于G,于H.
则四边形是矩形,
∵根据(1)求出,,
∴,
∵,
∴,
∴(),(),
∴(),
∴下降高度:().
22.(1)∵,
∴,,
∴
∵四边形是平行四边形,
∴,,
∴,
∴,
∴,
∴四边形是平行四边形.
(2)∵在中,,
∴设,,
∵在中,,
即,
解得或(舍去)
∴,.
由(1)得:四边形是平行四边形,
∴,,
∵,
∴,
∴,
∴,
∴,
设,则,
∴,
解得:或(舍去),
即,
由(1)得,
∴,
∴.
23.(1)证明:∵四边形是矩形,
∴,
由折叠性质可得:,
∵延长交于E,
∴,
∴,
∵点M是的中点,
∴,
由折叠性质可得:,
∴,
∵,
∴,
∴,
∴平分;
(2)证明:由折叠性质可得:,
由(1)得:,
∵,
∴,
∵∠B=90°,
∵,
∴,
∵,
∴;
(3)解:由(2)得:,
∵,
∴,
由(2)得:,
由折叠性质得:,
∴,
∴,
∵,
∴,
∴,
由(1)得:,
∴,
∴,
由折叠性质的:,
∴,
∴,
∴;
24.(1)为直径,
,
又,,
.
,
,
.
(2)①连接.
,,,
,
,.
,
,
又,,
,
,,
.
②过点作,垂足为.
,,
,,
,,
.
由,得.
.
,
,
∵
∴.
由勾股定理得.
(3)解:如图所示,连接交于点,
,,
,
为直径,
.
为中点.
为的中位线,
,.
,
,
,
.
,
,
令,则,,
,,
.
