1.1认识三角形(1) 课件(共24张PPT)
文档属性
| 名称 | 1.1认识三角形(1) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
1.1认识三角形(1)
浙教版八年级上册
线段
角
相交线
平行线
三角形
一条线
两条线
三条线
射线
直线
B
A
●
●
A
B
●
●
●
●
B
A
温故知新
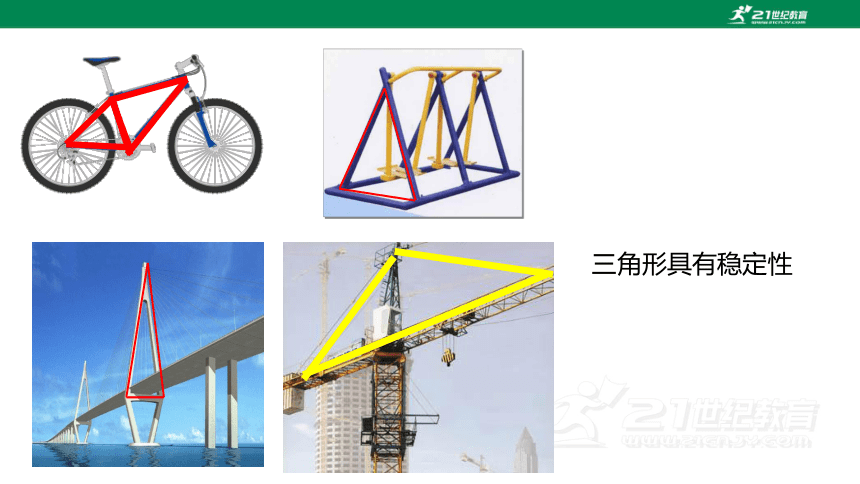
三角形具有稳定性
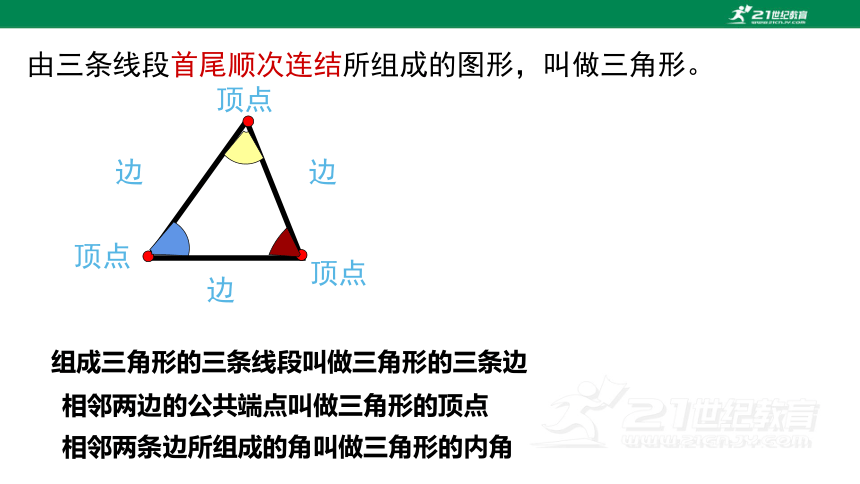
由三条线段首尾顺次连结所组成的图形,叫做三角形。
组成三角形的三条线段叫做三角形的三条边
相邻两边的公共端点叫做三角形的顶点
相邻两条边所组成的角叫做三角形的内角
边
边
边
顶点
顶点
顶点
3、三角形的三个内角:
2、三角形的三个顶点:
1、三角形的三条边:
c
b
a
B
C
A
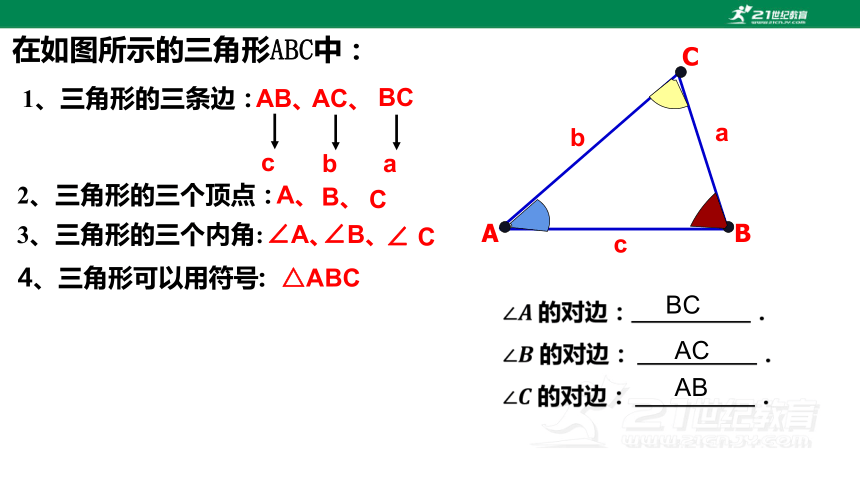
在如图所示的三角形ABC中:
a
b
c
4、三角形可以用符号:
△ABC
AB、
AC、
BC
∠A、
∠B、
∠ C
A、
C
B、
BC
AC
AB
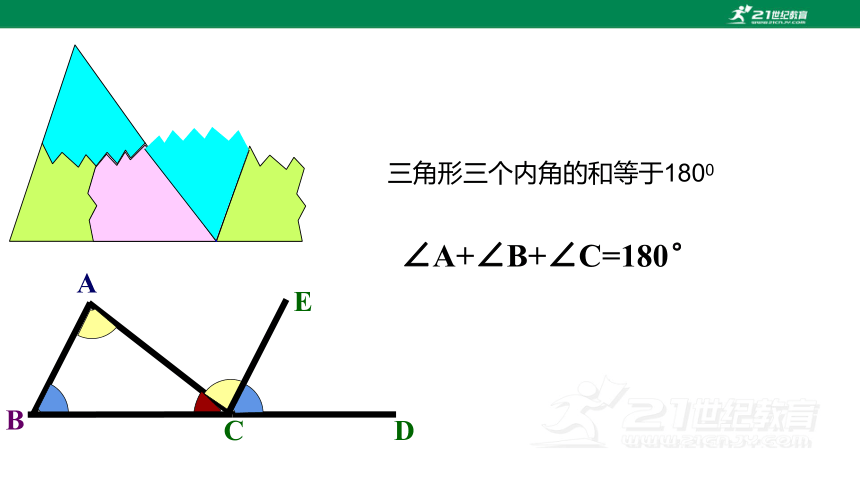
三角形三个内角的和等于1800
A
B
C
∠A+∠B+∠C=180°
D
E
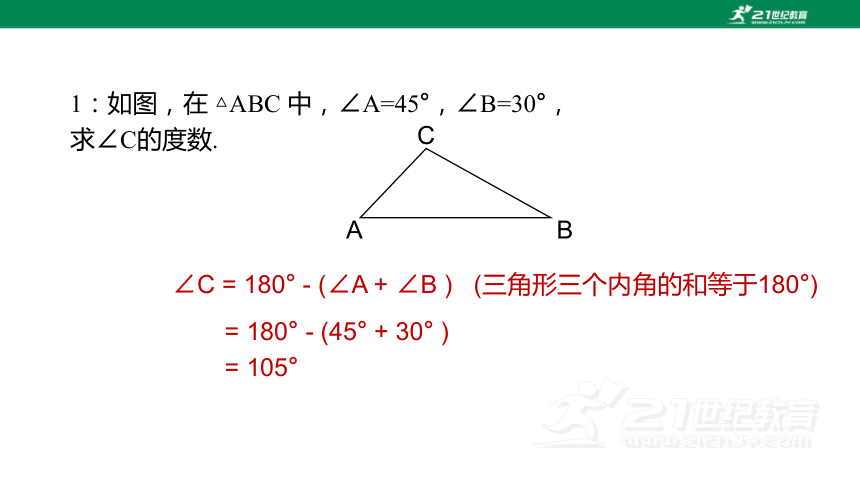
1:如图,在 △ABC 中,∠A=45°,∠B=30°,求∠C的度数.
C
A
B
∠C = 180° - (∠A + ∠B ) (三角形三个内角的和等于180°)
= 180° - (45° + 30° )
= 105°
变式1:在△ABC中,∠A=100°,∠B=∠C,求∠B的度数.
变式2:在△ABC中,∠A=∠B=∠C,求∠A的度数.
变式3:在△ABC中,∠A:∠B:∠C=2:3:5,求∠A 、∠B、∠C的度数.
变式4:在△ABC中,∠A+∠B =∠C,求∠C的度数.
∠B==40°
∠A=60°
∠A=36°
∠C==90°
∠B=54°
∠C=90°
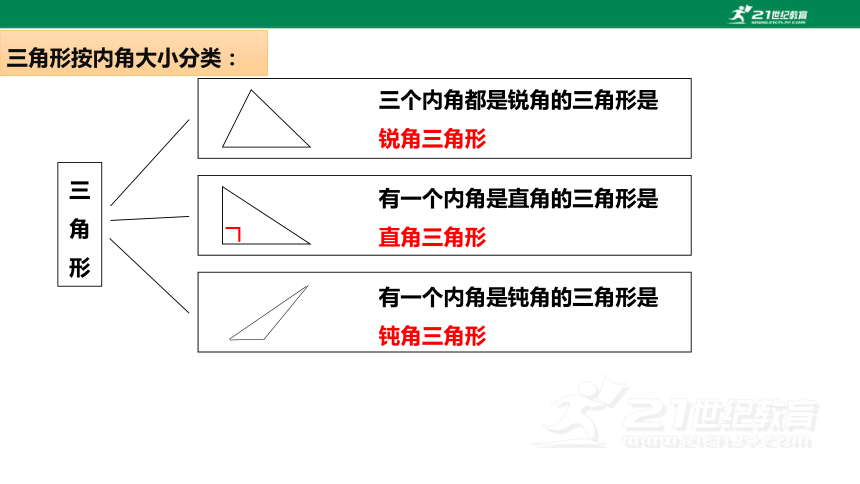
三角形按内角大小分类:
三
角
形
三个内角都是锐角的三角形是
锐角三角形
有一个内角是直角的三角形是
直角三角形
有一个内角是钝角的三角形是
钝角三角形
∟
2.一个三角形中:
最多有几个钝角?几个直角?几个锐角?
钝角三角形
直角三角形
锐角三角形
A
B
C
A
B
C
A
B
C
A
B
在A点的小狗,为了尽快吃到B点的骨头,它会选择哪条路线
C
性质:三角形任何两边的和大于第三边.
两点之间,线段最短
AC+BC>AB
AC+AB>BC
AB+BC>AC
如果小狗在C点呢?
3.长度为6cm, 4cm, 3cm三条线段能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
解: ∵最长线段是6cm
4+3>6
∴能组成三角形
只要满足较小的两条线段之和大于第三条线段,
便可构成三角形;若不满足,则不能构成三角形.
4.判断下列各组线段中,哪些能组成三角形,
哪些不能组成三角形,并说明理由
(1)a=2.5cm,b=3cm,c=5cm;
(2)e=6.3cm,f=6.3cm,g=12.6cm
解(1)∵ 最长线段是c=5cm,
a+b=2.5+3=5.5(cm)
∴ a+b>c.线段a,b,c能组成三角形。
(2)∵ 最长线段是g=12.6cm,
e+f=6.3+6.3=12.6(cm)
∴ e+f=g.线段e,f,g不能组成三角形。
A
B
C
AB+AC>BC. ①
由不等式②③移项可得
BC>AB-AC,BC>AC-AB.
AC+BC>AB, ②
AB+BC>AC. ③
三角形两边的差小于第三边.
三角形两边的和大于第三边.
两边之差<第三边<两边之和
a
c
b
b-cA
B
C
5.如图,在 △ABC 中,
AB =6,AC=4
1.求BC的取值范围?
4
6
2.若BC为偶数,则BC 的长为多少?
6-422BC为偶数
BC为4,6,8.
1: 已知△ABC中,∠A∶∠B∶∠C=1∶3∶5,求∠A、∠B和∠C的度数,它是什么三角形?
解:∵ ∠A∶∠B∶∠C=1∶3∶5,
且∠A+∠B+∠C=180°
设∠A=x 则∠B=3x ∠C=5x . 即x + 3x + 5x = 180°
∴ x =20° ∴ ∠A= 20° ,∠B= 60° ,∠C= 100°
△ABC为钝角三角形.
当堂练习:
40cm,50cm,60cm,
90cm,130cm
40cm
90cm
已有
商店
我该买哪种呢
?
C
90cm
40cm
x
A
B
50一个三角形有两边相等,已知其中一边是5cm,
另一边是9cm,则这个三角形的周长是______________
3、一个三角形有两边相等,已知其中一边是3cm,
另一边是9cm,则这个三角形的周长是______________
21cm
19cm或23cm
4.如图所示,P是△ABC内一点,连接PB、PC,比较PB+PC与AB+AC的大小?
A
P
B
C
PB+PC > BC
AB+AC > BC
{
不能判断
方法 ① 等量代换
方法 ② 拆分
Q
解:延长BP交AC于Q
AB+AC=AB+AQ+QC
>BQ+QC
=PB+PQ+QC
>PB+PC
AB+AQ > BQ PQ+QC > PC
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1认识三角形(1)
浙教版八年级上册
线段
角
相交线
平行线
三角形
一条线
两条线
三条线
射线
直线
B
A
●
●
A
B
●
●
●
●
B
A
温故知新
三角形具有稳定性
由三条线段首尾顺次连结所组成的图形,叫做三角形。
组成三角形的三条线段叫做三角形的三条边
相邻两边的公共端点叫做三角形的顶点
相邻两条边所组成的角叫做三角形的内角
边
边
边
顶点
顶点
顶点
3、三角形的三个内角:
2、三角形的三个顶点:
1、三角形的三条边:
c
b
a
B
C
A
在如图所示的三角形ABC中:
a
b
c
4、三角形可以用符号:
△ABC
AB、
AC、
BC
∠A、
∠B、
∠ C
A、
C
B、
BC
AC
AB
三角形三个内角的和等于1800
A
B
C
∠A+∠B+∠C=180°
D
E
1:如图,在 △ABC 中,∠A=45°,∠B=30°,求∠C的度数.
C
A
B
∠C = 180° - (∠A + ∠B ) (三角形三个内角的和等于180°)
= 180° - (45° + 30° )
= 105°
变式1:在△ABC中,∠A=100°,∠B=∠C,求∠B的度数.
变式2:在△ABC中,∠A=∠B=∠C,求∠A的度数.
变式3:在△ABC中,∠A:∠B:∠C=2:3:5,求∠A 、∠B、∠C的度数.
变式4:在△ABC中,∠A+∠B =∠C,求∠C的度数.
∠B==40°
∠A=60°
∠A=36°
∠C==90°
∠B=54°
∠C=90°
三角形按内角大小分类:
三
角
形
三个内角都是锐角的三角形是
锐角三角形
有一个内角是直角的三角形是
直角三角形
有一个内角是钝角的三角形是
钝角三角形
∟
2.一个三角形中:
最多有几个钝角?几个直角?几个锐角?
钝角三角形
直角三角形
锐角三角形
A
B
C
A
B
C
A
B
C
A
B
在A点的小狗,为了尽快吃到B点的骨头,它会选择哪条路线
C
性质:三角形任何两边的和大于第三边.
两点之间,线段最短
AC+BC>AB
AC+AB>BC
AB+BC>AC
如果小狗在C点呢?
3.长度为6cm, 4cm, 3cm三条线段能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
解: ∵最长线段是6cm
4+3>6
∴能组成三角形
只要满足较小的两条线段之和大于第三条线段,
便可构成三角形;若不满足,则不能构成三角形.
4.判断下列各组线段中,哪些能组成三角形,
哪些不能组成三角形,并说明理由
(1)a=2.5cm,b=3cm,c=5cm;
(2)e=6.3cm,f=6.3cm,g=12.6cm
解(1)∵ 最长线段是c=5cm,
a+b=2.5+3=5.5(cm)
∴ a+b>c.线段a,b,c能组成三角形。
(2)∵ 最长线段是g=12.6cm,
e+f=6.3+6.3=12.6(cm)
∴ e+f=g.线段e,f,g不能组成三角形。
A
B
C
AB+AC>BC. ①
由不等式②③移项可得
BC>AB-AC,BC>AC-AB.
AC+BC>AB, ②
AB+BC>AC. ③
三角形两边的差小于第三边.
三角形两边的和大于第三边.
两边之差<第三边<两边之和
a
c
b
b-c
B
C
5.如图,在 △ABC 中,
AB =6,AC=4
1.求BC的取值范围?
4
6
2.若BC为偶数,则BC 的长为多少?
6-4
BC为4,6,8.
1: 已知△ABC中,∠A∶∠B∶∠C=1∶3∶5,求∠A、∠B和∠C的度数,它是什么三角形?
解:∵ ∠A∶∠B∶∠C=1∶3∶5,
且∠A+∠B+∠C=180°
设∠A=x 则∠B=3x ∠C=5x . 即x + 3x + 5x = 180°
∴ x =20° ∴ ∠A= 20° ,∠B= 60° ,∠C= 100°
△ABC为钝角三角形.
当堂练习:
40cm,50cm,60cm,
90cm,130cm
40cm
90cm
已有
商店
我该买哪种呢
?
C
90cm
40cm
x
A
B
50
另一边是9cm,则这个三角形的周长是______________
3、一个三角形有两边相等,已知其中一边是3cm,
另一边是9cm,则这个三角形的周长是______________
21cm
19cm或23cm
4.如图所示,P是△ABC内一点,连接PB、PC,比较PB+PC与AB+AC的大小?
A
P
B
C
PB+PC > BC
AB+AC > BC
{
不能判断
方法 ① 等量代换
方法 ② 拆分
Q
解:延长BP交AC于Q
AB+AC=AB+AQ+QC
>BQ+QC
=PB+PQ+QC
>PB+PC
AB+AQ > BQ PQ+QC > PC
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
