1.1认识三角形(2) 课件(共18张PPT)
文档属性
| 名称 | 1.1认识三角形(2) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 18:51:53 | ||
图片预览


文档简介
(共18张PPT)
1.1认识三角形(2)
浙教版八年级上册
高是一条线段
顶点
顶点向对边所在直线引作垂线形成的垂足
关于三角形的高
{
A
B
C
D
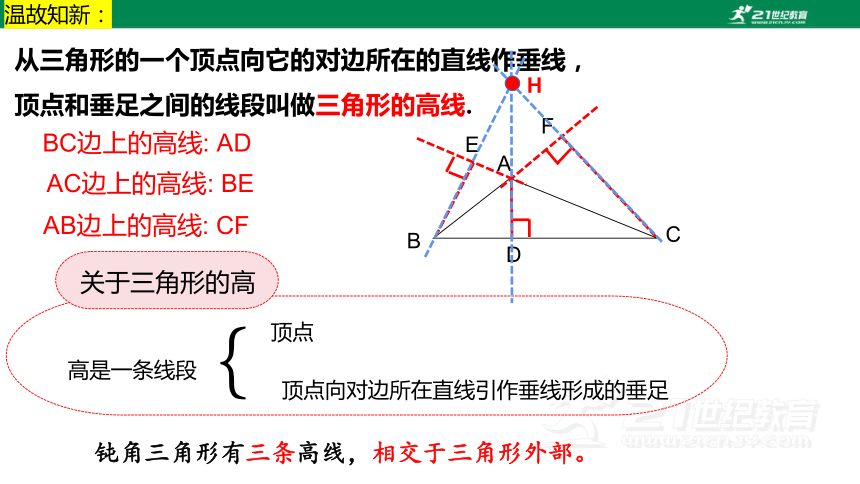
温故知新:
从三角形的一个顶点向它的对边所在的直线作垂线,
顶点和垂足之间的线段叫做三角形的高线.
BC边上的高线: AD
AC边上的高线: BE
E
AB边上的高线: CF
F
H
钝角三角形有三条高线,相交于三角形外部。
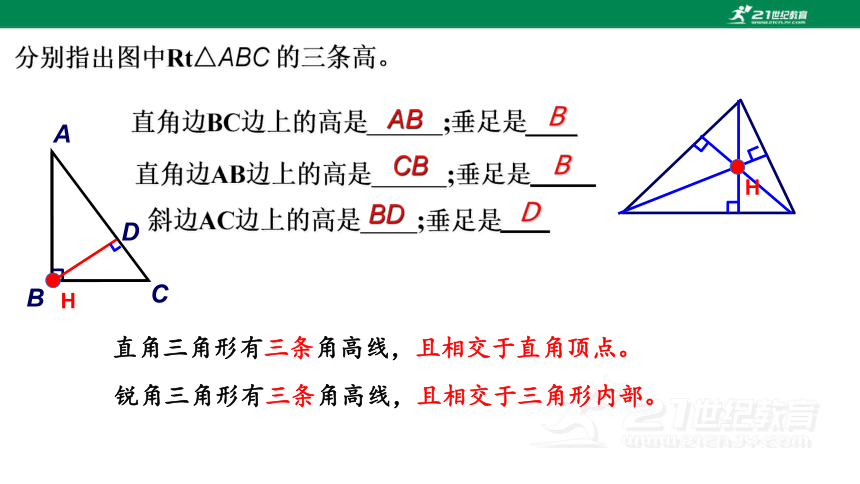
分别指出图中Rt△ABC 的三条高。
直角边BC边上的高是 ;垂足是____
AB
直角边AB边上的高是 ;垂足是____
CB
A
B
C
斜边AC边上的高是 ;垂足是___
BD
B
B
直角三角形有三条角高线,且相交于直角顶点。
D
H
H
D
锐角三角形有三条角高线,且相交于三角形内部。
A
B
C
D
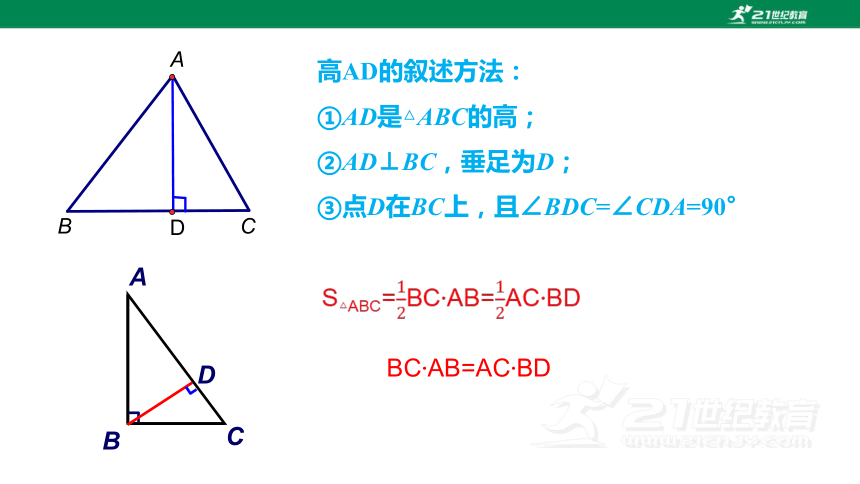
高AD的叙述方法:
①AD是△ABC的高;
②AD⊥BC,垂足为D;
③点D在BC上,且∠BDC=∠CDA=90°
A
B
C
D
BC AB=AC BD
S△ABC=BC AB=AC BD
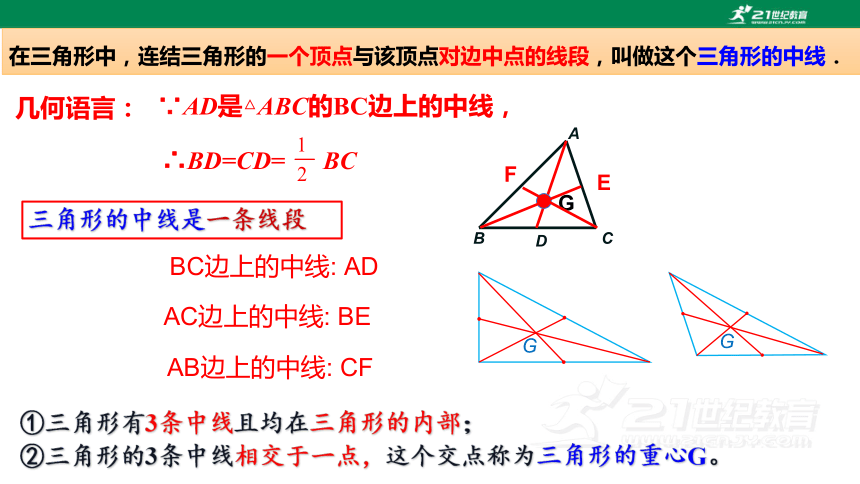
在三角形中,连结三角形的一个顶点与该顶点对边中点的线段,叫做这个三角形的中线.
A
D
C
B
∴BD=CD= BC
∵AD是△ABC的BC边上的中线,
三角形的中线是一条线段
几何语言:
①三角形有3条中线且均在三角形的内部;
②三角形的3条中线相交于一点,这个交点称为三角形的重心G。
BC边上的中线: AD
AC边上的中线: BE
AB边上的中线: CF
G
E
F
G
G
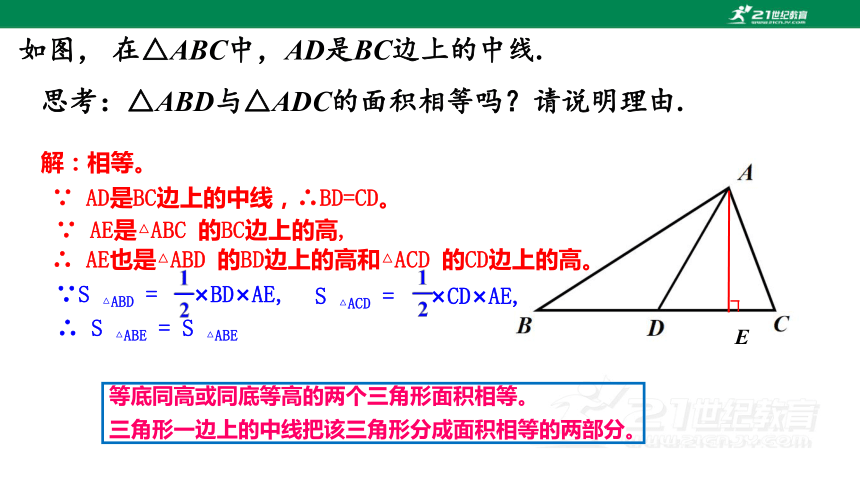
如图, 在△ABC中,AD是BC边上的中线.
思考:△ABD与△ADC的面积相等吗?请说明理由.
解:相等。
∵ AD是BC边上的中线,∴BD=CD。
∵ AE是△ABC 的BC边上的高,
∴ AE也是△ABD 的BD边上的高和△ACD 的CD边上的高。
∵S △ABD = ×BD×AE,
S △ACD = ×CD×AE,
∴ S △ABE = S △ABE
等底同高或同底等高的两个三角形面积相等。
三角形一边上的中线把该三角形分成面积相等的两部分。
E
如图,点D、E、F 分别是△ABC的三条边的中点.
设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AE. △AEC的面积是多少
(2)由第(1)题,你能求出△ECF的面积吗
△ADF和△DBE的面积呢
A
B
C
F
D
E
1.锐角三角形
O
2.直角三角形
O
3.钝角三角形
O
三角形的三条角平分线相交于一点,交点在三角形的内部.
A
B
D
C
三角形的角平分线:
∵AD是△ABC的一条角平分线,
∴∠BAD=∠DAC=∠BAC
在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段叫做三角形的角平分线.
如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O。
(1)当∠ABC=600,∠ACB=800时,求∠BOC的度数.
解: (1)∵ BD,CE分别是△ABC的角平分线,
∴∠OBC= ∠ABC
∴∠OBC= ∠ACB
∵∠ABC=600,∠ACB=800.
∴∠OBC= 600÷2= 300.
∴∠OCB= 800÷2= 400.
∵∠OBC+∠BOC+∠BOC=1800.
∴∠OBC= 1800-300-400 =1100
(2)当∠A=400时,求∠BOC的度数.
解: (2)∵ BD,CE分别是△ABC的角平分线,
∴∠OBC= ∠ABC
∠OBC= ∠ACB
∵∠ABC+∠ACB+∠A=1800. ∠A=400
∴∠ABC+∠ACB=1800-∠A=1800-400=1400.
∴∠OBC+∠OCB=
∠ABC+
∠ACB
(∠ABC+∠ACB)
= 1400÷2= 700.
(3)当∠A=x0时,求∠BOC的度数(用含 x的代数式表示).
解: (3)∵ BD,CE分别是△ABC的角平分线,
∴∠OBC= ∠ABC
∴∠OBC= ∠ACB
∵∠ABC+∠ACB+∠A=1800. ∠A=x0
∴∠ABC+∠ACB=1800-∠A=(180-x)0.
∴∠OBC+∠OCB=
∠ABC+
∠ACB
(∠ABC+∠ACB)
(180-x)0
=(90- x)0
1.下列图形中,△ ABC 的 AB 边上的高线画法正确的是( B )
A
B
B
C
D
当堂练习
2.在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.
已知∠BAC=80°,∠C=40°,求∠DAE的大小.
A
C
B
D
E
解: ∵ AE是△ABC的角平分线,且∠BAC=80°,
∴∠EAC=∠BAC=40°.
∵AD是△ABC的高线,∴∠ADC=90°,
∵∠DAC+∠ADC+∠C=180°,
∴∠DAC=180° - ∠ADC - ∠C=180° - 90° - 40°=50°,
∴∠DAE=∠DAC - ∠EAC=50° - 40°=10°.
3.已知△ABC中,AC=5cm。中线AD把△ABC分成两个小三角形, 这两个小三角形的周长的差是2cm。你能求出AB的长吗?
AB < AC
AB > AC
解: ∵ AD是△ABC的中线,∴BD=CD
∵C△ABD=AB+BD+AD,
C△ACD=AC+CD+AD,
∴C△ABD-C△ACD=|AB-AC|,
当AB>AC时,
AB-AC=2cm,
∵ AC=5cm,
当AC>AB时,
AC-AB=2cm,
同理得,
AB=5-2=3(cm)
∴AB=7cm,
4.如图AD是△ABC的中线,DE⊥AC,DF⊥AB,E、F分别是垂足,已知AB=2AC,求DE与DF的长度之比.
5.将这块三角形煎饼分成大小相同的6块。
如果限定只能切三刀呢?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1认识三角形(2)
浙教版八年级上册
高是一条线段
顶点
顶点向对边所在直线引作垂线形成的垂足
关于三角形的高
{
A
B
C
D
温故知新:
从三角形的一个顶点向它的对边所在的直线作垂线,
顶点和垂足之间的线段叫做三角形的高线.
BC边上的高线: AD
AC边上的高线: BE
E
AB边上的高线: CF
F
H
钝角三角形有三条高线,相交于三角形外部。
分别指出图中Rt△ABC 的三条高。
直角边BC边上的高是 ;垂足是____
AB
直角边AB边上的高是 ;垂足是____
CB
A
B
C
斜边AC边上的高是 ;垂足是___
BD
B
B
直角三角形有三条角高线,且相交于直角顶点。
D
H
H
D
锐角三角形有三条角高线,且相交于三角形内部。
A
B
C
D
高AD的叙述方法:
①AD是△ABC的高;
②AD⊥BC,垂足为D;
③点D在BC上,且∠BDC=∠CDA=90°
A
B
C
D
BC AB=AC BD
S△ABC=BC AB=AC BD
在三角形中,连结三角形的一个顶点与该顶点对边中点的线段,叫做这个三角形的中线.
A
D
C
B
∴BD=CD= BC
∵AD是△ABC的BC边上的中线,
三角形的中线是一条线段
几何语言:
①三角形有3条中线且均在三角形的内部;
②三角形的3条中线相交于一点,这个交点称为三角形的重心G。
BC边上的中线: AD
AC边上的中线: BE
AB边上的中线: CF
G
E
F
G
G
如图, 在△ABC中,AD是BC边上的中线.
思考:△ABD与△ADC的面积相等吗?请说明理由.
解:相等。
∵ AD是BC边上的中线,∴BD=CD。
∵ AE是△ABC 的BC边上的高,
∴ AE也是△ABD 的BD边上的高和△ACD 的CD边上的高。
∵S △ABD = ×BD×AE,
S △ACD = ×CD×AE,
∴ S △ABE = S △ABE
等底同高或同底等高的两个三角形面积相等。
三角形一边上的中线把该三角形分成面积相等的两部分。
E
如图,点D、E、F 分别是△ABC的三条边的中点.
设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AE. △AEC的面积是多少
(2)由第(1)题,你能求出△ECF的面积吗
△ADF和△DBE的面积呢
A
B
C
F
D
E
1.锐角三角形
O
2.直角三角形
O
3.钝角三角形
O
三角形的三条角平分线相交于一点,交点在三角形的内部.
A
B
D
C
三角形的角平分线:
∵AD是△ABC的一条角平分线,
∴∠BAD=∠DAC=∠BAC
在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段叫做三角形的角平分线.
如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O。
(1)当∠ABC=600,∠ACB=800时,求∠BOC的度数.
解: (1)∵ BD,CE分别是△ABC的角平分线,
∴∠OBC= ∠ABC
∴∠OBC= ∠ACB
∵∠ABC=600,∠ACB=800.
∴∠OBC= 600÷2= 300.
∴∠OCB= 800÷2= 400.
∵∠OBC+∠BOC+∠BOC=1800.
∴∠OBC= 1800-300-400 =1100
(2)当∠A=400时,求∠BOC的度数.
解: (2)∵ BD,CE分别是△ABC的角平分线,
∴∠OBC= ∠ABC
∠OBC= ∠ACB
∵∠ABC+∠ACB+∠A=1800. ∠A=400
∴∠ABC+∠ACB=1800-∠A=1800-400=1400.
∴∠OBC+∠OCB=
∠ABC+
∠ACB
(∠ABC+∠ACB)
= 1400÷2= 700.
(3)当∠A=x0时,求∠BOC的度数(用含 x的代数式表示).
解: (3)∵ BD,CE分别是△ABC的角平分线,
∴∠OBC= ∠ABC
∴∠OBC= ∠ACB
∵∠ABC+∠ACB+∠A=1800. ∠A=x0
∴∠ABC+∠ACB=1800-∠A=(180-x)0.
∴∠OBC+∠OCB=
∠ABC+
∠ACB
(∠ABC+∠ACB)
(180-x)0
=(90- x)0
1.下列图形中,△ ABC 的 AB 边上的高线画法正确的是( B )
A
B
B
C
D
当堂练习
2.在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.
已知∠BAC=80°,∠C=40°,求∠DAE的大小.
A
C
B
D
E
解: ∵ AE是△ABC的角平分线,且∠BAC=80°,
∴∠EAC=∠BAC=40°.
∵AD是△ABC的高线,∴∠ADC=90°,
∵∠DAC+∠ADC+∠C=180°,
∴∠DAC=180° - ∠ADC - ∠C=180° - 90° - 40°=50°,
∴∠DAE=∠DAC - ∠EAC=50° - 40°=10°.
3.已知△ABC中,AC=5cm。中线AD把△ABC分成两个小三角形, 这两个小三角形的周长的差是2cm。你能求出AB的长吗?
AB < AC
AB > AC
解: ∵ AD是△ABC的中线,∴BD=CD
∵C△ABD=AB+BD+AD,
C△ACD=AC+CD+AD,
∴C△ABD-C△ACD=|AB-AC|,
当AB>AC时,
AB-AC=2cm,
∵ AC=5cm,
当AC>AB时,
AC-AB=2cm,
同理得,
AB=5-2=3(cm)
∴AB=7cm,
4.如图AD是△ABC的中线,DE⊥AC,DF⊥AB,E、F分别是垂足,已知AB=2AC,求DE与DF的长度之比.
5.将这块三角形煎饼分成大小相同的6块。
如果限定只能切三刀呢?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
