1.2 定义与命题(1) 课件(共20张PPT)
文档属性
| 名称 | 1.2 定义与命题(1) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 18:52:42 | ||
图片预览





文档简介
(共20张PPT)
1.2定义与命题(1)
浙教版八年级上册
一般地,能清楚地规定某一名称或术语的意义的句子
叫做该名称或术语的定义.
在同一平面内,不相交的两条直线叫做
商店降低商品的定价出售商品叫做
打折;
平行线。
说出下列数学名词的定义:
(1) 叫做无理数。
(2) 称为抽样调查。
无限不循环小数
齐声朗读:
从所有对象中抽取一部分作调查分析,
“鸟是动物.”
对一件事情没有作出判断。
对一件事情作出了判断
“鸟是动物吗 ”
一般地,判断某一件事情的句子叫做命题.
下列句子,哪些对事情作了判断,哪些没有对事情作出判断?
⑴对顶角相等; ⑵画一个角等于已知角;
⑶两直线平行,同位角相等; ⑷a、b两条直线平行吗?
(5)若a2= b2,则a=b; ⑹若a2=4,求a的值;
句子_____________ 对事情作了判断;
句子 没有对事情作出判断.
(1)
(3)
(5)
(2)
(4)
(6)
命题
不是命题
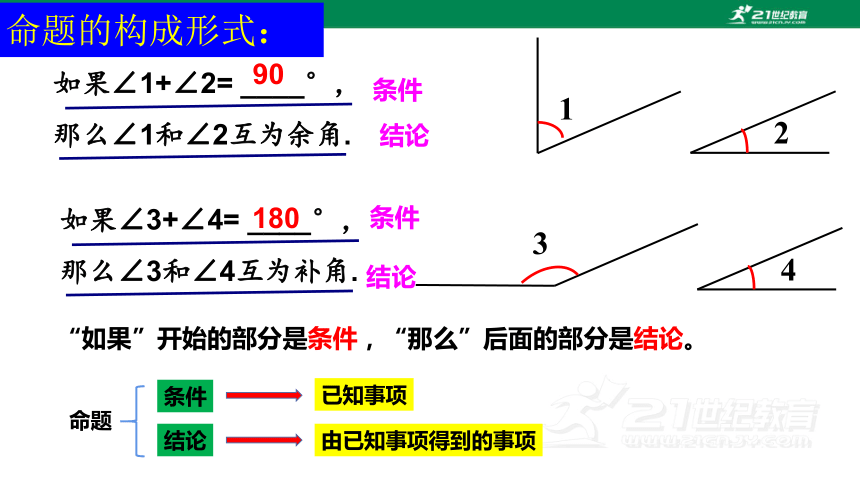
如果∠1+∠2= ____°,
那么∠1和∠2互为余角.
90
1
2
条件
结论
如果∠3+∠4= ____°,
那么∠3和∠4互为补角.
3
4
条件
结论
180
命题
条件
结论
已知事项
由已知事项得到的事项
“如果”开始的部分是条件,“那么”后面的部分是结论。
命题的构成形式:
命题 条件 结论
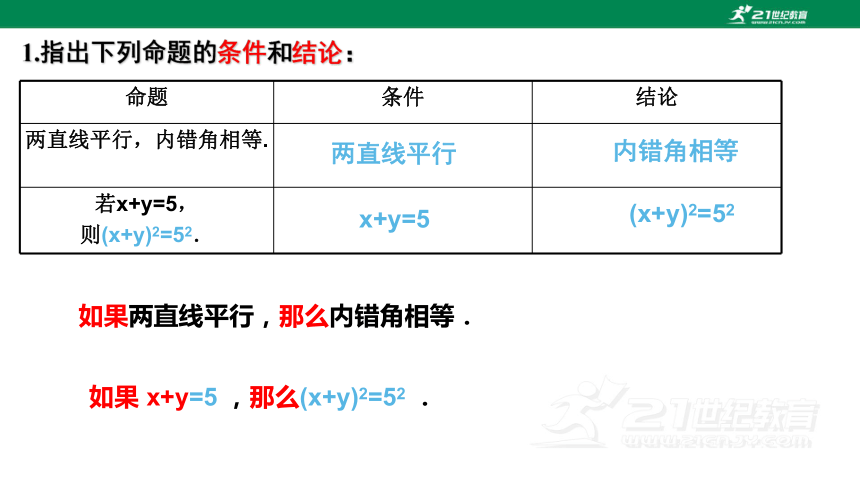
两直线平行,内错角相等.
若x+y=5, 则(x+y)2=52.
1.指出下列命题的条件和结论:
两直线平行
内错角相等
(x+y)2=52
如果两直线平行,那么内错角相等.
如果 x+y=5 ,那么(x+y)2=52 .
x+y=5
2.指出下列命题的条件和结论,并改写“如果……那 么……”的形式:
(1) 绝对值相等的两个数相等或互为相反数;
(2)直角三角形两个锐角互余。
(3)在直角三角形中,斜边大于直角边。
如果两个数的绝对值相等,那么这两个数相等或互为相反数。
如果两个角是一个直角三角形的两个锐角,那么这两个角互余。
如果一个三角形是直角三角形,那么它的斜边大于直角边。
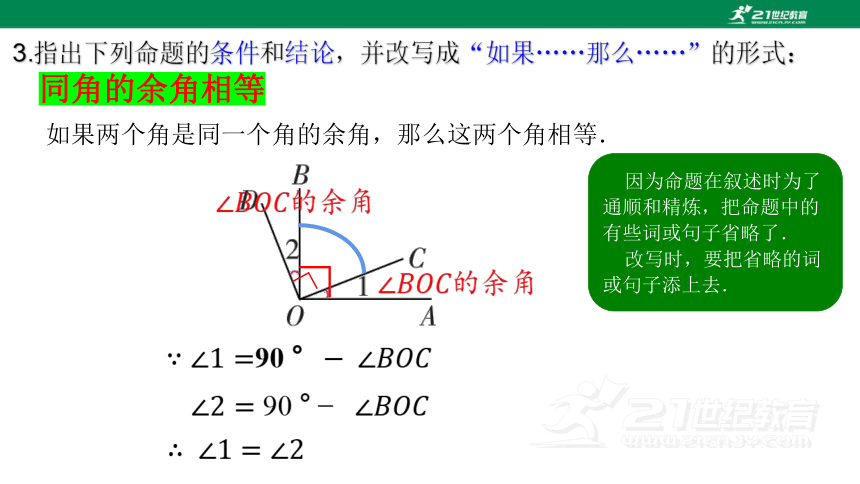
同角的余角相等
3.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
如果两个角是同一个角的余角,那么这两个角相等.
∟
∟
因为命题在叙述时为了
通顺和精炼,把命题中的
有些词或句子省略了.
改写时,要把省略的词
或句子添上去.
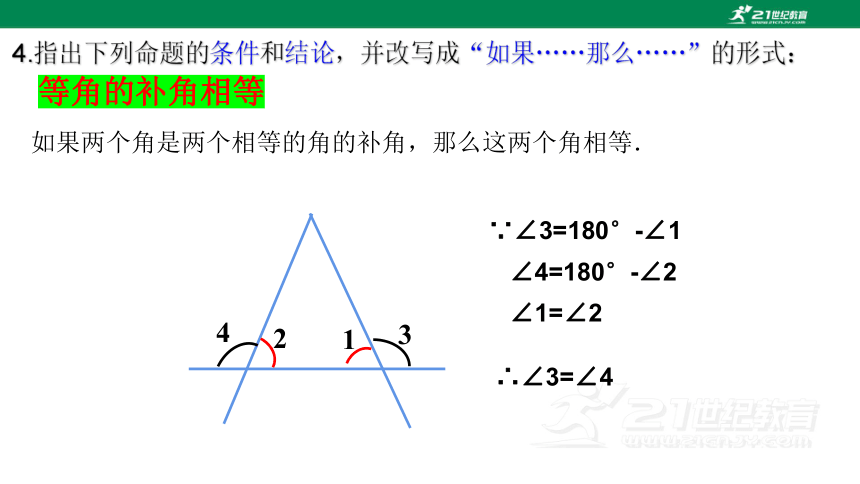
等角的补角相等
4.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
如果两个角是两个相等的角的补角,那么这两个角相等.
2
3
1
4
∵∠3=180°-∠1
∠4=180°-∠2
∠1=∠2
∴∠3=∠4
等角的余角相等
指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
如果两个角是两个相等的角的余角,那么这两个角相等.
2
3
1
4
∵∠3=90°-∠1
∠4=90°-∠2
∠1=∠2
∴∠3=∠4
5. 指出下列命题的条件和结论,并改写成
“如果……那么……”的形式:
(1) 等底等高的两个三角形面积相等;
如果两个三角形有一条边和这条边上的高线对应相等,
那么这两个三角形的面积相等。
条件是:
结论是:
改写成:
两个三角形有一条边和这条边上的高线对应相等
这两个三角形的面积相等
如果两个角是对顶角,那么这两个角相等。
两个角是对顶角
这两个角相等
(2) 对顶角相等;
条件是:
结论是:
改写成:
如果两条直线被第三条直线所截的同位角相等,
那么这两条直线平行。
两条直线被第三条直线所截的同位角相等
这两条直线平行
(3) 同位角相等,两直线平行;
条件是:
结论是:
改写成:
定义:
一般地,能清楚地规定某一名称或术语的意义 的句子叫做该名称或术语的定义。
命题:
对某一件事情作出判断的句子叫做命题.
命题可看做由条件和结论两部分组成.
条件是已知事项,结论是由已知事项推出的事项.
知识小结
命题是一个陈述句,就是判断一件事情的句子.
而定义是对事物的本质特征属性进行描述,也是命题
1. 下列句子中,哪些是命题?哪些不是命题?
(1)正数大于一切负数吗?
(2)两点之间线段最短。
(3) 不是无理数。
(4)作一条直线和已知直线平行。
(√)
(√)
(×)
(×)
当堂检测:
---是否作出判断
----与判断是否正确无关.
(5)2+3≠5.
(√)
对某一件事情作出正确或不正确的判断的句子叫做命题.
2.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是( )
A.如果同角,那么相等
B.如果同角,那么余角相等
C.如果同角的余角,那么相等
D.如果有两个角是同一个角的余角,那么这两个角相等
D
3.把下列命题写成“如果……那么……”的形式.
(1)三角形的内角和等于180°.
如果过直线外一点作已知直线的平行线,那么这样的直线有且只有一条.
如果三个角是三角形的三个内角,那么它们的和为180°.
(2)过直线外一点有且只有一条直线与已知直线平行.
4.若一个正整数能表示为两个连续偶数的平方差,那么这个正整数为“神秘数”.如4=22-02,12=42-22,20=62-42,
因此4,12,20这三个数都是神秘数.
(1)28和76是神秘数吗?为什么?
解:是.∵28=82-62,76=202-182,
∴28和76是神秘数.
(2)设两个连续偶数为2k+2和2k(k为非负整数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?
解:是.∵(2k+2)2-(2k)2=8k+4=4(2k+1),
∴由这两个连续偶数构成的神秘数是4的倍数.
5.观察下面四组图形,找出每一组图形的共同特征,并对类似于这样的图形下一个定义.
⑴
⑵
⑶
⑷
如:一个图形由另一个图形改变而来,在改变的过程中保持形状不变(大小可以改变)这个图形和原图形叫做相似图形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2定义与命题(1)
浙教版八年级上册
一般地,能清楚地规定某一名称或术语的意义的句子
叫做该名称或术语的定义.
在同一平面内,不相交的两条直线叫做
商店降低商品的定价出售商品叫做
打折;
平行线。
说出下列数学名词的定义:
(1) 叫做无理数。
(2) 称为抽样调查。
无限不循环小数
齐声朗读:
从所有对象中抽取一部分作调查分析,
“鸟是动物.”
对一件事情没有作出判断。
对一件事情作出了判断
“鸟是动物吗 ”
一般地,判断某一件事情的句子叫做命题.
下列句子,哪些对事情作了判断,哪些没有对事情作出判断?
⑴对顶角相等; ⑵画一个角等于已知角;
⑶两直线平行,同位角相等; ⑷a、b两条直线平行吗?
(5)若a2= b2,则a=b; ⑹若a2=4,求a的值;
句子_____________ 对事情作了判断;
句子 没有对事情作出判断.
(1)
(3)
(5)
(2)
(4)
(6)
命题
不是命题
如果∠1+∠2= ____°,
那么∠1和∠2互为余角.
90
1
2
条件
结论
如果∠3+∠4= ____°,
那么∠3和∠4互为补角.
3
4
条件
结论
180
命题
条件
结论
已知事项
由已知事项得到的事项
“如果”开始的部分是条件,“那么”后面的部分是结论。
命题的构成形式:
命题 条件 结论
两直线平行,内错角相等.
若x+y=5, 则(x+y)2=52.
1.指出下列命题的条件和结论:
两直线平行
内错角相等
(x+y)2=52
如果两直线平行,那么内错角相等.
如果 x+y=5 ,那么(x+y)2=52 .
x+y=5
2.指出下列命题的条件和结论,并改写“如果……那 么……”的形式:
(1) 绝对值相等的两个数相等或互为相反数;
(2)直角三角形两个锐角互余。
(3)在直角三角形中,斜边大于直角边。
如果两个数的绝对值相等,那么这两个数相等或互为相反数。
如果两个角是一个直角三角形的两个锐角,那么这两个角互余。
如果一个三角形是直角三角形,那么它的斜边大于直角边。
同角的余角相等
3.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
如果两个角是同一个角的余角,那么这两个角相等.
∟
∟
因为命题在叙述时为了
通顺和精炼,把命题中的
有些词或句子省略了.
改写时,要把省略的词
或句子添上去.
等角的补角相等
4.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
如果两个角是两个相等的角的补角,那么这两个角相等.
2
3
1
4
∵∠3=180°-∠1
∠4=180°-∠2
∠1=∠2
∴∠3=∠4
等角的余角相等
指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
如果两个角是两个相等的角的余角,那么这两个角相等.
2
3
1
4
∵∠3=90°-∠1
∠4=90°-∠2
∠1=∠2
∴∠3=∠4
5. 指出下列命题的条件和结论,并改写成
“如果……那么……”的形式:
(1) 等底等高的两个三角形面积相等;
如果两个三角形有一条边和这条边上的高线对应相等,
那么这两个三角形的面积相等。
条件是:
结论是:
改写成:
两个三角形有一条边和这条边上的高线对应相等
这两个三角形的面积相等
如果两个角是对顶角,那么这两个角相等。
两个角是对顶角
这两个角相等
(2) 对顶角相等;
条件是:
结论是:
改写成:
如果两条直线被第三条直线所截的同位角相等,
那么这两条直线平行。
两条直线被第三条直线所截的同位角相等
这两条直线平行
(3) 同位角相等,两直线平行;
条件是:
结论是:
改写成:
定义:
一般地,能清楚地规定某一名称或术语的意义 的句子叫做该名称或术语的定义。
命题:
对某一件事情作出判断的句子叫做命题.
命题可看做由条件和结论两部分组成.
条件是已知事项,结论是由已知事项推出的事项.
知识小结
命题是一个陈述句,就是判断一件事情的句子.
而定义是对事物的本质特征属性进行描述,也是命题
1. 下列句子中,哪些是命题?哪些不是命题?
(1)正数大于一切负数吗?
(2)两点之间线段最短。
(3) 不是无理数。
(4)作一条直线和已知直线平行。
(√)
(√)
(×)
(×)
当堂检测:
---是否作出判断
----与判断是否正确无关.
(5)2+3≠5.
(√)
对某一件事情作出正确或不正确的判断的句子叫做命题.
2.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是( )
A.如果同角,那么相等
B.如果同角,那么余角相等
C.如果同角的余角,那么相等
D.如果有两个角是同一个角的余角,那么这两个角相等
D
3.把下列命题写成“如果……那么……”的形式.
(1)三角形的内角和等于180°.
如果过直线外一点作已知直线的平行线,那么这样的直线有且只有一条.
如果三个角是三角形的三个内角,那么它们的和为180°.
(2)过直线外一点有且只有一条直线与已知直线平行.
4.若一个正整数能表示为两个连续偶数的平方差,那么这个正整数为“神秘数”.如4=22-02,12=42-22,20=62-42,
因此4,12,20这三个数都是神秘数.
(1)28和76是神秘数吗?为什么?
解:是.∵28=82-62,76=202-182,
∴28和76是神秘数.
(2)设两个连续偶数为2k+2和2k(k为非负整数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?
解:是.∵(2k+2)2-(2k)2=8k+4=4(2k+1),
∴由这两个连续偶数构成的神秘数是4的倍数.
5.观察下面四组图形,找出每一组图形的共同特征,并对类似于这样的图形下一个定义.
⑴
⑵
⑶
⑷
如:一个图形由另一个图形改变而来,在改变的过程中保持形状不变(大小可以改变)这个图形和原图形叫做相似图形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
