1.3 证明(1) 课件(共20张PPT)
文档属性
| 名称 | 1.3 证明(1) 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 18:55:11 | ||
图片预览






文档简介
(共20张PPT)
1.3 证明(1)
浙教版八年级上册
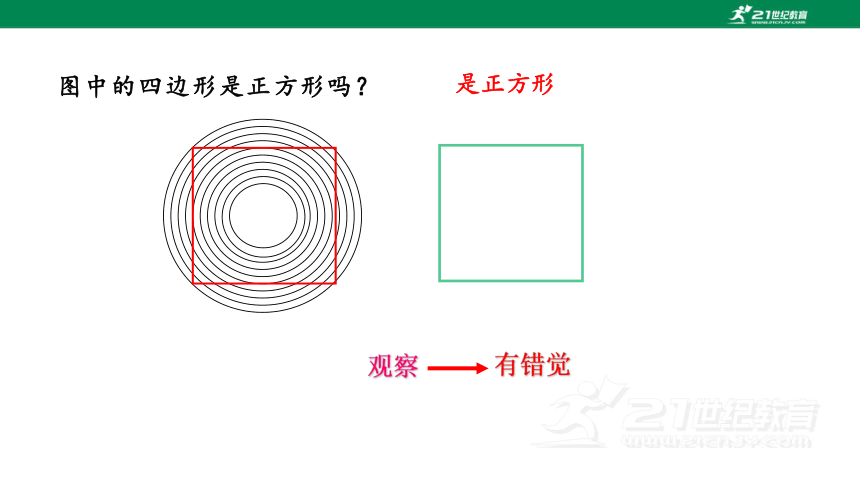
图中的四边形是正方形吗?
是正方形
观察
有错觉
直线a,b,c,d互相平行
图中的直线a,b,c,d是否都互相平行?
类似的猜想
当n=0时
当n=1时,
当n=2时,
当n=3时,
当n=4时,
=_____。
7
5
5
7
=_____。
=_____。
=_____。
=_____。
11
=_____。
当n=6时,
25
命题:对于自然数n,代数式n -3n+7的值都是质数
列 举
不胜举!
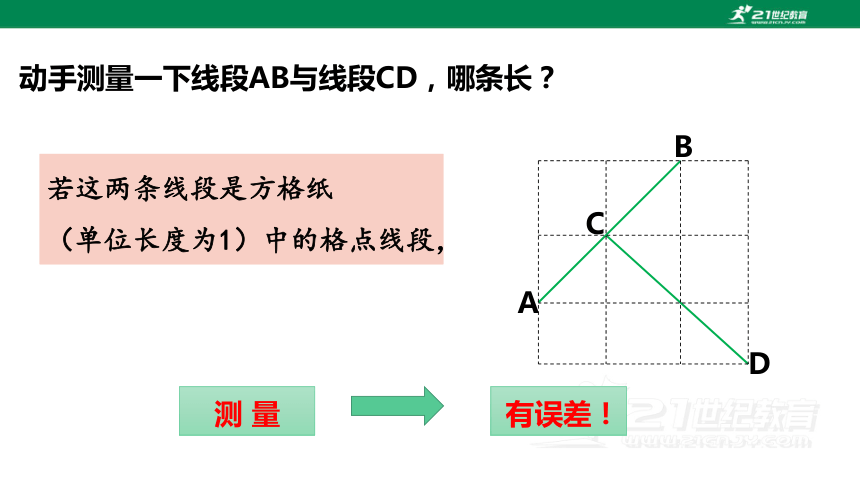
动手测量一下线段AB与线段CD,哪条长?
若这两条线段是方格纸
(单位长度为1)中的格点线段,
B
A
C
D
测 量
有误差!
要判断一个命题是真命题,往往需要从命题的条件
出发,根据已知的定义、基本事实、定理推论,
一步一步推得结论成立.这样的推理过程叫做证明.
观察
有错觉
测量
有误差
列举
不胜举
1. 证明命题:直角三角形的两个锐角互余.
已知:如图,在△ABC中,∠C=90°.
求证:∠A+∠B=90°.
证明:∵∠A+∠B+∠C=180°(三角形的内角和等于180°),
又∵∠C=90°(已知),
∴∠A+∠B=180°-∠C=90°(等式的性质).
分析:要证明OE⊥OF,只要证明
∠EOF= 90°,即∠1+∠2= 90°即可.
2.证明:邻补角的平分线互相垂直.
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
证明:∵OE平分∠AOB, ∴∠1= ∠AOB.
∵OF平分 ∠BOC, ∴∠2= ∠BOC.
∴∠1+∠2= (∠AOB+∠BOC) = ∠AOC = ×180°=90°.
∴OE⊥OF(垂直定义).
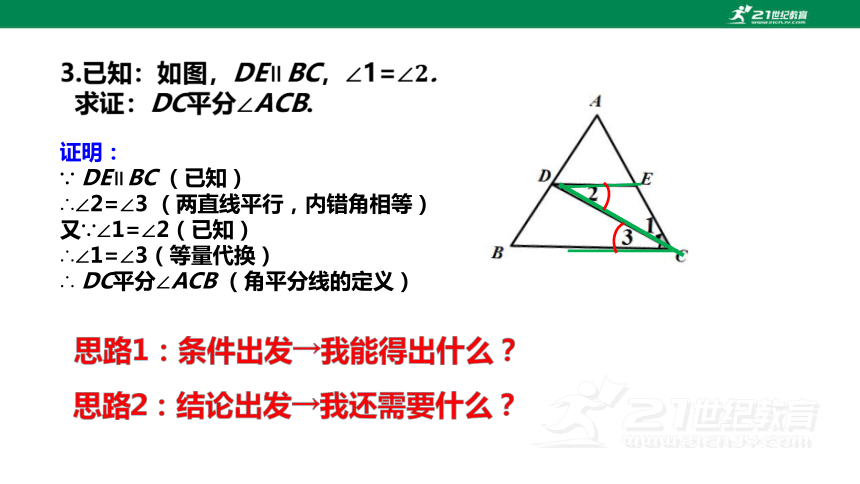
证明:
∵ DE∥BC (已知)
∴∠2=∠3 (两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴ DC平分∠ACB (角平分线的定义)
4. 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE.
求证:∠PEF+∠PFE=90°.
A
B
C
D
E
P
F
课堂小结
(1)证明过程
(2)证明思路
基于条件
依据已学
步步递推
证实判断
思路1:条件出发
思路2:结论出发
得出什么?
还需什么?
1. 已知:如图,在△ABC中,D,E分别为AB,AC上的点,且∠1=∠2.
求证:∠B=∠ADE.
证明:
∵ ∠1=∠2 ( )
∴ ∥ (内错角相等,两直线平行)
∴ ∠B=∠ADE ( )
已知
DE
BC
两直线平行,同位角相等
当堂检测:
2.已知:如图,∠ACD=2∠B,CE平分∠ACD. 求证:CE//AB.
证明:
∵CE平分∠ACD(已知),
∵ ∠ACD=2∠B(已知),
∴ 2∠B= 2∠DCE,(等量代换)
∴ CE//AB(同位角相等,两直线平行).
∴ ∠ ACD= 2∠DCE (角平分线的定义).
∴ ∠B=∠DCE,
3.填空(将下面的推理过程及依据补充完整).如图,点E在DF上,点B在AC上,已知∠1=∠2,∠3=∠4,求证:∠A=∠F.
证明:∵∠1=∠2(已知),∠2=∠DGF( ),
∴∠1=∠DGF,
∴BD∥CE( ),
∴∠3+∠C=180°( ).
又∵∠3=∠4(已知),∴∠4+∠C=180°,
∴DF∥AC( ),
∴∠A=∠F(两直线平行,内错角相等).
对顶角相等
同位角相等,两直线平行
两直线平行,同旁内角互补
同旁内角互补,两直线平行
4.证明命题:”一个角的两边分别平行于另一个角的两边,
且方向相同,则这两个角相等”是真命题.
已知:如图AB∥DE,BC∥EF.
求证:∠B=∠E
证明:∵AB∥DE (已知)
∴ ∠B= ∠DGC (两直线平行, 同位角相等)
∵BC∥EF (已知)
∴∠DGC =∠ E (两直线平行, 同位角相等)
∴ ∠B =∠ E. (等量代换)
A
B
C
D
E
F
G
思考:若把方向相同去掉会怎么样?
A
B
C
D
E
F
G
D
E
F
A
B
C
G
A
B
C
D
E
F
G
A
B
C
D
E
F
A
B
C
D
E
F
G
证明:一个角的两边分别平行于另一个角的两边,则这两个角相等或互补
5. 已知:如图,在△ABC中,∠B=∠C, D,E分别为AB,AC上的点,
且∠ADE=∠AED.
求证:DE//BC
A
B
C
D
E
∴ ∠B=∠ADE
∴ DE//BC
6.如图,BC⊥ AC于点C,CD⊥AB于点D,∠EBC=∠A,
求证:BE∥CD.
E
B
A
C
D
证明: ∵BC⊥AC(已知)
∴∠BCA=90° (垂直的定义)
∴∠BCD+∠ACD=90°
∵CD⊥AB (已知)
∴∠A+∠ACD=90°(直角三角形中两个锐角互余)
∴∠BCD=∠A (同角的余角相等)
又∵∠EBC=∠A(已知)
∴∠EBC=∠BCD
∴BE∥CD( 内错角相等,两直线平行)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3 证明(1)
浙教版八年级上册
图中的四边形是正方形吗?
是正方形
观察
有错觉
直线a,b,c,d互相平行
图中的直线a,b,c,d是否都互相平行?
类似的猜想
当n=0时
当n=1时,
当n=2时,
当n=3时,
当n=4时,
=_____。
7
5
5
7
=_____。
=_____。
=_____。
=_____。
11
=_____。
当n=6时,
25
命题:对于自然数n,代数式n -3n+7的值都是质数
列 举
不胜举!
动手测量一下线段AB与线段CD,哪条长?
若这两条线段是方格纸
(单位长度为1)中的格点线段,
B
A
C
D
测 量
有误差!
要判断一个命题是真命题,往往需要从命题的条件
出发,根据已知的定义、基本事实、定理推论,
一步一步推得结论成立.这样的推理过程叫做证明.
观察
有错觉
测量
有误差
列举
不胜举
1. 证明命题:直角三角形的两个锐角互余.
已知:如图,在△ABC中,∠C=90°.
求证:∠A+∠B=90°.
证明:∵∠A+∠B+∠C=180°(三角形的内角和等于180°),
又∵∠C=90°(已知),
∴∠A+∠B=180°-∠C=90°(等式的性质).
分析:要证明OE⊥OF,只要证明
∠EOF= 90°,即∠1+∠2= 90°即可.
2.证明:邻补角的平分线互相垂直.
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
证明:∵OE平分∠AOB, ∴∠1= ∠AOB.
∵OF平分 ∠BOC, ∴∠2= ∠BOC.
∴∠1+∠2= (∠AOB+∠BOC) = ∠AOC = ×180°=90°.
∴OE⊥OF(垂直定义).
证明:
∵ DE∥BC (已知)
∴∠2=∠3 (两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴ DC平分∠ACB (角平分线的定义)
4. 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE.
求证:∠PEF+∠PFE=90°.
A
B
C
D
E
P
F
课堂小结
(1)证明过程
(2)证明思路
基于条件
依据已学
步步递推
证实判断
思路1:条件出发
思路2:结论出发
得出什么?
还需什么?
1. 已知:如图,在△ABC中,D,E分别为AB,AC上的点,且∠1=∠2.
求证:∠B=∠ADE.
证明:
∵ ∠1=∠2 ( )
∴ ∥ (内错角相等,两直线平行)
∴ ∠B=∠ADE ( )
已知
DE
BC
两直线平行,同位角相等
当堂检测:
2.已知:如图,∠ACD=2∠B,CE平分∠ACD. 求证:CE//AB.
证明:
∵CE平分∠ACD(已知),
∵ ∠ACD=2∠B(已知),
∴ 2∠B= 2∠DCE,(等量代换)
∴ CE//AB(同位角相等,两直线平行).
∴ ∠ ACD= 2∠DCE (角平分线的定义).
∴ ∠B=∠DCE,
3.填空(将下面的推理过程及依据补充完整).如图,点E在DF上,点B在AC上,已知∠1=∠2,∠3=∠4,求证:∠A=∠F.
证明:∵∠1=∠2(已知),∠2=∠DGF( ),
∴∠1=∠DGF,
∴BD∥CE( ),
∴∠3+∠C=180°( ).
又∵∠3=∠4(已知),∴∠4+∠C=180°,
∴DF∥AC( ),
∴∠A=∠F(两直线平行,内错角相等).
对顶角相等
同位角相等,两直线平行
两直线平行,同旁内角互补
同旁内角互补,两直线平行
4.证明命题:”一个角的两边分别平行于另一个角的两边,
且方向相同,则这两个角相等”是真命题.
已知:如图AB∥DE,BC∥EF.
求证:∠B=∠E
证明:∵AB∥DE (已知)
∴ ∠B= ∠DGC (两直线平行, 同位角相等)
∵BC∥EF (已知)
∴∠DGC =∠ E (两直线平行, 同位角相等)
∴ ∠B =∠ E. (等量代换)
A
B
C
D
E
F
G
思考:若把方向相同去掉会怎么样?
A
B
C
D
E
F
G
D
E
F
A
B
C
G
A
B
C
D
E
F
G
A
B
C
D
E
F
A
B
C
D
E
F
G
证明:一个角的两边分别平行于另一个角的两边,则这两个角相等或互补
5. 已知:如图,在△ABC中,∠B=∠C, D,E分别为AB,AC上的点,
且∠ADE=∠AED.
求证:DE//BC
A
B
C
D
E
∴ ∠B=∠ADE
∴ DE//BC
6.如图,BC⊥ AC于点C,CD⊥AB于点D,∠EBC=∠A,
求证:BE∥CD.
E
B
A
C
D
证明: ∵BC⊥AC(已知)
∴∠BCA=90° (垂直的定义)
∴∠BCD+∠ACD=90°
∵CD⊥AB (已知)
∴∠A+∠ACD=90°(直角三角形中两个锐角互余)
∴∠BCD=∠A (同角的余角相等)
又∵∠EBC=∠A(已知)
∴∠EBC=∠BCD
∴BE∥CD( 内错角相等,两直线平行)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
