1.3 证明(2) 课件(共18张PPT)
文档属性
| 名称 | 1.3 证明(2) 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 18:54:46 | ||
图片预览


文档简介
(共18张PPT)
1.3 证明(2)
浙教版八年级上册
A
B
C
D
E
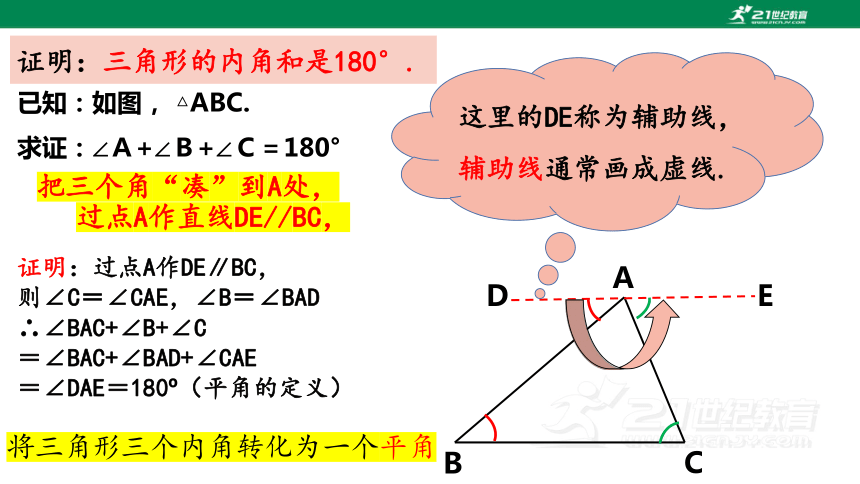
这里的DE称为辅助线,辅助线通常画成虚线.
证明:三角形的内角和是180°.
证明:过点A作DE∥BC,
则∠C=∠CAE,∠B=∠BAD
∴∠BAC+∠B+∠C
=∠BAC+∠BAD+∠CAE
=∠DAE=180 (平角的定义)
已知:如图, △ABC.
求证:∠A+∠B+∠C=180°
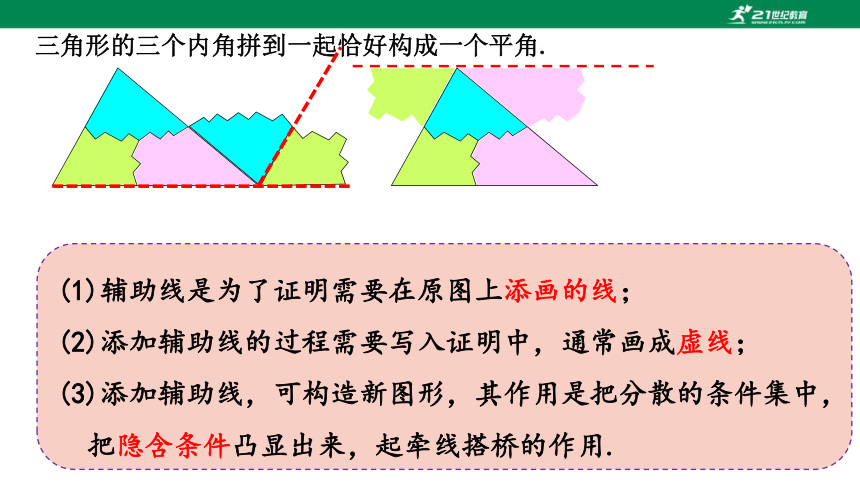
三角形的三个内角拼到一起恰好构成一个平角.
(1)辅助线是为了证明需要在原图上添画的线;
(2)添加辅助线的过程需要写入证明中,通常画成虚线;
(3)添加辅助线,可构造新图形,其作用是把分散的条件集中,把隐含条件凸显出来,起牵线搭桥的作用.
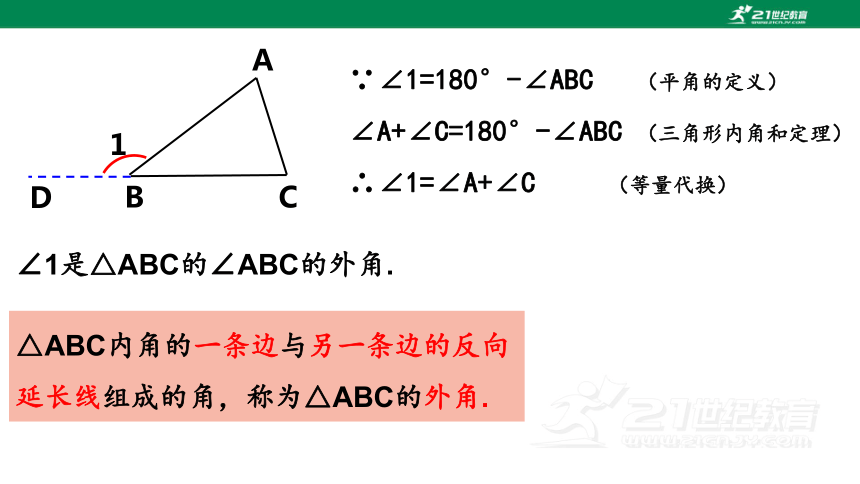
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.
B
C
A
1
D
∠1是△ABC的∠ABC的外角.
∵∠1=180°-∠ABC (平角的定义) ∠A+∠C=180°-∠ABC (三角形内角和定理)
∴∠1=∠A+∠C (等量代换)
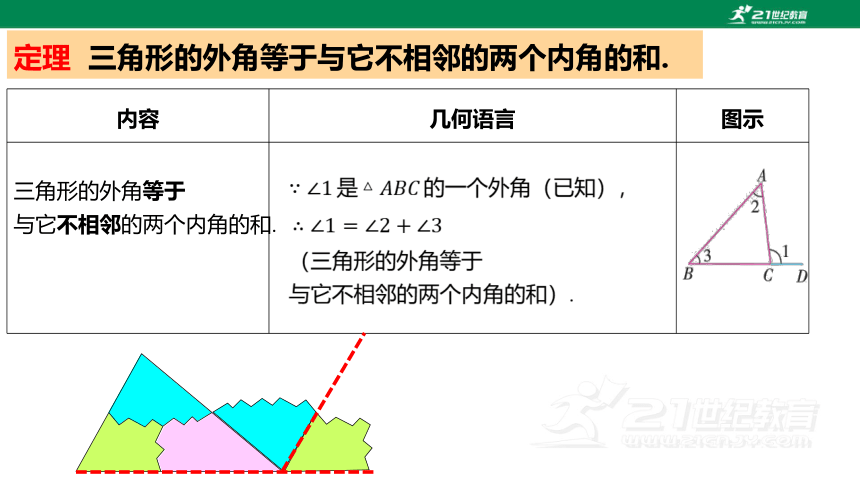
三角形的外角等于
与它不相邻的两个内角的和.
定理 三角形的外角等于与它不相邻的两个内角的和.
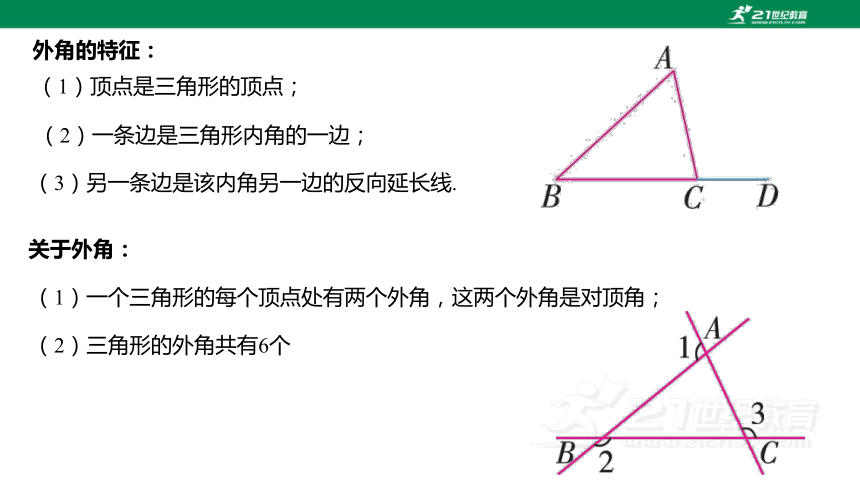
(1)一个三角形的每个顶点处有两个外角,这两个外角是对顶角;
(2)三角形的外角共有6个
外角的特征:
(2)一条边是三角形内角的一边;
(3)另一条边是该内角另一边的反向延长线.
关于外角:
(1)顶点是三角形的顶点;
猜想:“三角形不共顶点的三个外角的和等于 0”
B
C
A
1
2
3
4
5
6
已知:△ABC的三个内角分别为∠1、 ∠2、 ∠3,
相对应的外角为∠4、 ∠5、 ∠6.
求证: ∠4+∠5+∠6=360°.
证明:∵∠4=∠2+∠3,∠5=∠1+∠3, ∠6=∠1+∠2
(三角形的外角等于与它不相邻的两个内角的和),
∴∠4+∠5+∠6
=2(∠1+∠2+∠3)
=2×180°
=360°.
∠2=∠A+ ∠B
不相邻内角
2
C
A
B
.
D
1
外角
相邻内角
∠2﹥∠A
∠2﹥∠B
证明几何命题时,表述格式一般是:
(1)按题意画出图形。
(2)分清命题的条件和结论,结合图形,
在“已知”中写出条件,在“求证”中写出结论.
(3)在“证明”中写出推理过程.
已知:如图,∠B+∠D= ∠BCD.求证:AB∥DE.
A
B
D
E
C
F
证明:延长BC,交DE于点F.
∵ ∠B+∠D= ∠BCD(已知),
又∵ ∠BCD=∠D+∠CFD
(三角形的外角等于与它不相邻的两个内角的和)
∴ ∠B+∠D=∠D+∠CFD,
∴ ∠B=∠CFD,
∴AB∥DE(内错角相等,两直线平行).
3.已知:如图,O为△ABC内任意一点.
求证:∠BOC=∠1+∠2+∠A.
提示:延长BO,交AC于点D.
依据“三角形的外角等于与它不相邻的两个内角的和”,得∠BOC=∠ODC+∠2=∠1+∠A+∠2.
已知
高线的定义
三角形的外角等于与它不相邻的两个内角的和
5.一张小凳子的结构如图所示,
∠1=∠2,∠3=100°.
求∠1的度数.
答案:50°.
6.如图,在五角星图形中,
求:∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
解:如右图所示, ∵∠1=∠C+∠2,∠2=∠A+∠D, ∴∠1=∠C+∠A+∠D, 又∵∠1+∠B+∠E=180°, ∴∠A+∠B+∠C+∠D+∠E=180°.
7.计算:∠A+∠B+∠C+∠D+∠E+∠F=______度.
360
A
B
C
E
D
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3 证明(2)
浙教版八年级上册
A
B
C
D
E
这里的DE称为辅助线,辅助线通常画成虚线.
证明:三角形的内角和是180°.
证明:过点A作DE∥BC,
则∠C=∠CAE,∠B=∠BAD
∴∠BAC+∠B+∠C
=∠BAC+∠BAD+∠CAE
=∠DAE=180 (平角的定义)
已知:如图, △ABC.
求证:∠A+∠B+∠C=180°
三角形的三个内角拼到一起恰好构成一个平角.
(1)辅助线是为了证明需要在原图上添画的线;
(2)添加辅助线的过程需要写入证明中,通常画成虚线;
(3)添加辅助线,可构造新图形,其作用是把分散的条件集中,把隐含条件凸显出来,起牵线搭桥的作用.
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.
B
C
A
1
D
∠1是△ABC的∠ABC的外角.
∵∠1=180°-∠ABC (平角的定义) ∠A+∠C=180°-∠ABC (三角形内角和定理)
∴∠1=∠A+∠C (等量代换)
三角形的外角等于
与它不相邻的两个内角的和.
定理 三角形的外角等于与它不相邻的两个内角的和.
(1)一个三角形的每个顶点处有两个外角,这两个外角是对顶角;
(2)三角形的外角共有6个
外角的特征:
(2)一条边是三角形内角的一边;
(3)另一条边是该内角另一边的反向延长线.
关于外角:
(1)顶点是三角形的顶点;
猜想:“三角形不共顶点的三个外角的和等于 0”
B
C
A
1
2
3
4
5
6
已知:△ABC的三个内角分别为∠1、 ∠2、 ∠3,
相对应的外角为∠4、 ∠5、 ∠6.
求证: ∠4+∠5+∠6=360°.
证明:∵∠4=∠2+∠3,∠5=∠1+∠3, ∠6=∠1+∠2
(三角形的外角等于与它不相邻的两个内角的和),
∴∠4+∠5+∠6
=2(∠1+∠2+∠3)
=2×180°
=360°.
∠2=∠A+ ∠B
不相邻内角
2
C
A
B
.
D
1
外角
相邻内角
∠2﹥∠A
∠2﹥∠B
证明几何命题时,表述格式一般是:
(1)按题意画出图形。
(2)分清命题的条件和结论,结合图形,
在“已知”中写出条件,在“求证”中写出结论.
(3)在“证明”中写出推理过程.
已知:如图,∠B+∠D= ∠BCD.求证:AB∥DE.
A
B
D
E
C
F
证明:延长BC,交DE于点F.
∵ ∠B+∠D= ∠BCD(已知),
又∵ ∠BCD=∠D+∠CFD
(三角形的外角等于与它不相邻的两个内角的和)
∴ ∠B+∠D=∠D+∠CFD,
∴ ∠B=∠CFD,
∴AB∥DE(内错角相等,两直线平行).
3.已知:如图,O为△ABC内任意一点.
求证:∠BOC=∠1+∠2+∠A.
提示:延长BO,交AC于点D.
依据“三角形的外角等于与它不相邻的两个内角的和”,得∠BOC=∠ODC+∠2=∠1+∠A+∠2.
已知
高线的定义
三角形的外角等于与它不相邻的两个内角的和
5.一张小凳子的结构如图所示,
∠1=∠2,∠3=100°.
求∠1的度数.
答案:50°.
6.如图,在五角星图形中,
求:∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
解:如右图所示, ∵∠1=∠C+∠2,∠2=∠A+∠D, ∴∠1=∠C+∠A+∠D, 又∵∠1+∠B+∠E=180°, ∴∠A+∠B+∠C+∠D+∠E=180°.
7.计算:∠A+∠B+∠C+∠D+∠E+∠F=______度.
360
A
B
C
E
D
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
