1.5全等三角形的判定(1) 课件(共22张PPT)
文档属性
| 名称 | 1.5全等三角形的判定(1) 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 18:56:36 | ||
图片预览




文档简介
(共22张PPT)
1.5 全等三角形的判定(1)
浙教版八年级上册
温故知新
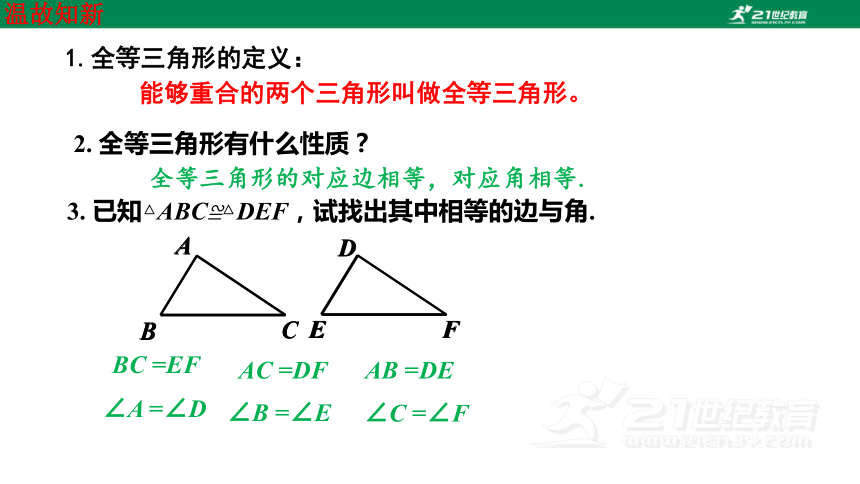
2. 全等三角形有什么性质?
∠A =∠D
AB =DE
∠B =∠E
BC =EF
∠C =∠F
AC =DF
A
B
C
D
E
F
全等三角形的对应边相等,对应角相等.
3. 已知△ABC≌△DEF,试找出其中相等的边与角.
A
B
C
D
E
F
1.全等三角形的定义:
能够重合的两个三角形叫做全等三角形。
根据定义判定两个三角形全等,需要知道哪些条件
三条边对应相等,三个角对应相等.
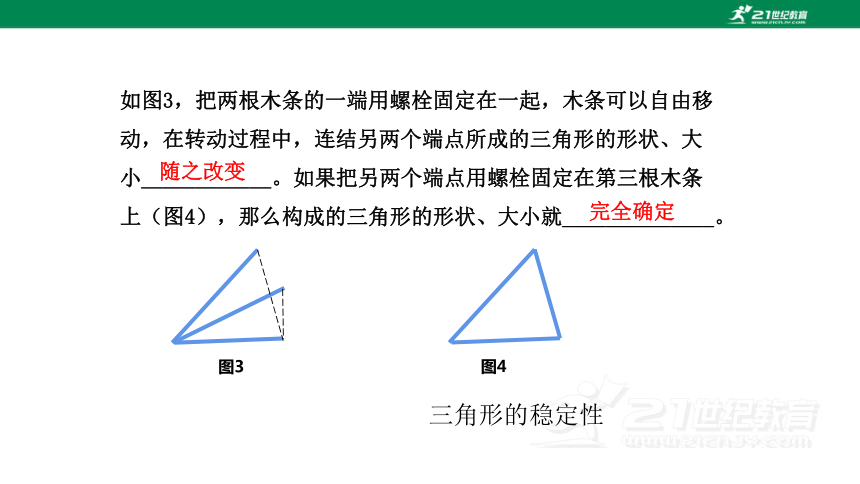
如图3,把两根木条的一端用螺栓固定在一起,木条可以自由移动,在转动过程中,连结另两个端点所成的三角形的形状、大小____________。如果把另两个端点用螺栓固定在第三根木条上(图4),那么构成的三角形的形状、大小就______________。
图3
图4
随之改变
完全确定
三角形的稳定性
三角形的稳定性在生产和日常生活中有广泛的应用.例如,房屋的人字架、大桥的钢梁、起重机的支架等,都采用三角形结构,以起到稳固的作用.
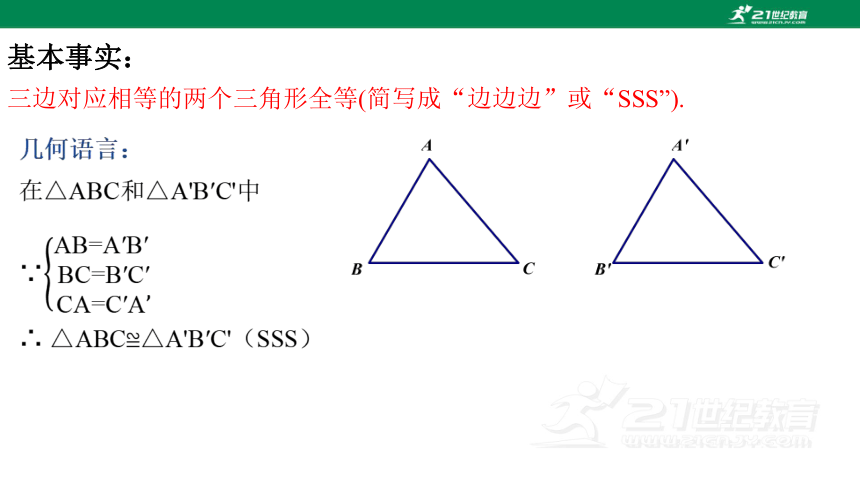
基本事实:
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
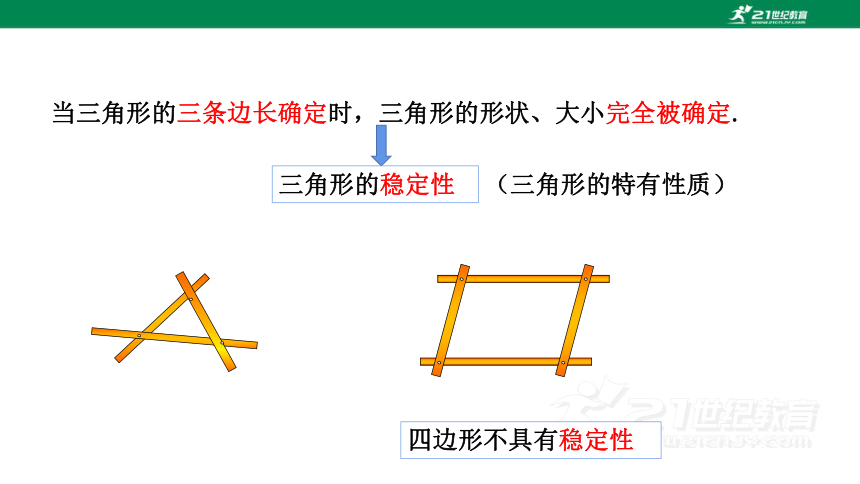
当三角形的三条边长确定时,三角形的形状、大小完全被确定.
三角形的稳定性
(三角形的特有性质)
四边形不具有稳定性
画一个三角形,三边长分别为3cm,4cm,5cm
4
3
5
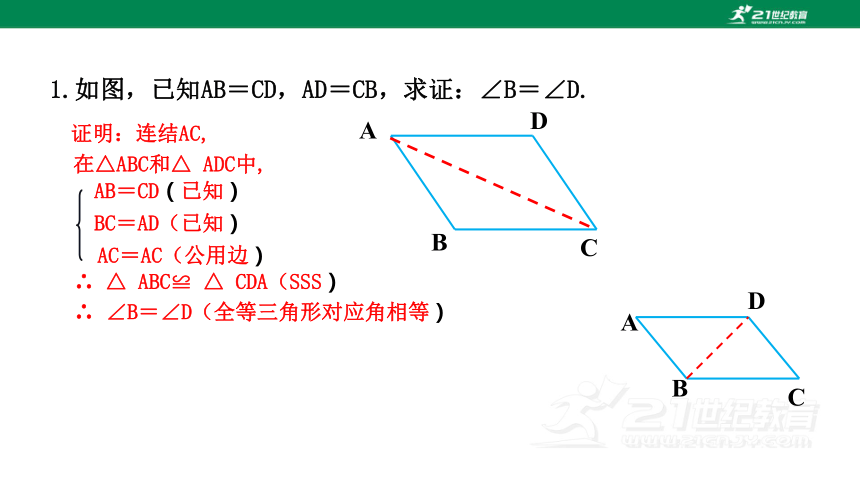
1.如图,已知AB=CD,AD=CB,求证:∠B=∠D.
证明:连结AC,
∴ △ ABC≌ △ CDA(SSS)
∴ ∠B=∠D(全等三角形对应角相等)
A
B
C
D
A
B
C
D
AB=CD(已知)
AC=AC(公用边)
BC=AD(已知)
在△ABC和△ ADC中,
例2已知∠AOB, 求作∠A′O′B′,使∠A′O′B′=∠AOB.
作法:
1.以点O为圆心,适当长为半径画弧, 分别交OA,OB于点C,D.
2.画一条射线O′A′,以点O′为圆心,
OC长为半径画弧l,O′A′于点C′.
3.以点C′为圆心,
CD长为半径画弧,交弧l点D′.
4.过点D′画射线O′B′.
结论:∠A′O′B′就是所求作的角
O
A
B
A′
B′
O′
C
D
C′
D′
l
证明:连结CD和C′ D′,
∴∠A′O′B′=∠AOB.
O
A
B
A′
B′
O′
C
D
C′
D′
l
OC= O′ C′
OD= O′ D′
CD= C′ D′
∴△OCD≌△O′ C′ D′(SSS)
在△OCD与△O′ C′ D′中
例3。过直线外一点,作已知直线的平行线
P
m
Q
M
N
H
K
结论:直线KP就是直线m的平行线.
例3.过直线外一点P,作已知直线m的平行线
P
m
Q
M
N
H
K
结论:直线KP就是直线m的平行线.
D
1.如图,建筑工人砌墙,在加入门框时,常用木条EF固定长方形门框ABCD, 使其不变形,这种做法是利用( )
A.长方形的四个角都是直角 B.两点之间线段最短
C.长方形的对称性 D.三角形的稳定性
当堂检测:
2.如图,C是AE的中点,AB=CD,CB=ED.求证:AB∥CD.
3. 已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
解:连结AB.
在△ACB 和 △ADB中,
∴△ACB≌△ADB(SSS)
A
B
C
D
∴∠C=∠D
(全等三角形对应角相等).
AC = AD
BC = BD ,
AB = AB (公共边)
4. 如图,点B, E, C, F在同一条直线上, 且AB=DE, AC=DF, BE=CF.求证:△ABC ≌△DEF.
A
D
B
E
C
F
证明: ∵BE=CF ( )
∴BE+EC=CF+EC
∴BC=EF
在△ABC和△DEF中,
∴△ABC≌△DEF ( )
AB=___ ( )
___=DF ( )
BC=__ ( )
已知
已知
DE
AC
EF
已知
已证
SSS
5.已知:如图,AB=DE,BC=EF,AF=DC.求证:BC∥EF.
提示:由已知可得△ABC≌△DEF(SSS),
∴ ∠EFD=∠BCA(全等三角形的对应角相等),
∴ ∠EFC=∠BCA(等角的补角相等),
∴ EF∥BC(内错角相等,两直线平行).
6.如图,△ABC和△DBC中,AB=CD,AC=BD,AC和DB相交于O,说出∠1=∠2的理由.
AB=CD
AC=BD
BC=CB
∴
△ABC≌△DCB
∴∠ABC=∠DCB,
∠ACB=∠DBC
即∠1=∠2
解:
(已知)
(公共边)
(已知)
(SSS)
(全等三角形对应角相等)
∴∠ABC-∠DBC
=∠DCB-∠ACB,
A
B
C
D
O
2
1
在△ABC和△DCB中
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5 全等三角形的判定(1)
浙教版八年级上册
温故知新
2. 全等三角形有什么性质?
∠A =∠D
AB =DE
∠B =∠E
BC =EF
∠C =∠F
AC =DF
A
B
C
D
E
F
全等三角形的对应边相等,对应角相等.
3. 已知△ABC≌△DEF,试找出其中相等的边与角.
A
B
C
D
E
F
1.全等三角形的定义:
能够重合的两个三角形叫做全等三角形。
根据定义判定两个三角形全等,需要知道哪些条件
三条边对应相等,三个角对应相等.
如图3,把两根木条的一端用螺栓固定在一起,木条可以自由移动,在转动过程中,连结另两个端点所成的三角形的形状、大小____________。如果把另两个端点用螺栓固定在第三根木条上(图4),那么构成的三角形的形状、大小就______________。
图3
图4
随之改变
完全确定
三角形的稳定性
三角形的稳定性在生产和日常生活中有广泛的应用.例如,房屋的人字架、大桥的钢梁、起重机的支架等,都采用三角形结构,以起到稳固的作用.
基本事实:
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
当三角形的三条边长确定时,三角形的形状、大小完全被确定.
三角形的稳定性
(三角形的特有性质)
四边形不具有稳定性
画一个三角形,三边长分别为3cm,4cm,5cm
4
3
5
1.如图,已知AB=CD,AD=CB,求证:∠B=∠D.
证明:连结AC,
∴ △ ABC≌ △ CDA(SSS)
∴ ∠B=∠D(全等三角形对应角相等)
A
B
C
D
A
B
C
D
AB=CD(已知)
AC=AC(公用边)
BC=AD(已知)
在△ABC和△ ADC中,
例2已知∠AOB, 求作∠A′O′B′,使∠A′O′B′=∠AOB.
作法:
1.以点O为圆心,适当长为半径画弧, 分别交OA,OB于点C,D.
2.画一条射线O′A′,以点O′为圆心,
OC长为半径画弧l,O′A′于点C′.
3.以点C′为圆心,
CD长为半径画弧,交弧l点D′.
4.过点D′画射线O′B′.
结论:∠A′O′B′就是所求作的角
O
A
B
A′
B′
O′
C
D
C′
D′
l
证明:连结CD和C′ D′,
∴∠A′O′B′=∠AOB.
O
A
B
A′
B′
O′
C
D
C′
D′
l
OC= O′ C′
OD= O′ D′
CD= C′ D′
∴△OCD≌△O′ C′ D′(SSS)
在△OCD与△O′ C′ D′中
例3。过直线外一点,作已知直线的平行线
P
m
Q
M
N
H
K
结论:直线KP就是直线m的平行线.
例3.过直线外一点P,作已知直线m的平行线
P
m
Q
M
N
H
K
结论:直线KP就是直线m的平行线.
D
1.如图,建筑工人砌墙,在加入门框时,常用木条EF固定长方形门框ABCD, 使其不变形,这种做法是利用( )
A.长方形的四个角都是直角 B.两点之间线段最短
C.长方形的对称性 D.三角形的稳定性
当堂检测:
2.如图,C是AE的中点,AB=CD,CB=ED.求证:AB∥CD.
3. 已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
解:连结AB.
在△ACB 和 △ADB中,
∴△ACB≌△ADB(SSS)
A
B
C
D
∴∠C=∠D
(全等三角形对应角相等).
AC = AD
BC = BD ,
AB = AB (公共边)
4. 如图,点B, E, C, F在同一条直线上, 且AB=DE, AC=DF, BE=CF.求证:△ABC ≌△DEF.
A
D
B
E
C
F
证明: ∵BE=CF ( )
∴BE+EC=CF+EC
∴BC=EF
在△ABC和△DEF中,
∴△ABC≌△DEF ( )
AB=___ ( )
___=DF ( )
BC=__ ( )
已知
已知
DE
AC
EF
已知
已证
SSS
5.已知:如图,AB=DE,BC=EF,AF=DC.求证:BC∥EF.
提示:由已知可得△ABC≌△DEF(SSS),
∴ ∠EFD=∠BCA(全等三角形的对应角相等),
∴ ∠EFC=∠BCA(等角的补角相等),
∴ EF∥BC(内错角相等,两直线平行).
6.如图,△ABC和△DBC中,AB=CD,AC=BD,AC和DB相交于O,说出∠1=∠2的理由.
AB=CD
AC=BD
BC=CB
∴
△ABC≌△DCB
∴∠ABC=∠DCB,
∠ACB=∠DBC
即∠1=∠2
解:
(已知)
(公共边)
(已知)
(SSS)
(全等三角形对应角相等)
∴∠ABC-∠DBC
=∠DCB-∠ACB,
A
B
C
D
O
2
1
在△ABC和△DCB中
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
