1.5全等三角形的判定(2) 课件(共19张PPT)
文档属性
| 名称 | 1.5全等三角形的判定(2) 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 18:57:05 | ||
图片预览



文档简介
(共19张PPT)
1.5 全等三角形的判定(2)
浙教版八年级上册
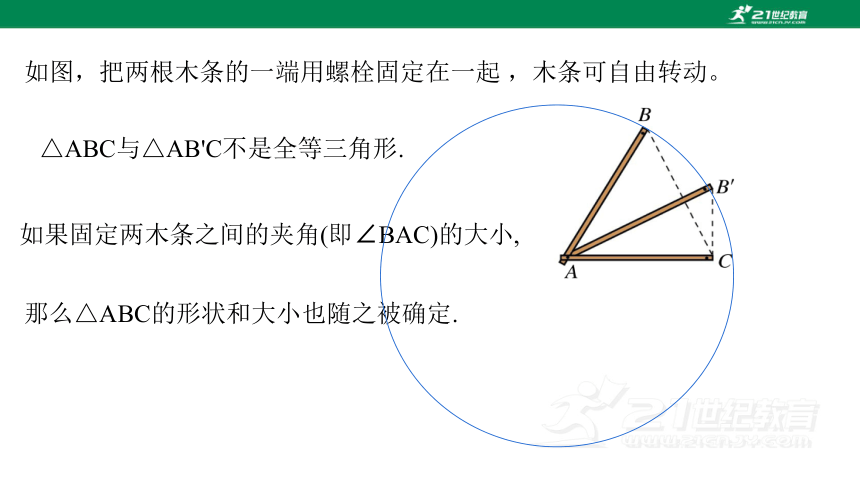
如图,把两根木条的一端用螺栓固定在一起 ,木条可自由转动。
△ABC与△AB'C不是全等三角形.
如果固定两木条之间的夹角(即∠BAC)的大小,
那么△ABC的形状和大小也随之被确定.
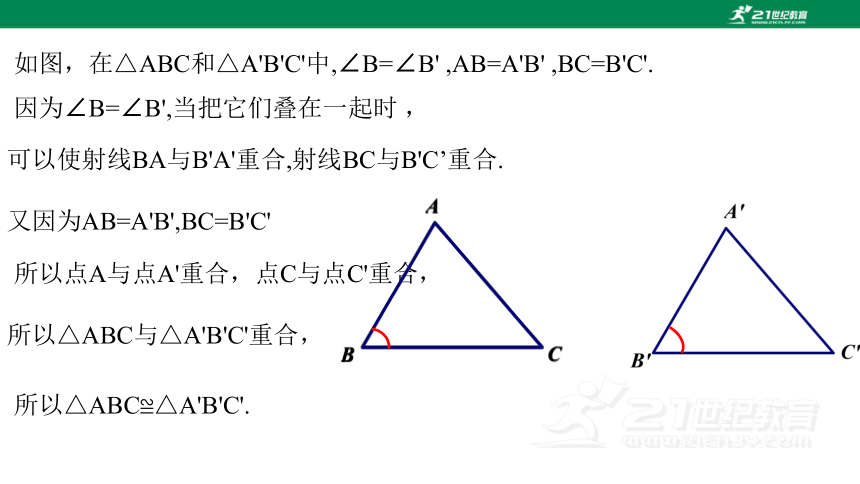
如图,在△ABC和△A'B'C'中,∠B=∠B' ,AB=A'B' ,BC=B'C'.
又因为AB=A'B',BC=B'C'
因为∠B=∠B',当把它们叠在一起时 ,
可以使射线BA与B'A'重合,射线BC与B'C’重合.
所以点A与点A'重合,点C与点C'重合,
所以△ABC与△A'B'C'重合,
所以△ABC≌△A'B'C'.
两边及其夹角分别相等的两个三角形全等.
简称“边角边”和“SAS”.
在△ABC与△DEF中,
∴△ABC≌△DEF(SAS).
A
B
C
D
E
F
基本事实:
几何语言:
例4.已知:如图,AB与CD相交于点0,且OA=OB,OC=OD.
求证: △AOC≌△BOD.
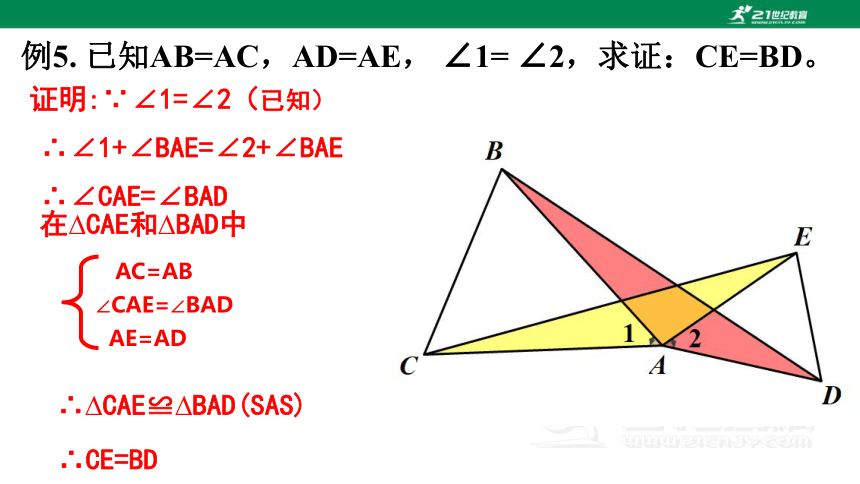
例5. 已知AB=AC,AD=AE, ∠1= ∠2,求证:CE=BD。
证明:∵∠1=∠2(已知)
∴∠1+∠BAE=∠2+∠BAE
∴∠CAE=∠BAD
在 CAE和 BAD中
∴ CAE≌ BAD(SAS)
∴CE=BD
AC=AB
∠CAE=∠BAD
AE=AD
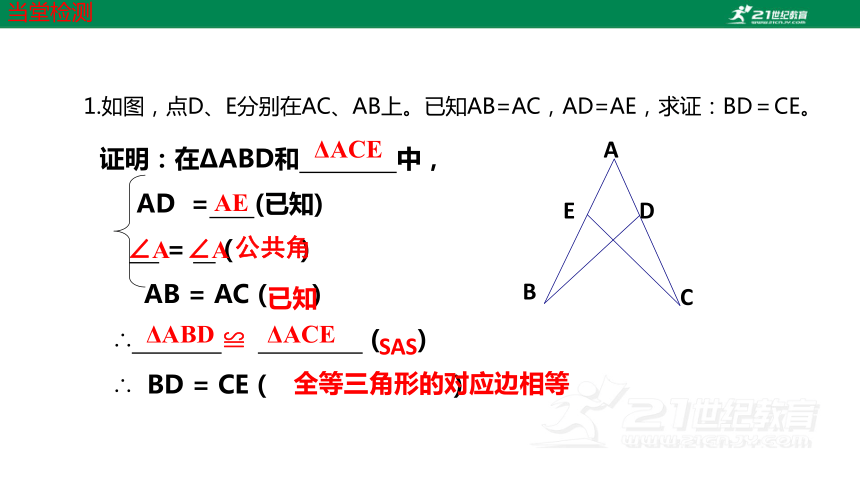
1.如图,点D、E分别在AC、AB上。已知AB=AC,AD=AE,求证:BD=CE。
证明:在ΔABD和 中,
AD = (已知)
= ( )
AB = AC( )
∴ ≌ ( )
∴ BD = CE( )
ΔACE
AE
∠A
∠A
已知
ΔABD
ΔACE
SAS
全等三角形的对应边相等
A
E
D
B
C
公共角
当堂检测
2.如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。说明卡钳的工作原理。
此工具是根据三角形全等制作而成的. ∵O是AA′,BB′的中点,∴AO=A′O,BO=B′O, ∴∠AOB=∠A′OB′(对顶角相等) 在△AOB和△A′OB′中, ∵ AO=A′O, ∠AOB=∠A′OB′,
BO=B′O, ∴△AOB≌△A′OB′(SAS), ∴A′B′=AB,
∴只要量出A′B′的长度,就可以测量工件内槽宽的卡钳
3.动手操作:画出一个角为45°,
角的对边为5cm,角的一条邻边为6cm的三角形,
与同桌互相比较所画的三角形,它们能重合吗?
两边及其一边所对的角相等,两个三角形不一定全等
必须是两边及其夹角对应相等
“SSA”( × )
(1)两边及其夹角;
(2)两边及一边的对角.
A
B
C
SSA不能判定全等.
SAS能判定全等.
4.如图线段AB是一个池塘的长度,现在想测量这个池塘的长度,
在水上测量不方便,你有什么好的方法较方便地把池塘的长度测量出来吗?想想看。
设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。
AC=DC
∠ACB=∠DCE
BC=EC
∴ △ACB≌△DCE(SAS)
∴ AB=DE
E
C
B
A
D
∵ 在△ACB和△DCE中,
5.如图,已知AB=AD, AC=AE ,∠1=∠2,
求证: ∠B=∠D
A
B
C
D
E
1
2
证明:∵∠1=∠2(已知)
∴∠1+∠EAC=∠2+∠EAC
∴∠BAC=∠DAE
在 ABC和 ADE中
∴ ABC≌ ADE(SAS)
∴∠B=∠D
6.如图所示,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC 于点G.求证:DF∥BC
(1)∵AF平分∠CAB,∴∠CAF=∠DAF.
在△ACF和△ADF中,∵
∴△ACF≌△ADF(SAS).∴∠ACF=∠ADF.
∵CE⊥AB,∠ACB=90°
∴∠ACE+∠CAE=90°,∠CAE+∠B=90°
∴∠ACF=∠B∴∠ADF=∠B.∴DF∥BC.
7.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:延长AD至点E,使DE=AD,连结BE.
∵D为BC的中点,∴CD=BD.
又∵AD=ED,∠ADC=∠EDB,∴△ADC≌△EDB.
∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作BE//AC交AD的延长线于点E
∠ACD=∠EBD,∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作∠ACD=∠EBD交AD的延长线于点E,
∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.
∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
数学源于生活,
又反过来服务于生活.
如果你无愧于数学,
那数学就可以助你到达胜利的彼岸.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5 全等三角形的判定(2)
浙教版八年级上册
如图,把两根木条的一端用螺栓固定在一起 ,木条可自由转动。
△ABC与△AB'C不是全等三角形.
如果固定两木条之间的夹角(即∠BAC)的大小,
那么△ABC的形状和大小也随之被确定.
如图,在△ABC和△A'B'C'中,∠B=∠B' ,AB=A'B' ,BC=B'C'.
又因为AB=A'B',BC=B'C'
因为∠B=∠B',当把它们叠在一起时 ,
可以使射线BA与B'A'重合,射线BC与B'C’重合.
所以点A与点A'重合,点C与点C'重合,
所以△ABC与△A'B'C'重合,
所以△ABC≌△A'B'C'.
两边及其夹角分别相等的两个三角形全等.
简称“边角边”和“SAS”.
在△ABC与△DEF中,
∴△ABC≌△DEF(SAS).
A
B
C
D
E
F
基本事实:
几何语言:
例4.已知:如图,AB与CD相交于点0,且OA=OB,OC=OD.
求证: △AOC≌△BOD.
例5. 已知AB=AC,AD=AE, ∠1= ∠2,求证:CE=BD。
证明:∵∠1=∠2(已知)
∴∠1+∠BAE=∠2+∠BAE
∴∠CAE=∠BAD
在 CAE和 BAD中
∴ CAE≌ BAD(SAS)
∴CE=BD
AC=AB
∠CAE=∠BAD
AE=AD
1.如图,点D、E分别在AC、AB上。已知AB=AC,AD=AE,求证:BD=CE。
证明:在ΔABD和 中,
AD = (已知)
= ( )
AB = AC( )
∴ ≌ ( )
∴ BD = CE( )
ΔACE
AE
∠A
∠A
已知
ΔABD
ΔACE
SAS
全等三角形的对应边相等
A
E
D
B
C
公共角
当堂检测
2.如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。说明卡钳的工作原理。
此工具是根据三角形全等制作而成的. ∵O是AA′,BB′的中点,∴AO=A′O,BO=B′O, ∴∠AOB=∠A′OB′(对顶角相等) 在△AOB和△A′OB′中, ∵ AO=A′O, ∠AOB=∠A′OB′,
BO=B′O, ∴△AOB≌△A′OB′(SAS), ∴A′B′=AB,
∴只要量出A′B′的长度,就可以测量工件内槽宽的卡钳
3.动手操作:画出一个角为45°,
角的对边为5cm,角的一条邻边为6cm的三角形,
与同桌互相比较所画的三角形,它们能重合吗?
两边及其一边所对的角相等,两个三角形不一定全等
必须是两边及其夹角对应相等
“SSA”( × )
(1)两边及其夹角;
(2)两边及一边的对角.
A
B
C
SSA不能判定全等.
SAS能判定全等.
4.如图线段AB是一个池塘的长度,现在想测量这个池塘的长度,
在水上测量不方便,你有什么好的方法较方便地把池塘的长度测量出来吗?想想看。
设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。
AC=DC
∠ACB=∠DCE
BC=EC
∴ △ACB≌△DCE(SAS)
∴ AB=DE
E
C
B
A
D
∵ 在△ACB和△DCE中,
5.如图,已知AB=AD, AC=AE ,∠1=∠2,
求证: ∠B=∠D
A
B
C
D
E
1
2
证明:∵∠1=∠2(已知)
∴∠1+∠EAC=∠2+∠EAC
∴∠BAC=∠DAE
在 ABC和 ADE中
∴ ABC≌ ADE(SAS)
∴∠B=∠D
6.如图所示,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC 于点G.求证:DF∥BC
(1)∵AF平分∠CAB,∴∠CAF=∠DAF.
在△ACF和△ADF中,∵
∴△ACF≌△ADF(SAS).∴∠ACF=∠ADF.
∵CE⊥AB,∠ACB=90°
∴∠ACE+∠CAE=90°,∠CAE+∠B=90°
∴∠ACF=∠B∴∠ADF=∠B.∴DF∥BC.
7.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:延长AD至点E,使DE=AD,连结BE.
∵D为BC的中点,∴CD=BD.
又∵AD=ED,∠ADC=∠EDB,∴△ADC≌△EDB.
∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作BE//AC交AD的延长线于点E
∠ACD=∠EBD,∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作∠ACD=∠EBD交AD的延长线于点E,
∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.
∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
数学源于生活,
又反过来服务于生活.
如果你无愧于数学,
那数学就可以助你到达胜利的彼岸.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
