1.5全等三角形的判定(3) 课件(共21张PPT)
文档属性
| 名称 | 1.5全等三角形的判定(3) 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
1.5全等三角形的判定(3)
浙教版八年级上册
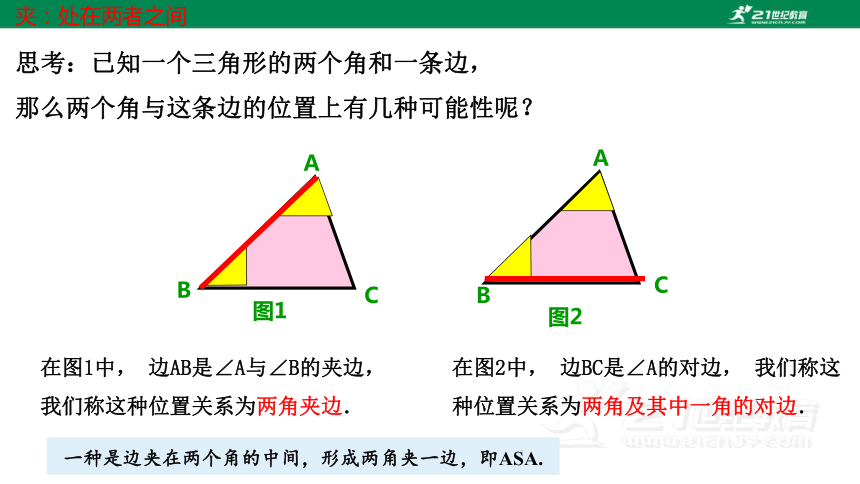
思考:已知一个三角形的两个角和一条边,
那么两个角与这条边的位置上有几种可能性呢?
A
B
C
A
B
C
图1
图2
在图1中, 边AB是∠A与∠B的夹边, 我们称这种位置关系为两角夹边.
在图2中, 边BC是∠A的对边, 我们称这种位置关系为两角及其中一角的对边.
一种是边夹在两个角的中间,形成两角夹一边,即ASA.
夹:处在两者之间
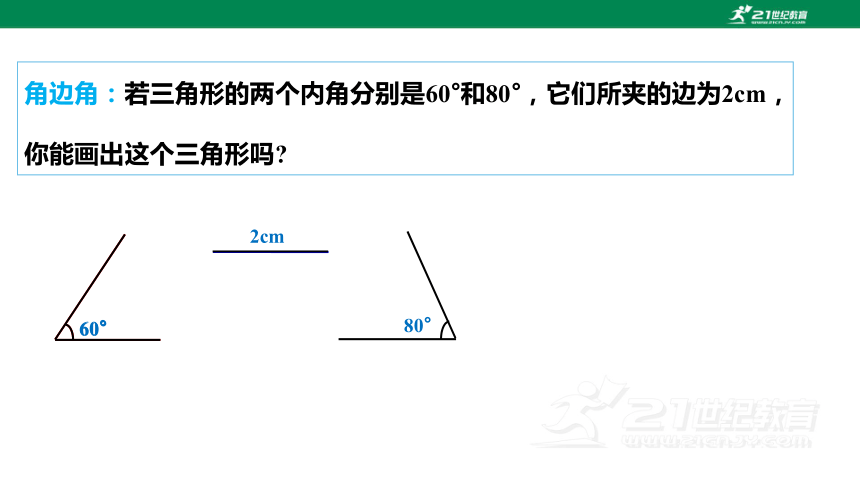
角边角:若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,
你能画出这个三角形吗
80°
2cm
60°
60°
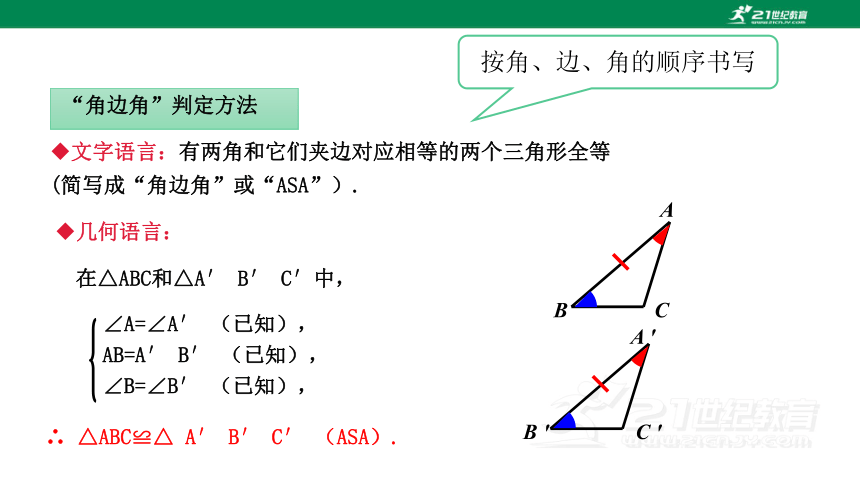
“角边角”判定方法
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
按角、边、角的顺序书写
1.如图,某同学不小心将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,最省事的办法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
C
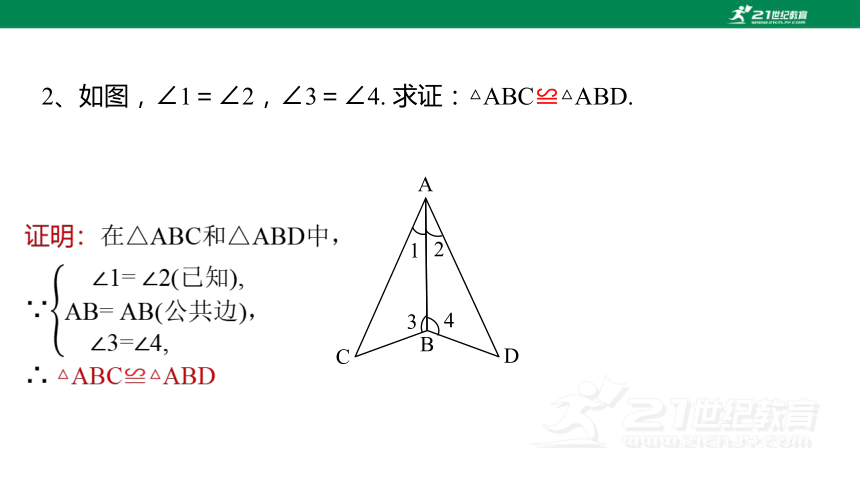
2、如图,∠1=∠2,∠3=∠4. 求证:△ABC≌△ABD.
A
C
B
D
1
2
3
4
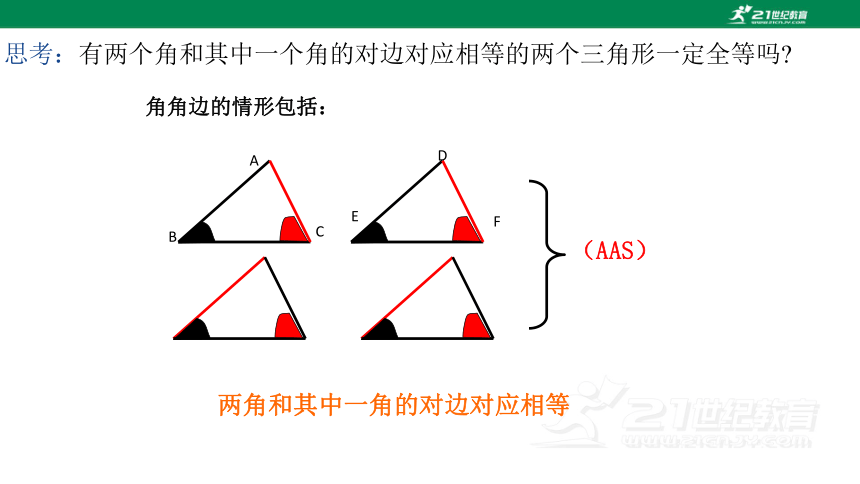
(AAS)
A
B
C
D
E
F
角角边的情形包括:
两角和其中一角的对边对应相等
思考:有两个角和其中一个角的对边对应相等的两个三角形一定全等吗
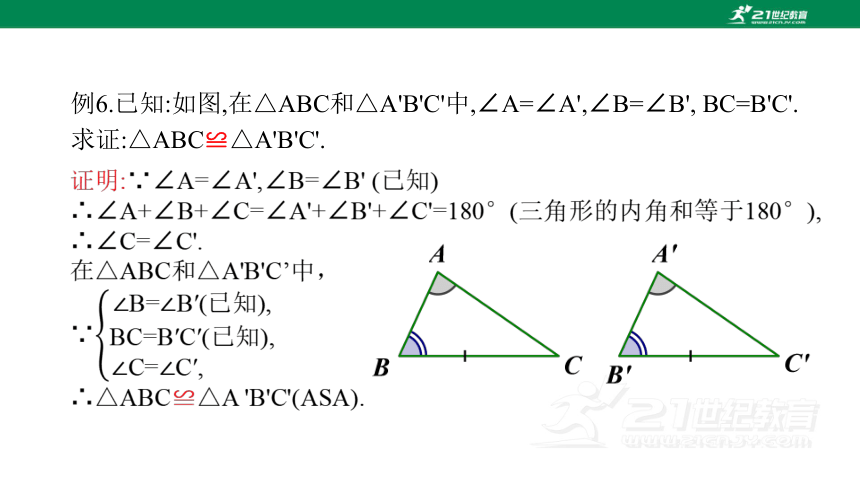
例6.已知:如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B', BC=B'C'.
求证:△ABC≌△A'B'C'.
两角及其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
按角、角、边的顺序书写
能不能把“AAS”、“ASA”简述为
“两角和一边对应相等的两个三角形全等”?
A
B
C
D
E
在△ADE和△ABC中
但△ABC和△ADE不全等
结论:说明两个三角形全等时,特别注意边和角“位置上对应相等”.
例如:
其中一个角的对边对应相等
SSS
SAS
A
B
C
D
E
F
A
B
C
D
E
F
(1)
(2)
ASA
AAS
(3)
(4)
A
B
C
D
E
F
A
B
C
D
E
F
两个三角形全等
的判定条件
例7.已知∠BAC=∠ABD,∠ABC=∠DAB.
求证:AO=CO,BP=CP
∠D=∠C
∴AO=CO,BP=CP
∠D=∠C
∠OAD=∠OBC
AD= BC
∴△OAD≌△OBC(AAS)
在△OAD与△O BC中
在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC (已知)
∠A=∠A(公共角)
∴ △ABD≌△ACE (ASA)
∴AE=AD
1. 已知:AB=AC,∠B=∠C,
求证:AE=AD
A
B
D
C
E
证明:
当堂检测:
1
2
3
4
D
A
B
C
2.如图,∠1=∠2,∠3=∠4,说明:AC=AD
解:∵∠ =180 -∠3
∠ =180 -∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ 和△ 中
( )
(公共边)
( )
∴△ ≌ △ ( )
∴ (全等三角形对应边相等)
ABD
ABC
ABC
∠1=∠2
AB=AB
∠ABD=∠ABC
ASA
AC=AD
ABD
已知
已证
ABC
ABD
3.已知:如图,AD平分∠BAC,______________.
求证:BD=CD.
(请在横线上添加一个条件,使得结论成立)
思路①:根据SAS,添加
思路②:根据ASA,添加
思路③:根据AAS,添加
AB=AC
∠ ADB=∠ADC
∠B= ∠C
4.已知:如图,∠1=∠2,∠C=∠E,AC=AE.
求证:△ABC≌△ADE.
阅读下面一段文字:
泰勒斯(Thales,约公元前625~前547年)是古希腊哲学家.相传"两个角及其夹边对应相等的两个三角形全等"就是由泰勒斯首先提出的.泰勒斯利用这个判定三角形全等的依据求出了岸上一点到海中一艘船的距离.
如图,A是观察点,船P在A的正前方.过A作AP的垂线 l, 在垂线l上截取任意长AB,O 是AB 的中点.观测者从点B沿垂直于AB的BK方向走,直到点K,船P和点O在一条直线上,那么BK的距离即为船离岸的距离.请给出证明.
证明:∵AD∥BC∴∠ADB=∠CBD
∵AB∥CD∴∠ABD=∠CDB
A
B
C
D
6.已知:AB//CD,AD∥BC。
求证:△ABD≌△CDB
7.如图,已知EC=AC,∠BCE=∠ACD,∠A=∠E.求证:△ACB≌△ECD
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5全等三角形的判定(3)
浙教版八年级上册
思考:已知一个三角形的两个角和一条边,
那么两个角与这条边的位置上有几种可能性呢?
A
B
C
A
B
C
图1
图2
在图1中, 边AB是∠A与∠B的夹边, 我们称这种位置关系为两角夹边.
在图2中, 边BC是∠A的对边, 我们称这种位置关系为两角及其中一角的对边.
一种是边夹在两个角的中间,形成两角夹一边,即ASA.
夹:处在两者之间
角边角:若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,
你能画出这个三角形吗
80°
2cm
60°
60°
“角边角”判定方法
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
按角、边、角的顺序书写
1.如图,某同学不小心将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,最省事的办法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
C
2、如图,∠1=∠2,∠3=∠4. 求证:△ABC≌△ABD.
A
C
B
D
1
2
3
4
(AAS)
A
B
C
D
E
F
角角边的情形包括:
两角和其中一角的对边对应相等
思考:有两个角和其中一个角的对边对应相等的两个三角形一定全等吗
例6.已知:如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B', BC=B'C'.
求证:△ABC≌△A'B'C'.
两角及其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
按角、角、边的顺序书写
能不能把“AAS”、“ASA”简述为
“两角和一边对应相等的两个三角形全等”?
A
B
C
D
E
在△ADE和△ABC中
但△ABC和△ADE不全等
结论:说明两个三角形全等时,特别注意边和角“位置上对应相等”.
例如:
其中一个角的对边对应相等
SSS
SAS
A
B
C
D
E
F
A
B
C
D
E
F
(1)
(2)
ASA
AAS
(3)
(4)
A
B
C
D
E
F
A
B
C
D
E
F
两个三角形全等
的判定条件
例7.已知∠BAC=∠ABD,∠ABC=∠DAB.
求证:AO=CO,BP=CP
∠D=∠C
∴AO=CO,BP=CP
∠D=∠C
∠OAD=∠OBC
AD= BC
∴△OAD≌△OBC(AAS)
在△OAD与△O BC中
在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC (已知)
∠A=∠A(公共角)
∴ △ABD≌△ACE (ASA)
∴AE=AD
1. 已知:AB=AC,∠B=∠C,
求证:AE=AD
A
B
D
C
E
证明:
当堂检测:
1
2
3
4
D
A
B
C
2.如图,∠1=∠2,∠3=∠4,说明:AC=AD
解:∵∠ =180 -∠3
∠ =180 -∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ 和△ 中
( )
(公共边)
( )
∴△ ≌ △ ( )
∴ (全等三角形对应边相等)
ABD
ABC
ABC
∠1=∠2
AB=AB
∠ABD=∠ABC
ASA
AC=AD
ABD
已知
已证
ABC
ABD
3.已知:如图,AD平分∠BAC,______________.
求证:BD=CD.
(请在横线上添加一个条件,使得结论成立)
思路①:根据SAS,添加
思路②:根据ASA,添加
思路③:根据AAS,添加
AB=AC
∠ ADB=∠ADC
∠B= ∠C
4.已知:如图,∠1=∠2,∠C=∠E,AC=AE.
求证:△ABC≌△ADE.
阅读下面一段文字:
泰勒斯(Thales,约公元前625~前547年)是古希腊哲学家.相传"两个角及其夹边对应相等的两个三角形全等"就是由泰勒斯首先提出的.泰勒斯利用这个判定三角形全等的依据求出了岸上一点到海中一艘船的距离.
如图,A是观察点,船P在A的正前方.过A作AP的垂线 l, 在垂线l上截取任意长AB,O 是AB 的中点.观测者从点B沿垂直于AB的BK方向走,直到点K,船P和点O在一条直线上,那么BK的距离即为船离岸的距离.请给出证明.
证明:∵AD∥BC∴∠ADB=∠CBD
∵AB∥CD∴∠ABD=∠CDB
A
B
C
D
6.已知:AB//CD,AD∥BC。
求证:△ABD≌△CDB
7.如图,已知EC=AC,∠BCE=∠ACD,∠A=∠E.求证:△ACB≌△ECD
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
