浙教版八年级上册第一章章末复习(1) 课件(共17张PPT)
文档属性
| 名称 | 浙教版八年级上册第一章章末复习(1) 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 19:00:14 | ||
图片预览



文档简介
(共17张PPT)
添加辅助线,构造全等三角形
第一章 三角形的初步知识 章末复习(1)
浙教版八年级上册
定义:(1)能够_________的两个图形称为全等图形.
(2)能够________的两个三角形叫做全等三角形.
性质:全等三角形的对应边_________,对应角_________.
重合
重合
相等
相等
判定:1、两边及其 对应相等的两个三角形全等。 简称“ ”
2、两角和它们的 对应相等的两个三角形全 等。简称“ ”
3、两角和其中一角的 对应相等的两个三角形全等。简称“ ”
4、三边 的两个三角形全等。简称“ ”
对应相等
SSS
夹角
SAS
夹边
ASA
对边
AAS
SSS
(边边边) SAS
(边角边) ASA
(角边角) AAS
(角角边)
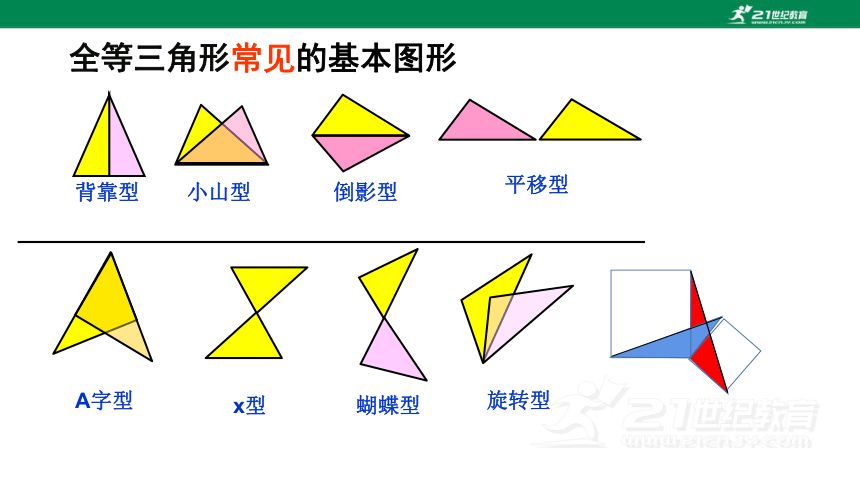
全等三角形常见的基本图形
背靠型
小山型
倒影型
平移型
旋转型
x型
A字型
蝴蝶型
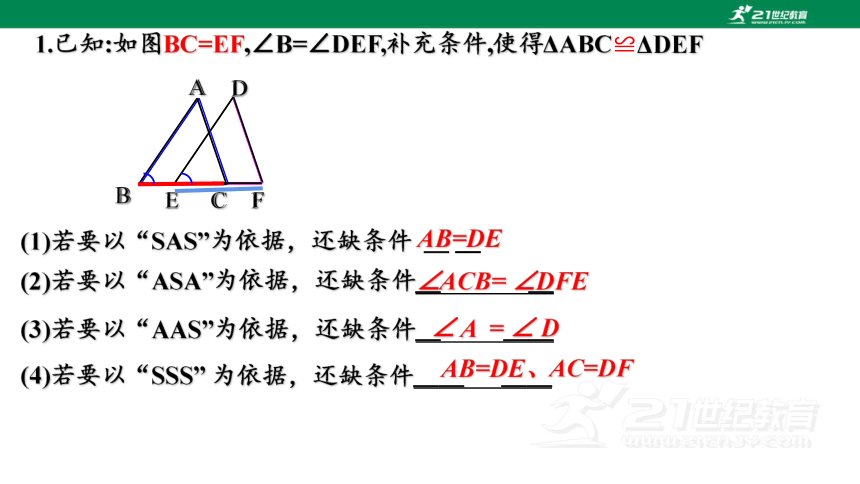
1.已知:如图BC=EF,∠B=∠DEF,补充条件,使得ΔABC≌ΔDEF
∠ACB= ∠DFE
AB=DE
AB=DE、AC=DF
∠ A = ∠ D
(1)若要以“SAS”为依据,还缺条件 _ _
(2)若要以“ASA”为依据,还缺条件_ _
(4)若要以“SSS” 为依据,还缺条件__ __
(3)若要以“AAS”为依据,还缺条件_ __
A
B
C
D
E
F
D
E
F
A
B
C
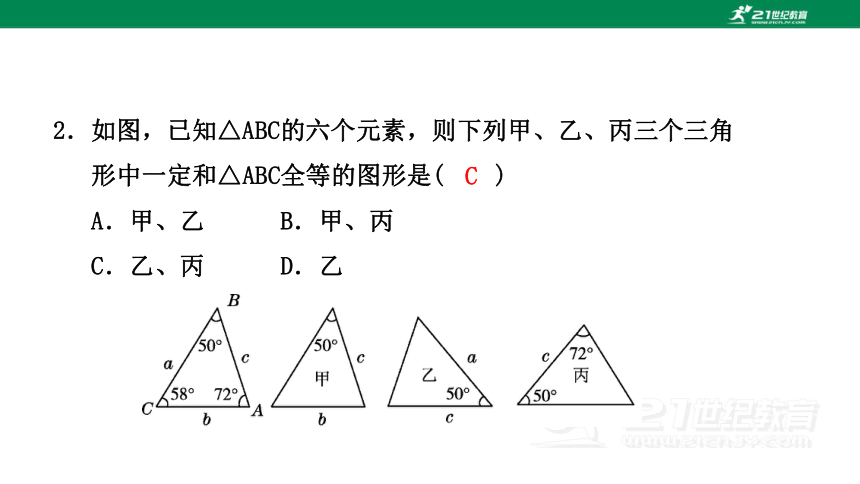
2.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙
C.乙、丙 D.乙
C
3.如图,在Rt△ABC中,∠C=90°,AC=12 cm,BC=6 cm,PQ=AB,
P,Q两点分别在线段AC和AC的垂线AX上移动,
则当AP= 时,△ABC和△APQ全等.
6 cm或12 cm
② △ABC≌△PQA
① △ABC≌△QPA
AP=AC=12 cm
AP=BC=6 cm
(P)
·
Q
·
A
C
B
O
D
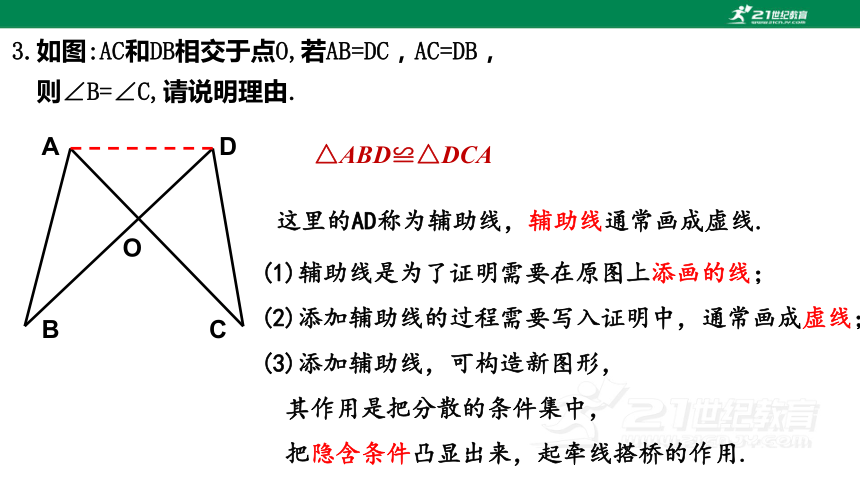
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,
则∠B=∠C,请说明理由.
(1)辅助线是为了证明需要在原图上添画的线;
(2)添加辅助线的过程需要写入证明中,通常画成虚线;
(3)添加辅助线,可构造新图形,
其作用是把分散的条件集中,
把隐含条件凸显出来,起牵线搭桥的作用.
这里的AD称为辅助线,辅助线通常画成虚线.
△ABD≌△DCA
A
C
B
O
D
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,
则∠B=∠C,请说明理由.
△ABC≌△ DCB(SSS).
∠DBC=∠ACB
∠ABC=∠DCB
∠ABC-∠DBC=∠DCB-∠ACB
∠ABD=∠ACD
A
C
B
O
D
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,
则∠B=∠C,请说明理由.
△ABC≌△ DCB(SSS).
∠A=∠D
∠ABD+∠A=∠ACD+∠D
∠ABD=∠ACD
4.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.
求证:∠2=∠1+∠C.
证明:延长AD交BC于点F,∵BE平分∠ABC,∴∠ABE=∠CBE.
∵BD⊥AD,∴∠ADB=∠BDF=90°.
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:延长AD至点E,使DE=AD,连结BE.
∵D为BC的中点,∴CD=BD.
又∵AD=ED,∠ADC=∠EDB,∴△ADC≌△EDB.
∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作BE//AC交AD的延长线于点E
∠ACD=∠EBD,∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作∠ACD=∠EBD交AD的延长线于点E,
∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.
∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
6. 已知:如图,AC∥BD,AE、BE分别平分∠CAB和∠DBA,CD过点E.
求证:AB=AC+BD.
方法一:截长法
如图,在AB上截取AF=AC,连接EF.
然后证明△AEC≌ △AEF, △BED≌△BEF.
E
C
A
B
D
F
“截长法”,即在长线段上取一段,使之等于其中一条短线段,然后证明剩下的线段等于另一条短线段.
E
C
A
B
D
F
方法二:补短法
延长BE,与AC的延长线相交于点F.然后证明△AEF≌ △AEB,△BED ≌△FEC .
已知:如图,AC∥BD,AE、BE分别平分∠CAB和∠DBA,CD过点E.
求证:AB=AC+BD.
(2)“补短法”,即延长短线段,使延长部分等于另一条短线段,再证明延长后的线段等于长线段
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
添加辅助线,构造全等三角形
第一章 三角形的初步知识 章末复习(1)
浙教版八年级上册
定义:(1)能够_________的两个图形称为全等图形.
(2)能够________的两个三角形叫做全等三角形.
性质:全等三角形的对应边_________,对应角_________.
重合
重合
相等
相等
判定:1、两边及其 对应相等的两个三角形全等。 简称“ ”
2、两角和它们的 对应相等的两个三角形全 等。简称“ ”
3、两角和其中一角的 对应相等的两个三角形全等。简称“ ”
4、三边 的两个三角形全等。简称“ ”
对应相等
SSS
夹角
SAS
夹边
ASA
对边
AAS
SSS
(边边边) SAS
(边角边) ASA
(角边角) AAS
(角角边)
全等三角形常见的基本图形
背靠型
小山型
倒影型
平移型
旋转型
x型
A字型
蝴蝶型
1.已知:如图BC=EF,∠B=∠DEF,补充条件,使得ΔABC≌ΔDEF
∠ACB= ∠DFE
AB=DE
AB=DE、AC=DF
∠ A = ∠ D
(1)若要以“SAS”为依据,还缺条件 _ _
(2)若要以“ASA”为依据,还缺条件_ _
(4)若要以“SSS” 为依据,还缺条件__ __
(3)若要以“AAS”为依据,还缺条件_ __
A
B
C
D
E
F
D
E
F
A
B
C
2.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙
C.乙、丙 D.乙
C
3.如图,在Rt△ABC中,∠C=90°,AC=12 cm,BC=6 cm,PQ=AB,
P,Q两点分别在线段AC和AC的垂线AX上移动,
则当AP= 时,△ABC和△APQ全等.
6 cm或12 cm
② △ABC≌△PQA
① △ABC≌△QPA
AP=AC=12 cm
AP=BC=6 cm
(P)
·
Q
·
A
C
B
O
D
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,
则∠B=∠C,请说明理由.
(1)辅助线是为了证明需要在原图上添画的线;
(2)添加辅助线的过程需要写入证明中,通常画成虚线;
(3)添加辅助线,可构造新图形,
其作用是把分散的条件集中,
把隐含条件凸显出来,起牵线搭桥的作用.
这里的AD称为辅助线,辅助线通常画成虚线.
△ABD≌△DCA
A
C
B
O
D
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,
则∠B=∠C,请说明理由.
△ABC≌△ DCB(SSS).
∠DBC=∠ACB
∠ABC=∠DCB
∠ABC-∠DBC=∠DCB-∠ACB
∠ABD=∠ACD
A
C
B
O
D
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,
则∠B=∠C,请说明理由.
△ABC≌△ DCB(SSS).
∠A=∠D
∠ABD+∠A=∠ACD+∠D
∠ABD=∠ACD
4.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.
求证:∠2=∠1+∠C.
证明:延长AD交BC于点F,∵BE平分∠ABC,∴∠ABE=∠CBE.
∵BD⊥AD,∴∠ADB=∠BDF=90°.
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:延长AD至点E,使DE=AD,连结BE.
∵D为BC的中点,∴CD=BD.
又∵AD=ED,∠ADC=∠EDB,∴△ADC≌△EDB.
∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作BE//AC交AD的延长线于点E
∠ACD=∠EBD,∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
5.如图,在△ABC中,D为BC的中点.
求证:AB+AC >2AD;
证明:过点B作∠ACD=∠EBD交AD的延长线于点E,
∠ADC=∠EDB,∵D为BC的中点,∴CD=BD.
∴△ADC≌△EDB.∴AC=EB.
∵AB+BE>AE,∴AB+AC>2AD.
E
·
6. 已知:如图,AC∥BD,AE、BE分别平分∠CAB和∠DBA,CD过点E.
求证:AB=AC+BD.
方法一:截长法
如图,在AB上截取AF=AC,连接EF.
然后证明△AEC≌ △AEF, △BED≌△BEF.
E
C
A
B
D
F
“截长法”,即在长线段上取一段,使之等于其中一条短线段,然后证明剩下的线段等于另一条短线段.
E
C
A
B
D
F
方法二:补短法
延长BE,与AC的延长线相交于点F.然后证明△AEF≌ △AEB,△BED ≌△FEC .
已知:如图,AC∥BD,AE、BE分别平分∠CAB和∠DBA,CD过点E.
求证:AB=AC+BD.
(2)“补短法”,即延长短线段,使延长部分等于另一条短线段,再证明延长后的线段等于长线段
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
