浙教版八年级上册第一章章末复习（2）

(共18张PPT)
第一章 三角形的初步知识 章末复习（2）
宜未雨而绸缪，勿临渴而掘井
浙教版八年级上册
由______________的三条线段首尾顺次相接所组成的图形叫做三角形．
不在同一条直线上
三角形任何两边的和_____第三边，任何两边的差____第三边．
大于
小于
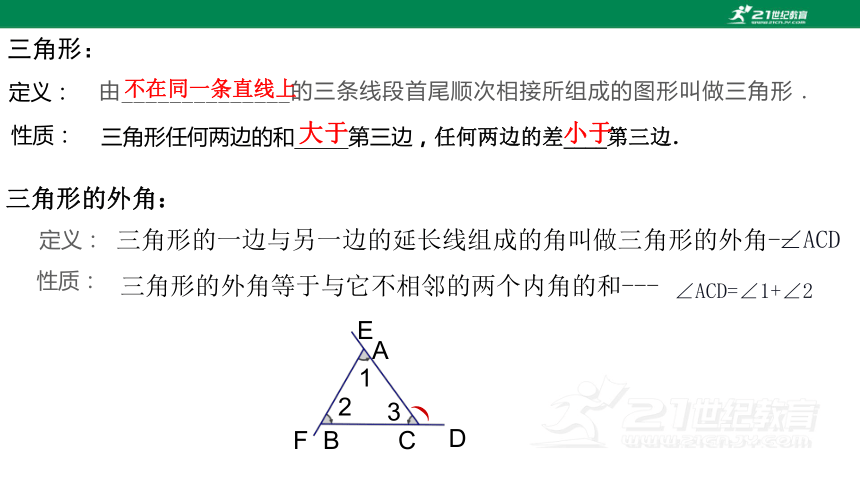
三角形的外角：
定义：
三角形的一边与另一边的延长线组成的角叫做三角形的外角--
∠ACD
性质：
三角形的外角等于与它不相邻的两个内角的和---
∠ACD=∠1+∠2
A
B
C
D
F
E
1
2
3
三角形：
定义：
性质：
(
连结三角形的一个顶点与该顶点的对边____的线段，叫做三角形的中线．
中点
三角形的中线
定义：
性质：
三角形的中线等分该三角形的面积
A
B
C
D


.
在三角形中，一个内角的___________与它的对边相交，
这个角的顶点与交点之间的线段叫做三角形的角平分线．
角平分线
三角形的角平分线：
定义：
性质：
∵ AP平分∠BAC
且PB⊥AB，PC⊥AC
∴CP=PB
角平分线上的点到角两边的距离相等.
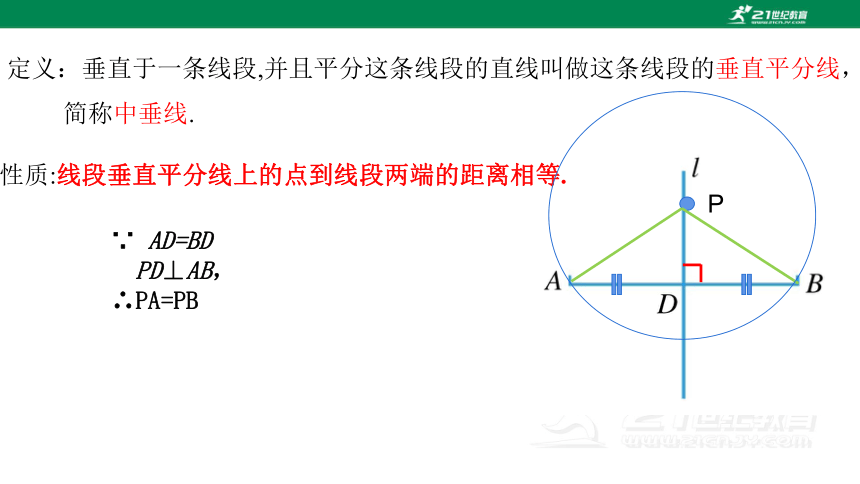
定义：垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线，
简称中垂线.
性质:线段垂直平分线上的点到线段两端的距离相等.
P
∵ AD=BD
PD⊥AB，
∴PA=PB
证明：在△ABO中，∠A+∠B+∠AOB=180°
在△COD中，∠C+∠D+∠COD=180°
∵∠AOB=∠COD
∴∠A+∠B=∠C+∠D
=1800
定义：已知AD，BC相交于O，图形像“8”字，故曰“8”字模型.
性质：8字型相对两角之和相等:∠A+∠B=∠C+∠D
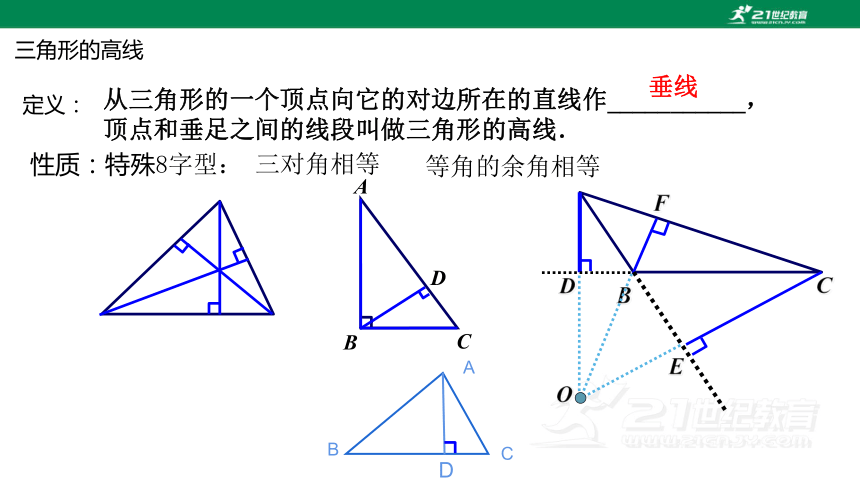
三角形的高线
定义：
性质：特殊8字型：
从三角形的一个顶点向它的对边所在的直线作___________，顶点和垂足之间的线段叫做三角形的高线．
垂线
B
C
D
F
O
E
A
B
C
D
A
B
C
D
三对角相等
等角的余角相等
SSS
SAS
A
B
C
D
E
F
A
B
C
D
E
F
（1）
（2）
ASA
AAS
（3）
（4）
A
B
C
D
E
F
A
B
C
D
E
F
两个三角形全等
的判定条件
只改变图形的位置，而不改变图形的形状和大小的变换。
全等变换：
1.轴对称型全等
D
A
C
B
2.平移型全等
3.旋转型全等
A
B
C
D
E
A
B
C
D
E
B
A
C
D
E
准备就绪：一切已经安排妥当，等待下一步
宜未雨而绸chou缪mou，勿临渴而掘井
凡事都要预先做好准备，像没到下雨的时候，
要先把房子修补完善，不要“临时抱佛脚”，
像到了口渴的时候，才来掘井。

不是全等三角形的对应边
转化为全等三角形的对应边
2.如图，△ABC，△CDE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点E在AB上．求证：△CDA≌△CEB.
证明：∵△ABC，△CDE均为等腰直角三角形，∴BC＝AC，CE＝CD.
∵∠ACB＝∠DCE＝90°，
∴∠ACB－∠ACE＝∠DCE－∠ACE，
即∠ECB＝∠DCA.

3．如图，点D在BC上，DE与AC相交于点F，若∠1＝∠2＝∠3，BC＝DE.求证：△ABC≌△ADE.
证明：∵∠1＝∠2，
∴∠1＋∠DAC＝∠2＋∠DAC，
即∠BAC＝∠DAE.
∵∠3+∠C＝∠2+∠E，∠3＝∠2，
∴∠C＝∠E.

证明:∵AD、BE是△ABC的两条高，
∴∠ADC= ∠BDH=90°
∴∠DAC+∠C = 90°
∠EBC+∠C = 90°，
∴∠DAC=∠EBC．

4
5．如图， BD⊥AC于点D, CE⊥AB于点E, AD＝AE. 求证：BE＝CD.
证明：∵ BD⊥AC, CE⊥AB，
∴∠ADB＝∠AEC＝90°.

6.如图，已知∠E＝∠F＝90°，∠1＝∠2，
AC＝AB.求证：ΔAEM≌ΔAFN.
证: ∵∠1＝∠2
∴∠1＋∠BAC＝∠2＋∠BAC
即∠EAB＝∠FAC
在ΔAEB和ΔAFC中
∴ΔAEB≌ΔAFC(AAS)
∴AE=AF
在ΔAEM和ΔAFN中
∴ΔAEM≌ΔAFN(ASA)
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin