浙教版八年级下 第4章 平行四边形 单元测试(含答案)
文档属性
| 名称 | 浙教版八年级下 第4章 平行四边形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 99.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 15:22:18 | ||
图片预览

文档简介
浙教版八年级下 第4章 平行四边形 单元测试
一.选择题(共12小题)
1.如图是四款新能源汽车的标志,其中是中心对称图形的是( )
A. B. C. D.
2.如果一个多边形的每个内角都相等,且内角和为2340°,那么这个多边形的一个外角的度数为( )
A.24° B.30° C.36° D.60°
3.在四边形ABCD中,两组对边分别相等.若∠B=70°,则∠C的度数为( )
A.100° B.110° C.120° D.130°
4.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A.4cm B.6cm C.8cm D.12cm
5.如图,在平行四边形ABCD中,AC,BD相交于点O,若AC=8,则线段AO的长为( )
A.3 B.4 C.5 D.16
6.如图,以A,B,C,D为顶点的四边形是平行四边形,则点D的位置可以在( )
A.① B.② C.③ D.④
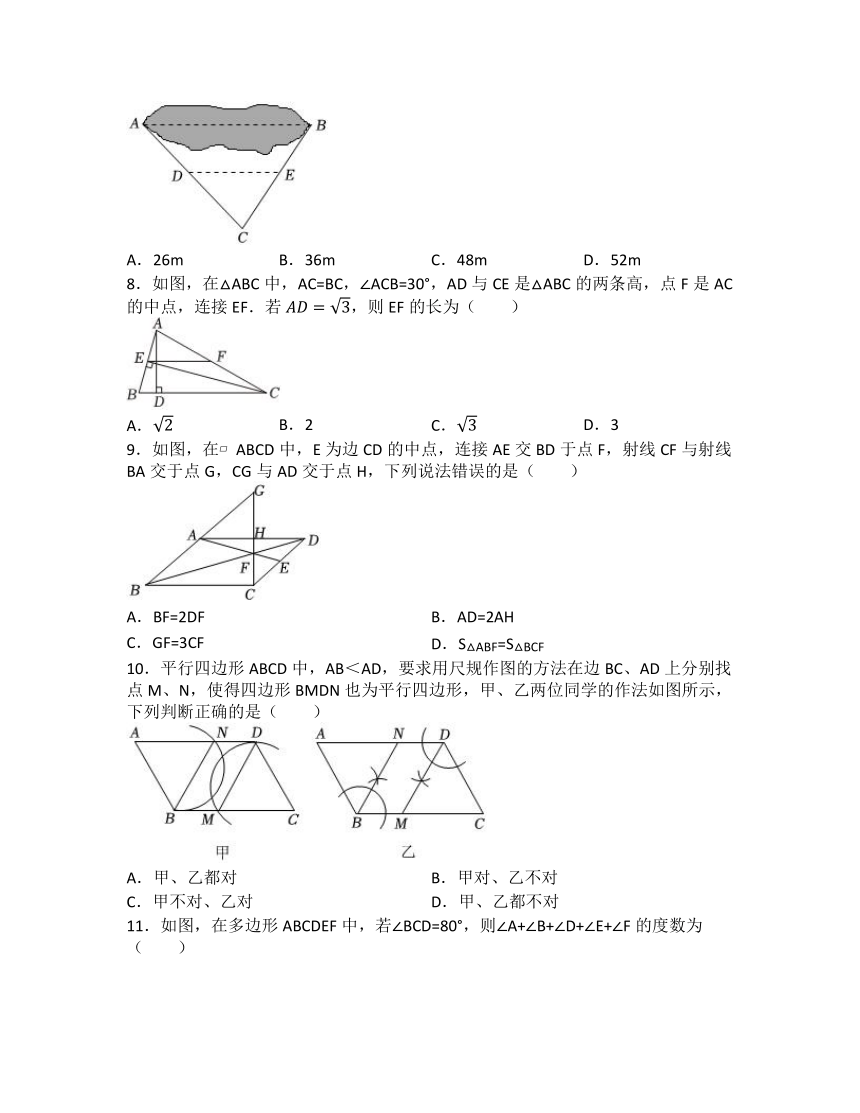
7.为美化环境,毕节市政府计划在池塘上搭建小桥,如图,地面上A,B两处被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点D,E.测得DE=26m,则A,B两处的距离为( )
A.26m B.36m C.48m D.52m
8.如图,在△ABC中,AC=BC,∠ACB=30°,AD与CE是△ABC的两条高,点F是AC的中点,连接EF.若,则EF的长为( )
A. B.2 C. D.3
9.如图,在 ABCD中,E为边CD的中点,连接AE交BD于点F,射线CF与射线BA交于点G,CG与AD交于点H,下列说法错误的是( )
A.BF=2DF B.AD=2AH
C.GF=3CF D.S△ABF=S△BCF
10.平行四边形ABCD中,AB<AD,要求用尺规作图的方法在边BC、AD上分别找点M、N,使得四边形BMDN也为平行四边形,甲、乙两位同学的作法如图所示,下列判断正确的是( )
A.甲、乙都对 B.甲对、乙不对
C.甲不对、乙对 D.甲、乙都不对
11.如图,在多边形ABCDEF中,若∠BCD=80°,则∠A+∠B+∠D+∠E+∠F的度数为( )
A.250° B.330° C.440° D.540°
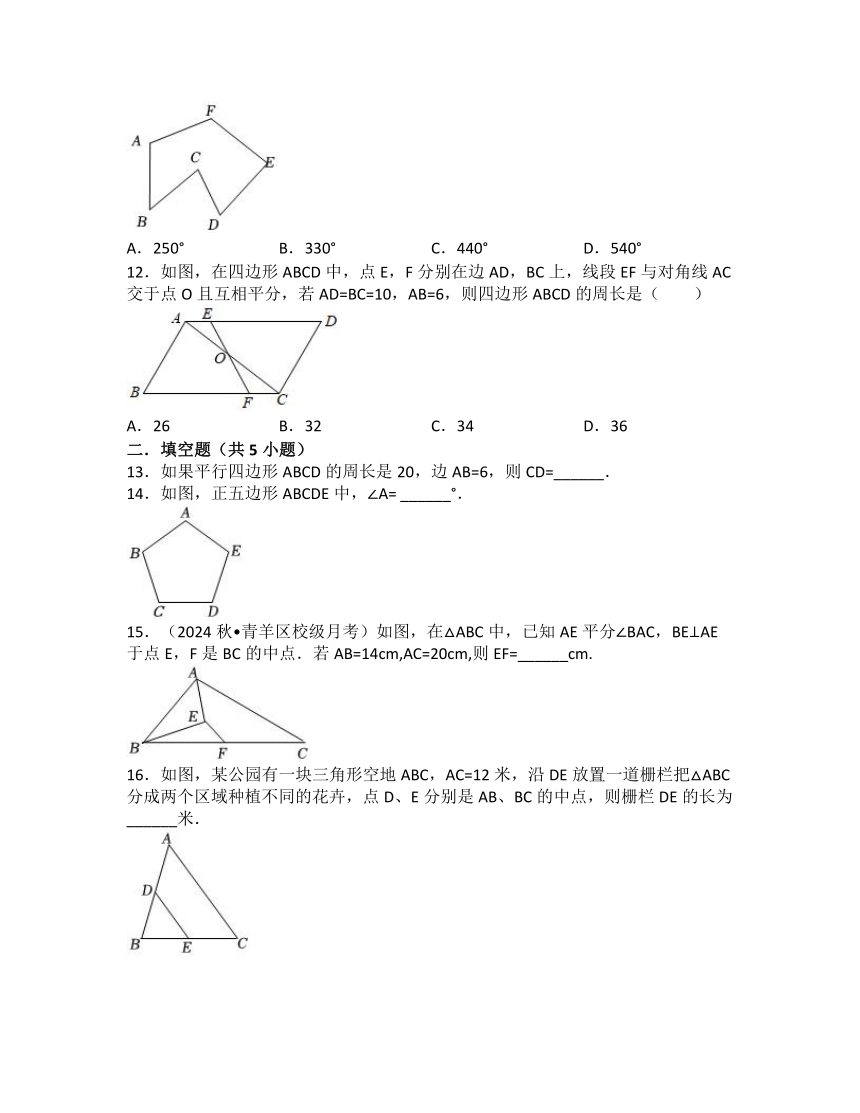
12.如图,在四边形ABCD中,点E,F分别在边AD,BC上,线段EF与对角线AC交于点O且互相平分,若AD=BC=10,AB=6,则四边形ABCD的周长是( )
A.26 B.32 C.34 D.36
二.填空题(共5小题)
13.如果平行四边形ABCD的周长是20,边AB=6,则CD=______.
14.如图,正五边形ABCDE中,∠A= ______°.
15.(2024秋 青羊区校级月考)如图,在△ABC中,已知AE平分∠BAC,BE⊥AE于点E,F是BC的中点.若AB=14cm,AC=20cm,则EF=______cm.
16.如图,某公园有一块三角形空地ABC,AC=12米,沿DE放置一道栅栏把△ABC分成两个区域种植不同的花卉,点D、E分别是AB、BC的中点,则栅栏DE的长为 ______米.
17.如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有 ______(填序号).
三.解答题(共5小题)
18.(1)计算:÷2-×.
(2)如图, ABCD中,E为BC边的中点,连接AE并与DC的延长线交于点F,求证:DC=CF.
19.(1)计算:.
(2)如图所示,延长△ABC的中线BD至点E,使DE=BD,连接AE、CE.求证:四边形ABCE是平行四边形.
20.如图,已知四边形ABCD中,AD∥CB,BD平分∠ABC,∠A:∠DBA=4:1.
(1)求∠A的度数;
(2)如果△BDC是直角三角形,直接写出∠C的度数.
21.如图,平行四边形ABCD中,AO平分∠BAC,OB=OC,延长DC与AO交于点P,连接BP.
(1)求证:CD=CP;
(2)判断四边形ABPC的形状,并证明你的结论.
22.如图,在 ABCD中,AB=2,AD=3,过点A作AE⊥BC,垂足为E.连接AC、BD,交于点O,连接OE,延长EO交AD于点F.
(1)若BE=1,求AC的长;
(2)求证:AO=EF.
浙教版八年级下 第4章 平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、A 3、B 4、C 5、B 6、B 7、D 8、C 9、C 10、A 11、C 12、B
二.填空题(共5小题)
13、6; 14、108; 15、3; 16、6; 17、①②③④;
三.解答题(共5小题)
18、(1)解:原式=2÷2-
=
=0;
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠CFE;
∵E为BC中点,
∴EB=EC,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF,
∴DC=CF.
19、(1)解:
=5-4+1
=2;
(2)证明:∵BD是△ABC的中线,
∴AD=CD,
又∵∠ADB=∠CDE,DE=BE,
∴△ADB≌△CDE(SAS),
∴AB=CE,∠ABD=∠CED,
∴AB∥CE,
∴四边形ABCE是平行四边形.
20、解:(1)AD∥CB,
∵BD平分∠ABC,
∴∠ABC=2∠ABD.
∵∠A:∠DBA=4:1,
∵∠ABC+∠A=180°,
∴∠A=120°.
(2)∵AD∥CB,∠A=120°,
∴∠DBC=∠ABD=30°.
由三角形的内角和,得
∠C=180°-∠DBC-∠BDC=180°-30°-90°=60°.
21、(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB∥DP,
∴∠BAP=∠CPA,
在△ABO和△PCO中,
,
∴△ABO≌△PCO(AAS),
∴CP=AB,
又∵AB=CD,
∴CD=CP;
(2)解:四边形ABPC是菱形,理由如下:
∵AB=CP,AB∥CP,
∴四边形ABPC是平行四边形,
∵AO平分∠BAC,
∴∠BAO=∠CAO,
∴∠CPO=∠CAO,
∴AC=CP,
∴四边形ABPC是菱形.
22、(1)解:∵AE⊥BC,BE=1,AB=2,
∴AE2=AB2-BE2=3,
∵四边形ABCD是平行四边形,
∴BC=AD=3,
∴CE=BC-BE=2,
∴AC===;
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAF=∠OCE,
在△OAF和△OCE中,
,
∴△OAF≌△OCE(ASA),
∴OE=OF,
∵AD∥BC,AE⊥BC,
∴AE⊥AD,
∴AO=EF.
一.选择题(共12小题)
1.如图是四款新能源汽车的标志,其中是中心对称图形的是( )
A. B. C. D.
2.如果一个多边形的每个内角都相等,且内角和为2340°,那么这个多边形的一个外角的度数为( )
A.24° B.30° C.36° D.60°
3.在四边形ABCD中,两组对边分别相等.若∠B=70°,则∠C的度数为( )
A.100° B.110° C.120° D.130°
4.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A.4cm B.6cm C.8cm D.12cm
5.如图,在平行四边形ABCD中,AC,BD相交于点O,若AC=8,则线段AO的长为( )
A.3 B.4 C.5 D.16
6.如图,以A,B,C,D为顶点的四边形是平行四边形,则点D的位置可以在( )
A.① B.② C.③ D.④
7.为美化环境,毕节市政府计划在池塘上搭建小桥,如图,地面上A,B两处被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点D,E.测得DE=26m,则A,B两处的距离为( )
A.26m B.36m C.48m D.52m
8.如图,在△ABC中,AC=BC,∠ACB=30°,AD与CE是△ABC的两条高,点F是AC的中点,连接EF.若,则EF的长为( )
A. B.2 C. D.3
9.如图,在 ABCD中,E为边CD的中点,连接AE交BD于点F,射线CF与射线BA交于点G,CG与AD交于点H,下列说法错误的是( )
A.BF=2DF B.AD=2AH
C.GF=3CF D.S△ABF=S△BCF
10.平行四边形ABCD中,AB<AD,要求用尺规作图的方法在边BC、AD上分别找点M、N,使得四边形BMDN也为平行四边形,甲、乙两位同学的作法如图所示,下列判断正确的是( )
A.甲、乙都对 B.甲对、乙不对
C.甲不对、乙对 D.甲、乙都不对
11.如图,在多边形ABCDEF中,若∠BCD=80°,则∠A+∠B+∠D+∠E+∠F的度数为( )
A.250° B.330° C.440° D.540°
12.如图,在四边形ABCD中,点E,F分别在边AD,BC上,线段EF与对角线AC交于点O且互相平分,若AD=BC=10,AB=6,则四边形ABCD的周长是( )
A.26 B.32 C.34 D.36
二.填空题(共5小题)
13.如果平行四边形ABCD的周长是20,边AB=6,则CD=______.
14.如图,正五边形ABCDE中,∠A= ______°.
15.(2024秋 青羊区校级月考)如图,在△ABC中,已知AE平分∠BAC,BE⊥AE于点E,F是BC的中点.若AB=14cm,AC=20cm,则EF=______cm.
16.如图,某公园有一块三角形空地ABC,AC=12米,沿DE放置一道栅栏把△ABC分成两个区域种植不同的花卉,点D、E分别是AB、BC的中点,则栅栏DE的长为 ______米.
17.如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有 ______(填序号).
三.解答题(共5小题)
18.(1)计算:÷2-×.
(2)如图, ABCD中,E为BC边的中点,连接AE并与DC的延长线交于点F,求证:DC=CF.
19.(1)计算:.
(2)如图所示,延长△ABC的中线BD至点E,使DE=BD,连接AE、CE.求证:四边形ABCE是平行四边形.
20.如图,已知四边形ABCD中,AD∥CB,BD平分∠ABC,∠A:∠DBA=4:1.
(1)求∠A的度数;
(2)如果△BDC是直角三角形,直接写出∠C的度数.
21.如图,平行四边形ABCD中,AO平分∠BAC,OB=OC,延长DC与AO交于点P,连接BP.
(1)求证:CD=CP;
(2)判断四边形ABPC的形状,并证明你的结论.
22.如图,在 ABCD中,AB=2,AD=3,过点A作AE⊥BC,垂足为E.连接AC、BD,交于点O,连接OE,延长EO交AD于点F.
(1)若BE=1,求AC的长;
(2)求证:AO=EF.
浙教版八年级下 第4章 平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、A 3、B 4、C 5、B 6、B 7、D 8、C 9、C 10、A 11、C 12、B
二.填空题(共5小题)
13、6; 14、108; 15、3; 16、6; 17、①②③④;
三.解答题(共5小题)
18、(1)解:原式=2÷2-
=
=0;
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠CFE;
∵E为BC中点,
∴EB=EC,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF,
∴DC=CF.
19、(1)解:
=5-4+1
=2;
(2)证明:∵BD是△ABC的中线,
∴AD=CD,
又∵∠ADB=∠CDE,DE=BE,
∴△ADB≌△CDE(SAS),
∴AB=CE,∠ABD=∠CED,
∴AB∥CE,
∴四边形ABCE是平行四边形.
20、解:(1)AD∥CB,
∵BD平分∠ABC,
∴∠ABC=2∠ABD.
∵∠A:∠DBA=4:1,
∵∠ABC+∠A=180°,
∴∠A=120°.
(2)∵AD∥CB,∠A=120°,
∴∠DBC=∠ABD=30°.
由三角形的内角和,得
∠C=180°-∠DBC-∠BDC=180°-30°-90°=60°.
21、(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB∥DP,
∴∠BAP=∠CPA,
在△ABO和△PCO中,
,
∴△ABO≌△PCO(AAS),
∴CP=AB,
又∵AB=CD,
∴CD=CP;
(2)解:四边形ABPC是菱形,理由如下:
∵AB=CP,AB∥CP,
∴四边形ABPC是平行四边形,
∵AO平分∠BAC,
∴∠BAO=∠CAO,
∴∠CPO=∠CAO,
∴AC=CP,
∴四边形ABPC是菱形.
22、(1)解:∵AE⊥BC,BE=1,AB=2,
∴AE2=AB2-BE2=3,
∵四边形ABCD是平行四边形,
∴BC=AD=3,
∴CE=BC-BE=2,
∴AC===;
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAF=∠OCE,
在△OAF和△OCE中,
,
∴△OAF≌△OCE(ASA),
∴OE=OF,
∵AD∥BC,AE⊥BC,
∴AE⊥AD,
∴AO=EF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
