5.1 认识方程 课件(共25张PPT) 浙教版七年级数学上册
文档属性
| 名称 | 5.1 认识方程 课件(共25张PPT) 浙教版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 20:45:40 | ||
图片预览








文档简介
(共25张PPT)
5.1.认识方程
学习目标
1.通过观察,归纳一元一次方程的概念
2.理解方程的解的概念;
3.通过对多种实际问题中的数量关系的分析,
感受方程是刻画现实生活中数量关系的有效模型。
2x+5=21
10x + 15(45-x)= 475
x(x+25)= 5850
请大家观察这4个表示量相等的式子,它们有什么共同的特点?
由不同的代数式来表示相等的量。
知识点
1
方程(概念)
方程
知识点
1
方程(概念)
方程
提问:方程有什么特点?
提问:列方程解决实际问题的关键是什么?
(1)方程中一定含有未知数
(2)方程一定是等式
等量关系
小试牛刀
下面哪些式子是方程?哪些不是?
√
√
×
√
×
×
请观察3个方程有什么共同点?
这3个方程与下面的2个方程有什么不同点?
只含有1个未知数
未知数次数不是1
代数式不是整式
知识点
2
一元一次方程(概念)
只含有1个未知数
未知数次数是1
且方程中的代数式都是整式
把这样的方程叫作一元一次方程
在方程中
其中一元一次方程有
①④
一元二次方程
二元一次方程
一元二次方程
分式方程
解:
-1
-1
÷2
÷2
知识点
3
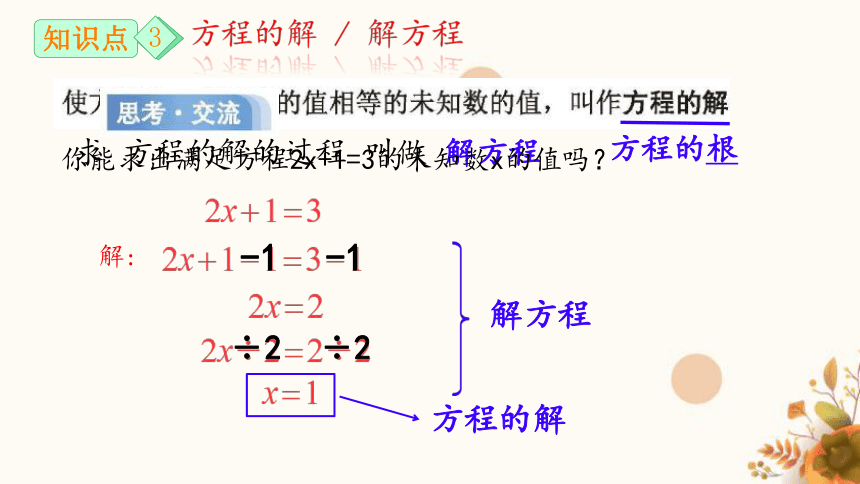
方程的解 / 解方程
方程的根
求 方程的解的过程 叫做 解方程
方程的解
解方程
你能求出满足方程2x+1=3的未知数x的值吗?
知识点
4
检验方程的解
课本P137 随堂练习
解:
将x=2代入方程左、右两边
左边 = 3×2+(10-2)
= 6+8
= 14
右边 = 20
左边≠右边
∴x=2不是方程3x+(10-x)=20的解
将方程的解代入方程左右两边
左边=右边,则是方程的解
左边≠右边,则不是方程的解
学习单 题4
这些式子都是用不同的代数式表示相等的量。
含有未知数的表示量相等的等式称为方程
归纳总结
诚信做人 踏实做事
归纳总结
在一个方程中,只含有一个未知数,且方程中的代数式都是整式,未知数的次数都是1,这样的方程叫做一元一次方程。
-5x + 675 = 475
探究1:在班级秋游活动中,全体学生和老师共购买了 45 张门票,学生票每张 10 元,成人票每张 15 元,总票款为 475 元。你知道学生和老师的人数分别是多少吗?购买学生票和成人票的票款分别是多少?
合作探究
(1)这个问题涉及哪些量?它们之间有怎样的等量关系?
(2)如果设学生人数为 x,那么总票款可以用含 x 的代数式表示为 。
10x + 15(45 - x)
老师人数 + 学生人数 = 总人数
(3)你能得到怎样的表示量相等的式子?
学生票款 + 成人票款 = 总票款
10x + 15(45 - x) = 475
+ = 总票款
↓
学生票价×学生人数
↓
成人票价×老师人数
问题1:某长方形操场的面积是 5850 m2,长比宽多 25 m。
(1)这个情境涉及哪些量?它们之间有怎样的等量关系?
(2)如果设这个操场的宽为 x m,那么操场的面积可以用含 x 的代数式表为 。
(3)你能得到怎样的表示量相等的式子?
自主思考
长×宽 = 长方形面积
长 - 宽 = 25
x(x + 25)
x(x + 25) = 5850
问题2:甲、乙两地相距 22 km,张叔叔从甲地出发
到乙地,每小时比原计划多走 1 km,因此提前 12 min 到达乙地。
(1)这个情境涉及哪些量?它们之间有怎样的等量关系?
(2)如果设张叔叔原计划每小时走 x km,那么他比原计划提前的时间可以用含 x 的代数式表示为 。
(3)你能得到怎样的表示量相等的式子?
速度×时间 = 路程
计划时间 - 实际时间 = 12
实际速度 - 计划速度 = 1 km/h
解:设小彬今年x岁,依题意,得:
2x-5=21.
问题3
问题2:甲、乙两地相距22km,张叔叔从甲地出发到乙地,每时比原计划多行走1km,因此提前12min到达乙地。张叔叔原计划每时行走多少千米?
解:设张叔叔原计划每时行走x km,依题意,得:
问题4:根据第七次全国人口普查统计数据,截至2020年11月1日0时,全国每10万人中具有大学文化程度的人数为8930人,与2010年第六次全国人口普查相比增长了147.30 %。2010年第六次人口普查时每10万人中约有多少人具有大学文化程度?
解:设2010年第六次人口普查时每10万人中约有x人具有大学文化程度,可以得到方程:
一般步骤:①找等量关系;②设未知数,用字母表示;③列出方程.
1.以上问题中,根据题意列出方程的关键是什么?一般步骤是什么?
2.下面哪些方程是你熟悉的?它们有哪些共同的特点?
思考·交流
你能求出满足该方程的未知数x的值吗?
如何做到的,请在小组内进行交流。
总结
使方程左、右两边的值相等的未知数的值,叫作方程的解。求方程的解的过程称为解方程。
练一练
一、根据题意,设出未知数,列出方程:
(1)在公元前1600年左右遗留下来的一卷古埃及纸草书中,记载着一些数学问题。其中一个问题翻译过来是:"啊哈,它的全部,它的 ,其和等于19。"你能求出问题中的"它"吗?
(2)某球队参加足球联赛,规定每队胜一场得3分,平一场得1分,负一场得0分。该球队已比赛了10场,并保持不败,一共得了22分。该球队已胜了多少场?平了多少场?
二.x=2是下列方程的解吗?
(1)3x+(10- x )=20;
(2)2x +6=7x.
练一练
总结
总结
知识点
1
方程(概念)
知识点
2
一元一次方程(概念)
只含有1个未知数
未知数次数是1
且方程中的代数式都是整式
把这样的方程叫作一元一次方程
在方程中
方程
总结
总结
知识点
3
方程的解 / 解方程
方程的根
求 方程的解的过程 叫做 解方程
知识点
4
检验方程的解
将方程的解代入方程左右两边
左边=右边,则是方程的解
左边≠右边,则不是方程的解
5.1.认识方程
学习目标
1.通过观察,归纳一元一次方程的概念
2.理解方程的解的概念;
3.通过对多种实际问题中的数量关系的分析,
感受方程是刻画现实生活中数量关系的有效模型。
2x+5=21
10x + 15(45-x)= 475
x(x+25)= 5850
请大家观察这4个表示量相等的式子,它们有什么共同的特点?
由不同的代数式来表示相等的量。
知识点
1
方程(概念)
方程
知识点
1
方程(概念)
方程
提问:方程有什么特点?
提问:列方程解决实际问题的关键是什么?
(1)方程中一定含有未知数
(2)方程一定是等式
等量关系
小试牛刀
下面哪些式子是方程?哪些不是?
√
√
×
√
×
×
请观察3个方程有什么共同点?
这3个方程与下面的2个方程有什么不同点?
只含有1个未知数
未知数次数不是1
代数式不是整式
知识点
2
一元一次方程(概念)
只含有1个未知数
未知数次数是1
且方程中的代数式都是整式
把这样的方程叫作一元一次方程
在方程中
其中一元一次方程有
①④
一元二次方程
二元一次方程
一元二次方程
分式方程
解:
-1
-1
÷2
÷2
知识点
3
方程的解 / 解方程
方程的根
求 方程的解的过程 叫做 解方程
方程的解
解方程
你能求出满足方程2x+1=3的未知数x的值吗?
知识点
4
检验方程的解
课本P137 随堂练习
解:
将x=2代入方程左、右两边
左边 = 3×2+(10-2)
= 6+8
= 14
右边 = 20
左边≠右边
∴x=2不是方程3x+(10-x)=20的解
将方程的解代入方程左右两边
左边=右边,则是方程的解
左边≠右边,则不是方程的解
学习单 题4
这些式子都是用不同的代数式表示相等的量。
含有未知数的表示量相等的等式称为方程
归纳总结
诚信做人 踏实做事
归纳总结
在一个方程中,只含有一个未知数,且方程中的代数式都是整式,未知数的次数都是1,这样的方程叫做一元一次方程。
-5x + 675 = 475
探究1:在班级秋游活动中,全体学生和老师共购买了 45 张门票,学生票每张 10 元,成人票每张 15 元,总票款为 475 元。你知道学生和老师的人数分别是多少吗?购买学生票和成人票的票款分别是多少?
合作探究
(1)这个问题涉及哪些量?它们之间有怎样的等量关系?
(2)如果设学生人数为 x,那么总票款可以用含 x 的代数式表示为 。
10x + 15(45 - x)
老师人数 + 学生人数 = 总人数
(3)你能得到怎样的表示量相等的式子?
学生票款 + 成人票款 = 总票款
10x + 15(45 - x) = 475
+ = 总票款
↓
学生票价×学生人数
↓
成人票价×老师人数
问题1:某长方形操场的面积是 5850 m2,长比宽多 25 m。
(1)这个情境涉及哪些量?它们之间有怎样的等量关系?
(2)如果设这个操场的宽为 x m,那么操场的面积可以用含 x 的代数式表为 。
(3)你能得到怎样的表示量相等的式子?
自主思考
长×宽 = 长方形面积
长 - 宽 = 25
x(x + 25)
x(x + 25) = 5850
问题2:甲、乙两地相距 22 km,张叔叔从甲地出发
到乙地,每小时比原计划多走 1 km,因此提前 12 min 到达乙地。
(1)这个情境涉及哪些量?它们之间有怎样的等量关系?
(2)如果设张叔叔原计划每小时走 x km,那么他比原计划提前的时间可以用含 x 的代数式表示为 。
(3)你能得到怎样的表示量相等的式子?
速度×时间 = 路程
计划时间 - 实际时间 = 12
实际速度 - 计划速度 = 1 km/h
解:设小彬今年x岁,依题意,得:
2x-5=21.
问题3
问题2:甲、乙两地相距22km,张叔叔从甲地出发到乙地,每时比原计划多行走1km,因此提前12min到达乙地。张叔叔原计划每时行走多少千米?
解:设张叔叔原计划每时行走x km,依题意,得:
问题4:根据第七次全国人口普查统计数据,截至2020年11月1日0时,全国每10万人中具有大学文化程度的人数为8930人,与2010年第六次全国人口普查相比增长了147.30 %。2010年第六次人口普查时每10万人中约有多少人具有大学文化程度?
解:设2010年第六次人口普查时每10万人中约有x人具有大学文化程度,可以得到方程:
一般步骤:①找等量关系;②设未知数,用字母表示;③列出方程.
1.以上问题中,根据题意列出方程的关键是什么?一般步骤是什么?
2.下面哪些方程是你熟悉的?它们有哪些共同的特点?
思考·交流
你能求出满足该方程的未知数x的值吗?
如何做到的,请在小组内进行交流。
总结
使方程左、右两边的值相等的未知数的值,叫作方程的解。求方程的解的过程称为解方程。
练一练
一、根据题意,设出未知数,列出方程:
(1)在公元前1600年左右遗留下来的一卷古埃及纸草书中,记载着一些数学问题。其中一个问题翻译过来是:"啊哈,它的全部,它的 ,其和等于19。"你能求出问题中的"它"吗?
(2)某球队参加足球联赛,规定每队胜一场得3分,平一场得1分,负一场得0分。该球队已比赛了10场,并保持不败,一共得了22分。该球队已胜了多少场?平了多少场?
二.x=2是下列方程的解吗?
(1)3x+(10- x )=20;
(2)2x +6=7x.
练一练
总结
总结
知识点
1
方程(概念)
知识点
2
一元一次方程(概念)
只含有1个未知数
未知数次数是1
且方程中的代数式都是整式
把这样的方程叫作一元一次方程
在方程中
方程
总结
总结
知识点
3
方程的解 / 解方程
方程的根
求 方程的解的过程 叫做 解方程
知识点
4
检验方程的解
将方程的解代入方程左右两边
左边=右边,则是方程的解
左边≠右边,则不是方程的解
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
