数学:第三章圆的基本性质复习课件(浙教版九年级上)2
文档属性
| 名称 | 数学:第三章圆的基本性质复习课件(浙教版九年级上)2 |  | |
| 格式 | rar | ||
| 文件大小 | 478.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-30 14:33:00 | ||
图片预览






文档简介
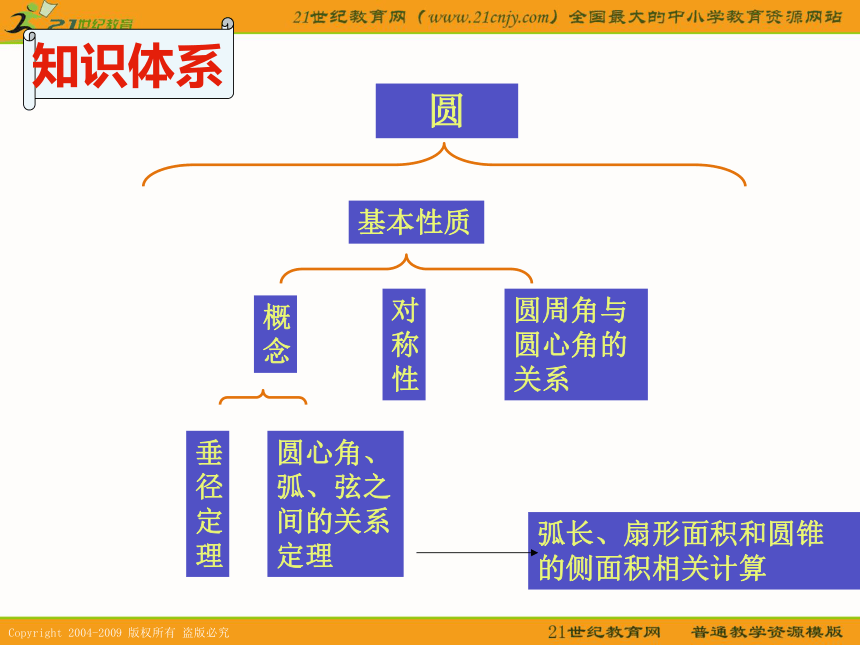
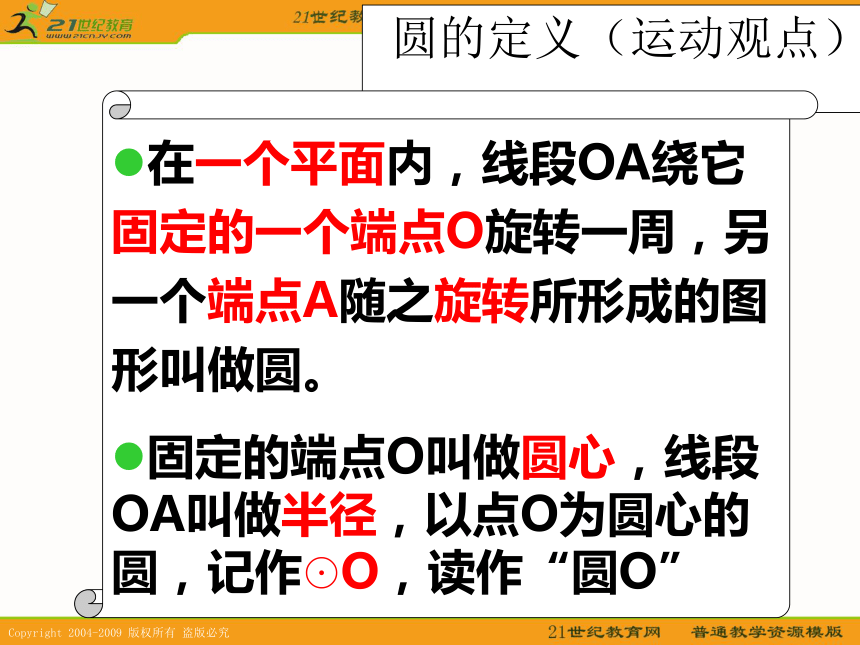
课件27张PPT。第三章:圆的基本性质知识体系圆基本性质概念对称性垂径定理圆心角、弧、弦之间的关系定理圆周角与圆心角的关系弧长、扇形面积和圆锥的侧面积相关计算圆的定义(运动观点)在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆。
固定的端点O叫做圆心,线段OA叫做半径,以点O为圆心的圆,记作☉O,读作“圆O”圆的定义辨析篮球是圆吗?
圆必须在一个平面内
以3cm为半径画圆,能画多少个?
以点O为圆心画圆,能画多少个?
由此,你发现半径和圆心分别有什么作用?
半径确定圆的大小;圆心确定圆的位置
圆是“圆周”还是“圆面”?
圆是一条封闭曲线
圆周上的点与圆心有什么关系?点与圆的位置关系圆是到定点(圆心)的距离等于定长(半径)的点的集合。
圆的内部是到圆心的距离小于半径的点的集合。
圆的外部是到圆心的距离大于半径的点的集合。
由此,你发现点与圆的位置关系是由什么来决定的呢?如果圆的半径为r,
点到圆心的距离为d,则:
点在圆上? d=r
点在圆内? d 点在圆外? d>r圆的有关性质过三点的圆思考:确定一条直线的条件是什么?
类比联想:是否也存在由几个点确定一个圆呢?
讨论:经过一个点,能作出多少个圆?
经过两个点,如何作圆,能作多少个?
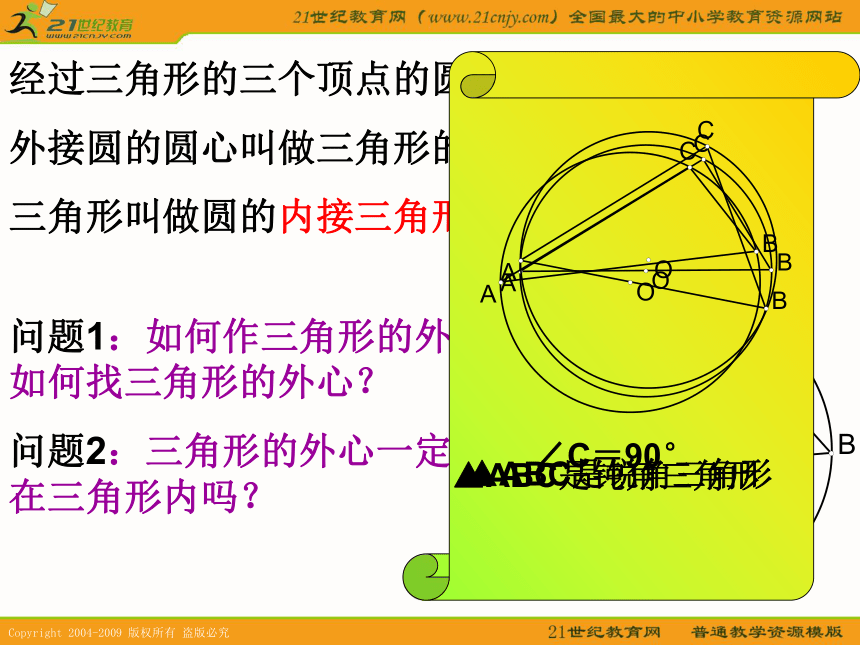
经过三个点,如何作圆,能作多少个?经过三角形的三个顶点的圆叫做三角形的外接圆,
外接圆的圆心叫做三角形的外心,
三角形叫做圆的内接三角形。问题1:如何作三角形的外接圆?如何找三角形的外心?
问题2:三角形的外心一定 在三角形内吗?∠C=90°▲ABC是锐角三角形▲ABC是钝角三角形垂直于弦的直径及其推论从特殊到一般想一想:将一个圆沿着任一条直径对折,两侧半圆会有什么关系?
性质:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴。观察右图,有什么等量关系?垂直于弦的直径AO=BO=CO=DO,弧AD=弧BC,弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BC=弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BD,弧AC=弧BC, AE=BE 。垂径定理垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。判断下列图形,能否使用垂径定理?注意:定理中的两个条件(直径,垂直于弦)缺一不可!定理辨析练习若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?变式1:AC、BD有什么关系?变式2:AC=BD依然成立吗?变式3:EA=____, EC=_____。OA=OBOC=OD变式练习如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。辅助线关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。推论1如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?推论2弧AE=弧BF圆的两条平行弦所夹的弧相等。圆的性质圆是轴对称图形,每一条直径所在的直线都是对称轴。
圆是以圆心为对称中心的中心对称图形。
圆还具有旋转不变性,即圆绕圆心旋转任意一个角度α,都能与原来的图形重合。圆心角:顶点在圆心的角。
(如:∠AOB)弦心距:从圆心到弦的距离。
(如:OC)相关定义圆心角所对的弧相等, 圆心角所对的弦相等, 圆心角所对弦的弦心距相等。推论 在同圆或等圆中,
如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有
一组量相等,那么它们所对应
的其余各组量都分别相等。在同圆或等圆中
(前提)圆心角相等
(条件)
定理推论圆心角:如∠BOA圆内角:如∠BCA圆周角:如∠BDA圆外角:如∠BFA角的顶点在圆心角的顶点在圆周上
是否顶点在圆周上的角就是圆周角呢?动起来!圆周角:顶点在圆上,并且两边都和圆相交的角。
圆心角: 顶点在圆心的角.看清要点推论定理:一条弧所对的圆周角等于它所对的圆心角的一半。
也可以理解为:一条弧所对的圆心角是它所对的圆周角的二倍;圆周角的度数等于它所对的弧的度数的一半。弧相等,圆周角是否相等?反过来呢?
什么时候圆周角是直角?反过来呢?
直角三角形斜边中线有什么性质?反过来呢?
推论1 同弧或等弧所对的圆周角相等; 同圆或等圆中,相等的圆周角所对的弧相等。思考:
1、“同圆或等圆”的条件能否去掉?
2、判断正误:在同圆或等圆中,如果两个
圆心角、两条弧、两条弦、两条弦心距、两个
圆周角中有一组量相等,那么它们所对应的
其余各组量也相等。推论2 半圆(或直径)所对的圆周角是90°;90°的圆周角所对的弦是直径。推论3 如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形。什么时候圆周角是直角?反过来呢?
直角三角形斜边中线有什么性质?反过来呢?
弧长与扇形的面积: 如果用字母S表示扇形的面积,n表示所求面积的扇形的圆心角的度数,r表示圆的半径,那么扇形的面积计算公式是 (1)(2)圆锥的侧面积和全面积:S侧=S全=小结和同步作业:P89-93:
目标与评定
固定的端点O叫做圆心,线段OA叫做半径,以点O为圆心的圆,记作☉O,读作“圆O”圆的定义辨析篮球是圆吗?
圆必须在一个平面内
以3cm为半径画圆,能画多少个?
以点O为圆心画圆,能画多少个?
由此,你发现半径和圆心分别有什么作用?
半径确定圆的大小;圆心确定圆的位置
圆是“圆周”还是“圆面”?
圆是一条封闭曲线
圆周上的点与圆心有什么关系?点与圆的位置关系圆是到定点(圆心)的距离等于定长(半径)的点的集合。
圆的内部是到圆心的距离小于半径的点的集合。
圆的外部是到圆心的距离大于半径的点的集合。
由此,你发现点与圆的位置关系是由什么来决定的呢?如果圆的半径为r,
点到圆心的距离为d,则:
点在圆上? d=r
点在圆内? d
类比联想:是否也存在由几个点确定一个圆呢?
讨论:经过一个点,能作出多少个圆?
经过两个点,如何作圆,能作多少个?
经过三个点,如何作圆,能作多少个?经过三角形的三个顶点的圆叫做三角形的外接圆,
外接圆的圆心叫做三角形的外心,
三角形叫做圆的内接三角形。问题1:如何作三角形的外接圆?如何找三角形的外心?
问题2:三角形的外心一定 在三角形内吗?∠C=90°▲ABC是锐角三角形▲ABC是钝角三角形垂直于弦的直径及其推论从特殊到一般想一想:将一个圆沿着任一条直径对折,两侧半圆会有什么关系?
性质:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴。观察右图,有什么等量关系?垂直于弦的直径AO=BO=CO=DO,弧AD=弧BC,弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BC=弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BD,弧AC=弧BC, AE=BE 。垂径定理垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。判断下列图形,能否使用垂径定理?注意:定理中的两个条件(直径,垂直于弦)缺一不可!定理辨析练习若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?变式1:AC、BD有什么关系?变式2:AC=BD依然成立吗?变式3:EA=____, EC=_____。OA=OBOC=OD变式练习如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。辅助线关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。推论1如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?推论2弧AE=弧BF圆的两条平行弦所夹的弧相等。圆的性质圆是轴对称图形,每一条直径所在的直线都是对称轴。
圆是以圆心为对称中心的中心对称图形。
圆还具有旋转不变性,即圆绕圆心旋转任意一个角度α,都能与原来的图形重合。圆心角:顶点在圆心的角。
(如:∠AOB)弦心距:从圆心到弦的距离。
(如:OC)相关定义圆心角所对的弧相等, 圆心角所对的弦相等, 圆心角所对弦的弦心距相等。推论 在同圆或等圆中,
如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有
一组量相等,那么它们所对应
的其余各组量都分别相等。在同圆或等圆中
(前提)圆心角相等
(条件)
定理推论圆心角:如∠BOA圆内角:如∠BCA圆周角:如∠BDA圆外角:如∠BFA角的顶点在圆心角的顶点在圆周上
是否顶点在圆周上的角就是圆周角呢?动起来!圆周角:顶点在圆上,并且两边都和圆相交的角。
圆心角: 顶点在圆心的角.看清要点推论定理:一条弧所对的圆周角等于它所对的圆心角的一半。
也可以理解为:一条弧所对的圆心角是它所对的圆周角的二倍;圆周角的度数等于它所对的弧的度数的一半。弧相等,圆周角是否相等?反过来呢?
什么时候圆周角是直角?反过来呢?
直角三角形斜边中线有什么性质?反过来呢?
推论1 同弧或等弧所对的圆周角相等; 同圆或等圆中,相等的圆周角所对的弧相等。思考:
1、“同圆或等圆”的条件能否去掉?
2、判断正误:在同圆或等圆中,如果两个
圆心角、两条弧、两条弦、两条弦心距、两个
圆周角中有一组量相等,那么它们所对应的
其余各组量也相等。推论2 半圆(或直径)所对的圆周角是90°;90°的圆周角所对的弦是直径。推论3 如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形。什么时候圆周角是直角?反过来呢?
直角三角形斜边中线有什么性质?反过来呢?
弧长与扇形的面积: 如果用字母S表示扇形的面积,n表示所求面积的扇形的圆心角的度数,r表示圆的半径,那么扇形的面积计算公式是 (1)(2)圆锥的侧面积和全面积:S侧=S全=小结和同步作业:P89-93:
目标与评定
同课章节目录
