数学:第四章相似三角形复习课件(浙教版九年级上)2
文档属性
| 名称 | 数学:第四章相似三角形复习课件(浙教版九年级上)2 |  | |
| 格式 | rar | ||
| 文件大小 | 381.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-30 14:33:00 | ||
图片预览




文档简介
课件38张PPT。相似三角形复习课1、对应角相等,对应边成比例
2、对应角平分线、对应中线、对应高线、对应周长的比都等于相似比。
3、相似三角形面积的比等于相似比的平方。1、相似三角形的性质:知识要点练习:1.地图上的1cm2面积表示实际200m2的面积,则该地图的比例尺是__________.2.两个相似三角形的面积比为m,周长比为2,则m=________.43.边长为2的正三角形被平行一边的直线分成等积的两部分,
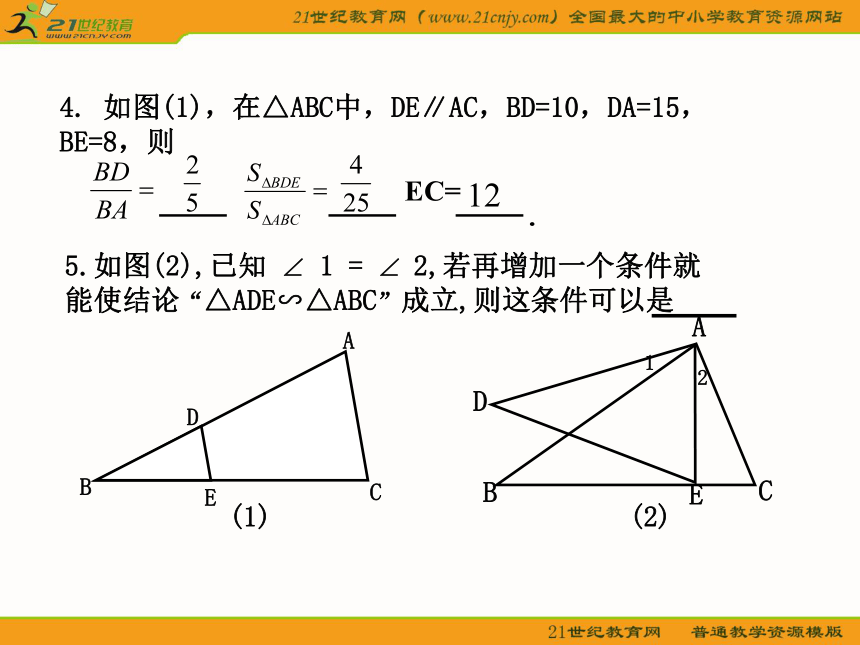
其中一部分是梯形,则这个梯形的上底长为_______.4. 如图(1),在△ABC中,DE∥AC,BD=10,DA=15,BE=8,则EC=
.BDECA5.如图(2),已知 ∠ 1 = ∠ 2,若再增加一个条件就能使结论“△ADE∽△ABC”成立,则这条件可以是(1)ADBE(2)C12
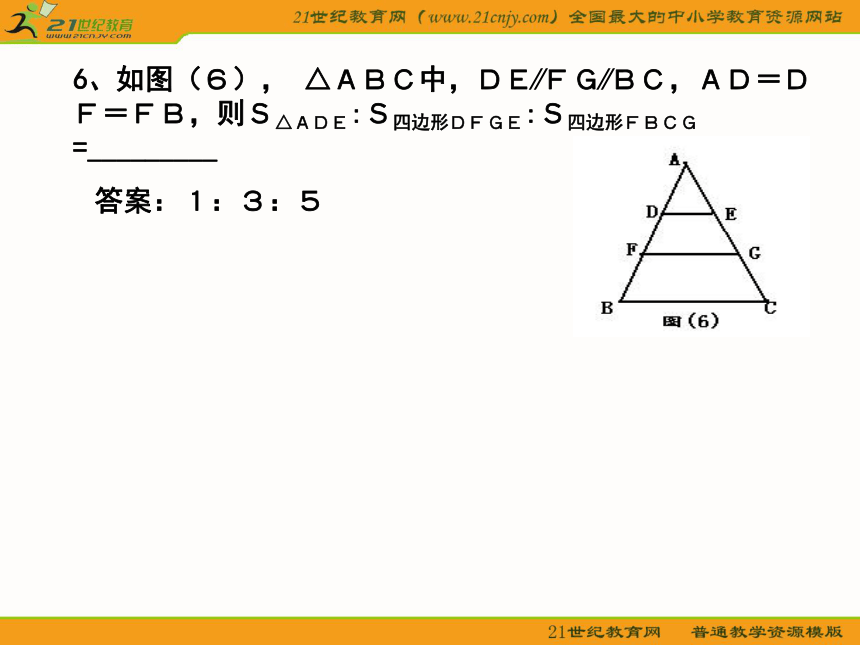
6、如图(6), △ABC中,DE??FG??BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
答案:1:3:5范例分析:易证,△ HMP∽△PDE∽△GPF,得 一.填空选择题:
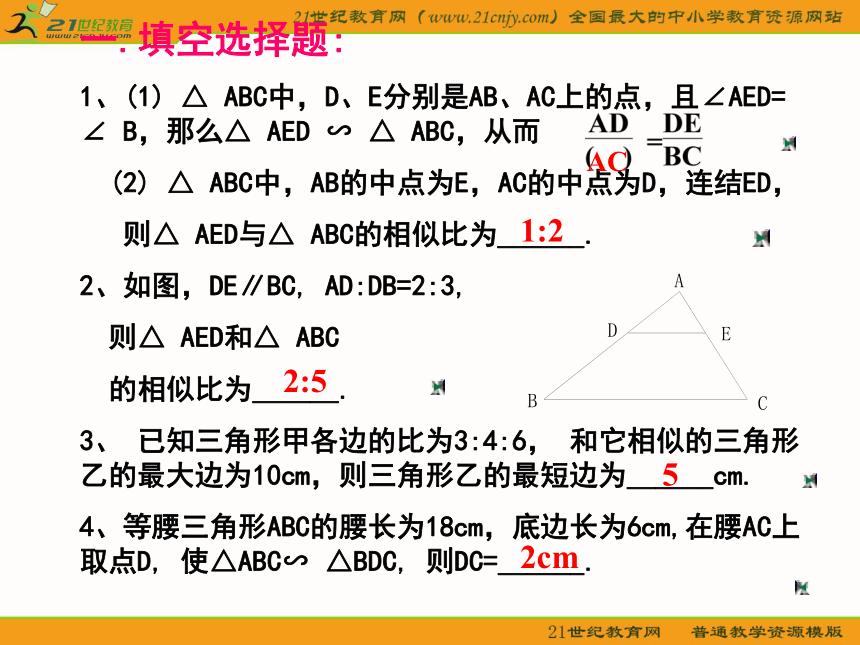
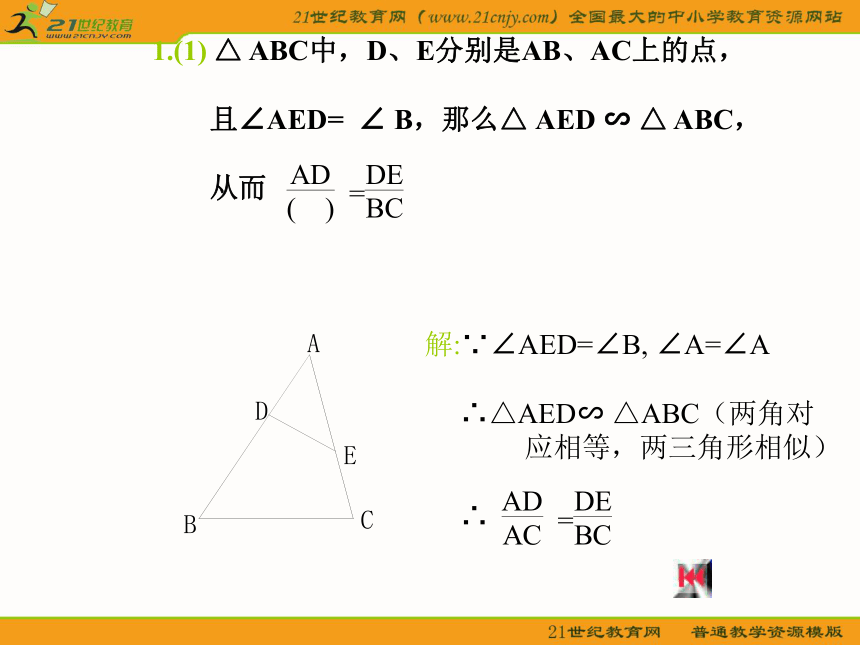
1、(1) △ ABC中,D、E分别是AB、AC上的点,且∠AED= ∠ B,那么△ AED ∽ △ ABC,从而
(2) △ ABC中,AB的中点为E,AC的中点为D,连结ED,
则△ AED与△ ABC的相似比为______.
2、如图,DE∥BC, AD:DB=2:3,
则△ AED和△ ABC
的相似比为___.
3、 已知三角形甲各边的比为3:4:6, 和它相似的三角形乙的最大边为10cm,则三角形乙的最短边为______cm.
4、等腰三角形ABC的腰长为18cm,底边长为6cm,在腰AC上取点D, 使△ABC∽ △BDC, 则DC=______.
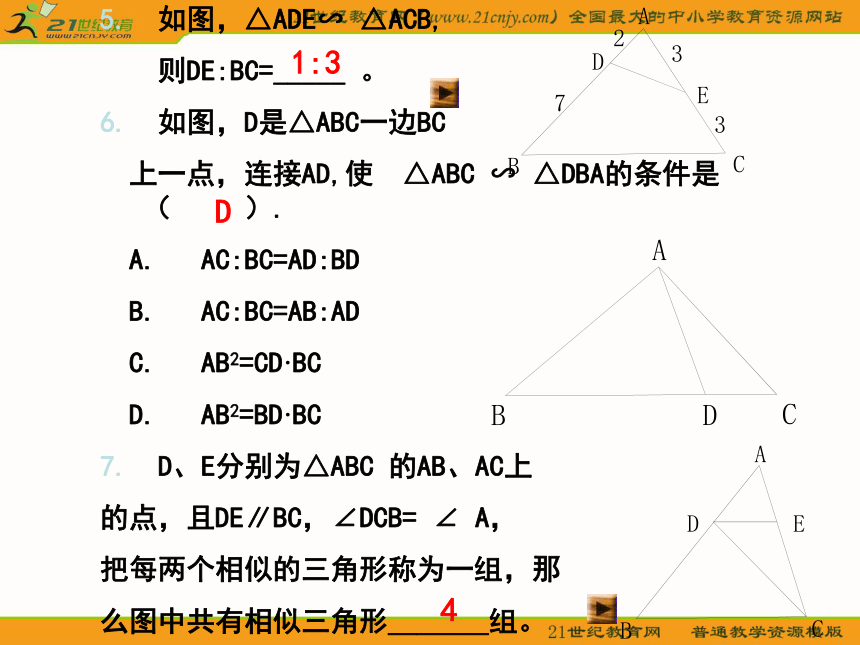
AC2:552cm1:25. 如图,△ADE∽ △ACB,
则DE:BC=_____ 。
6. 如图,D是△ABC一边BC
上一点,连接AD,使 △ABC ∽ △DBA的条件是( ).
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BC
7. D、E分别为△ABC 的AB、AC上
的点,且DE∥BC,∠DCB= ∠ A,
把每两个相似的三角形称为一组,那
么图中共有相似三角形_______组。
1:3D4二、证明题:
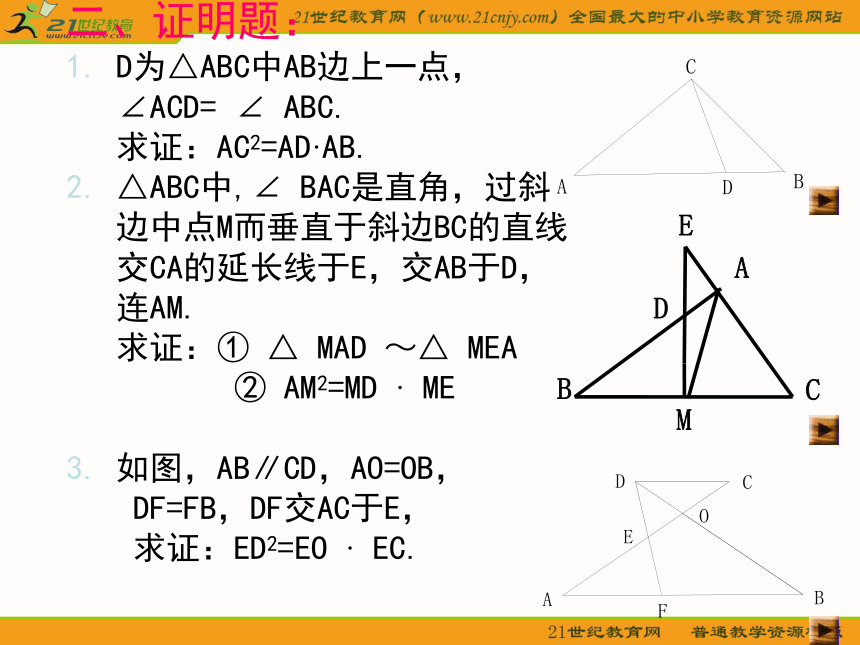
1. D为△ABC中AB边上一点,
∠ACD= ∠ ABC.
求证:AC2=AD·AB.
2. △ABC中,∠ BAC是直角,过斜
边中点M而垂直于斜边BC的直线
交CA的延长线于E,交AB于D,
连AM.
求证:① △ MAD ~△ MEA
② AM2=MD · ME
3. 如图,AB∥CD,AO=OB,
DF=FB,DF交AC于E,
求证:ED2=EO · EC.E
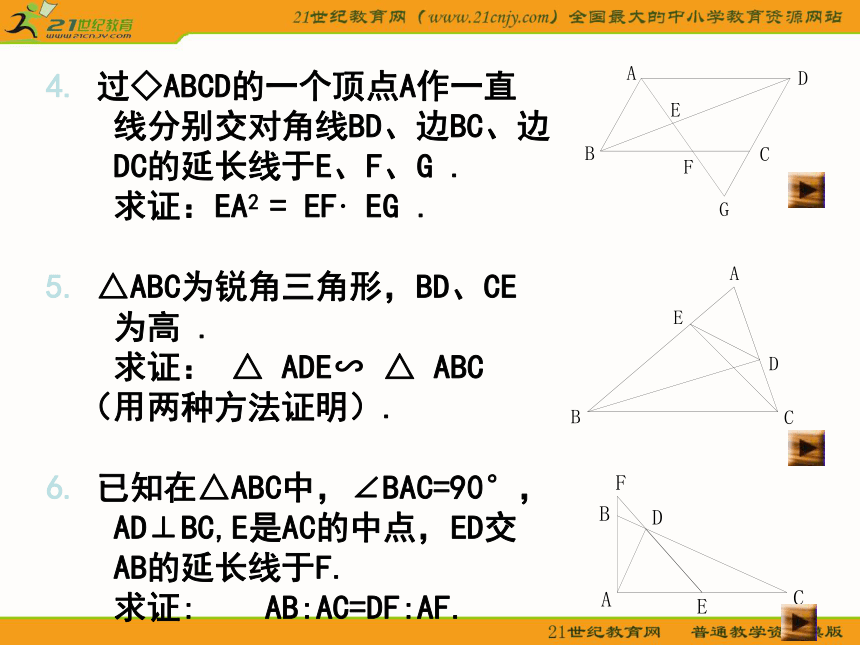
4. 过◇ABCD的一个顶点A作一直
线分别交对角线BD、边BC、边
DC的延长线于E、F、G .
求证:EA2 = EF· EG .
5. △ABC为锐角三角形,BD、CE
为高 .
求证: △ ADE∽ △ ABC
(用两种方法证明).
6. 已知在△ABC中,∠BAC=90°,
AD⊥BC,E是AC的中点,ED交
AB的延长线于F.
求证: AB:AC=DF:AF. 解:∵∠AED=∠B, ∠A=∠A
∴△AED∽ △ABC(两角对
应相等,两三角形相似)
∴
1.(1) △ ABC中,D、E分别是AB、AC上的点,
且∠AED= ∠ B,那么△ AED ∽ △ ABC,
从而
解 :∵D、E分别为AB、AC的中点
∴DE∥BC,且
∴ △ADE∽△ABC
即△ADE与△ABC的相似比为1:2
(2) △ ABC中,AB的中点为D,AC的中点为E,连结DE,
则△ ADE与△ ABC的相似比为______2. 解: ∵DE∥BC
∴△ADE∽△ABC
∵AD:DB=2:3
∴DB:AD=3:2
∴(DB+AD):AD=(2+3):3
即 AB:AD=5:2
∴AD:AB=2:5
即△ADE与△ABC的相似比为2:5 如图,DE∥BC, AD:DB=2:3, 则△ AED
和△ ABC 的相似比为___.
3.已知三角形甲各边的比为3:4:6, 和它相似的三角形乙
的最大边为10cm, 则三角形乙的最短边为______cm.解: 设三角形甲为△ABC ,三角
形乙为 △DEF,且△DEF的最大
边为DE,最短边为EF
∵ △DEF∽△ABC
∴ DE:EF=6:3
即 10:EF=6:3
∴ EF=5cm4.等腰三角形ABC的腰长为18cm,底边长为6cm,在
腰AC上取点D, 使△ABC∽ △BDC, 则DC=______.解: ∵ △ABC ∽△BDC
∴
即
∴ DC=2cm5.解: ∵ △ADE∽△ACB
且
∴如图,△ADE∽ △ACB, 则DE:BC=_____ 。7. D、E分别为△ABC 的AB、AC上的点,DE∥BC,
∠DCB= ∠ A,把每两个相似的三角形称为一组,
那么图中共有相似三角形_______组。解: ∵ DE∥BC
∴∠ADE= ∠B,
∠EDC=∠DCB=∠A
① ∵ DE∥BC
∴△ADE ∽ △ABC
② ∵ ∠A= ∠DCB, ∠ADE= ∠B
∴△ADE∽ △CBD
③ ∵ △ADE ∽ △ABC
△ADE ∽ △CBD
∴ △ABC ∽ △CBD
④ ∵ ∠DCA= ∠DCE, ∠A= ∠EDC
∴ △ADC ∽ △DEC1. D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB分析:要证明AC2=AD·AB,需
要先将乘积式改写为比例
式 ,再证明AC、
AD、AB所在的两个三角形相
似。由已知两个三角形有二个
角对应相等,所以两三角形相
似,本题可证。证明:∵ ∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·AB2. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:① △ MAD ~△ MEA ② AM2=MD · ME分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。AM是△ MAD 与△ MEA 的公共边,故是对应边MD、ME的比例中项。证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴ ∠B= ∠MAD
又 ∵ ∠B+ ∠BDM=90°
∠E+ ∠ADE= 90°
∠BDM= ∠ADE∴∠B=∠E
∴∠MAD= ∠E
又 ∵ ∠DMA= ∠AME
∴△MAD∽ △MEA② ∵ △MAD∽ △MEA
∴
即AM2=MD·ME3. 过◇ABCD的一个顶点A作一直线分别交对角线BD、边
BC、边DC的延长线于E、F、G .
求证:EA2 = EF· EG . 分析:要证明
EA2 = EF· EG ,
即 证明 成
立,而EA、EG、EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△AED∽△FEB, △AEB ∽ △GED.证明:∵ AD∥BF AB∥BC
∴△AED ∽△FEB
△AEB ∽△GED
∴
∴4. △ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC(用两种方法证明).证明一:
∵BD⊥AC,CE⊥AB
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°
∴ ∠ABD= ∠ACE
又∵ ∠A= ∠A
∴△ ABD ∽ △ ACE
∴
∵ ∠A= ∠A
∴ △ ADE ∽ △ ABC
证明二:∵ ∠BEO= ∠CDO
∠ BOE=∠COD
∴ △BOE ∽ △COD
∴
即
又∵ ∠BOC= ∠EOD
∴ △BOC ∽△EOD
∴ ∠1= ∠2
∵ ∠1+ ∠BCD=90°,
∠2+ ∠3= ∠ 90°
∴ ∠ BCD= ∠3
又∵ ∠A= ∠A
∴ △ ADE∽ △ ABC6. 已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的
中点,ED交AB的延长线于F. 求证: AB:AC=DF:AF.分析:因△ABC∽△ABD,所以
, 要证
即证 ,
需证△BDF∽△DAF.证明:∵ ∠BAC=90°
AD⊥BC
∴ ∠ABC+∠C= 90°
∠ABC+∠BAD= 90°
∴ ∠BAD= ∠C
∵ ∠ADC= 90°
E是AC的中点,
∴ED=EC
∴ ∠EDC= ∠C
∵ ∠EDC = ∠BDF
∴ ∠BDF= ∠C= ∠BAD
又∵ ∠F =∠F
∴ △BDF∽△DAF.
∴
∵ ∠BAC=90°, AD⊥BC
∴ △ABC∽△ABD
∴
∴
1.已知:如图,△ABC中,P是AB边上的一点,连结CP.满足什么条件时△ ACP∽△ABC. 解:⑴∵∠A= ∠A,∴当∠1= ∠ACB (或∠2= ∠B)时,△ ACP∽△ABC
⑵ ∵∠A= ∠A,∴当AC:AP=AB:AC时,
△ ACP∽△ABC
⑶ ∵∠A= ∠A,
当∠4+∠ACB=180°时, △ ACP∽△ABC答:当∠1= ∠ACB 或∠2= ∠B 或AC:AP=AB:AC或∠4+∠ACB=180°时,△ ACP∽△ABC.1、条件探索型二、探索题2.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似1 这类题型结论是明确的,而需要完备使结论成立的条件.解题思路是:从给定结论出发,通过逆向思考寻求使结论成立的条件. 1.将两块完全相同的等腰直角三角板摆成如图的样子,假设图形中的所有点、线都在同一平面内,则图中有相似(不包括全等)三角形吗?如有,把它们一 一写出来.C解:有相似三角形,它们是:△ADE∽ △BAE, △BAE ∽ △CDA ,△ADE∽ △CDA( △ADE∽ △BAE ∽ △CDA)2、结论探索型2.△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.EEEE 这类题型的特征是有条件而无结论,要确定这些条件下可能出现的结论.解题思路是:从所给条件出发,通过分析、比较、猜想、寻求多种解法和结论,再进行证明. 3、存在探索型 1、 如图, DE是△ABC的中位线,在射线AF上是否存在点M,使△MEC与△ADE相似,若存在,请先确定点 M,再证明这两个三角形相似,若不存在,请说明理由.证明:连结MC, ∵DE是△ABC的中位线, ∴DE∥BC,AE=EC, 又∵ME⊥AC, ∴AM=CM, ∴ ∠1= ∠2 , ∵∠B=90°, ∴ ∠4= ∠B= 90°, ∵AF ∥BC,AM ∥DE, ∴ ∠1= ∠2 , ∴ ∠3= ∠2 , ∵ ∠ADE= ∠MEC=90 ° , ∴ △ADE ∽△MEC.123M解:存在.过点E作AC的垂线,与AF交于一点,即M点(或作∠MCA= ∠AED).4例2、如图,已知:AB⊥DB于点B ,CD⊥DB于点D,AB=6,CD=4,BD=14.
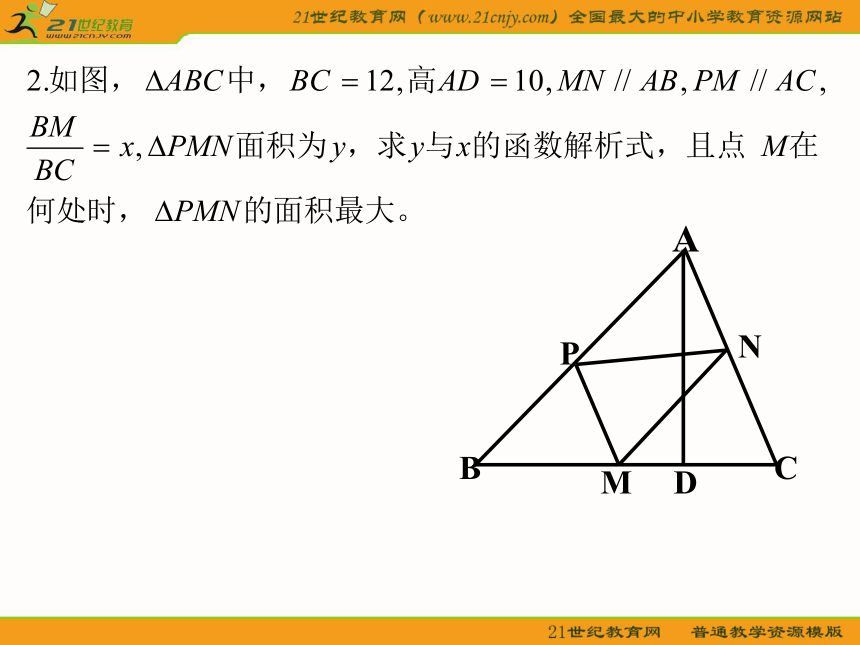
问:在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由。P(2)假设存在这样的点P,使△ABP∽△PDC,则
则有AB:PD=PB:CD设PD=x,则PB=14―x,
∴6: x =(14―x): 4∴x=2或x=12∴x=2或x=12或x=5.6时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似46x14―xDBCAp 所谓存在性问题,一般是要求确定满足某些特定要求的元素有或没有的问题.解题思路是:先假定所需探索的对象存在或结论成立,以此为依据进行计算或推理,若由此推出矛盾,则假定是错误的,从而给出否定的结论,否则给出肯定的证明. ②探究:在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。Q练习:∽ABCDFE三、位似 两个多边形不仅相似,而且对应顶点的连线相交于一点,这样的相似叫做位似,点O叫做位似中心.利用位似的方法,可以把一个多边形放大或缩小
2、对应角平分线、对应中线、对应高线、对应周长的比都等于相似比。
3、相似三角形面积的比等于相似比的平方。1、相似三角形的性质:知识要点练习:1.地图上的1cm2面积表示实际200m2的面积,则该地图的比例尺是__________.2.两个相似三角形的面积比为m,周长比为2,则m=________.43.边长为2的正三角形被平行一边的直线分成等积的两部分,
其中一部分是梯形,则这个梯形的上底长为_______.4. 如图(1),在△ABC中,DE∥AC,BD=10,DA=15,BE=8,则EC=
.BDECA5.如图(2),已知 ∠ 1 = ∠ 2,若再增加一个条件就能使结论“△ADE∽△ABC”成立,则这条件可以是(1)ADBE(2)C12
6、如图(6), △ABC中,DE??FG??BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
答案:1:3:5范例分析:易证,△ HMP∽△PDE∽△GPF,得 一.填空选择题:
1、(1) △ ABC中,D、E分别是AB、AC上的点,且∠AED= ∠ B,那么△ AED ∽ △ ABC,从而
(2) △ ABC中,AB的中点为E,AC的中点为D,连结ED,
则△ AED与△ ABC的相似比为______.
2、如图,DE∥BC, AD:DB=2:3,
则△ AED和△ ABC
的相似比为___.
3、 已知三角形甲各边的比为3:4:6, 和它相似的三角形乙的最大边为10cm,则三角形乙的最短边为______cm.
4、等腰三角形ABC的腰长为18cm,底边长为6cm,在腰AC上取点D, 使△ABC∽ △BDC, 则DC=______.
AC2:552cm1:25. 如图,△ADE∽ △ACB,
则DE:BC=_____ 。
6. 如图,D是△ABC一边BC
上一点,连接AD,使 △ABC ∽ △DBA的条件是( ).
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BC
7. D、E分别为△ABC 的AB、AC上
的点,且DE∥BC,∠DCB= ∠ A,
把每两个相似的三角形称为一组,那
么图中共有相似三角形_______组。
1:3D4二、证明题:
1. D为△ABC中AB边上一点,
∠ACD= ∠ ABC.
求证:AC2=AD·AB.
2. △ABC中,∠ BAC是直角,过斜
边中点M而垂直于斜边BC的直线
交CA的延长线于E,交AB于D,
连AM.
求证:① △ MAD ~△ MEA
② AM2=MD · ME
3. 如图,AB∥CD,AO=OB,
DF=FB,DF交AC于E,
求证:ED2=EO · EC.E
4. 过◇ABCD的一个顶点A作一直
线分别交对角线BD、边BC、边
DC的延长线于E、F、G .
求证:EA2 = EF· EG .
5. △ABC为锐角三角形,BD、CE
为高 .
求证: △ ADE∽ △ ABC
(用两种方法证明).
6. 已知在△ABC中,∠BAC=90°,
AD⊥BC,E是AC的中点,ED交
AB的延长线于F.
求证: AB:AC=DF:AF. 解:∵∠AED=∠B, ∠A=∠A
∴△AED∽ △ABC(两角对
应相等,两三角形相似)
∴
1.(1) △ ABC中,D、E分别是AB、AC上的点,
且∠AED= ∠ B,那么△ AED ∽ △ ABC,
从而
解 :∵D、E分别为AB、AC的中点
∴DE∥BC,且
∴ △ADE∽△ABC
即△ADE与△ABC的相似比为1:2
(2) △ ABC中,AB的中点为D,AC的中点为E,连结DE,
则△ ADE与△ ABC的相似比为______2. 解: ∵DE∥BC
∴△ADE∽△ABC
∵AD:DB=2:3
∴DB:AD=3:2
∴(DB+AD):AD=(2+3):3
即 AB:AD=5:2
∴AD:AB=2:5
即△ADE与△ABC的相似比为2:5 如图,DE∥BC, AD:DB=2:3, 则△ AED
和△ ABC 的相似比为___.
3.已知三角形甲各边的比为3:4:6, 和它相似的三角形乙
的最大边为10cm, 则三角形乙的最短边为______cm.解: 设三角形甲为△ABC ,三角
形乙为 △DEF,且△DEF的最大
边为DE,最短边为EF
∵ △DEF∽△ABC
∴ DE:EF=6:3
即 10:EF=6:3
∴ EF=5cm4.等腰三角形ABC的腰长为18cm,底边长为6cm,在
腰AC上取点D, 使△ABC∽ △BDC, 则DC=______.解: ∵ △ABC ∽△BDC
∴
即
∴ DC=2cm5.解: ∵ △ADE∽△ACB
且
∴如图,△ADE∽ △ACB, 则DE:BC=_____ 。7. D、E分别为△ABC 的AB、AC上的点,DE∥BC,
∠DCB= ∠ A,把每两个相似的三角形称为一组,
那么图中共有相似三角形_______组。解: ∵ DE∥BC
∴∠ADE= ∠B,
∠EDC=∠DCB=∠A
① ∵ DE∥BC
∴△ADE ∽ △ABC
② ∵ ∠A= ∠DCB, ∠ADE= ∠B
∴△ADE∽ △CBD
③ ∵ △ADE ∽ △ABC
△ADE ∽ △CBD
∴ △ABC ∽ △CBD
④ ∵ ∠DCA= ∠DCE, ∠A= ∠EDC
∴ △ADC ∽ △DEC1. D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB分析:要证明AC2=AD·AB,需
要先将乘积式改写为比例
式 ,再证明AC、
AD、AB所在的两个三角形相
似。由已知两个三角形有二个
角对应相等,所以两三角形相
似,本题可证。证明:∵ ∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·AB2. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:① △ MAD ~△ MEA ② AM2=MD · ME分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。AM是△ MAD 与△ MEA 的公共边,故是对应边MD、ME的比例中项。证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴ ∠B= ∠MAD
又 ∵ ∠B+ ∠BDM=90°
∠E+ ∠ADE= 90°
∠BDM= ∠ADE∴∠B=∠E
∴∠MAD= ∠E
又 ∵ ∠DMA= ∠AME
∴△MAD∽ △MEA② ∵ △MAD∽ △MEA
∴
即AM2=MD·ME3. 过◇ABCD的一个顶点A作一直线分别交对角线BD、边
BC、边DC的延长线于E、F、G .
求证:EA2 = EF· EG . 分析:要证明
EA2 = EF· EG ,
即 证明 成
立,而EA、EG、EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△AED∽△FEB, △AEB ∽ △GED.证明:∵ AD∥BF AB∥BC
∴△AED ∽△FEB
△AEB ∽△GED
∴
∴4. △ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC(用两种方法证明).证明一:
∵BD⊥AC,CE⊥AB
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°
∴ ∠ABD= ∠ACE
又∵ ∠A= ∠A
∴△ ABD ∽ △ ACE
∴
∵ ∠A= ∠A
∴ △ ADE ∽ △ ABC
证明二:∵ ∠BEO= ∠CDO
∠ BOE=∠COD
∴ △BOE ∽ △COD
∴
即
又∵ ∠BOC= ∠EOD
∴ △BOC ∽△EOD
∴ ∠1= ∠2
∵ ∠1+ ∠BCD=90°,
∠2+ ∠3= ∠ 90°
∴ ∠ BCD= ∠3
又∵ ∠A= ∠A
∴ △ ADE∽ △ ABC6. 已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的
中点,ED交AB的延长线于F. 求证: AB:AC=DF:AF.分析:因△ABC∽△ABD,所以
, 要证
即证 ,
需证△BDF∽△DAF.证明:∵ ∠BAC=90°
AD⊥BC
∴ ∠ABC+∠C= 90°
∠ABC+∠BAD= 90°
∴ ∠BAD= ∠C
∵ ∠ADC= 90°
E是AC的中点,
∴ED=EC
∴ ∠EDC= ∠C
∵ ∠EDC = ∠BDF
∴ ∠BDF= ∠C= ∠BAD
又∵ ∠F =∠F
∴ △BDF∽△DAF.
∴
∵ ∠BAC=90°, AD⊥BC
∴ △ABC∽△ABD
∴
∴
1.已知:如图,△ABC中,P是AB边上的一点,连结CP.满足什么条件时△ ACP∽△ABC. 解:⑴∵∠A= ∠A,∴当∠1= ∠ACB (或∠2= ∠B)时,△ ACP∽△ABC
⑵ ∵∠A= ∠A,∴当AC:AP=AB:AC时,
△ ACP∽△ABC
⑶ ∵∠A= ∠A,
当∠4+∠ACB=180°时, △ ACP∽△ABC答:当∠1= ∠ACB 或∠2= ∠B 或AC:AP=AB:AC或∠4+∠ACB=180°时,△ ACP∽△ABC.1、条件探索型二、探索题2.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似1 这类题型结论是明确的,而需要完备使结论成立的条件.解题思路是:从给定结论出发,通过逆向思考寻求使结论成立的条件. 1.将两块完全相同的等腰直角三角板摆成如图的样子,假设图形中的所有点、线都在同一平面内,则图中有相似(不包括全等)三角形吗?如有,把它们一 一写出来.C解:有相似三角形,它们是:△ADE∽ △BAE, △BAE ∽ △CDA ,△ADE∽ △CDA( △ADE∽ △BAE ∽ △CDA)2、结论探索型2.△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.EEEE 这类题型的特征是有条件而无结论,要确定这些条件下可能出现的结论.解题思路是:从所给条件出发,通过分析、比较、猜想、寻求多种解法和结论,再进行证明. 3、存在探索型 1、 如图, DE是△ABC的中位线,在射线AF上是否存在点M,使△MEC与△ADE相似,若存在,请先确定点 M,再证明这两个三角形相似,若不存在,请说明理由.证明:连结MC, ∵DE是△ABC的中位线, ∴DE∥BC,AE=EC, 又∵ME⊥AC, ∴AM=CM, ∴ ∠1= ∠2 , ∵∠B=90°, ∴ ∠4= ∠B= 90°, ∵AF ∥BC,AM ∥DE, ∴ ∠1= ∠2 , ∴ ∠3= ∠2 , ∵ ∠ADE= ∠MEC=90 ° , ∴ △ADE ∽△MEC.123M解:存在.过点E作AC的垂线,与AF交于一点,即M点(或作∠MCA= ∠AED).4例2、如图,已知:AB⊥DB于点B ,CD⊥DB于点D,AB=6,CD=4,BD=14.
问:在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由。P(2)假设存在这样的点P,使△ABP∽△PDC,则
则有AB:PD=PB:CD设PD=x,则PB=14―x,
∴6: x =(14―x): 4∴x=2或x=12∴x=2或x=12或x=5.6时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似46x14―xDBCAp 所谓存在性问题,一般是要求确定满足某些特定要求的元素有或没有的问题.解题思路是:先假定所需探索的对象存在或结论成立,以此为依据进行计算或推理,若由此推出矛盾,则假定是错误的,从而给出否定的结论,否则给出肯定的证明. ②探究:在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。Q练习:∽ABCDFE三、位似 两个多边形不仅相似,而且对应顶点的连线相交于一点,这样的相似叫做位似,点O叫做位似中心.利用位似的方法,可以把一个多边形放大或缩小
同课章节目录
