浙教版八年级上册 第一章 《三角形的初步知识》章末复习(3)(共19张PPT)
文档属性
| 名称 | 浙教版八年级上册 第一章 《三角形的初步知识》章末复习(3)(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 19:57:35 | ||
图片预览





文档简介
(共19张PPT)
浙教版八年级上册
第一章 三角形的初步知识章末复习
想,一判二推三要使; 写,条分缕析,分步表达
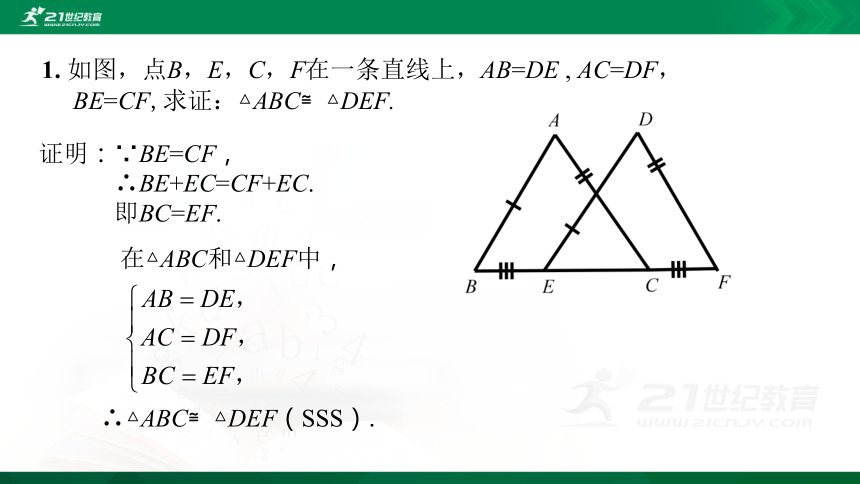
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
1. 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:△ABC≌△DEF.
2. 已知:如图,AB∥CD,∠1=∠2,O为AD中点,EF,
AD交于点O. 求证:O为EF的中点.
分析:
要证O为EF的中点
即证OF=OE
需证△OFD≌△OEA
AB∥CD
OA=OD
∠FOD=∠EOA
∠1=∠2
∠FDO=∠EAO
∠CDA=∠BAD
ASA
易推出
证明:
∵AB∥CD,
∴∠CDA=∠BAD.
又∵∠1=∠2,
∴∠CDA-∠1=∠BAD - ∠2.
即∠FDO=∠EAO.
∵O为AD的中点,
∴OA=OD.
在△OFD和△OEA中,
∴△OFD≌△OEA(ASA).
∴OF=OE.
∴ O是EF的中点.
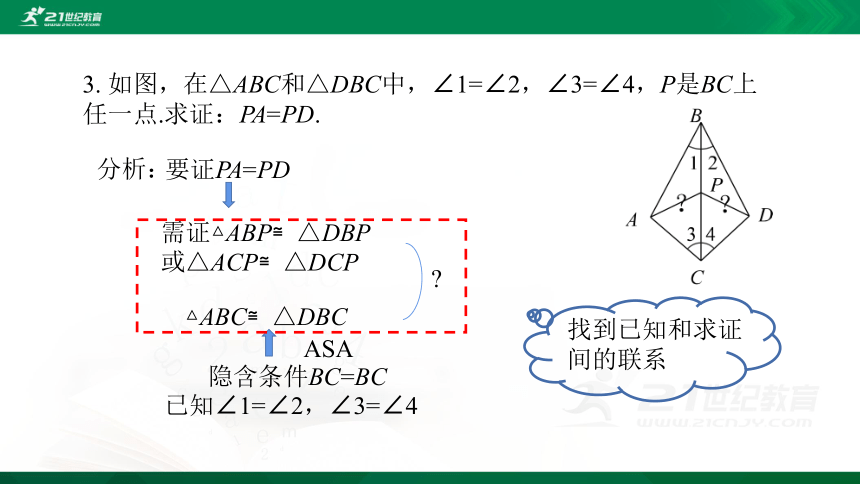
3. 如图,在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任一点.求证:PA=PD.
要证PA=PD
分析:
需证△ABP≌△DBP
或△ACP≌△DCP
已知∠1=∠2,∠3=∠4
隐含条件BC=BC
ASA
△ABC≌△DBC
找到已知和求证
间的联系
证明:
在△ABC和△DBC中,
在△ABP和△DBP中,
∴△ABC≌△DBC(ASA) .
∴AB=DB.
∴△ABP≌△DBP(SAS).
∴PA=PD.
第一次全等为第二次全等提供了条件
要证∠E=∠F.
分析:
需证△ACF≌△ADF
已知AB=CD
AB+BC=CD+BC
AC=BD
已知∠1=∠2
∠ABC=∠BCD=180°
∠ABC-∠1=∠BCD-∠2
∠DBF=∠ACE
SAS
4.如图,点A ,B ,C ,D在一条直线上,且AB=CD,
若∠1=∠2,EC=FB.求证:∠E=∠F.
证明:
∵AB=CD,
∴AB+BC=CD+BC. 即AC=BD.
∵∠ABC=∠BCD=180°,
∠1=∠2 ,
∴∠ABC-∠1=∠BCD-∠2.
即∠DBF=∠ACE.
在△AEC和△DFB中,
∴△AEC≌DFB (SAS).
∴∠E=∠F.
证明:∵FB=CE,
∴FB+FC=CE+FC.
即BC=EF.
∵AB∥ED,
∴∠B=∠E.
∵AC∥FD,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF (ASA).
∴AB=DE , AC=DF.
5. 如图,点B, F, C, E在一条直线上,FB=CE,AB∥ED,
AC∥FD. 求证:AB=DE, AC=DF.
6.四边形ABCD中,AB∥CD,AD∥BC.
求证:AB=CD,AD=BC.
分析:要证AB=CD,AD=BC,连接BD,只要利用ASA,证明△ABD≌△CDB.
四边形ABCD中,AB∥CD,AD∥BC.
求证:AB=CD,AD=BC.
证明:连接BD,
∵AB∥CD, ∴∠DBA=∠BDC. ,∵AD∥BC∴∠ADB=∠CBD.
在△ABD和△CDB中,
∠DBA=∠BDC,
BD=DB,
∠ADB=∠CBD,
∴△ABD≌△CDB. ∴AB=CD,AD=BC.
变式 四边形ABCD中, AB=CD,AD=BC .
求证: AB∥CD,AD∥BC.
分析:要证AB∥CD,AD∥BC ,连接BD,只要利用SSS,证明△ABD≌△CDB.
变式 四边形ABCD中, AB=CD,AB∥CD.
求证:AD=BC ,AD∥BC.
分析:要证AD=BC ,AD∥BC ,连接BD,只要利用SAS,证明△ABD≌△CDB.
7. 在△ABC中,已知∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,
求证:△ADC≌△CEB;DE=AD+BE.
图1
在△ABC中,已知∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于E.
(2)当直线MN绕点C旋转到图2位置时,
求证:DE=AD-BE.
图2
在△ABC中,已知∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于E.
(3)当直线MN绕点C旋转到图3位置时,
试问:DE、AD、BE具有怎样的等量关系?
请写出这个等量关系并加以证明.
图3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版八年级上册
第一章 三角形的初步知识章末复习
想,一判二推三要使; 写,条分缕析,分步表达
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
1. 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:△ABC≌△DEF.
2. 已知:如图,AB∥CD,∠1=∠2,O为AD中点,EF,
AD交于点O. 求证:O为EF的中点.
分析:
要证O为EF的中点
即证OF=OE
需证△OFD≌△OEA
AB∥CD
OA=OD
∠FOD=∠EOA
∠1=∠2
∠FDO=∠EAO
∠CDA=∠BAD
ASA
易推出
证明:
∵AB∥CD,
∴∠CDA=∠BAD.
又∵∠1=∠2,
∴∠CDA-∠1=∠BAD - ∠2.
即∠FDO=∠EAO.
∵O为AD的中点,
∴OA=OD.
在△OFD和△OEA中,
∴△OFD≌△OEA(ASA).
∴OF=OE.
∴ O是EF的中点.
3. 如图,在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任一点.求证:PA=PD.
要证PA=PD
分析:
需证△ABP≌△DBP
或△ACP≌△DCP
已知∠1=∠2,∠3=∠4
隐含条件BC=BC
ASA
△ABC≌△DBC
找到已知和求证
间的联系
证明:
在△ABC和△DBC中,
在△ABP和△DBP中,
∴△ABC≌△DBC(ASA) .
∴AB=DB.
∴△ABP≌△DBP(SAS).
∴PA=PD.
第一次全等为第二次全等提供了条件
要证∠E=∠F.
分析:
需证△ACF≌△ADF
已知AB=CD
AB+BC=CD+BC
AC=BD
已知∠1=∠2
∠ABC=∠BCD=180°
∠ABC-∠1=∠BCD-∠2
∠DBF=∠ACE
SAS
4.如图,点A ,B ,C ,D在一条直线上,且AB=CD,
若∠1=∠2,EC=FB.求证:∠E=∠F.
证明:
∵AB=CD,
∴AB+BC=CD+BC. 即AC=BD.
∵∠ABC=∠BCD=180°,
∠1=∠2 ,
∴∠ABC-∠1=∠BCD-∠2.
即∠DBF=∠ACE.
在△AEC和△DFB中,
∴△AEC≌DFB (SAS).
∴∠E=∠F.
证明:∵FB=CE,
∴FB+FC=CE+FC.
即BC=EF.
∵AB∥ED,
∴∠B=∠E.
∵AC∥FD,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF (ASA).
∴AB=DE , AC=DF.
5. 如图,点B, F, C, E在一条直线上,FB=CE,AB∥ED,
AC∥FD. 求证:AB=DE, AC=DF.
6.四边形ABCD中,AB∥CD,AD∥BC.
求证:AB=CD,AD=BC.
分析:要证AB=CD,AD=BC,连接BD,只要利用ASA,证明△ABD≌△CDB.
四边形ABCD中,AB∥CD,AD∥BC.
求证:AB=CD,AD=BC.
证明:连接BD,
∵AB∥CD, ∴∠DBA=∠BDC. ,∵AD∥BC∴∠ADB=∠CBD.
在△ABD和△CDB中,
∠DBA=∠BDC,
BD=DB,
∠ADB=∠CBD,
∴△ABD≌△CDB. ∴AB=CD,AD=BC.
变式 四边形ABCD中, AB=CD,AD=BC .
求证: AB∥CD,AD∥BC.
分析:要证AB∥CD,AD∥BC ,连接BD,只要利用SSS,证明△ABD≌△CDB.
变式 四边形ABCD中, AB=CD,AB∥CD.
求证:AD=BC ,AD∥BC.
分析:要证AD=BC ,AD∥BC ,连接BD,只要利用SAS,证明△ABD≌△CDB.
7. 在△ABC中,已知∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,
求证:△ADC≌△CEB;DE=AD+BE.
图1
在△ABC中,已知∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于E.
(2)当直线MN绕点C旋转到图2位置时,
求证:DE=AD-BE.
图2
在△ABC中,已知∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于E.
(3)当直线MN绕点C旋转到图3位置时,
试问:DE、AD、BE具有怎样的等量关系?
请写出这个等量关系并加以证明.
图3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
