1.4 二次函数的应用 同步练习(含答案)
文档属性
| 名称 | 1.4 二次函数的应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 13:54:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.4 二次函数的应用
一、单选题
1.(2024九上·梧州月考)如表是一组二次函数y=x2﹣x﹣3的自变量和函数值的关系,那么方程x2﹣x﹣3=0的一个近似根是( )
x 1 2 3 4
y ﹣3 ﹣1 3 9
A.1.2 B.2.3 C.3.4 D.4.5
2.(2023九上·利州期中)某旅行社有100张床位,每张床位每晚收费10元时,客床可全部租出,若每张床每晚收费提高2元,则减少10张床位的租出;若每张床每晚收费再提高2元,则再减少10张床位的租出;以每次提高2元的这种方法变化下去,为了投资少而获利大,每张床每晚应提高( )
A.4元或16元 B.4元 C.6元 D.8元
3.(2020七下·深圳期中)长方形的周长为24cm,其中一边为xcm(其中 x>0),面积为 ,则这样的长方形中y与x的关系可以写为( )
A. B.
C. D.
4.(2025九上·新吴期末)根据下列表格对应值:
x
判断关于x的方程的一个解x的范围是( )
A. B. C. D.
5.(2024九上·麒麟期中)为了备战云南省第二届青少年运动会,小路对自己实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为,由此可知小路此次实心球训练的成绩为( )
A. B. C. D.
6.(2020·宁波模拟)已知一个直角三角形的两边长分别为a和5,第三边长是抛物线y=x -10x+21与x轴交点间的距离,则a的值为( )
A.3 B. C.3或 D.不能确定
7.(2023·涟水模拟)二次函数的顶点坐标为,其部分图像如图所示,下面结论错误的是( )
A.
B.
C.关于x的方程没有实数根
D.关于x的方程的负实数根取值范围为:
8.用一根长为40cm的绳子围成一个面积为a(cm2)的长方形,则a的值不可能为( ).
A.60 B.80 C.100 D.120
9.(2023九上·埇桥月考)根据下列表格对应值,判断关于的方程的一个解的范围是( )
1.1 1.2 1.3 1.4
-0.59 0.84 2.29 3.76
A.1.1<x<1.2 B.1.2<x<1.3 C.1.3<x<1.4 D.无法判定
10.(2018·南岗模拟)如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
A. B.
C. D.
二、填空题
11.(2024九上·海口期末)黄冈中学是百年名校,百年校庆上的焰火晚会令很多人记忆犹新.有一种焰火升高高度为h(m)与飞行时间t(s)的关系式是,若这种焰火在点燃升空后到最高处引爆,则从点火到引爆所需时间为 s.
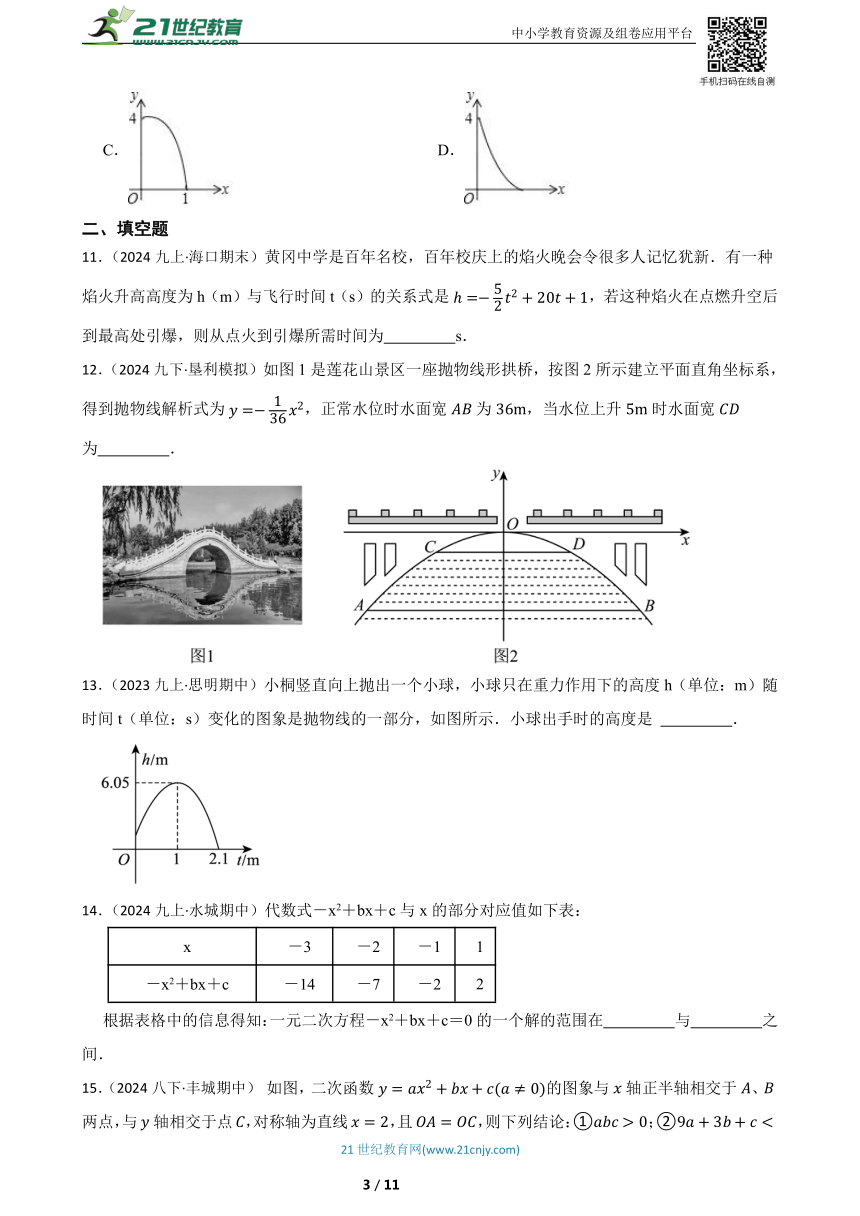
12.(2024九下·垦利模拟)如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线解析式为,正常水位时水面宽为,当水位上升时水面宽为 .
13.(2023九上·思明期中)小桐竖直向上抛出一个小球,小球只在重力作用下的高度h(单位:m)随时间t(单位:s)变化的图象是抛物线的一部分,如图所示.小球出手时的高度是 .
14.(2024九上·水城期中)代数式-x2+bx+c与x的部分对应值如下表:
x -3 -2 -1 1
-x2+bx+c -14 -7 -2 2
根据表格中的信息得知:一元二次方程-x2+bx+c=0的一个解的范围在 与 之间.
15.(2024八下·丰城期中) 如图,二次函数的图象与轴正半轴相交于、两点,与轴相交于点,对称轴为直线,且,则下列结论:①;②;③;④关于的方程有一个根为,其中正确的结论个数有 个.
16.(2024九上·栖霞月考)已知关于x的一元二次方程的两根分别为x1,x2,且﹣1<x1<0,2<x2<3,则实数a的取值范围是 .
三、计算题
17.(2024九上·宜春期中)某商家出售的一种商品成本价为元/千克,市场调查发现,该商品每天的销售量y(千克)与售价x(元/千克)满足一次函数.设这种商品每天的销售利润为w元.
(1)求w关于x的函数解析式;
(2)该商品售价定为每千克多少元时,每天的销售利润最大?最大销售利润是多少?
18.(2024九上·南乐期末)在杭州举办的亚运会令世界瞩目,吉祥物“琮琮”、“莲莲”、“宸宸”家喻户晓,其相关产品成为热销产品.某商店购进了一批吉祥物毛绒玩具,进价为每个元.若毛绒玩具每个的售价是元时,每天可售出个;若每个售价提高元,则每天少卖个.
(1)设该吉祥物毛绒玩具每个售价定为元,求该商品销售量与之间的函数关系式;
(2)如果每天的利润要达到元,并且尽可能让利于顾客,每个毛绒玩具售价应定为多少元?
(3)若获利不得高于进价的,每个毛绒玩具售价定为多少元时,每天销售玩具所获利润最大,最大利润是多少元?
19.(2022九上·长沙开学考)对于实数a和b,定义新运算“@”:a@b=
(1)计算20182018@(8@28)的值;
(2)若(x﹣1)@(3﹣2x)=2,求实数x的值;
(3)设函数y1=(2﹣x2)@(4x﹣x2),若函数y2=y1﹣m的图象与x轴恰有两个交点,求实数m的取值范围.
四、解答题
20.(2023九上·福州月考)一人一盔安全守规,一人一戴平安常在,某电动自行车配件店经市场调查,发现进价为40元的新款头盔每月的销售量y(件)与售价x(元)成一次函数关系y=﹣2x+400.
(1)若物价局规定,该头盔最高售价不得超过100元,当售价为多少元时,利润达到5600元;
(2)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大?最大利润是多少元?
21.(2025九上·惠阳期末)某种服装每天可销售20件,每件盈利44元.若每件降价1元,则每天可多销售5件.根据题意,完成下列问题
(1)填空:当每件盈利42元时,每天销售量为______件,每天盈利______元;
(2)设每件降价元,则每件盈利______元,每天销售量为______件;若每天盈利1600元,求的值.
22.(2024九下·启东模拟)为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 乙 丙
单价(元/棵) 14 16 28
合理用地(m2/棵) 0.4 1 0.4
23.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
答案解析部分
1.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
2.【答案】C
【知识点】二次函数的实际应用-销售问题
3.【答案】C
【知识点】二次函数的实际应用-几何问题
4.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
5.【答案】B
【知识点】二次函数的实际应用-抛球问题
6.【答案】C
【知识点】二次函数的实际应用-几何问题
7.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数与一元二次方程的综合应用
8.【答案】D
【知识点】二次函数的实际应用-几何问题
9.【答案】C
【知识点】利用二次函数图象求一元二次方程的近似根
10.【答案】D
【知识点】二次函数的实际应用-几何问题
11.【答案】4
【知识点】二次函数的实际应用-抛球问题
12.【答案】
【知识点】二次函数的实际应用-拱桥问题
13.【答案】1.05m
【知识点】待定系数法求二次函数解析式;通过函数图象获取信息;二次函数的实际应用-抛球问题
14.【答案】-1;1
【知识点】利用二次函数图象判断一元二次方程根的情况
15.【答案】3
【知识点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;利用二次函数图象判断一元二次方程根的情况
16.【答案】
【知识点】利用二次函数图象判断一元二次方程根的情况
17.【答案】(1)
(2)该商品售价定为每千克元时,每天的销售利润最大,最大销售利润是元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
18.【答案】(1)
(2)
(3)定为元时,每天销售毛绒玩具所获利润最大,最大利润是元
【知识点】一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题;一次函数的其他应用
19.【答案】(1)20181982;(2)x=0或2;(3)m<4.
【知识点】利用二次函数图象判断一元二次方程根的情况
20.【答案】(1)解:依题意得(x﹣40)(﹣2x+400)=5600,
整理得:x2﹣240x+10800=0,
解得x=60或180,
∵物价局规定,该头盔最高售价不得超过100元,
∴x=180不合题意舍去,
答:当售价为60元时,利润达到5600元.
(2)解:设利润为W元,则W=(x﹣40)(﹣2x+400)=﹣2(x﹣120)2+12800,
∵40×(1+80%)=72,
x≤72,
∵﹣2<0,
∴当x=72时,W最大=8192,
答:售价定为72元时,月销售利润最大为8192元.
【知识点】一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
21.【答案】(1)30,
(2),,4元或36元
【知识点】有理数的加减乘除混合运算的法则;二次函数的实际应用-销售问题
22.【答案】(1)y=﹣2x2+36x(0【知识点】二次函数的实际应用-几何问题
23.【答案】解:(1)∵y=x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=﹣3,即A点坐标为(﹣3,0),
当x=0时,y=3,即B点坐标为(0,3),
将A(﹣3,0),B(0,3)代入y=﹣x2+bx+c,
得,
解得,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)如图1,设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),则m<0,﹣m2﹣2m+3<0.
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴对称轴为直线x=﹣1,顶点D的坐标为(﹣1,4),
设抛物线的对称轴与x轴交于点G,连接FG,则G(﹣1,0),AG=2.
∵直线AB的解析式为y=x+3,
∴当x=﹣1时,y=﹣1+3=2,
∴E点坐标为(﹣1,2).
∵S△AEF=S△AEG+S△AFG﹣S△EFG=×2×2+×2×(m2+2m﹣3)﹣×2×(﹣1﹣m)=m2+3m,
∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,
解得m1=,m2=(舍去),
当m=时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=,
∴点F的坐标为(,);
(3)设P点坐标为(﹣1,n).
∵B(0,3),C(1,0),
∴BC2=12+32=10.
分三种情况:
①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,
即(0+1)2+(n﹣3)2+10=(1+1)2+(n﹣0)2,
化简整理得6n=16,解得n=,
∴P点坐标为(﹣1,),
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣=,
∵点P的速度为每秒1个单位长度,
∴t1=;
②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,
即(0+1)2+(n﹣3)2+(1+1)2+(n﹣0)2=10,
化简整理得n2﹣3n+2=0,解得n=2或1,
∴P点坐标为(﹣1,2)或(﹣1,1),
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣2=2或PD=4﹣1=3,
∵点P的速度为每秒1个单位长度,
∴t2=2,t3=3;
③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,
即10+(1+1)2+(n﹣0)2=(0+1)2+(n﹣3)2,
化简整理得6n=﹣4,解得n=﹣,
∴P点坐标为(﹣1,﹣),
∵顶点D的坐标为(﹣1,4),
∴PD=4+=,
∵点P的速度为每秒1个单位长度,
∴t4=;
综上可知,当t为秒或2秒或3秒或秒时,以P、B、C为顶点的三角形是直角三角形.
【知识点】二次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 11
1.4 二次函数的应用
一、单选题
1.(2024九上·梧州月考)如表是一组二次函数y=x2﹣x﹣3的自变量和函数值的关系,那么方程x2﹣x﹣3=0的一个近似根是( )
x 1 2 3 4
y ﹣3 ﹣1 3 9
A.1.2 B.2.3 C.3.4 D.4.5
2.(2023九上·利州期中)某旅行社有100张床位,每张床位每晚收费10元时,客床可全部租出,若每张床每晚收费提高2元,则减少10张床位的租出;若每张床每晚收费再提高2元,则再减少10张床位的租出;以每次提高2元的这种方法变化下去,为了投资少而获利大,每张床每晚应提高( )
A.4元或16元 B.4元 C.6元 D.8元
3.(2020七下·深圳期中)长方形的周长为24cm,其中一边为xcm(其中 x>0),面积为 ,则这样的长方形中y与x的关系可以写为( )
A. B.
C. D.
4.(2025九上·新吴期末)根据下列表格对应值:
x
判断关于x的方程的一个解x的范围是( )
A. B. C. D.
5.(2024九上·麒麟期中)为了备战云南省第二届青少年运动会,小路对自己实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为,由此可知小路此次实心球训练的成绩为( )
A. B. C. D.
6.(2020·宁波模拟)已知一个直角三角形的两边长分别为a和5,第三边长是抛物线y=x -10x+21与x轴交点间的距离,则a的值为( )
A.3 B. C.3或 D.不能确定
7.(2023·涟水模拟)二次函数的顶点坐标为,其部分图像如图所示,下面结论错误的是( )
A.
B.
C.关于x的方程没有实数根
D.关于x的方程的负实数根取值范围为:
8.用一根长为40cm的绳子围成一个面积为a(cm2)的长方形,则a的值不可能为( ).
A.60 B.80 C.100 D.120
9.(2023九上·埇桥月考)根据下列表格对应值,判断关于的方程的一个解的范围是( )
1.1 1.2 1.3 1.4
-0.59 0.84 2.29 3.76
A.1.1<x<1.2 B.1.2<x<1.3 C.1.3<x<1.4 D.无法判定
10.(2018·南岗模拟)如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
A. B.
C. D.
二、填空题
11.(2024九上·海口期末)黄冈中学是百年名校,百年校庆上的焰火晚会令很多人记忆犹新.有一种焰火升高高度为h(m)与飞行时间t(s)的关系式是,若这种焰火在点燃升空后到最高处引爆,则从点火到引爆所需时间为 s.
12.(2024九下·垦利模拟)如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线解析式为,正常水位时水面宽为,当水位上升时水面宽为 .
13.(2023九上·思明期中)小桐竖直向上抛出一个小球,小球只在重力作用下的高度h(单位:m)随时间t(单位:s)变化的图象是抛物线的一部分,如图所示.小球出手时的高度是 .
14.(2024九上·水城期中)代数式-x2+bx+c与x的部分对应值如下表:
x -3 -2 -1 1
-x2+bx+c -14 -7 -2 2
根据表格中的信息得知:一元二次方程-x2+bx+c=0的一个解的范围在 与 之间.
15.(2024八下·丰城期中) 如图,二次函数的图象与轴正半轴相交于、两点,与轴相交于点,对称轴为直线,且,则下列结论:①;②;③;④关于的方程有一个根为,其中正确的结论个数有 个.
16.(2024九上·栖霞月考)已知关于x的一元二次方程的两根分别为x1,x2,且﹣1<x1<0,2<x2<3,则实数a的取值范围是 .
三、计算题
17.(2024九上·宜春期中)某商家出售的一种商品成本价为元/千克,市场调查发现,该商品每天的销售量y(千克)与售价x(元/千克)满足一次函数.设这种商品每天的销售利润为w元.
(1)求w关于x的函数解析式;
(2)该商品售价定为每千克多少元时,每天的销售利润最大?最大销售利润是多少?
18.(2024九上·南乐期末)在杭州举办的亚运会令世界瞩目,吉祥物“琮琮”、“莲莲”、“宸宸”家喻户晓,其相关产品成为热销产品.某商店购进了一批吉祥物毛绒玩具,进价为每个元.若毛绒玩具每个的售价是元时,每天可售出个;若每个售价提高元,则每天少卖个.
(1)设该吉祥物毛绒玩具每个售价定为元,求该商品销售量与之间的函数关系式;
(2)如果每天的利润要达到元,并且尽可能让利于顾客,每个毛绒玩具售价应定为多少元?
(3)若获利不得高于进价的,每个毛绒玩具售价定为多少元时,每天销售玩具所获利润最大,最大利润是多少元?
19.(2022九上·长沙开学考)对于实数a和b,定义新运算“@”:a@b=
(1)计算20182018@(8@28)的值;
(2)若(x﹣1)@(3﹣2x)=2,求实数x的值;
(3)设函数y1=(2﹣x2)@(4x﹣x2),若函数y2=y1﹣m的图象与x轴恰有两个交点,求实数m的取值范围.
四、解答题
20.(2023九上·福州月考)一人一盔安全守规,一人一戴平安常在,某电动自行车配件店经市场调查,发现进价为40元的新款头盔每月的销售量y(件)与售价x(元)成一次函数关系y=﹣2x+400.
(1)若物价局规定,该头盔最高售价不得超过100元,当售价为多少元时,利润达到5600元;
(2)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大?最大利润是多少元?
21.(2025九上·惠阳期末)某种服装每天可销售20件,每件盈利44元.若每件降价1元,则每天可多销售5件.根据题意,完成下列问题
(1)填空:当每件盈利42元时,每天销售量为______件,每天盈利______元;
(2)设每件降价元,则每件盈利______元,每天销售量为______件;若每天盈利1600元,求的值.
22.(2024九下·启东模拟)为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 乙 丙
单价(元/棵) 14 16 28
合理用地(m2/棵) 0.4 1 0.4
23.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
答案解析部分
1.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
2.【答案】C
【知识点】二次函数的实际应用-销售问题
3.【答案】C
【知识点】二次函数的实际应用-几何问题
4.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
5.【答案】B
【知识点】二次函数的实际应用-抛球问题
6.【答案】C
【知识点】二次函数的实际应用-几何问题
7.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数与一元二次方程的综合应用
8.【答案】D
【知识点】二次函数的实际应用-几何问题
9.【答案】C
【知识点】利用二次函数图象求一元二次方程的近似根
10.【答案】D
【知识点】二次函数的实际应用-几何问题
11.【答案】4
【知识点】二次函数的实际应用-抛球问题
12.【答案】
【知识点】二次函数的实际应用-拱桥问题
13.【答案】1.05m
【知识点】待定系数法求二次函数解析式;通过函数图象获取信息;二次函数的实际应用-抛球问题
14.【答案】-1;1
【知识点】利用二次函数图象判断一元二次方程根的情况
15.【答案】3
【知识点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;利用二次函数图象判断一元二次方程根的情况
16.【答案】
【知识点】利用二次函数图象判断一元二次方程根的情况
17.【答案】(1)
(2)该商品售价定为每千克元时,每天的销售利润最大,最大销售利润是元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
18.【答案】(1)
(2)
(3)定为元时,每天销售毛绒玩具所获利润最大,最大利润是元
【知识点】一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题;一次函数的其他应用
19.【答案】(1)20181982;(2)x=0或2;(3)m<4.
【知识点】利用二次函数图象判断一元二次方程根的情况
20.【答案】(1)解:依题意得(x﹣40)(﹣2x+400)=5600,
整理得:x2﹣240x+10800=0,
解得x=60或180,
∵物价局规定,该头盔最高售价不得超过100元,
∴x=180不合题意舍去,
答:当售价为60元时,利润达到5600元.
(2)解:设利润为W元,则W=(x﹣40)(﹣2x+400)=﹣2(x﹣120)2+12800,
∵40×(1+80%)=72,
x≤72,
∵﹣2<0,
∴当x=72时,W最大=8192,
答:售价定为72元时,月销售利润最大为8192元.
【知识点】一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
21.【答案】(1)30,
(2),,4元或36元
【知识点】有理数的加减乘除混合运算的法则;二次函数的实际应用-销售问题
22.【答案】(1)y=﹣2x2+36x(0
23.【答案】解:(1)∵y=x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=﹣3,即A点坐标为(﹣3,0),
当x=0时,y=3,即B点坐标为(0,3),
将A(﹣3,0),B(0,3)代入y=﹣x2+bx+c,
得,
解得,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)如图1,设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),则m<0,﹣m2﹣2m+3<0.
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴对称轴为直线x=﹣1,顶点D的坐标为(﹣1,4),
设抛物线的对称轴与x轴交于点G,连接FG,则G(﹣1,0),AG=2.
∵直线AB的解析式为y=x+3,
∴当x=﹣1时,y=﹣1+3=2,
∴E点坐标为(﹣1,2).
∵S△AEF=S△AEG+S△AFG﹣S△EFG=×2×2+×2×(m2+2m﹣3)﹣×2×(﹣1﹣m)=m2+3m,
∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,
解得m1=,m2=(舍去),
当m=时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=,
∴点F的坐标为(,);
(3)设P点坐标为(﹣1,n).
∵B(0,3),C(1,0),
∴BC2=12+32=10.
分三种情况:
①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,
即(0+1)2+(n﹣3)2+10=(1+1)2+(n﹣0)2,
化简整理得6n=16,解得n=,
∴P点坐标为(﹣1,),
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣=,
∵点P的速度为每秒1个单位长度,
∴t1=;
②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,
即(0+1)2+(n﹣3)2+(1+1)2+(n﹣0)2=10,
化简整理得n2﹣3n+2=0,解得n=2或1,
∴P点坐标为(﹣1,2)或(﹣1,1),
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣2=2或PD=4﹣1=3,
∵点P的速度为每秒1个单位长度,
∴t2=2,t3=3;
③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,
即10+(1+1)2+(n﹣0)2=(0+1)2+(n﹣3)2,
化简整理得6n=﹣4,解得n=﹣,
∴P点坐标为(﹣1,﹣),
∵顶点D的坐标为(﹣1,4),
∴PD=4+=,
∵点P的速度为每秒1个单位长度,
∴t4=;
综上可知,当t为秒或2秒或3秒或秒时,以P、B、C为顶点的三角形是直角三角形.
【知识点】二次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 11
同课章节目录
