1.1.1认识三角形 教案
图片预览
文档简介
中小学教育资源及组卷应用平台
分课时教学设计
第1课时《1.1.1认识三角形 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 结合生活实际引入教学，激发学生的学习兴趣，理解三角形三边关系的性质，并会初步应用它们来解决问题．
学习者分析 掌握三角形的分类，通过观察、操作、想象、推理、交流等活动，发展空间观念和推理能力.
教学目标 1、结合具体实例，进一步认识三角形的概念及基本要素。 2、理解三角形三边关系的性质，并会初步应用它们来解决问题。 3、通过观察、操作、想象、推理、交流等活动，发展空间观念和推理能力。
教学重点 三角形任何两边的和大于第三边，任何两边之差小于第三边”的性质。
教学难点 判断三条线段能否组成三角形，过程较为复杂，是本节教学的难点。
学习活动设计
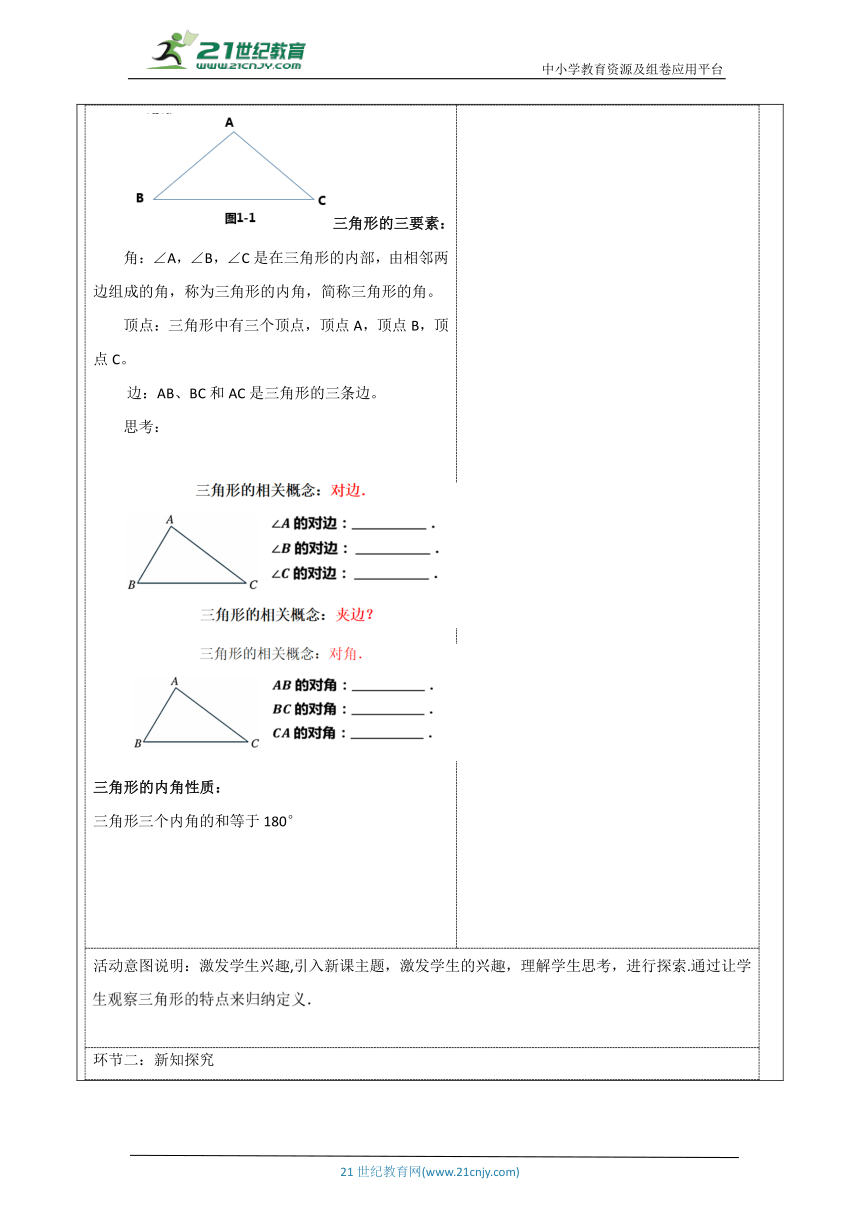
教师活动学生活动环节一：引入新课 在这座铁塔上我们可以看到许多三角形的支架，你能举出在生活中看到的三角形的例子吗？ 那么，怎样的图形叫做三角形呢 三角形的三要素： 角：∠A，∠B，∠C是在三角形的内部，由相邻两边组成的角，称为三角形的内角，简称三角形的角。 顶点：三角形中有三个顶点，顶点A，顶点B，顶点C。 边：AB、BC和AC是三角形的三条边。 思考： 三角形的内角性质： 三角形三个内角的和等于180° 学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，进行探索.通过让学生观察三角形的特点来归纳定义． 环节二：新知探究教师活动2： 思考：说出图中所有的三角形，以及每一个三角形的三条边和三个内角。 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．通过观察、操作、想象、推理、交流等活动，发展空间观念和推理能力。 环节三：典例精析 【例1】判断下列各组线段中，哪些首尾相接能组成三角形，哪些不能组成三角形，并说明理由. (1)a=2.5 cm，b=3cm，c=5cm (2)e=6.3cm，f=6.3cm，g=12.6cm 解(1):最长线段是c=5cm，a+b=2.5+3=5.5(cm) ∴a+b＞c，所以线段a，b，c能组成三角形 (2)∵最长线段是g=12.6cm e+f=6.3+6.3=12.6(cm), e+f=g，所以线段e，f，g不能组成三角形 计算每个三角形的任意两边之差，并与第三边比较，你能得到什么结论？小组交流。 ︳两边之差︳< 第三边 <两边之和 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，掌握三角形任何两边的和大于第三边，任何两边之差小于第三边”的性质．
板书设计
课堂练习 【知识技能类作业】 必做题： 1.若某三角形的两边长分别为3和4，则下列长度的线段能作为其第三边的是( ) A.1 B.5 C.7 D.9 选做题： 2.在直角三角形ABC中，∠A=2∠B，则∠A= 度，∠B= 度. 【综合拓展类作业】 3.已知△ABC的三边长分别是a、b、c，化简|a+b-c|-|b-a-c|=______．
课堂总结
作业设计 【知识技能类作业】 必做题： 1.图中共有______个三角形，分别是__________________________； 以∠C为内角的三角形是__________________， 在这些三角形中，∠C的对边分别为___________． 选做题： 2.如图，在△BCD中，BC＝4，BD＝5. (1)求CD的取值范围； (2)若AE∥BD，∠A＝55°，∠BDE＝125°，求∠C的度数． 解：（1）∵在△BCD中，BC＝4，BD＝5，∴1＜DC＜9. （2）∵AE∥BD，∠BDE＝125°， ∴∠AEC＝180°－∠BDE＝55°， 又∵∠A＝55°，∴∠C＝180°－55°－55°＝70°. 【综合拓展类作业】 3.如图，在小河的同侧有A,B,C三个村庄，图中的线段表示道路，某邮递员从A村送信到B村，总是走经过C村的道路，不走经过D村的道路，这是为什么呢？请利用你所学的数学知识加以证明．
教学反思
21世纪教育网(www.21cnjy.com)
分课时教学设计
第1课时《1.1.1认识三角形 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 结合生活实际引入教学，激发学生的学习兴趣，理解三角形三边关系的性质，并会初步应用它们来解决问题．
学习者分析 掌握三角形的分类，通过观察、操作、想象、推理、交流等活动，发展空间观念和推理能力.
教学目标 1、结合具体实例，进一步认识三角形的概念及基本要素。 2、理解三角形三边关系的性质，并会初步应用它们来解决问题。 3、通过观察、操作、想象、推理、交流等活动，发展空间观念和推理能力。
教学重点 三角形任何两边的和大于第三边，任何两边之差小于第三边”的性质。
教学难点 判断三条线段能否组成三角形，过程较为复杂，是本节教学的难点。
学习活动设计
教师活动学生活动环节一：引入新课 在这座铁塔上我们可以看到许多三角形的支架，你能举出在生活中看到的三角形的例子吗？ 那么，怎样的图形叫做三角形呢 三角形的三要素： 角：∠A，∠B，∠C是在三角形的内部，由相邻两边组成的角，称为三角形的内角，简称三角形的角。 顶点：三角形中有三个顶点，顶点A，顶点B，顶点C。 边：AB、BC和AC是三角形的三条边。 思考： 三角形的内角性质： 三角形三个内角的和等于180° 学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，进行探索.通过让学生观察三角形的特点来归纳定义． 环节二：新知探究教师活动2： 思考：说出图中所有的三角形，以及每一个三角形的三条边和三个内角。 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．通过观察、操作、想象、推理、交流等活动，发展空间观念和推理能力。 环节三：典例精析 【例1】判断下列各组线段中，哪些首尾相接能组成三角形，哪些不能组成三角形，并说明理由. (1)a=2.5 cm，b=3cm，c=5cm (2)e=6.3cm，f=6.3cm，g=12.6cm 解(1):最长线段是c=5cm，a+b=2.5+3=5.5(cm) ∴a+b＞c，所以线段a，b，c能组成三角形 (2)∵最长线段是g=12.6cm e+f=6.3+6.3=12.6(cm), e+f=g，所以线段e，f，g不能组成三角形 计算每个三角形的任意两边之差，并与第三边比较，你能得到什么结论？小组交流。 ︳两边之差︳< 第三边 <两边之和 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，掌握三角形任何两边的和大于第三边，任何两边之差小于第三边”的性质．
板书设计
课堂练习 【知识技能类作业】 必做题： 1.若某三角形的两边长分别为3和4，则下列长度的线段能作为其第三边的是( ) A.1 B.5 C.7 D.9 选做题： 2.在直角三角形ABC中，∠A=2∠B，则∠A= 度，∠B= 度. 【综合拓展类作业】 3.已知△ABC的三边长分别是a、b、c，化简|a+b-c|-|b-a-c|=______．
课堂总结
作业设计 【知识技能类作业】 必做题： 1.图中共有______个三角形，分别是__________________________； 以∠C为内角的三角形是__________________， 在这些三角形中，∠C的对边分别为___________． 选做题： 2.如图，在△BCD中，BC＝4，BD＝5. (1)求CD的取值范围； (2)若AE∥BD，∠A＝55°，∠BDE＝125°，求∠C的度数． 解：（1）∵在△BCD中，BC＝4，BD＝5，∴1＜DC＜9. （2）∵AE∥BD，∠BDE＝125°， ∴∠AEC＝180°－∠BDE＝55°， 又∵∠A＝55°，∴∠C＝180°－55°－55°＝70°. 【综合拓展类作业】 3.如图，在小河的同侧有A,B,C三个村庄，图中的线段表示道路，某邮递员从A村送信到B村，总是走经过C村的道路，不走经过D村的道路，这是为什么呢？请利用你所学的数学知识加以证明．
教学反思
21世纪教育网(www.21cnjy.com)
同课章节目录