2.2 简单事件的概率 同步练习(含答案)
文档属性
| 名称 | 2.2 简单事件的概率 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 339.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:09:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.2 简单事件的概率
一、单选题
1.(2024九下·香坊模拟)小明、小红、小刚3位同学合影留念,3人随机站成一排,那么小明、小刚两人恰好相邻的概率是( ).
A. B. C. D.
2.(2020九上·广东期末)某地质学家预测:在未来的20年内,F市发生地震的概率是 .以下叙述正确的是( )
A.从现在起经过13至14年F市将会发生一次地震
B.可以确定F市在未来20年内将会发生一次地震
C.未来20年内,F市发生地震的可能性比没有发生地震的可能性大
D.我们不能判断未来会发生什么事,因此没有人可以确定何时会有地震发生
3.(2023九上·温州期中)现有三张正面分别印有2023年杭州亚运会吉祥物“琮琮”、“宸宸”和“莲莲”的不透明卡片,卡片除正面图案不同外,其余均相同.将三张卡片正面向下,从中随机抽取一张是“琮琮”的概率是( )
A. B. C. D.
4.(2024九上·宣汉期末)一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为( )
A. B. C. D.
5.(2024九上·顺德期中)用如图所示的两个可自由转动的转盘做“配紫色”游戏(红色和蓝色配成紫色),那么转盘停止时指针所指的颜色可配成紫色的概率是( )
A. B. C. D.
6.经过某十字路口的汽车,它可能继续直行,也可能向左或向右转.若这三种可能性相同,则甲、乙两辆汽车经过该十字路口都继续直行的概率为( )
A. B. C. D.
7.如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
A. B. C. D.
8.若一个不透明的袋子中装有2个白球、3个黄球和1个红球,这些球除颜色外其他完全相同,则从袋子中随机摸出一个球是白球的概率为( )
A. B. C. D.
9.(2019·三亚模拟)在1,2,3三个数中任取两个,组成一个两位数,则组成的两位数是偶数的概率为()
A. B. C. D.
10.(2023·永嘉模拟)甲乙丙丁四人互相给其他三人之一写信,选择对象的方式等可能.问存在两个人收到对方的信的概率( )
A. B. C. D.
二、填空题
11.(2018·天津)不透明袋子中装有11个球,其中有6个红球,3个黄球,2个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .
12.(2025·建始模拟)现有分别标有汉字“爱”“我”“中”“华”的四张卡片,它们除汉字外无其他差别.若把四张卡片背面朝上,洗匀放在桌子上,然后任意抽取一张卡片,不放回,再任意抽取一张,则两次抽取的卡片上的汉字能组成“中华”的概率是 .
13.(2024七下·东营期中)一个不透明的袋中装有除颜色外均相同的8个红球和m个黄球,从中随机摸出一个,摸到红球的概率为,则m= .
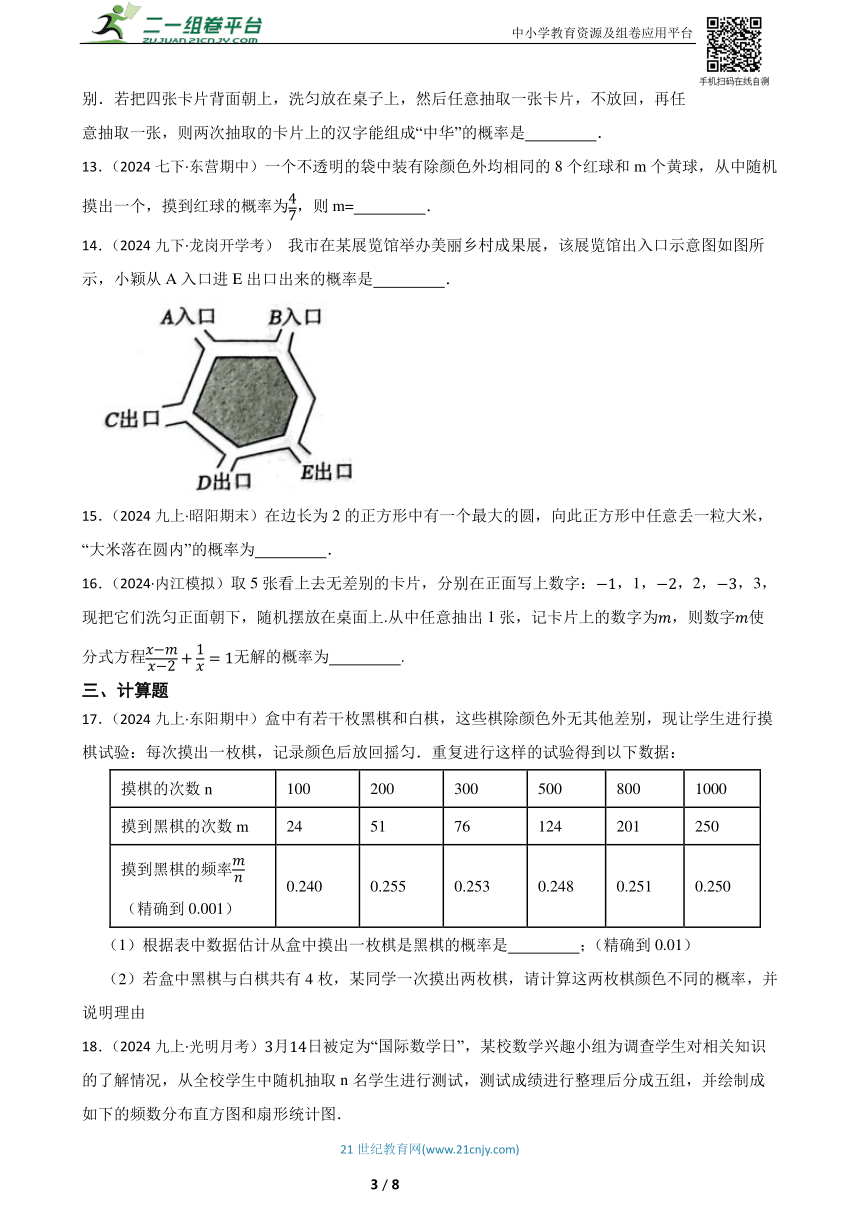
14.(2024九下·龙岗开学考) 我市在某展览馆举办美丽乡村成果展,该展览馆出入口示意图如图所示,小颖从A入口进E出口出来的概率是 .
15.(2024九上·昭阳期末)在边长为2的正方形中有一个最大的圆,向此正方形中任意丢一粒大米,“大米落在圆内”的概率为 .
16.(2024·内江模拟)取5张看上去无差别的卡片,分别在正面写上数字:,1,,2,,3,现把它们洗匀正面朝下,随机摆放在桌面上.从中任意抽出1张,记卡片上的数字为,则数字使分式方程无解的概率为 .
三、计算题
17.(2024九上·东阳期中)盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n 100 200 300 500 800 1000
摸到黑棋的次数m 24 51 76 124 201 250
摸到黑棋的频率(精确到0.001) 0.240 0.255 0.253 0.248 0.251 0.250
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
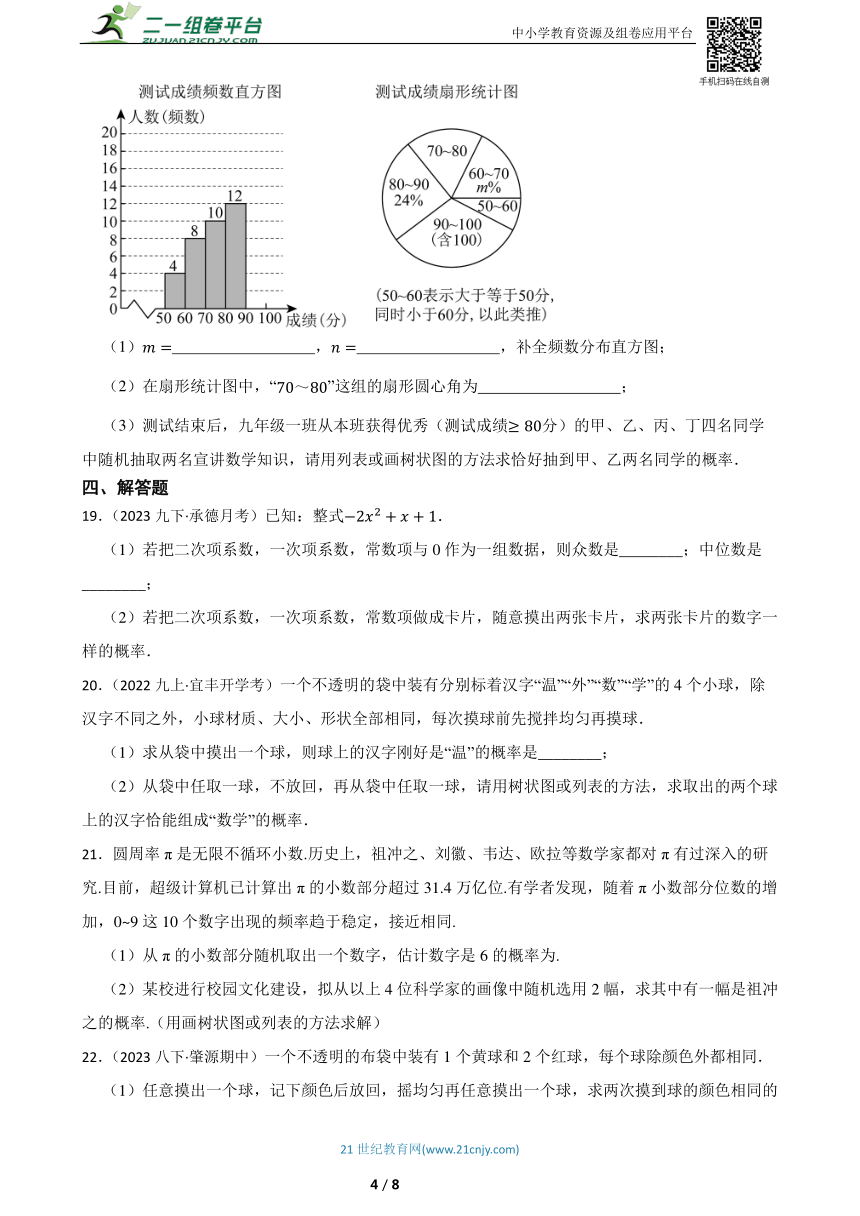
18.(2024九上·光明月考)月日被定为“国际数学日”,某校数学兴趣小组为调查学生对相关知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如下的频数分布直方图和扇形统计图.
(1) , ,补全频数分布直方图;
(2)在扇形统计图中,“”这组的扇形圆心角为 ;
(3)测试结束后,九年级一班从本班获得优秀(测试成绩分)的甲、乙、丙、丁四名同学中随机抽取两名宣讲数学知识,请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.
四、解答题
19.(2023九下·承德月考)已知:整式.
(1)若把二次项系数,一次项系数,常数项与0作为一组数据,则众数是________;中位数是________;
(2)若把二次项系数,一次项系数,常数项做成卡片,随意摸出两张卡片,求两张卡片的数字一样的概率.
20.(2022九上·宜丰开学考)一个不透明的袋中装有分别标着汉字“温”“外”“数”“学”的4个小球,除汉字不同之外,小球材质、大小、形状全部相同,每次摸球前先搅拌均匀再摸球.
(1)求从袋中摸出一个球,则球上的汉字刚好是“温”的概率是________;
(2)从袋中任取一球,不放回,再从袋中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字恰能组成“数学”的概率.
21.圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从π的小数部分随机取出一个数字,估计数字是6的概率为.
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表的方法求解)
22.(2023八下·肇源期中)一个不透明的布袋中装有1个黄球和2个红球,每个球除颜色外都相同.
(1)任意摸出一个球,记下颜色后放回,摇均匀再任意摸出一个球,求两次摸到球的颜色相同的概率;
(2)现将n个蓝球放入布袋,搅匀后任意摸出一个球,记录其颜色后放回,重复该实验.经过大量实验后,发现摸到蓝球的频率稳定于0.7附近,求n的值.
答案解析部分
1.【答案】C
【知识点】用列表法或树状图法求概率
2.【答案】C
【知识点】概率的意义
3.【答案】C
【知识点】概率公式
4.【答案】B
【知识点】概率公式;简单事件概率的计算
5.【答案】C
【知识点】用列表法或树状图法求概率
6.【答案】B
【知识点】用列表法或树状图法求概率
7.【答案】A
【知识点】用列表法或树状图法求概率
8.【答案】B
【知识点】概率公式
9.【答案】A
【知识点】概率公式
10.【答案】C
【知识点】复合事件概率的计算
11.【答案】
【知识点】等可能事件的概率
12.【答案】
【知识点】用列表法或树状图法求概率
13.【答案】6
【知识点】简单事件概率的计算
14.【答案】
【知识点】用列表法或树状图法求概率;复合事件概率的计算
15.【答案】
【知识点】几何概率
16.【答案】
【知识点】解分式方程;分式方程的增根;简单事件概率的计算
17.【答案】(1)0.25;(2).
【知识点】用列表法或树状图法求概率
18.【答案】(1),,
补全频数分布直方图如图所示,
(2);
(3)解:画树状图如下:
共有种等可能的结果,其中恰好抽到甲、乙两名同学的结果有:甲乙、乙甲,共种,
∴恰好抽到甲、乙两名同学的概率为.
【知识点】频数(率)分布直方图;扇形统计图;用列表法或树状图法求概率
19.【答案】(1)1;
(2)
【知识点】用列表法或树状图法求概率;多项式的项、系数与次数;中位数;众数
20.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)解:∵随着π小数部分位数的增加,0~9这10个数 字出现的频率趋于稳定,
∴从π的小数部分随机取出一个数字共有10 种等可能结果,其中出现数字6的只有1种结果,
∴从π的小数部分随机取出一个数字,估计是 数字6的概率为
(2)解:将祖冲之、刘徽、韦达、欧拉四位数学家分别记 作甲、乙、丙、丁,列表如下:
甲 乙 丙 丁
甲 — (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) — (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) — (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁) —
∵共有12种等可能的情况,其中有一幅是祖冲 之的有6种结果,
∴其中有一幅是祖冲之的概率为
【知识点】用列表法或树状图法求概率
22.【答案】(1))两次摸到球的颜色相同的概率为;(2)n=7.
【知识点】用列表法或树状图法求概率
21世纪教育网(www.21cnjy.com)
1 / 8
2.2 简单事件的概率
一、单选题
1.(2024九下·香坊模拟)小明、小红、小刚3位同学合影留念,3人随机站成一排,那么小明、小刚两人恰好相邻的概率是( ).
A. B. C. D.
2.(2020九上·广东期末)某地质学家预测:在未来的20年内,F市发生地震的概率是 .以下叙述正确的是( )
A.从现在起经过13至14年F市将会发生一次地震
B.可以确定F市在未来20年内将会发生一次地震
C.未来20年内,F市发生地震的可能性比没有发生地震的可能性大
D.我们不能判断未来会发生什么事,因此没有人可以确定何时会有地震发生
3.(2023九上·温州期中)现有三张正面分别印有2023年杭州亚运会吉祥物“琮琮”、“宸宸”和“莲莲”的不透明卡片,卡片除正面图案不同外,其余均相同.将三张卡片正面向下,从中随机抽取一张是“琮琮”的概率是( )
A. B. C. D.
4.(2024九上·宣汉期末)一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为( )
A. B. C. D.
5.(2024九上·顺德期中)用如图所示的两个可自由转动的转盘做“配紫色”游戏(红色和蓝色配成紫色),那么转盘停止时指针所指的颜色可配成紫色的概率是( )
A. B. C. D.
6.经过某十字路口的汽车,它可能继续直行,也可能向左或向右转.若这三种可能性相同,则甲、乙两辆汽车经过该十字路口都继续直行的概率为( )
A. B. C. D.
7.如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
A. B. C. D.
8.若一个不透明的袋子中装有2个白球、3个黄球和1个红球,这些球除颜色外其他完全相同,则从袋子中随机摸出一个球是白球的概率为( )
A. B. C. D.
9.(2019·三亚模拟)在1,2,3三个数中任取两个,组成一个两位数,则组成的两位数是偶数的概率为()
A. B. C. D.
10.(2023·永嘉模拟)甲乙丙丁四人互相给其他三人之一写信,选择对象的方式等可能.问存在两个人收到对方的信的概率( )
A. B. C. D.
二、填空题
11.(2018·天津)不透明袋子中装有11个球,其中有6个红球,3个黄球,2个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .
12.(2025·建始模拟)现有分别标有汉字“爱”“我”“中”“华”的四张卡片,它们除汉字外无其他差别.若把四张卡片背面朝上,洗匀放在桌子上,然后任意抽取一张卡片,不放回,再任意抽取一张,则两次抽取的卡片上的汉字能组成“中华”的概率是 .
13.(2024七下·东营期中)一个不透明的袋中装有除颜色外均相同的8个红球和m个黄球,从中随机摸出一个,摸到红球的概率为,则m= .
14.(2024九下·龙岗开学考) 我市在某展览馆举办美丽乡村成果展,该展览馆出入口示意图如图所示,小颖从A入口进E出口出来的概率是 .
15.(2024九上·昭阳期末)在边长为2的正方形中有一个最大的圆,向此正方形中任意丢一粒大米,“大米落在圆内”的概率为 .
16.(2024·内江模拟)取5张看上去无差别的卡片,分别在正面写上数字:,1,,2,,3,现把它们洗匀正面朝下,随机摆放在桌面上.从中任意抽出1张,记卡片上的数字为,则数字使分式方程无解的概率为 .
三、计算题
17.(2024九上·东阳期中)盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n 100 200 300 500 800 1000
摸到黑棋的次数m 24 51 76 124 201 250
摸到黑棋的频率(精确到0.001) 0.240 0.255 0.253 0.248 0.251 0.250
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
18.(2024九上·光明月考)月日被定为“国际数学日”,某校数学兴趣小组为调查学生对相关知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如下的频数分布直方图和扇形统计图.
(1) , ,补全频数分布直方图;
(2)在扇形统计图中,“”这组的扇形圆心角为 ;
(3)测试结束后,九年级一班从本班获得优秀(测试成绩分)的甲、乙、丙、丁四名同学中随机抽取两名宣讲数学知识,请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.
四、解答题
19.(2023九下·承德月考)已知:整式.
(1)若把二次项系数,一次项系数,常数项与0作为一组数据,则众数是________;中位数是________;
(2)若把二次项系数,一次项系数,常数项做成卡片,随意摸出两张卡片,求两张卡片的数字一样的概率.
20.(2022九上·宜丰开学考)一个不透明的袋中装有分别标着汉字“温”“外”“数”“学”的4个小球,除汉字不同之外,小球材质、大小、形状全部相同,每次摸球前先搅拌均匀再摸球.
(1)求从袋中摸出一个球,则球上的汉字刚好是“温”的概率是________;
(2)从袋中任取一球,不放回,再从袋中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字恰能组成“数学”的概率.
21.圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从π的小数部分随机取出一个数字,估计数字是6的概率为.
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表的方法求解)
22.(2023八下·肇源期中)一个不透明的布袋中装有1个黄球和2个红球,每个球除颜色外都相同.
(1)任意摸出一个球,记下颜色后放回,摇均匀再任意摸出一个球,求两次摸到球的颜色相同的概率;
(2)现将n个蓝球放入布袋,搅匀后任意摸出一个球,记录其颜色后放回,重复该实验.经过大量实验后,发现摸到蓝球的频率稳定于0.7附近,求n的值.
答案解析部分
1.【答案】C
【知识点】用列表法或树状图法求概率
2.【答案】C
【知识点】概率的意义
3.【答案】C
【知识点】概率公式
4.【答案】B
【知识点】概率公式;简单事件概率的计算
5.【答案】C
【知识点】用列表法或树状图法求概率
6.【答案】B
【知识点】用列表法或树状图法求概率
7.【答案】A
【知识点】用列表法或树状图法求概率
8.【答案】B
【知识点】概率公式
9.【答案】A
【知识点】概率公式
10.【答案】C
【知识点】复合事件概率的计算
11.【答案】
【知识点】等可能事件的概率
12.【答案】
【知识点】用列表法或树状图法求概率
13.【答案】6
【知识点】简单事件概率的计算
14.【答案】
【知识点】用列表法或树状图法求概率;复合事件概率的计算
15.【答案】
【知识点】几何概率
16.【答案】
【知识点】解分式方程;分式方程的增根;简单事件概率的计算
17.【答案】(1)0.25;(2).
【知识点】用列表法或树状图法求概率
18.【答案】(1),,
补全频数分布直方图如图所示,
(2);
(3)解:画树状图如下:
共有种等可能的结果,其中恰好抽到甲、乙两名同学的结果有:甲乙、乙甲,共种,
∴恰好抽到甲、乙两名同学的概率为.
【知识点】频数(率)分布直方图;扇形统计图;用列表法或树状图法求概率
19.【答案】(1)1;
(2)
【知识点】用列表法或树状图法求概率;多项式的项、系数与次数;中位数;众数
20.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)解:∵随着π小数部分位数的增加,0~9这10个数 字出现的频率趋于稳定,
∴从π的小数部分随机取出一个数字共有10 种等可能结果,其中出现数字6的只有1种结果,
∴从π的小数部分随机取出一个数字,估计是 数字6的概率为
(2)解:将祖冲之、刘徽、韦达、欧拉四位数学家分别记 作甲、乙、丙、丁,列表如下:
甲 乙 丙 丁
甲 — (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) — (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) — (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁) —
∵共有12种等可能的情况,其中有一幅是祖冲 之的有6种结果,
∴其中有一幅是祖冲之的概率为
【知识点】用列表法或树状图法求概率
22.【答案】(1))两次摸到球的颜色相同的概率为;(2)n=7.
【知识点】用列表法或树状图法求概率
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
