2.3 用频率估计概率 同步练习(含答案)
文档属性
| 名称 | 2.3 用频率估计概率 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 322.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:11:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.3 用频率估计概率
一、单选题
1.(2023九上·成都期末)在一个不透明的口袋中装有红球和白球共50个,这些球除颜色外其它完全相同,将口袋中的球搅匀后,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,通过大量重复摸球实验后,发现摸到白球的频率稳定在0.4,则口袋中白球的个数约为( )
A.25 B.20 C.30 D.35
2.为了了解某地区九年级男生的身高情况,随机抽取了该地区九年级100名男生的身高,统计如下:
组别(cm)
人数 5 38 42 15
据此,抽查该地区一名九年级男生,估计他的身高不低于180cm的概率是( ).
A.0.85 B.0.57 C.0.42 D.0.15
3.(2025九上·古丈期末)用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,那么掷一枚质地均匀的硬币10次,下列说法正确的是( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
4.(2025九下·深圳开学考)如图①所示,一张纸片上有一个不规则的图案(图中画图部分),小聪想了解该图案的面积是多少,他采取了以下的办法:用一个长为5m,宽为3m的长方形,将不规则图案围起来,然后在适当位置随机地向长方形区域扔小球,并记录小球在不规则图案上的次数(球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图②所示的折线统计图,由此他估计此不规则图案的面积大约为( )
A.6m2 B.5 m2 C.4m2 D.3m2
5.(2023九上·太谷期末)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),为了解该图案的面积是多少,小丽采取了以下办法:用一个面积为的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了如图②所示的统计图,由此估计不规则图案的面积大约为( )
A. B. C. D.
6.一个不透明的袋子中装有2个白球和若干个黑球,它们除颜色外完全相同,从袋子中随机摸出一球,记下颜色并放回,重复该实验多次,发现摸到白球的频率稳定在0.4,则可判断袋子中黑球的个数为( )
A.2个 B.3个 C.4个 D.5个
7.一只不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.如果想使摸到这三种颜色的球的概率相等,下列做法正确的是( )
A.向袋子里分别投放1个白球,1个黄球,1个红球
B.向袋子里分别投放3个白球,2个黄球,1个红球
C.向袋子里分别投放2个白球,1个红球
D.向袋子里投放2个白球
8.(2024九上·佛山期中)把个除颜色外完全相同的小球,放在一个不透明的盒子中. 其中有个白球.做大量重复试验:每次将球充分搅匀后,任意摸出个球记下颜色再放回盒子. 最终发现摸到白球的频率稳定在左右,则的值大约为( )
A. B. C. D.
9.(2024九下·重庆市模拟)从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中白球的个数约为( )
A.10 B.15 C.20 D.30
二、填空题
10.(2022·市南区模拟)林业部门要观察某种树苗在一定条件下的移植成活率,下表是这种树苗在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 853 1356 2220 3500 7056 13170 17580 26400
成活的频率 0.853 0.904 0.888 0.875 0.882 0.878 0.879 0.880
根据以上数据,该林业部门估计在此条件下移植的55000棵树苗成活的棵数约为 .
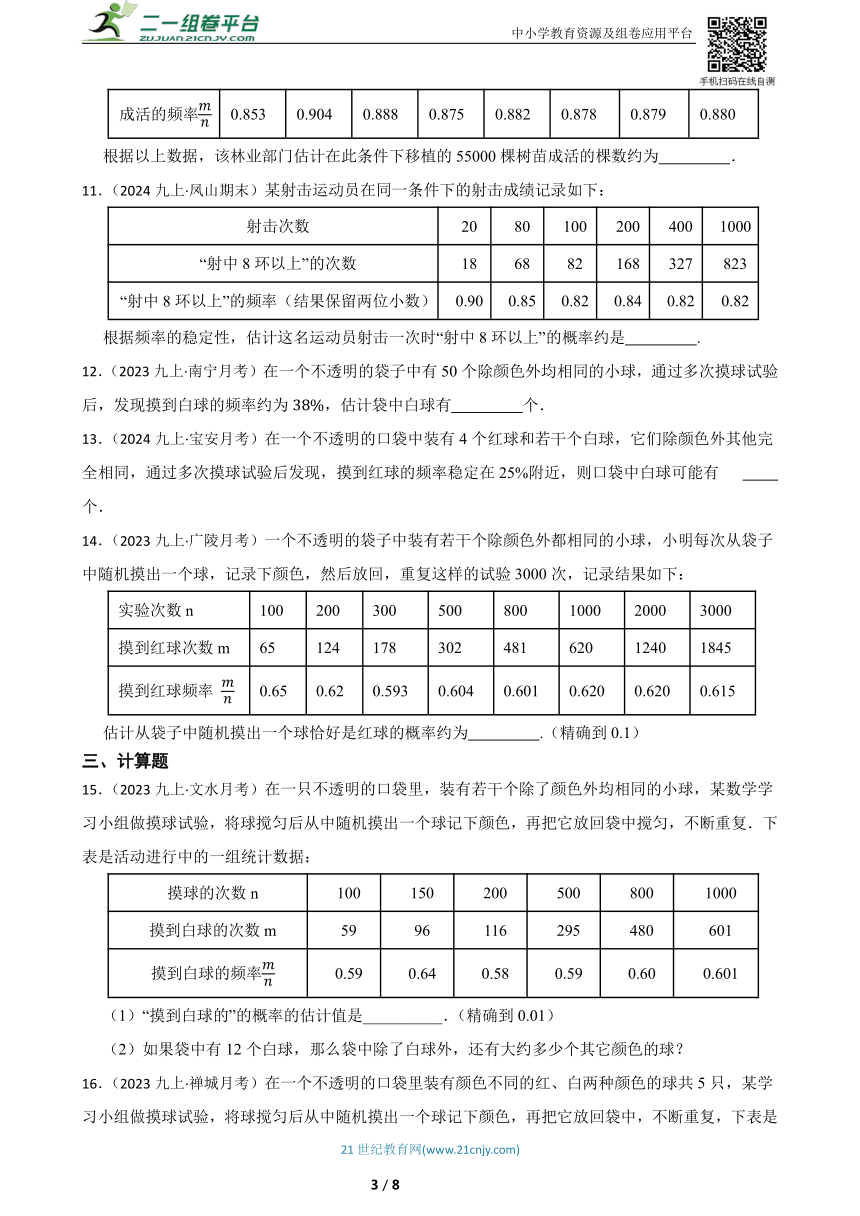
11.(2024九上·凤山期末)某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中8环以上”的次数 18 68 82 168 327 823
“射中8环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中8环以上”的概率约是 .
12.(2023九上·南宁月考)在一个不透明的袋子中有50个除颜色外均相同的小球,通过多次摸球试验后,发现摸到白球的频率约为,估计袋中白球有 个.
13.(2024九上·宝安月考)在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 个.
14.(2023九上·广陵月考)一个不透明的袋子中装有若干个除颜色外都相同的小球,小明每次从袋子中随机摸出一个球,记录下颜色,然后放回,重复这样的试验3000次,记录结果如下:
实验次数n 100 200 300 500 800 1000 2000 3000
摸到红球次数m 65 124 178 302 481 620 1240 1845
摸到红球频率 0.65 0.62 0.593 0.604 0.601 0.620 0.620 0.615
估计从袋子中随机摸出一个球恰好是红球的概率约为 .(精确到0.1)
三、计算题
15.(2023九上·文水月考)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中搅匀,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 295 480 601
摸到白球的频率 0.59 0.64 0.58 0.59 0.60 0.601
(1)“摸到白球的”的概率的估计值是__________.(精确到0.01)
(2)如果袋中有12个白球,那么袋中除了白球外,还有大约多少个其它颜色的球?
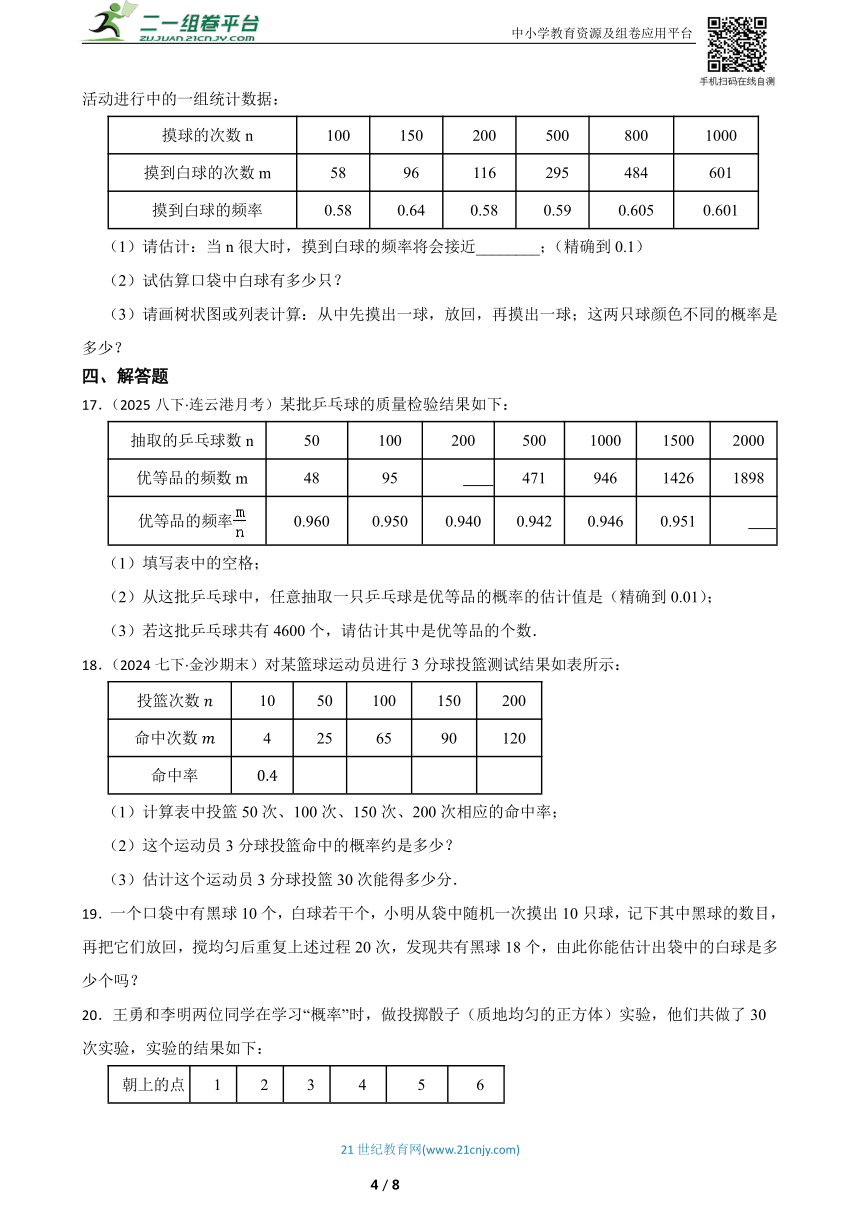
16.(2023九上·禅城月考)在一个不透明的口袋里装有颜色不同的红、白两种颜色的球共5只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近________;(精确到0.1)
(2)试估算口袋中白球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,放回,再摸出一球;这两只球颜色不同的概率是多少?
四、解答题
17.(2025八下·连云港月考)某批乒乓球的质量检验结果如下:
抽取的乒乓球数n 50 100 200 500 1000 1500 2000
优等品的频数m 48 95 471 946 1426 1898
优等品的频率 0.960 0.950 0.940 0.942 0.946 0.951
(1)填写表中的空格;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是(精确到0.01);
(3)若这批乒乓球共有4600个,请估计其中是优等品的个数.
18.(2024七下·金沙期末)对某篮球运动员进行3分球投篮测试结果如表所示:
投篮次数 10 50 100 150 200
命中次数 4 25 65 90 120
命中率
(1)计算表中投篮50次、100次、150次、200次相应的命中率;
(2)这个运动员3分球投篮命中的概率约是多少?
(3)估计这个运动员3分球投篮30次能得多少分.
19.一个口袋中有黑球10个,白球若干个,小明从袋中随机一次摸出10只球,记下其中黑球的数目,再把它们放回,搅均匀后重复上述过程20次,发现共有黑球18个,由此你能估计出袋中的白球是多少个吗?
20.王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 2 5 6 4 10 3
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
答案解析部分
1.【答案】B
【知识点】利用频率估计概率
2.【答案】D
【知识点】利用频率估计概率
3.【答案】B
【知识点】利用频率估计概率
4.【答案】A
【知识点】利用频率估计概率
5.【答案】B
【知识点】几何概率;利用频率估计概率
6.【答案】B
【知识点】利用频率估计概率
7.【答案】B
【知识点】模拟实验
8.【答案】A
【知识点】利用频率估计概率;简单事件概率的计算
9.【答案】C
【知识点】利用频率估计概率
10.【答案】48400
【知识点】利用频率估计概率
11.【答案】0.82
【知识点】利用频率估计概率
12.【答案】
【知识点】利用频率估计概率;简单事件概率的计算
13.【答案】12
【知识点】利用频率估计概率
14.【答案】0.6
【知识点】利用频率估计概率
15.【答案】(1)
(2)个
【知识点】利用频率估计概率;简单事件概率的计算
16.【答案】(1)0.6
(2)3只
(3)
【知识点】用列表法或树状图法求概率;利用频率估计概率;简单事件概率的计算
17.【答案】(1)188,0.949;(2)0.95;(3)4370
【知识点】利用频率估计概率
18.【答案】(1)解:投篮50次、100次、150次、200次相应的命中率分别为:
;;;;
(2)解:由表格数据知,当投篮次数逐渐增加时,命中率稳定在0.6附近,所以估计这个运动员3分球投篮0.6;
(3)解:由(2)的结论可知这个运动员投篮30次,命中的次数约为(次),约能得到(分).
【知识点】利用频率估计概率;简单事件概率的计算
19.【答案】解:黑球概率近似等于频率,设白球有m个,则解得m=101.11
故袋中的白球大约有101个.
【知识点】利用频率估计概率
20.【答案】解:(1)“3点朝上”的频率为:,
“5点朝上”的频率为:;
(2)王勇的说法是错误的
因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大,
只有当实验次数足够大时,该事件发生的频率才能稳定在事件发生的概率附近,也才能用该事件发生的频率区估计其概率.
李明的说法也是错误的,因为事件的发生具有随机性,所以投掷300次,出现“6点朝上”的次数不一定是30次.
(3)列表:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
∵朝上的点数之和为3的倍数共有12个,
∴P(点数之和为3的倍数)= .
【知识点】利用频率估计概率
21世纪教育网(www.21cnjy.com)
8 / 8
2.3 用频率估计概率
一、单选题
1.(2023九上·成都期末)在一个不透明的口袋中装有红球和白球共50个,这些球除颜色外其它完全相同,将口袋中的球搅匀后,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,通过大量重复摸球实验后,发现摸到白球的频率稳定在0.4,则口袋中白球的个数约为( )
A.25 B.20 C.30 D.35
2.为了了解某地区九年级男生的身高情况,随机抽取了该地区九年级100名男生的身高,统计如下:
组别(cm)
人数 5 38 42 15
据此,抽查该地区一名九年级男生,估计他的身高不低于180cm的概率是( ).
A.0.85 B.0.57 C.0.42 D.0.15
3.(2025九上·古丈期末)用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,那么掷一枚质地均匀的硬币10次,下列说法正确的是( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
4.(2025九下·深圳开学考)如图①所示,一张纸片上有一个不规则的图案(图中画图部分),小聪想了解该图案的面积是多少,他采取了以下的办法:用一个长为5m,宽为3m的长方形,将不规则图案围起来,然后在适当位置随机地向长方形区域扔小球,并记录小球在不规则图案上的次数(球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图②所示的折线统计图,由此他估计此不规则图案的面积大约为( )
A.6m2 B.5 m2 C.4m2 D.3m2
5.(2023九上·太谷期末)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),为了解该图案的面积是多少,小丽采取了以下办法:用一个面积为的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了如图②所示的统计图,由此估计不规则图案的面积大约为( )
A. B. C. D.
6.一个不透明的袋子中装有2个白球和若干个黑球,它们除颜色外完全相同,从袋子中随机摸出一球,记下颜色并放回,重复该实验多次,发现摸到白球的频率稳定在0.4,则可判断袋子中黑球的个数为( )
A.2个 B.3个 C.4个 D.5个
7.一只不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.如果想使摸到这三种颜色的球的概率相等,下列做法正确的是( )
A.向袋子里分别投放1个白球,1个黄球,1个红球
B.向袋子里分别投放3个白球,2个黄球,1个红球
C.向袋子里分别投放2个白球,1个红球
D.向袋子里投放2个白球
8.(2024九上·佛山期中)把个除颜色外完全相同的小球,放在一个不透明的盒子中. 其中有个白球.做大量重复试验:每次将球充分搅匀后,任意摸出个球记下颜色再放回盒子. 最终发现摸到白球的频率稳定在左右,则的值大约为( )
A. B. C. D.
9.(2024九下·重庆市模拟)从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中白球的个数约为( )
A.10 B.15 C.20 D.30
二、填空题
10.(2022·市南区模拟)林业部门要观察某种树苗在一定条件下的移植成活率,下表是这种树苗在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 853 1356 2220 3500 7056 13170 17580 26400
成活的频率 0.853 0.904 0.888 0.875 0.882 0.878 0.879 0.880
根据以上数据,该林业部门估计在此条件下移植的55000棵树苗成活的棵数约为 .
11.(2024九上·凤山期末)某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中8环以上”的次数 18 68 82 168 327 823
“射中8环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中8环以上”的概率约是 .
12.(2023九上·南宁月考)在一个不透明的袋子中有50个除颜色外均相同的小球,通过多次摸球试验后,发现摸到白球的频率约为,估计袋中白球有 个.
13.(2024九上·宝安月考)在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 个.
14.(2023九上·广陵月考)一个不透明的袋子中装有若干个除颜色外都相同的小球,小明每次从袋子中随机摸出一个球,记录下颜色,然后放回,重复这样的试验3000次,记录结果如下:
实验次数n 100 200 300 500 800 1000 2000 3000
摸到红球次数m 65 124 178 302 481 620 1240 1845
摸到红球频率 0.65 0.62 0.593 0.604 0.601 0.620 0.620 0.615
估计从袋子中随机摸出一个球恰好是红球的概率约为 .(精确到0.1)
三、计算题
15.(2023九上·文水月考)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中搅匀,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 295 480 601
摸到白球的频率 0.59 0.64 0.58 0.59 0.60 0.601
(1)“摸到白球的”的概率的估计值是__________.(精确到0.01)
(2)如果袋中有12个白球,那么袋中除了白球外,还有大约多少个其它颜色的球?
16.(2023九上·禅城月考)在一个不透明的口袋里装有颜色不同的红、白两种颜色的球共5只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近________;(精确到0.1)
(2)试估算口袋中白球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,放回,再摸出一球;这两只球颜色不同的概率是多少?
四、解答题
17.(2025八下·连云港月考)某批乒乓球的质量检验结果如下:
抽取的乒乓球数n 50 100 200 500 1000 1500 2000
优等品的频数m 48 95 471 946 1426 1898
优等品的频率 0.960 0.950 0.940 0.942 0.946 0.951
(1)填写表中的空格;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是(精确到0.01);
(3)若这批乒乓球共有4600个,请估计其中是优等品的个数.
18.(2024七下·金沙期末)对某篮球运动员进行3分球投篮测试结果如表所示:
投篮次数 10 50 100 150 200
命中次数 4 25 65 90 120
命中率
(1)计算表中投篮50次、100次、150次、200次相应的命中率;
(2)这个运动员3分球投篮命中的概率约是多少?
(3)估计这个运动员3分球投篮30次能得多少分.
19.一个口袋中有黑球10个,白球若干个,小明从袋中随机一次摸出10只球,记下其中黑球的数目,再把它们放回,搅均匀后重复上述过程20次,发现共有黑球18个,由此你能估计出袋中的白球是多少个吗?
20.王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 2 5 6 4 10 3
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
答案解析部分
1.【答案】B
【知识点】利用频率估计概率
2.【答案】D
【知识点】利用频率估计概率
3.【答案】B
【知识点】利用频率估计概率
4.【答案】A
【知识点】利用频率估计概率
5.【答案】B
【知识点】几何概率;利用频率估计概率
6.【答案】B
【知识点】利用频率估计概率
7.【答案】B
【知识点】模拟实验
8.【答案】A
【知识点】利用频率估计概率;简单事件概率的计算
9.【答案】C
【知识点】利用频率估计概率
10.【答案】48400
【知识点】利用频率估计概率
11.【答案】0.82
【知识点】利用频率估计概率
12.【答案】
【知识点】利用频率估计概率;简单事件概率的计算
13.【答案】12
【知识点】利用频率估计概率
14.【答案】0.6
【知识点】利用频率估计概率
15.【答案】(1)
(2)个
【知识点】利用频率估计概率;简单事件概率的计算
16.【答案】(1)0.6
(2)3只
(3)
【知识点】用列表法或树状图法求概率;利用频率估计概率;简单事件概率的计算
17.【答案】(1)188,0.949;(2)0.95;(3)4370
【知识点】利用频率估计概率
18.【答案】(1)解:投篮50次、100次、150次、200次相应的命中率分别为:
;;;;
(2)解:由表格数据知,当投篮次数逐渐增加时,命中率稳定在0.6附近,所以估计这个运动员3分球投篮0.6;
(3)解:由(2)的结论可知这个运动员投篮30次,命中的次数约为(次),约能得到(分).
【知识点】利用频率估计概率;简单事件概率的计算
19.【答案】解:黑球概率近似等于频率,设白球有m个,则解得m=101.11
故袋中的白球大约有101个.
【知识点】利用频率估计概率
20.【答案】解:(1)“3点朝上”的频率为:,
“5点朝上”的频率为:;
(2)王勇的说法是错误的
因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大,
只有当实验次数足够大时,该事件发生的频率才能稳定在事件发生的概率附近,也才能用该事件发生的频率区估计其概率.
李明的说法也是错误的,因为事件的发生具有随机性,所以投掷300次,出现“6点朝上”的次数不一定是30次.
(3)列表:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
∵朝上的点数之和为3的倍数共有12个,
∴P(点数之和为3的倍数)= .
【知识点】利用频率估计概率
21世纪教育网(www.21cnjy.com)
8 / 8
同课章节目录
