3.3 垂径定理 同步练习(含答案)
文档属性
| 名称 | 3.3 垂径定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 528.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:13:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.3 垂径定理
一、单选题
1.(2023九上·文水期中)如图,的半径为5,于点C,若,则弦的长为( )
A.2 B.4 C.6 D.8
2.(2025九上·嘉兴期末)沈括在《梦溪笔谈》中收录了计算圆弧长度的“会圆术”,主要思路是局部以直代曲,进行近似计算.如图,是以为圆心、为半径的圆弧,是弦的中点,是的中点,则长度的近似值.若,,则( )
A. B. C. D.
3.(2024九上·合江期中)如图,在中,,,,以点C为圆心,长为半径的圆与交于点D,则的长为( )
A. B. C. D.
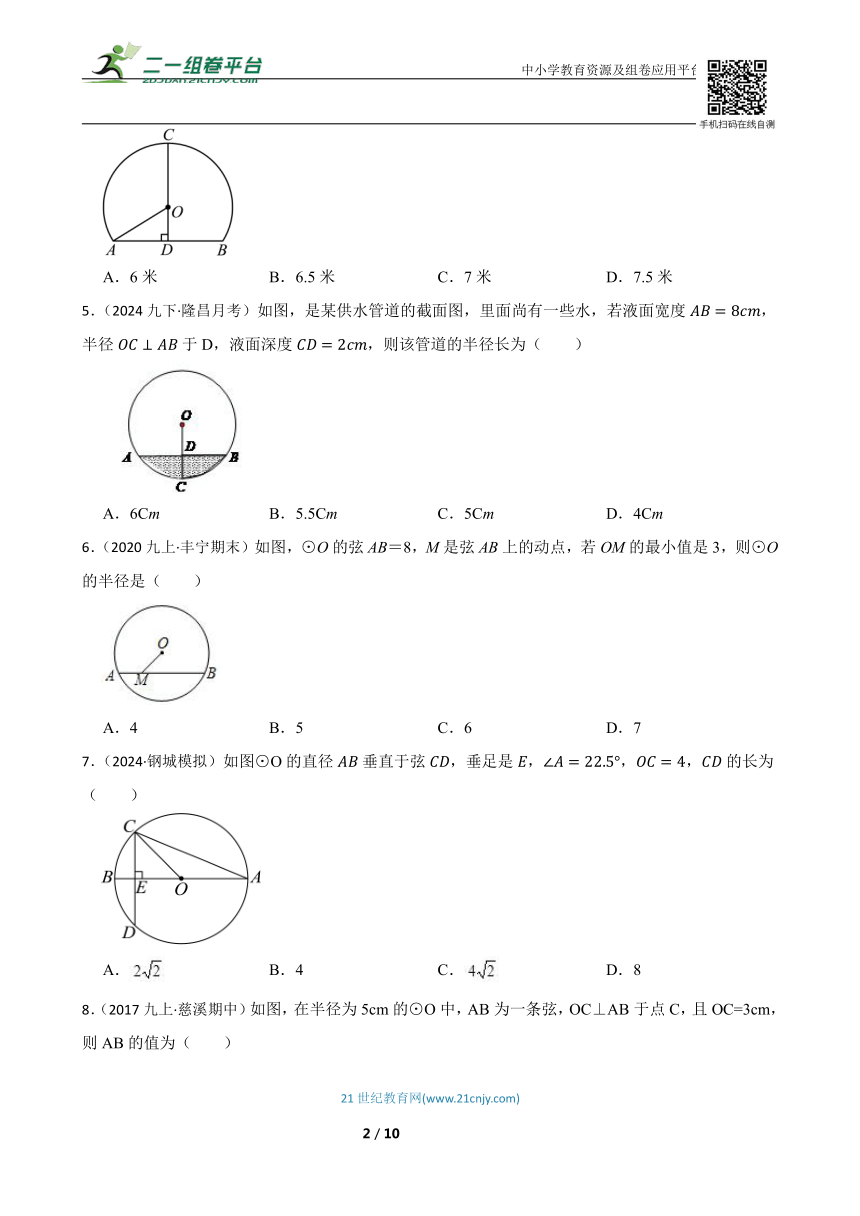
4.(2023九上·黄梅月考)黄冈市政府网消息,全长109公里的黄黄高速将进行改扩建,按双向八车道设计,高速公路的隧道和桥梁很多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面米,净高米,则此圆的半径( )
A.6米 B.6.5米 C.7米 D.7.5米
5.(2024九下·隆昌月考)如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于D,液面深度,则该管道的半径长为( )
A.6Cm B.5.5Cm C.5Cm D.4Cm
6.(2020九上·丰宁期末)如图,⊙O的弦AB=8,M是弦AB上的动点,若OM的最小值是3,则⊙O的半径是( )
A.4 B.5 C.6 D.7
7.(2024·钢城模拟)如图⊙O的直径垂直于弦,垂足是,,,的长为( )
A. B.4 C. D.8
8.(2017九上·慈溪期中)如图,在半径为5cm的⊙O中,AB为一条弦,OC⊥AB于点C,且OC=3cm,则AB的值为( )
A.3cm B.4cm C.6cm D.8cm
9.(2018九上·天台月考)如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE=( ).
A.8cm B.5cm C.3cm D.2cm
10.(2023九上·巴东月考)如图,在平面直角坐标系中,⊙O经过点(0,10),直线y=kx+2k﹣4与⊙O交于B、C两点,则弦BC的最小值是( )
A. B. C. D.以上都不对
二、填空题
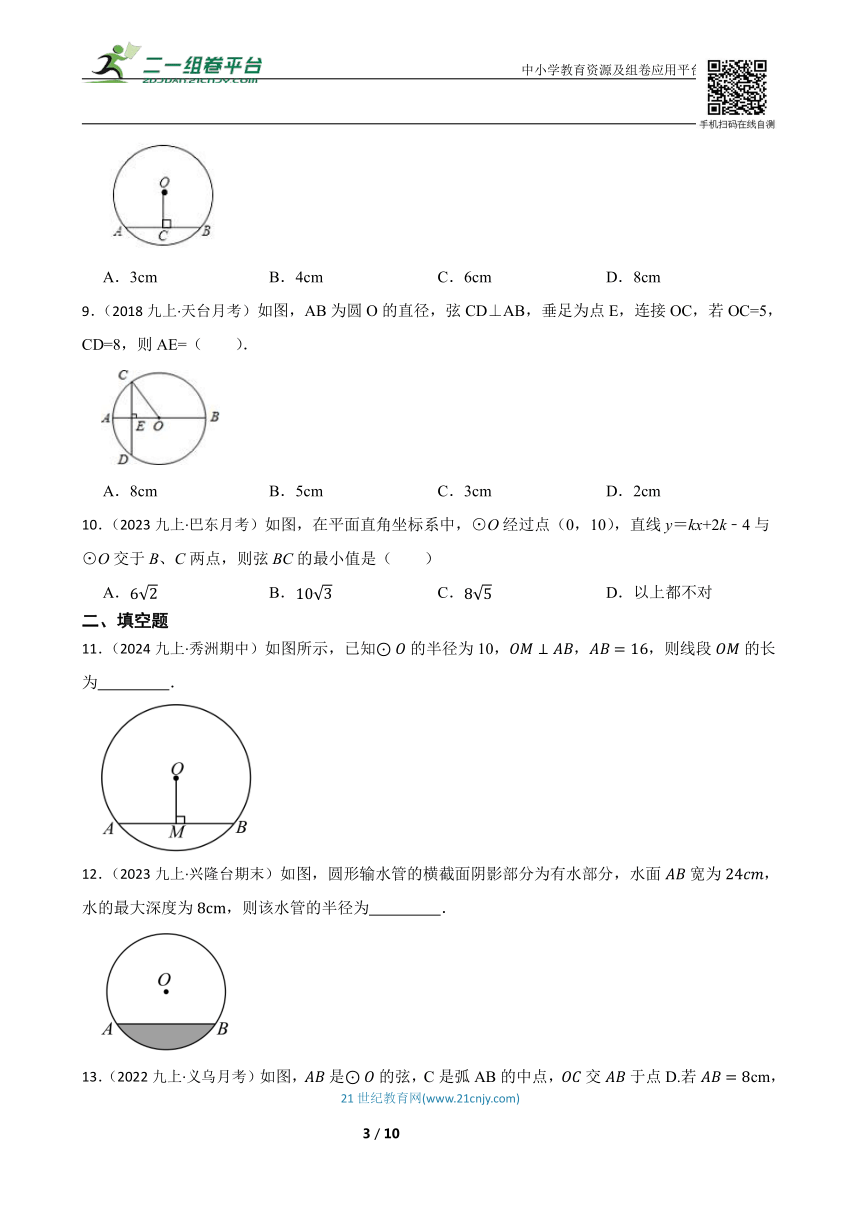
11.(2024九上·秀洲期中)如图所示,已知的半径为10,,,则线段的长为 .
12.(2023九上·兴隆台期末)如图,圆形输水管的横截面阴影部分为有水部分,水面宽为,水的最大深度为,则该水管的半径为 .
13.(2022九上·义乌月考)如图,是的弦,C是弧AB的中点,交于点D.若cm, cm,则的半径为 cm.
14.一根排水管的截面如图所示,已知排水管的半径OB=5cm,水面宽AB=8cm,则截面圆心O到水面的距离OC的长是 .
15.(2024九上·大安期末) 如图,某地新建一座石拱桥,桥拱是圆弧形,它的跨度AB为60m, 拱高CD为10m, 则桥拱所在圆的半径长为
16.(2025·旺苍模拟)如图,M为x轴正半轴上一点,与x轴负半轴交于点A,与y轴正半轴交于点B,连接,将绕顶点B逆时针旋转得到,此时点C恰在上,若半径为4,则点D的坐标是 .
三、计算题
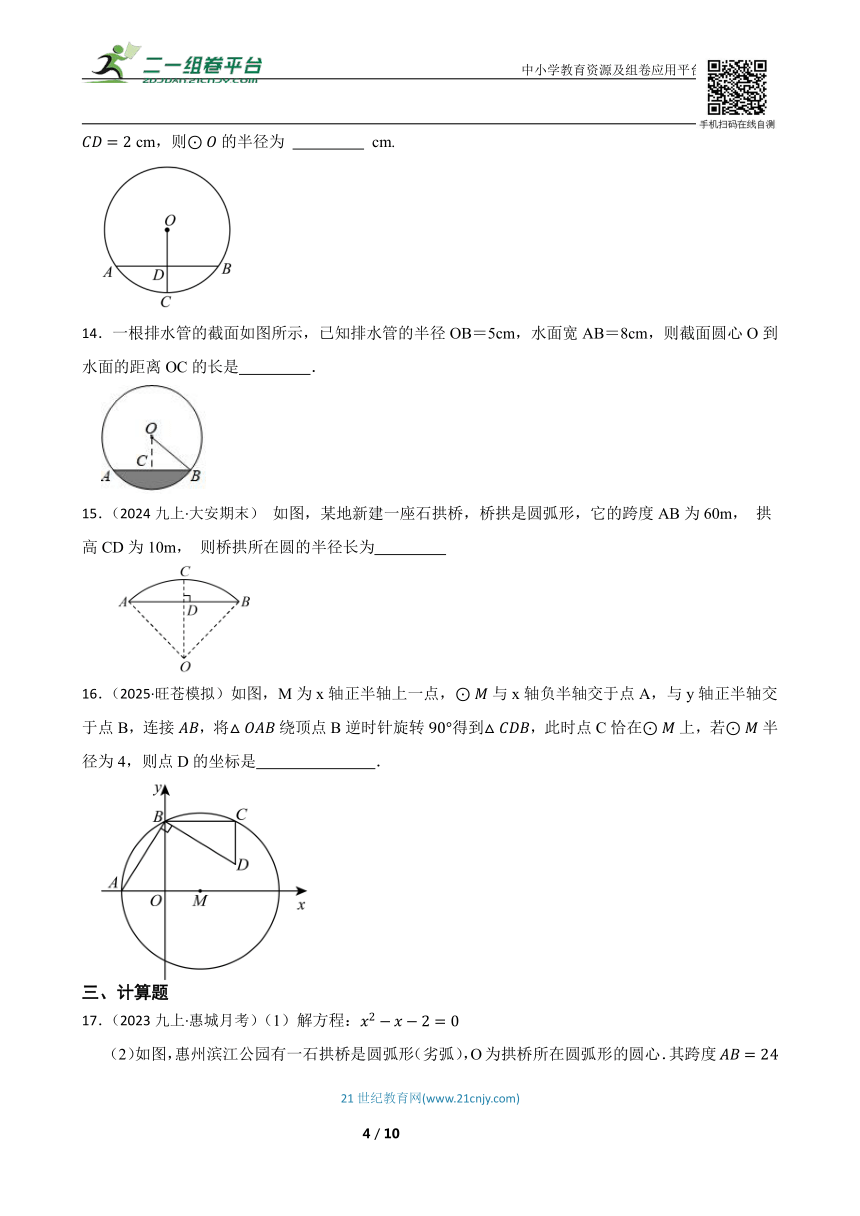
17.(2023九上·惠城月考)(1)解方程:
(2)如图,惠州滨江公园有一石拱桥是圆弧形(劣弧),O为拱桥所在圆弧形的圆心.其跨度米,拱高为8米,求圆弧所在的圆的半径.
18.(2021九上·江干月考)如图是一名考古学家发现的一块古代车轮碎片.
(1)请你帮他找到这个车轮的圆心(保留作图痕迹);
(2)若这个圆的半径为10cm,请求出弦心距为5cm的弦长.
四、解答题
19.(2024九上·北京市期中)如图,水平放置的一条油管的截面半径为,其中有油部分油面宽为,于点C,求截面上有油部分油面的高.
20.(2025九上·斗门期末)如图,直径为的圆柱形的油槽内装入一些油以后截面如图所示,若油面宽,求油的最大深度.
21.(2023九上·青龙期中)如图, 为圆 的直径,弦 于点 , , ,求圆 的半径.
22.(2024·南京会考)已知圆E的半径为2,,,A,T分别为,中点,求:
(1);
(2).
答案解析部分
1.【答案】D
【知识点】勾股定理;垂径定理
2.【答案】A
【知识点】勾股定理;垂径定理
3.【答案】C
【知识点】勾股定理;垂径定理
4.【答案】B
【知识点】勾股定理;垂径定理的实际应用
5.【答案】C
【知识点】垂径定理的实际应用
6.【答案】B
【知识点】勾股定理;垂径定理
7.【答案】C
【知识点】勾股定理;垂径定理
8.【答案】D
【知识点】垂径定理
9.【答案】D
【知识点】垂径定理
10.【答案】C
【知识点】垂径定理;一次函数的实际应用-几何问题
11.【答案】6
【知识点】勾股定理;垂径定理
12.【答案】
【知识点】勾股定理;垂径定理的实际应用
13.【答案】5
【知识点】勾股定理;垂径定理
14.【答案】3cm
【知识点】勾股定理;垂径定理
15.【答案】50
【知识点】垂径定理的实际应用
16.【答案】
【知识点】勾股定理;矩形的判定与性质;垂径定理;旋转的性质
17.【答案】(1),
(2)13米
【知识点】因式分解法解一元二次方程;勾股定理;垂径定理的实际应用
18.【答案】(1)解:作出圆的两条弦的垂直平分线的交点 ,
如图所示:
(2)解:由题意得下图:
其中 ,
在 中根据勾股定理得;
,
圆的半径为10cm,弦心距为5cm的弦长为: cm.
【知识点】勾股定理;垂径定理;尺规作图-垂直平分线
19.【答案】截面上有油部分油面的高为
【知识点】勾股定理;垂径定理
20.【答案】
【知识点】垂径定理的实际应用
21.【答案】解:
如图所示,连接OA,
∵CD是⊙O的直径,AB⊥CD
∴AE=BE
∵AB=6
∴AE=3
设OA=R
∴OE=R-1
根据勾股定理:R2=32+(R-1)2
解得R=5cm.
答:圆 的半径为5cm
【知识点】勾股定理;垂径定理
22.【答案】(1)
(2)
【知识点】三角形三边关系;垂径定理;直角三角形斜边上的中线
21世纪教育网(www.21cnjy.com)
3 / 10
3.3 垂径定理
一、单选题
1.(2023九上·文水期中)如图,的半径为5,于点C,若,则弦的长为( )
A.2 B.4 C.6 D.8
2.(2025九上·嘉兴期末)沈括在《梦溪笔谈》中收录了计算圆弧长度的“会圆术”,主要思路是局部以直代曲,进行近似计算.如图,是以为圆心、为半径的圆弧,是弦的中点,是的中点,则长度的近似值.若,,则( )
A. B. C. D.
3.(2024九上·合江期中)如图,在中,,,,以点C为圆心,长为半径的圆与交于点D,则的长为( )
A. B. C. D.
4.(2023九上·黄梅月考)黄冈市政府网消息,全长109公里的黄黄高速将进行改扩建,按双向八车道设计,高速公路的隧道和桥梁很多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面米,净高米,则此圆的半径( )
A.6米 B.6.5米 C.7米 D.7.5米
5.(2024九下·隆昌月考)如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于D,液面深度,则该管道的半径长为( )
A.6Cm B.5.5Cm C.5Cm D.4Cm
6.(2020九上·丰宁期末)如图,⊙O的弦AB=8,M是弦AB上的动点,若OM的最小值是3,则⊙O的半径是( )
A.4 B.5 C.6 D.7
7.(2024·钢城模拟)如图⊙O的直径垂直于弦,垂足是,,,的长为( )
A. B.4 C. D.8
8.(2017九上·慈溪期中)如图,在半径为5cm的⊙O中,AB为一条弦,OC⊥AB于点C,且OC=3cm,则AB的值为( )
A.3cm B.4cm C.6cm D.8cm
9.(2018九上·天台月考)如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE=( ).
A.8cm B.5cm C.3cm D.2cm
10.(2023九上·巴东月考)如图,在平面直角坐标系中,⊙O经过点(0,10),直线y=kx+2k﹣4与⊙O交于B、C两点,则弦BC的最小值是( )
A. B. C. D.以上都不对
二、填空题
11.(2024九上·秀洲期中)如图所示,已知的半径为10,,,则线段的长为 .
12.(2023九上·兴隆台期末)如图,圆形输水管的横截面阴影部分为有水部分,水面宽为,水的最大深度为,则该水管的半径为 .
13.(2022九上·义乌月考)如图,是的弦,C是弧AB的中点,交于点D.若cm, cm,则的半径为 cm.
14.一根排水管的截面如图所示,已知排水管的半径OB=5cm,水面宽AB=8cm,则截面圆心O到水面的距离OC的长是 .
15.(2024九上·大安期末) 如图,某地新建一座石拱桥,桥拱是圆弧形,它的跨度AB为60m, 拱高CD为10m, 则桥拱所在圆的半径长为
16.(2025·旺苍模拟)如图,M为x轴正半轴上一点,与x轴负半轴交于点A,与y轴正半轴交于点B,连接,将绕顶点B逆时针旋转得到,此时点C恰在上,若半径为4,则点D的坐标是 .
三、计算题
17.(2023九上·惠城月考)(1)解方程:
(2)如图,惠州滨江公园有一石拱桥是圆弧形(劣弧),O为拱桥所在圆弧形的圆心.其跨度米,拱高为8米,求圆弧所在的圆的半径.
18.(2021九上·江干月考)如图是一名考古学家发现的一块古代车轮碎片.
(1)请你帮他找到这个车轮的圆心(保留作图痕迹);
(2)若这个圆的半径为10cm,请求出弦心距为5cm的弦长.
四、解答题
19.(2024九上·北京市期中)如图,水平放置的一条油管的截面半径为,其中有油部分油面宽为,于点C,求截面上有油部分油面的高.
20.(2025九上·斗门期末)如图,直径为的圆柱形的油槽内装入一些油以后截面如图所示,若油面宽,求油的最大深度.
21.(2023九上·青龙期中)如图, 为圆 的直径,弦 于点 , , ,求圆 的半径.
22.(2024·南京会考)已知圆E的半径为2,,,A,T分别为,中点,求:
(1);
(2).
答案解析部分
1.【答案】D
【知识点】勾股定理;垂径定理
2.【答案】A
【知识点】勾股定理;垂径定理
3.【答案】C
【知识点】勾股定理;垂径定理
4.【答案】B
【知识点】勾股定理;垂径定理的实际应用
5.【答案】C
【知识点】垂径定理的实际应用
6.【答案】B
【知识点】勾股定理;垂径定理
7.【答案】C
【知识点】勾股定理;垂径定理
8.【答案】D
【知识点】垂径定理
9.【答案】D
【知识点】垂径定理
10.【答案】C
【知识点】垂径定理;一次函数的实际应用-几何问题
11.【答案】6
【知识点】勾股定理;垂径定理
12.【答案】
【知识点】勾股定理;垂径定理的实际应用
13.【答案】5
【知识点】勾股定理;垂径定理
14.【答案】3cm
【知识点】勾股定理;垂径定理
15.【答案】50
【知识点】垂径定理的实际应用
16.【答案】
【知识点】勾股定理;矩形的判定与性质;垂径定理;旋转的性质
17.【答案】(1),
(2)13米
【知识点】因式分解法解一元二次方程;勾股定理;垂径定理的实际应用
18.【答案】(1)解:作出圆的两条弦的垂直平分线的交点 ,
如图所示:
(2)解:由题意得下图:
其中 ,
在 中根据勾股定理得;
,
圆的半径为10cm,弦心距为5cm的弦长为: cm.
【知识点】勾股定理;垂径定理;尺规作图-垂直平分线
19.【答案】截面上有油部分油面的高为
【知识点】勾股定理;垂径定理
20.【答案】
【知识点】垂径定理的实际应用
21.【答案】解:
如图所示,连接OA,
∵CD是⊙O的直径,AB⊥CD
∴AE=BE
∵AB=6
∴AE=3
设OA=R
∴OE=R-1
根据勾股定理:R2=32+(R-1)2
解得R=5cm.
答:圆 的半径为5cm
【知识点】勾股定理;垂径定理
22.【答案】(1)
(2)
【知识点】三角形三边关系;垂径定理;直角三角形斜边上的中线
21世纪教育网(www.21cnjy.com)
3 / 10
同课章节目录
