3.4圆心角 同步练习(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
3.4圆心角
一、单选题
1.(2020九上·净月期末)如图,在⊙O中, = ,∠A=40°,则∠B的度数是( )
A.60° B.40° C.50° D.70°
2.(2025九下·织金月考)将一把折扇展开,可抽象看成一个扇形.若该扇形的半径为3,弧长为,则这个扇形的圆心角的度数为( )
A. B. C. D.
3.(2023九上·肇源期中)下列说法正确的是( )
A.相等的圆心角所对的弧相等,所对的弦相等
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.等弧所对的圆心角相等,所对的弦相等
D.圆是轴对称图形,其对称轴是任意一条直径
4.(2024九上·许昌月考)如图,AB是⊙O的直径,C、D是⊙O上的两点,且点C为弧BAD的中点,连接CD、CB、OD,CD与AB交于点F.若∠AOD=100°,则∠ABC的度数为( )
A.15° B.20° C.25° D.30°
5.(2024九上·南京月考)一个扇形的半径为4,弧长为,其圆心角度数是( )
A. B. C. D.
6.(2018九上·宁波期中)下列四个命题中,正确的有( )
①三点确定一个圆 ②平分弦的直径平分弦所对的弧
③弦长相等,则弦所对的弦心距也相等 ④相等的弧所对的圆心角相等
A.4个 B.3个 C.2个 D.1个
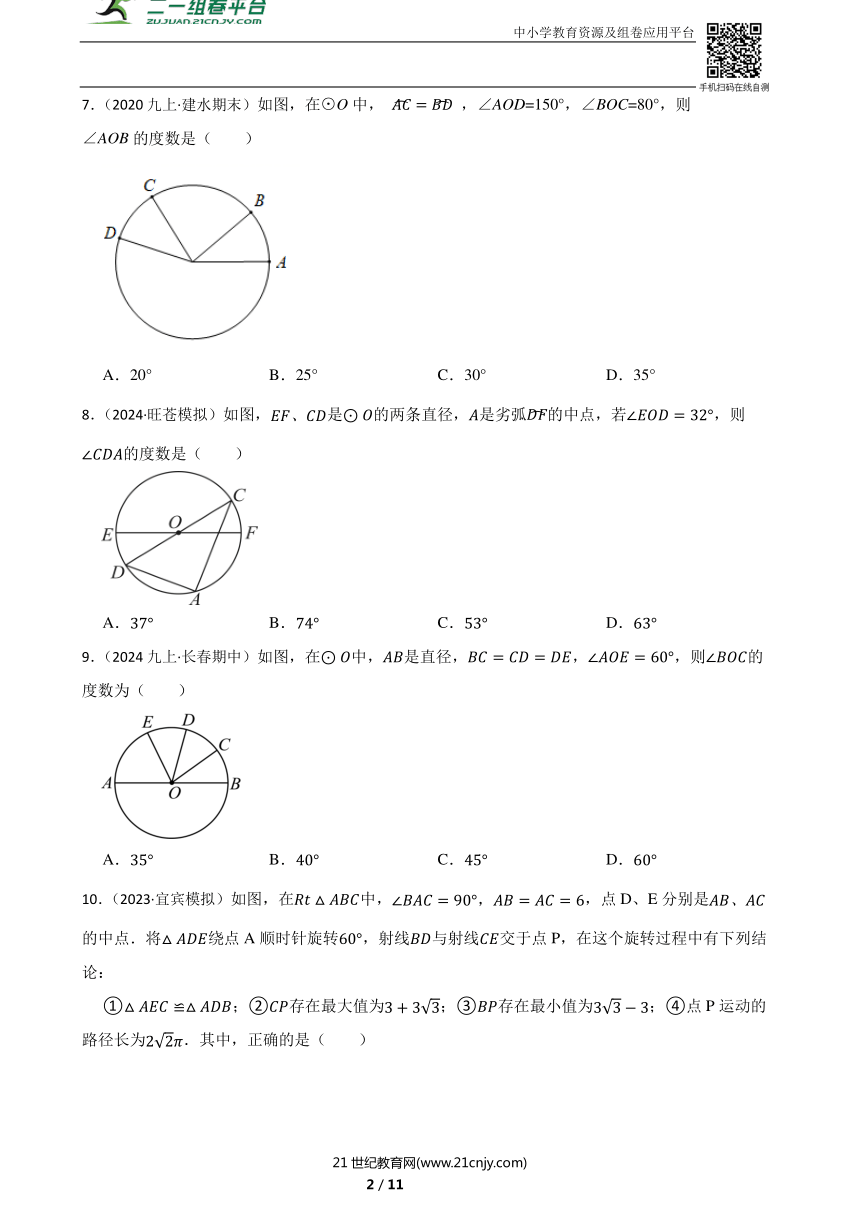
7.(2020九上·建水期末)如图,在⊙O中, ,∠AOD=150°,∠BOC=80°,则∠AOB的度数是( )
A.20° B.25° C.30° D.35°
8.(2024·旺苍模拟)如图,是的两条直径,是劣弧的中点,若,则的度数是( )
A. B. C. D.
9.(2024九上·长春期中)如图,在中,是直径,,,则的度数为( )
A. B. C. D.
10.(2023·宜宾模拟)如图,在中,,点D、E分别是的中点.将绕点A顺时针旋转,射线与射线交于点P,在这个旋转过程中有下列结论:
①;②存在最大值为;③存在最小值为;④点P运动的路径长为.其中,正确的是( )
A.①③④ B.①②④ C.①②③ D.②③④
二、填空题
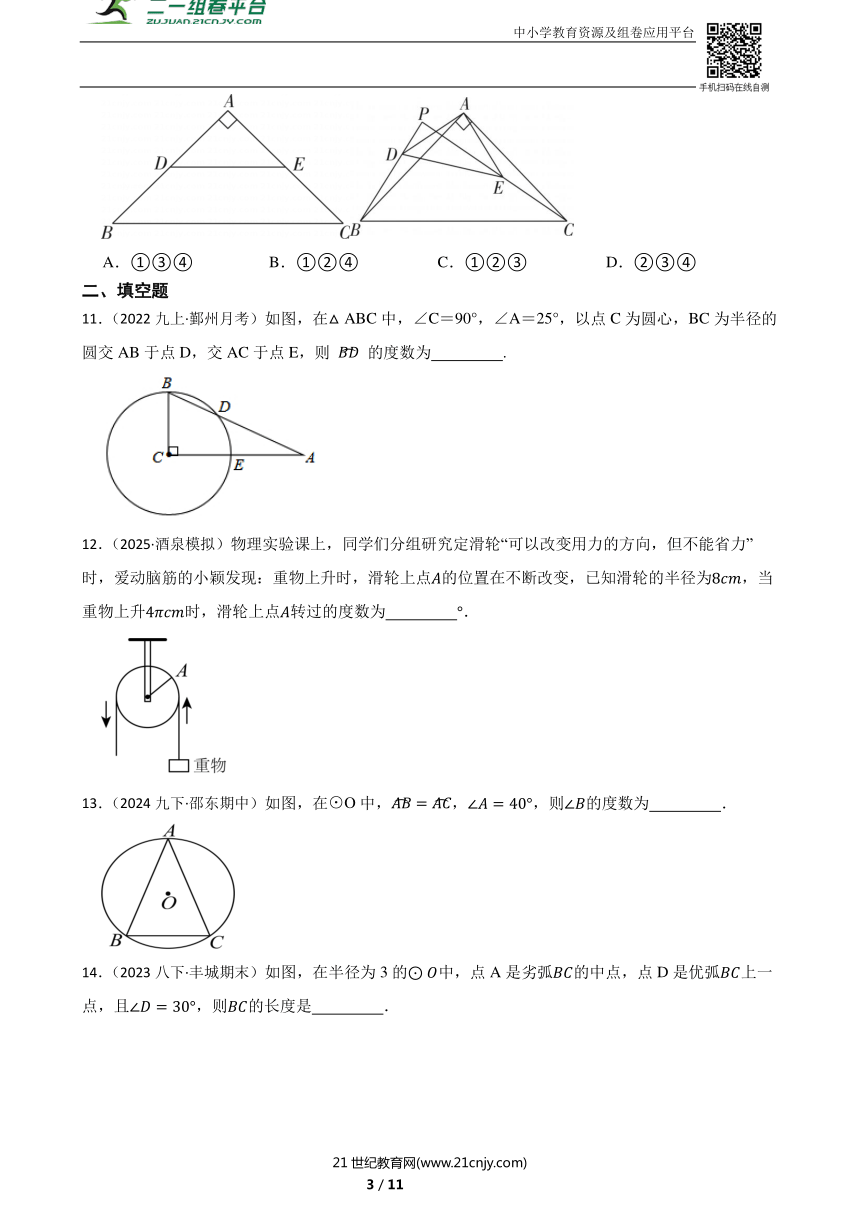
11.(2022九上·鄞州月考)如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 的度数为 .
12.(2025·酒泉模拟)物理实验课上,同学们分组研究定滑轮“可以改变用力的方向,但不能省力”时,爱动脑筋的小颖发现:重物上升时,滑轮上点的位置在不断改变,已知滑轮的半径为,当重物上升时,滑轮上点转过的度数为 .
13.(2024九下·邵东期中)如图,在⊙O中,,,则的度数为 .
14.(2023八下·丰城期末)如图,在半径为3的中,点A是劣弧的中点,点D是优弧上一点,且,则的长度是 .
15.可以用圆的旋转不变性来理解圆心角定理及圆心角、弧、弦、弦心距这四个量之间的对应关系,要注意的是同一条弦对应 条弧.
16.(2024九上·铁岭期末)如图,边长为4的正方形内接于,点E是上的一个动点(不与A、B重合),点F是上的一点,连接,分别与交于点G、H,且,有下列结论:①;②一定是等腰三角形;③四边形的面积随点E位置的变化而变化;④周长的最小值为.其中正确的是 .(把所有正确结论的序号填上)
三、计算题
17.如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
四、解答题
18.(2021·秦淮模拟)如图, 的弦 相交于点P,且 .求证 .
19.(2023九上·临洮期末)如图,是的直径,,,求的度数.
20.(2025·织金模拟)如图,已知是的直径,弦与弦交于点,且,垂足为点,若.
(1)求的度数;
(2)若,求的值;
(3)在(2)的基础上求的值.
21.(2023·自贡)如图,抛物线与x轴交于,两点,与轴交于点.
(1)求抛物线解析式及,两点坐标;
(2)以,,,为顶点的四边形是平行四边形,求点坐标;
(3)该抛物线对称轴上是否存在点,使得,若存在,求出点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】D
【知识点】圆心角、弧、弦的关系
2.【答案】C
【知识点】圆心角、弧、弦的关系
3.【答案】C
【知识点】圆的相关概念;垂径定理;圆心角、弧、弦的关系
4.【答案】B
【知识点】圆心角、弧、弦的关系
5.【答案】C
【知识点】圆心角、弧、弦的关系
6.【答案】D
【知识点】垂径定理;圆心角、弧、弦的关系;确定圆的条件
7.【答案】D
【知识点】圆心角、弧、弦的关系
8.【答案】C
【知识点】等腰三角形的性质;圆心角、弧、弦的关系
9.【答案】B
【知识点】圆心角、弧、弦的关系
10.【答案】C
【知识点】勾股定理;圆心角、弧、弦的关系;三角形全等的判定-SAS
11.【答案】50°
【知识点】等腰三角形的性质;圆心角、弧、弦的关系;直角三角形的性质
12.【答案】90
【知识点】圆心角、弧、弦的关系
13.【答案】
【知识点】圆心角、弧、弦的关系
14.【答案】
【知识点】圆心角、弧、弦的关系
15.【答案】两
【知识点】圆心角、弧、弦的关系
16.【答案】①②④
【知识点】勾股定理;正方形的性质;圆心角、弧、弦的关系;三角形全等的判定-SAS
17.【答案】解:连接OD,
∵AB=2DE=2OD,
∴OD=DE,
又∵∠E=18°,
∴∠DOE=∠E=18°,
∴∠ODC=36°,
同理∠C=∠ODC=36°
∴∠AOC=∠E+∠OCE=54°.
【知识点】圆心角、弧、弦的关系
18.【答案】证明:连接BD.
∴
即
【知识点】等腰三角形的判定;圆心角、弧、弦的关系
19.【答案】
【知识点】圆心角、弧、弦的关系
20.【答案】(1)解:如图,连接,
,
,.
又,
,
即,
,
,
.
(2)解:,
.
,
.
又,
,
,
.
(3)解:由(2)得,,
.
,,
,
.
,
,
,
.
【知识点】含30°角的直角三角形;勾股定理;垂径定理;圆心角、弧、弦的关系
21.【答案】(1)解:∵抛物线与x轴交于,
∴
解得:,
∴抛物线解析式为,
当时,,
∴,
当时,
解得:,
∴
(2)∵,,,
设,
∵以,,,为顶点的四边形是平行四边形
当为对角线时,
解得:,
∴;
当为对角线时,
解得:
∴
当为对角线时,
解得:
∴
综上所述,以,,,为顶点的四边形是平行四边形,或或
(3)解:如图所示,作交于点,为的中点,连接,
∵
∴是等腰直角三角形,
∴在上,
∵,,
∴,,
∵,
∴在上,
设,则
解得:(舍去)
∴点
设直线的解析式为
∴
解得:.
∴直线的解析式
∵,,
∴抛物线对称轴为直线,
当时,,
∴.
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;勾股定理;平行四边形的性质;圆心角、弧、弦的关系;等腰直角三角形
21世纪教育网(www.21cnjy.com)
2 / 11
3.4圆心角
一、单选题
1.(2020九上·净月期末)如图,在⊙O中, = ,∠A=40°,则∠B的度数是( )
A.60° B.40° C.50° D.70°
2.(2025九下·织金月考)将一把折扇展开,可抽象看成一个扇形.若该扇形的半径为3,弧长为,则这个扇形的圆心角的度数为( )
A. B. C. D.
3.(2023九上·肇源期中)下列说法正确的是( )
A.相等的圆心角所对的弧相等,所对的弦相等
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.等弧所对的圆心角相等,所对的弦相等
D.圆是轴对称图形,其对称轴是任意一条直径
4.(2024九上·许昌月考)如图,AB是⊙O的直径,C、D是⊙O上的两点,且点C为弧BAD的中点,连接CD、CB、OD,CD与AB交于点F.若∠AOD=100°,则∠ABC的度数为( )
A.15° B.20° C.25° D.30°
5.(2024九上·南京月考)一个扇形的半径为4,弧长为,其圆心角度数是( )
A. B. C. D.
6.(2018九上·宁波期中)下列四个命题中,正确的有( )
①三点确定一个圆 ②平分弦的直径平分弦所对的弧
③弦长相等,则弦所对的弦心距也相等 ④相等的弧所对的圆心角相等
A.4个 B.3个 C.2个 D.1个
7.(2020九上·建水期末)如图,在⊙O中, ,∠AOD=150°,∠BOC=80°,则∠AOB的度数是( )
A.20° B.25° C.30° D.35°
8.(2024·旺苍模拟)如图,是的两条直径,是劣弧的中点,若,则的度数是( )
A. B. C. D.
9.(2024九上·长春期中)如图,在中,是直径,,,则的度数为( )
A. B. C. D.
10.(2023·宜宾模拟)如图,在中,,点D、E分别是的中点.将绕点A顺时针旋转,射线与射线交于点P,在这个旋转过程中有下列结论:
①;②存在最大值为;③存在最小值为;④点P运动的路径长为.其中,正确的是( )
A.①③④ B.①②④ C.①②③ D.②③④
二、填空题
11.(2022九上·鄞州月考)如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 的度数为 .
12.(2025·酒泉模拟)物理实验课上,同学们分组研究定滑轮“可以改变用力的方向,但不能省力”时,爱动脑筋的小颖发现:重物上升时,滑轮上点的位置在不断改变,已知滑轮的半径为,当重物上升时,滑轮上点转过的度数为 .
13.(2024九下·邵东期中)如图,在⊙O中,,,则的度数为 .
14.(2023八下·丰城期末)如图,在半径为3的中,点A是劣弧的中点,点D是优弧上一点,且,则的长度是 .
15.可以用圆的旋转不变性来理解圆心角定理及圆心角、弧、弦、弦心距这四个量之间的对应关系,要注意的是同一条弦对应 条弧.
16.(2024九上·铁岭期末)如图,边长为4的正方形内接于,点E是上的一个动点(不与A、B重合),点F是上的一点,连接,分别与交于点G、H,且,有下列结论:①;②一定是等腰三角形;③四边形的面积随点E位置的变化而变化;④周长的最小值为.其中正确的是 .(把所有正确结论的序号填上)
三、计算题
17.如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
四、解答题
18.(2021·秦淮模拟)如图, 的弦 相交于点P,且 .求证 .
19.(2023九上·临洮期末)如图,是的直径,,,求的度数.
20.(2025·织金模拟)如图,已知是的直径,弦与弦交于点,且,垂足为点,若.
(1)求的度数;
(2)若,求的值;
(3)在(2)的基础上求的值.
21.(2023·自贡)如图,抛物线与x轴交于,两点,与轴交于点.
(1)求抛物线解析式及,两点坐标;
(2)以,,,为顶点的四边形是平行四边形,求点坐标;
(3)该抛物线对称轴上是否存在点,使得,若存在,求出点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】D
【知识点】圆心角、弧、弦的关系
2.【答案】C
【知识点】圆心角、弧、弦的关系
3.【答案】C
【知识点】圆的相关概念;垂径定理;圆心角、弧、弦的关系
4.【答案】B
【知识点】圆心角、弧、弦的关系
5.【答案】C
【知识点】圆心角、弧、弦的关系
6.【答案】D
【知识点】垂径定理;圆心角、弧、弦的关系;确定圆的条件
7.【答案】D
【知识点】圆心角、弧、弦的关系
8.【答案】C
【知识点】等腰三角形的性质;圆心角、弧、弦的关系
9.【答案】B
【知识点】圆心角、弧、弦的关系
10.【答案】C
【知识点】勾股定理;圆心角、弧、弦的关系;三角形全等的判定-SAS
11.【答案】50°
【知识点】等腰三角形的性质;圆心角、弧、弦的关系;直角三角形的性质
12.【答案】90
【知识点】圆心角、弧、弦的关系
13.【答案】
【知识点】圆心角、弧、弦的关系
14.【答案】
【知识点】圆心角、弧、弦的关系
15.【答案】两
【知识点】圆心角、弧、弦的关系
16.【答案】①②④
【知识点】勾股定理;正方形的性质;圆心角、弧、弦的关系;三角形全等的判定-SAS
17.【答案】解:连接OD,
∵AB=2DE=2OD,
∴OD=DE,
又∵∠E=18°,
∴∠DOE=∠E=18°,
∴∠ODC=36°,
同理∠C=∠ODC=36°
∴∠AOC=∠E+∠OCE=54°.
【知识点】圆心角、弧、弦的关系
18.【答案】证明:连接BD.
∴
即
【知识点】等腰三角形的判定;圆心角、弧、弦的关系
19.【答案】
【知识点】圆心角、弧、弦的关系
20.【答案】(1)解:如图,连接,
,
,.
又,
,
即,
,
,
.
(2)解:,
.
,
.
又,
,
,
.
(3)解:由(2)得,,
.
,,
,
.
,
,
,
.
【知识点】含30°角的直角三角形;勾股定理;垂径定理;圆心角、弧、弦的关系
21.【答案】(1)解:∵抛物线与x轴交于,
∴
解得:,
∴抛物线解析式为,
当时,,
∴,
当时,
解得:,
∴
(2)∵,,,
设,
∵以,,,为顶点的四边形是平行四边形
当为对角线时,
解得:,
∴;
当为对角线时,
解得:
∴
当为对角线时,
解得:
∴
综上所述,以,,,为顶点的四边形是平行四边形,或或
(3)解:如图所示,作交于点,为的中点,连接,
∵
∴是等腰直角三角形,
∴在上,
∵,,
∴,,
∵,
∴在上,
设,则
解得:(舍去)
∴点
设直线的解析式为
∴
解得:.
∴直线的解析式
∵,,
∴抛物线对称轴为直线,
当时,,
∴.
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;勾股定理;平行四边形的性质;圆心角、弧、弦的关系;等腰直角三角形
21世纪教育网(www.21cnjy.com)
2 / 11
同课章节目录
