3.5 圆周角 同步练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
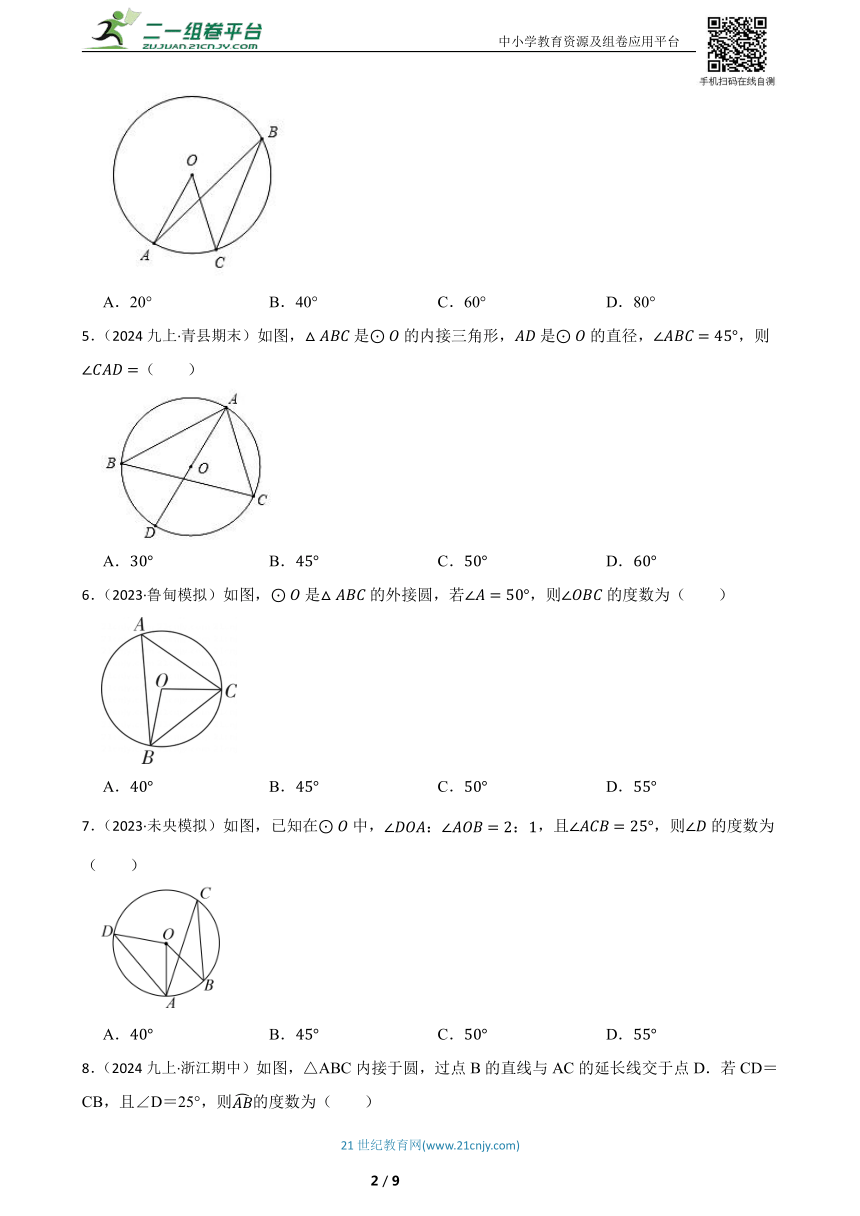
3.5 圆周角
一、单选题
1.(2025·黄石模拟)如图,四边形内接于,,为对角线,经过圆心O.若,则的度数为( )
A. B. C. D.
2.(2024九下·临淄模拟)如图,四边形是的内接四边形,点为弧的中点,,,则的度数为( )
A. B. C. D.
3.(2024九上·沾益月考)如图所示,点D是弦的中点,点C在上,经过圆心O,则下列结论中不一定正确的是( )
A. B.
C. D.弧弧
4.(2023九上·福清期中)如图,点A、B、C在上,,则的度数为( )
A.20° B.40° C.60° D.80°
5.(2024九上·青县期末)如图,是的内接三角形,是的直径,,则( )
A. B. C. D.
6.(2023·鲁甸模拟)如图,是的外接圆,若,则的度数为( )
A. B. C. D.
7.(2023·未央模拟)如图,已知在中,,且,则的度数为( )
A. B. C. D.
8.(2024九上·浙江期中)如图,△ABC内接于圆,过点B的直线与AC的延长线交于点D.若CD=CB,且∠D=25°,则的度数为( )
A.25° B.50° C.75° D.100°
9.(2024九上·三河期末)如图,是⊙的直径,是弦,,交于点,交于点,若,,则⊙的半径是( )
A.5 B.4 C.3 D.23
10.(2022七下·深圳期末)在矩形ABCD中,AB=10,AD=6,点N是线段BC的中点,点E、G分别为射线DA,线段AB上的动点,CE交以DE为直径的圆于点M,则GM+GN的最小值为( ).
A. B. C.5 D.6
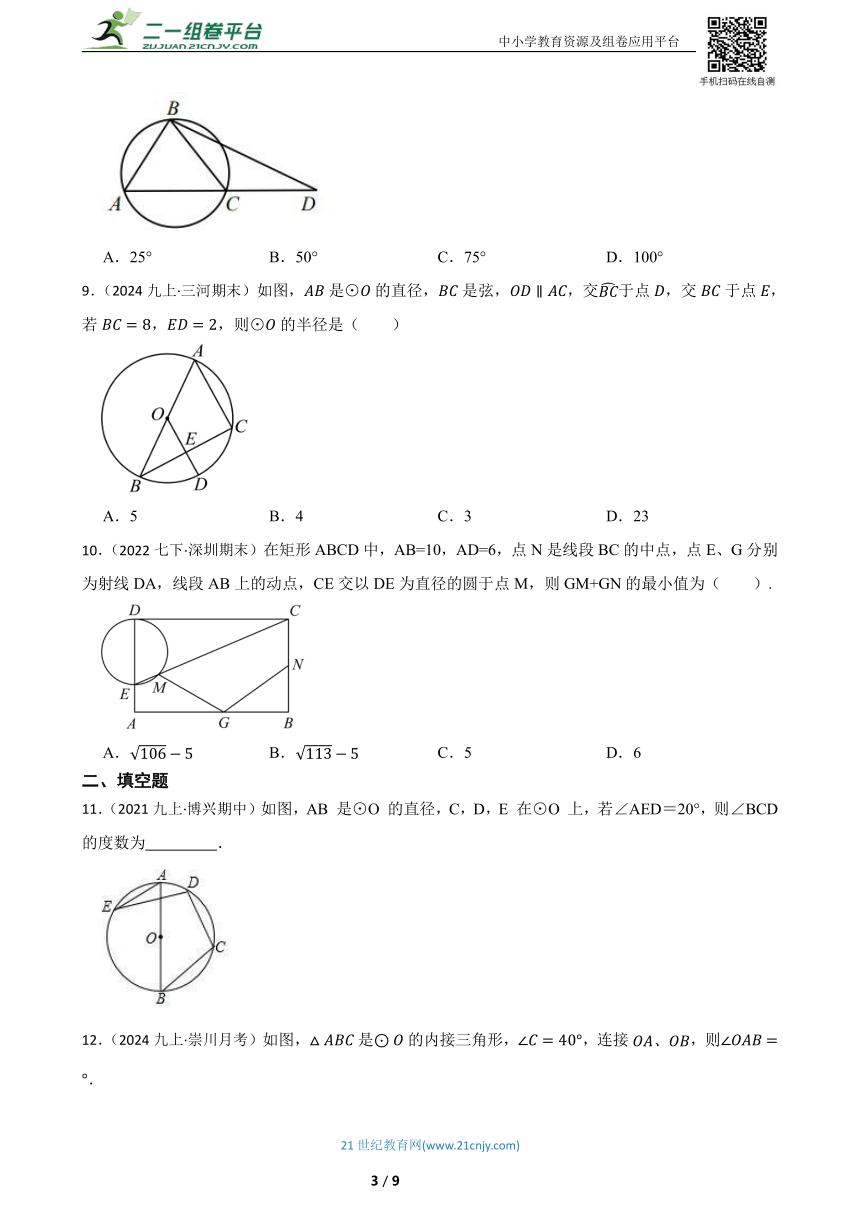
二、填空题
11.(2021九上·博兴期中)如图,AB 是⊙O 的直径,C,D,E 在⊙O 上,若∠AED=20°,则∠BCD 的度数为 .
12.(2024九上·崇川月考)如图,是的内接三角形,,连接,则 .
13.(2019九上·博罗期中)如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠AOB=120°,则∠ACB= °.
14.(2020九上·林口期末)如图,⊙O是△ABC的外接圆,∠A=60°,BC=6 ,则⊙O的半径是 .
15.(2020九上·蓬莱期末)如图,在 中, ,过点A,C的圆的圆心在边 上,点M是优弧 (不与点A,C重合)上的一点,则 .
16.(2024·广州模拟)如图,正方形内接于,线段在对角线上运动,若的面积为,,则(1)的直径长为 ;(2)周长的最小值是 .
三、计算题
17.(2016九上·海淀期中)如图,A,D是半圆上的两点,O为圆心,BC是直径,∠D=35°,求∠OAC的度数.
四、解答题
18.(2024九上·沛县期中)如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D点.求线段BC和AD的长度.
19.(2023九上·久治期末)如图,⊙O中,OA⊥BC,∠AOB=50°,求∠ADC的度数.
20.(2021·太原模拟)如图,⊙O是△ABC的外接圆,∠AOB=96°,∠CAB=60°,点D是 的中点.求∠ABD的度数.
21.(2024九上·张店月考)如图,已知点A、B、C为上互不重合的三点,,图形G关于轴对称后的图形称为,把再关于AC轴对称后的图形称为图形,若图形和都在上或内,则称图形G为关于的“轴转图形”.例如图中点D为关于的“轴转图形”:
如图1,在平面直角坐标系中,的半径为1,上有三点,,
(1)①直接写出的度数;
②在点和点中,点_________为关于的“轴转图形”,且的坐标为_________;
(2)平面内有一条线段EF,且EF是关于的“轴转图形”.
①若EF上所有的点都在上或内,则EF长度的最大值为_________;
②若EF是平面内的任意一条线段,则EF长度的最大值为_________.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】B
【知识点】三角形内角和定理;圆周角定理
3.【答案】B
【知识点】垂径定理的实际应用;圆周角定理
4.【答案】D
【知识点】圆周角定理
5.【答案】B
【知识点】圆周角定理
6.【答案】A
【知识点】等腰三角形的性质;圆周角定理
7.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
8.【答案】D
【知识点】三角形的外角性质;圆周角定理;等腰三角形的性质-等边对等角
9.【答案】A
【知识点】勾股定理;垂径定理;圆周角定理
10.【答案】A
【知识点】勾股定理;矩形的判定与性质;圆周角定理;轴对称的性质
11.【答案】110°
【知识点】圆周角定理
12.【答案】50
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
13.【答案】60
【知识点】圆周角定理
14.【答案】6
【知识点】含30°角的直角三角形;圆周角定理
15.【答案】60
【知识点】圆周角定理
16.【答案】;4
【知识点】勾股定理;平行四边形的判定与性质;正方形的性质;圆周角定理
17.【答案】解法一:
解:∵∠D=35°,
∴∠B=∠D=35°,
∵BC是直径,
∴∠BAC=90°.
∴∠ACB=90°﹣∠ABC=55°,
∵OA=OC,
∴∠OAC=∠OCA=55°.
解法二:
解:∵∠D=35°,
∴∠AOC=2∠D=70°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OCA+∠AOC=180°,
∴∠OAC=55°.
【知识点】圆周角定理
18.【答案】BC=8cm,AD=cm
【知识点】勾股定理;垂径定理;圆周角定理
19.【答案】∠ADC=25°
【知识点】垂径定理;圆周角定理
20.【答案】解:∠AOB=96°,
∴∠ACB=48°,
∵∠CAB=60°,
∴∠ABC=180°-∠ACB-∠CAB=72°, ,
又∵点D是 的中点,
∴ ,
∴∠CBD=30°,
∴∠ABD=∠ABC+∠CBD=102°.
【知识点】圆心角、弧、弦的关系;圆周角定理
21.【答案】(1)①;②D,
(2)①;②
【知识点】勾股定理;圆周角定理;轴对称的性质;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 9
3.5 圆周角
一、单选题
1.(2025·黄石模拟)如图,四边形内接于,,为对角线,经过圆心O.若,则的度数为( )
A. B. C. D.
2.(2024九下·临淄模拟)如图,四边形是的内接四边形,点为弧的中点,,,则的度数为( )
A. B. C. D.
3.(2024九上·沾益月考)如图所示,点D是弦的中点,点C在上,经过圆心O,则下列结论中不一定正确的是( )
A. B.
C. D.弧弧
4.(2023九上·福清期中)如图,点A、B、C在上,,则的度数为( )
A.20° B.40° C.60° D.80°
5.(2024九上·青县期末)如图,是的内接三角形,是的直径,,则( )
A. B. C. D.
6.(2023·鲁甸模拟)如图,是的外接圆,若,则的度数为( )
A. B. C. D.
7.(2023·未央模拟)如图,已知在中,,且,则的度数为( )
A. B. C. D.
8.(2024九上·浙江期中)如图,△ABC内接于圆,过点B的直线与AC的延长线交于点D.若CD=CB,且∠D=25°,则的度数为( )
A.25° B.50° C.75° D.100°
9.(2024九上·三河期末)如图,是⊙的直径,是弦,,交于点,交于点,若,,则⊙的半径是( )
A.5 B.4 C.3 D.23
10.(2022七下·深圳期末)在矩形ABCD中,AB=10,AD=6,点N是线段BC的中点,点E、G分别为射线DA,线段AB上的动点,CE交以DE为直径的圆于点M,则GM+GN的最小值为( ).
A. B. C.5 D.6
二、填空题
11.(2021九上·博兴期中)如图,AB 是⊙O 的直径,C,D,E 在⊙O 上,若∠AED=20°,则∠BCD 的度数为 .
12.(2024九上·崇川月考)如图,是的内接三角形,,连接,则 .
13.(2019九上·博罗期中)如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠AOB=120°,则∠ACB= °.
14.(2020九上·林口期末)如图,⊙O是△ABC的外接圆,∠A=60°,BC=6 ,则⊙O的半径是 .
15.(2020九上·蓬莱期末)如图,在 中, ,过点A,C的圆的圆心在边 上,点M是优弧 (不与点A,C重合)上的一点,则 .
16.(2024·广州模拟)如图,正方形内接于,线段在对角线上运动,若的面积为,,则(1)的直径长为 ;(2)周长的最小值是 .
三、计算题
17.(2016九上·海淀期中)如图,A,D是半圆上的两点,O为圆心,BC是直径,∠D=35°,求∠OAC的度数.
四、解答题
18.(2024九上·沛县期中)如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D点.求线段BC和AD的长度.
19.(2023九上·久治期末)如图,⊙O中,OA⊥BC,∠AOB=50°,求∠ADC的度数.
20.(2021·太原模拟)如图,⊙O是△ABC的外接圆,∠AOB=96°,∠CAB=60°,点D是 的中点.求∠ABD的度数.
21.(2024九上·张店月考)如图,已知点A、B、C为上互不重合的三点,,图形G关于轴对称后的图形称为,把再关于AC轴对称后的图形称为图形,若图形和都在上或内,则称图形G为关于的“轴转图形”.例如图中点D为关于的“轴转图形”:
如图1,在平面直角坐标系中,的半径为1,上有三点,,
(1)①直接写出的度数;
②在点和点中,点_________为关于的“轴转图形”,且的坐标为_________;
(2)平面内有一条线段EF,且EF是关于的“轴转图形”.
①若EF上所有的点都在上或内,则EF长度的最大值为_________;
②若EF是平面内的任意一条线段,则EF长度的最大值为_________.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】B
【知识点】三角形内角和定理;圆周角定理
3.【答案】B
【知识点】垂径定理的实际应用;圆周角定理
4.【答案】D
【知识点】圆周角定理
5.【答案】B
【知识点】圆周角定理
6.【答案】A
【知识点】等腰三角形的性质;圆周角定理
7.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
8.【答案】D
【知识点】三角形的外角性质;圆周角定理;等腰三角形的性质-等边对等角
9.【答案】A
【知识点】勾股定理;垂径定理;圆周角定理
10.【答案】A
【知识点】勾股定理;矩形的判定与性质;圆周角定理;轴对称的性质
11.【答案】110°
【知识点】圆周角定理
12.【答案】50
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
13.【答案】60
【知识点】圆周角定理
14.【答案】6
【知识点】含30°角的直角三角形;圆周角定理
15.【答案】60
【知识点】圆周角定理
16.【答案】;4
【知识点】勾股定理;平行四边形的判定与性质;正方形的性质;圆周角定理
17.【答案】解法一:
解:∵∠D=35°,
∴∠B=∠D=35°,
∵BC是直径,
∴∠BAC=90°.
∴∠ACB=90°﹣∠ABC=55°,
∵OA=OC,
∴∠OAC=∠OCA=55°.
解法二:
解:∵∠D=35°,
∴∠AOC=2∠D=70°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OCA+∠AOC=180°,
∴∠OAC=55°.
【知识点】圆周角定理
18.【答案】BC=8cm,AD=cm
【知识点】勾股定理;垂径定理;圆周角定理
19.【答案】∠ADC=25°
【知识点】垂径定理;圆周角定理
20.【答案】解:∠AOB=96°,
∴∠ACB=48°,
∵∠CAB=60°,
∴∠ABC=180°-∠ACB-∠CAB=72°, ,
又∵点D是 的中点,
∴ ,
∴∠CBD=30°,
∴∠ABD=∠ABC+∠CBD=102°.
【知识点】圆心角、弧、弦的关系;圆周角定理
21.【答案】(1)①;②D,
(2)①;②
【知识点】勾股定理;圆周角定理;轴对称的性质;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
