4.4 两个三角形相似的判定 同步练习(含答案)
文档属性
| 名称 | 4.4 两个三角形相似的判定 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 512.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:26:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.4 两个三角形相似的判定
一、单选题
1.(2023九上·义乌月考)如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B.∠DAC=∠ABC
C.AC2=BC CD D.
2.(2025九下·杭州月考)如图,四个三角形的顶点都在方格子的格点上,下列两个三角形中相似的是( )
A.①④ B.①③ C.②③ D.②④
3.(2019九上·崇明期末)如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE 的是( )
A.∠B=∠D B.∠C=∠AED
C. = D. =
4.(2024九上·鹿邑期末)下列两个图形,一定相似的是( )
A.两个等腰三角形 B.两个直角三角形
C.两个等边三角形 D.两个矩形
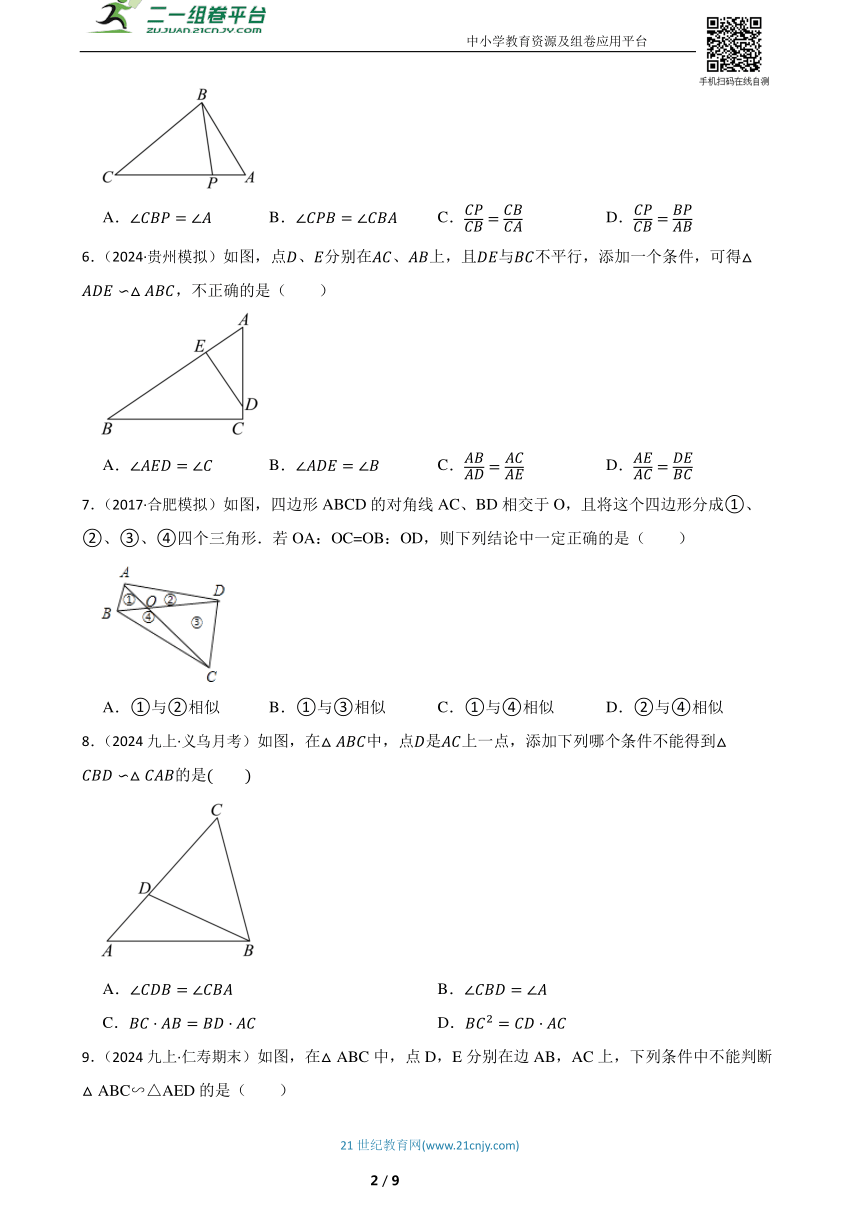
5.(2024九上·商水期末)如图,点P在的边上,要判断,需添加一个条件,其中不正确的是( )
A. B. C. D.
6.(2024·贵州模拟)如图,点、分别在、上,且与不平行,添加一个条件,可得,不正确的是( )
A. B. C. D.
7.(2017·合肥模拟)如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似 C.①与④相似 D.②与④相似
8.(2024九上·义乌月考)如图,在中,点是上一点,添加下列哪个条件不能得到的是
A. B.
C. D.
9.(2024九上·仁寿期末)如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
10.如图,在中,为线段AB上两动点,且,过点E,~F分别作BC,~AC的垂线相交于点,垂足分别为,.现有以下结论:①;②当点与点重合时,;③;④,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.(2023九下·恩施月考)如图,点是中边上的一点,请你添加一个条件使,这个条件可以是 .
12.(2023九上·海陵月考)如图,正方形的边长为8,,,线段的两端在、上滑动,当 时,与相似.
13.(2023九上·东乡区期中)如图,在中,、分别为、边上的点,,若,,,则 .
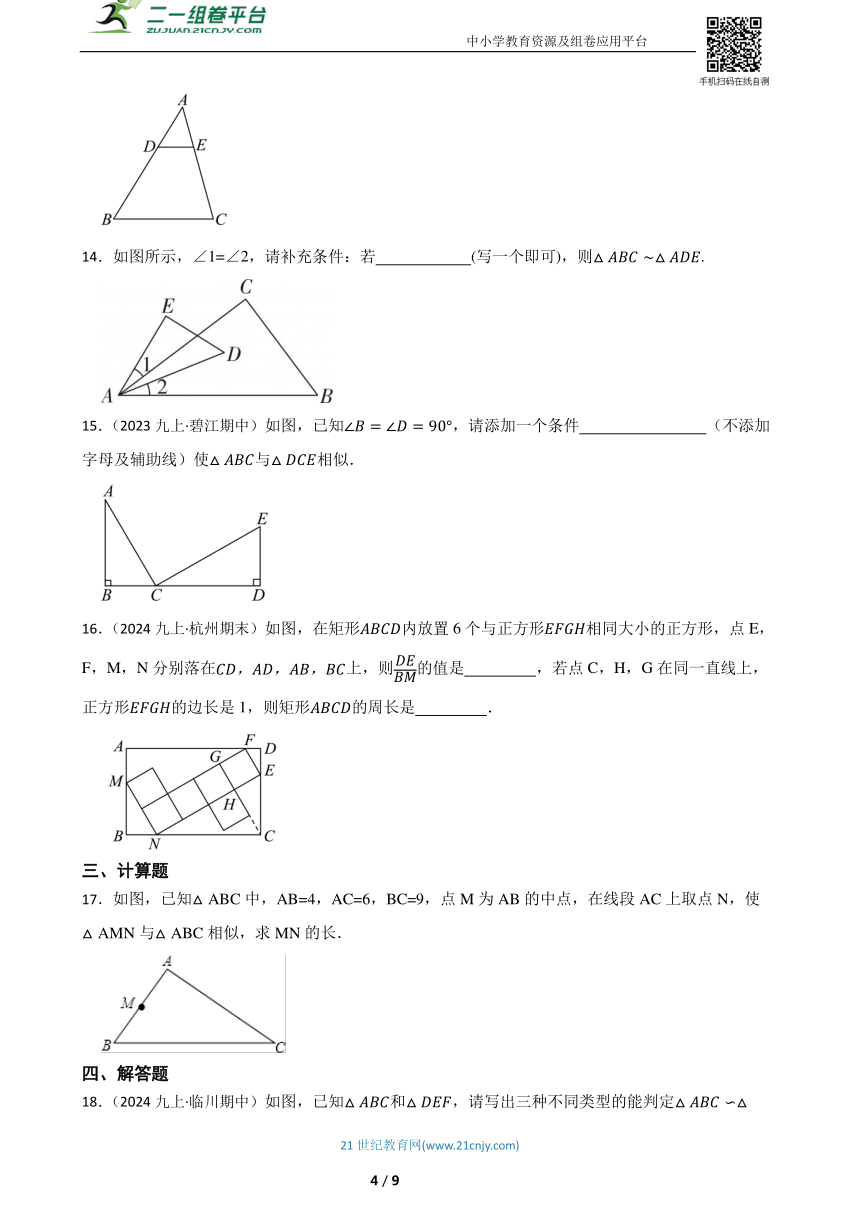
14.如图所示,∠1=∠2,请补充条件:若 (写一个即可),则.
15.(2023九上·碧江期中)如图,已知,请添加一个条件 (不添加字母及辅助线)使与相似.
16.(2024九上·杭州期末)如图,在矩形内放置6个与正方形相同大小的正方形,点E,F,M,N分别落在上,则的值是 ,若点C,H,G在同一直线上,正方形的边长是1,则矩形的周长是 .
三、计算题
17.如图,已知△ABC中,AB=4,AC=6,BC=9,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
四、解答题
18.(2024九上·临川期中)如图,已知和,请写出三种不同类型的能判定的条件.
(1)_________________(2)_________________(3)_________________
19.(2024九上·杭州期末)如图,在中,是边上的点,已知.
(1)求证:;
(2)若,,求的值.
20.如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,证明:△ABC∽△CDE.
21.(2024·重庆)如图1,在中,,,点P为AB上一点,,过点P作交AC于点Q点P,Q的距离为,的周长与的周长之比为.
(1)请直接写出,分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中,画出函数,的图象,并分别写出函数,的一条性质;
(3)结合函数图象,请直接写出时x的取值范围(近似值保留小数点后一位,误差不超过0.2).
答案解析部分
1.【答案】C
【知识点】相似三角形的判定
2.【答案】B
【知识点】勾股定理;相似三角形的判定
3.【答案】C
【知识点】相似三角形的判定
4.【答案】C
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】D
【知识点】相似三角形的判定
7.【答案】B
【知识点】相似三角形的判定
8.【答案】C
【知识点】相似三角形的判定
9.【答案】D
【知识点】相似三角形的判定
10.【答案】C
【知识点】三角形全等及其性质;勾股定理;相似三角形的判定;三角形的中位线定理;相似三角形的性质-对应边
11.【答案】(答案不唯一)
【知识点】相似三角形的判定
12.【答案】2或4
【知识点】正方形的性质;相似三角形的判定
13.【答案】
【知识点】相似三角形的性质;相似三角形的判定
14.【答案】
【知识点】相似三角形的判定
15.【答案】
【知识点】相似三角形的判定
16.【答案】;
【知识点】勾股定理;矩形的性质;正方形的性质;相似三角形的判定-AA;相似三角形的性质-对应边
17.【答案】解:∵△ABC中,AB=4,点M为AB的中点,
∴AM=2.
当△AMN∽△ABC时, = ,即 = ,解得MN= ;
当△AMN∽△ACB时, = ,即 = ,解得MN=3.
∴MN的长为: 或3
【知识点】相似三角形的判定
18.【答案】(1);(2),;(3),
【知识点】相似三角形的判定
19.【答案】(1)证明:,,
(2)解:,
,
.
【知识点】相似三角形的判定-AA;相似三角形的性质-对应边
20.【答案】证明:∵∠B=90°, ∴∠A+∠ACB=90°,∵C为线段BD上一点,且AC⊥CE,∴∠ACB+∠ECD=90°,∴∠A=∠ECD,∵∠B=∠D=90°,∴△ABC∽△CDE.
【知识点】相似三角形的判定
21.【答案】(1)解:∵,
,
,
,,
∴,;
(2)解:如图所示,即为所求;
由函数图象可知,随x增大而增大,随x增大而减小;
(3)解:由函数图象可知,当时x的取值范围.
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;相似三角形的性质;相似三角形的判定
21世纪教育网(www.21cnjy.com)
5 / 9
4.4 两个三角形相似的判定
一、单选题
1.(2023九上·义乌月考)如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B.∠DAC=∠ABC
C.AC2=BC CD D.
2.(2025九下·杭州月考)如图,四个三角形的顶点都在方格子的格点上,下列两个三角形中相似的是( )
A.①④ B.①③ C.②③ D.②④
3.(2019九上·崇明期末)如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE 的是( )
A.∠B=∠D B.∠C=∠AED
C. = D. =
4.(2024九上·鹿邑期末)下列两个图形,一定相似的是( )
A.两个等腰三角形 B.两个直角三角形
C.两个等边三角形 D.两个矩形
5.(2024九上·商水期末)如图,点P在的边上,要判断,需添加一个条件,其中不正确的是( )
A. B. C. D.
6.(2024·贵州模拟)如图,点、分别在、上,且与不平行,添加一个条件,可得,不正确的是( )
A. B. C. D.
7.(2017·合肥模拟)如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似 C.①与④相似 D.②与④相似
8.(2024九上·义乌月考)如图,在中,点是上一点,添加下列哪个条件不能得到的是
A. B.
C. D.
9.(2024九上·仁寿期末)如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
10.如图,在中,为线段AB上两动点,且,过点E,~F分别作BC,~AC的垂线相交于点,垂足分别为,.现有以下结论:①;②当点与点重合时,;③;④,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.(2023九下·恩施月考)如图,点是中边上的一点,请你添加一个条件使,这个条件可以是 .
12.(2023九上·海陵月考)如图,正方形的边长为8,,,线段的两端在、上滑动,当 时,与相似.
13.(2023九上·东乡区期中)如图,在中,、分别为、边上的点,,若,,,则 .
14.如图所示,∠1=∠2,请补充条件:若 (写一个即可),则.
15.(2023九上·碧江期中)如图,已知,请添加一个条件 (不添加字母及辅助线)使与相似.
16.(2024九上·杭州期末)如图,在矩形内放置6个与正方形相同大小的正方形,点E,F,M,N分别落在上,则的值是 ,若点C,H,G在同一直线上,正方形的边长是1,则矩形的周长是 .
三、计算题
17.如图,已知△ABC中,AB=4,AC=6,BC=9,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
四、解答题
18.(2024九上·临川期中)如图,已知和,请写出三种不同类型的能判定的条件.
(1)_________________(2)_________________(3)_________________
19.(2024九上·杭州期末)如图,在中,是边上的点,已知.
(1)求证:;
(2)若,,求的值.
20.如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,证明:△ABC∽△CDE.
21.(2024·重庆)如图1,在中,,,点P为AB上一点,,过点P作交AC于点Q点P,Q的距离为,的周长与的周长之比为.
(1)请直接写出,分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中,画出函数,的图象,并分别写出函数,的一条性质;
(3)结合函数图象,请直接写出时x的取值范围(近似值保留小数点后一位,误差不超过0.2).
答案解析部分
1.【答案】C
【知识点】相似三角形的判定
2.【答案】B
【知识点】勾股定理;相似三角形的判定
3.【答案】C
【知识点】相似三角形的判定
4.【答案】C
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】D
【知识点】相似三角形的判定
7.【答案】B
【知识点】相似三角形的判定
8.【答案】C
【知识点】相似三角形的判定
9.【答案】D
【知识点】相似三角形的判定
10.【答案】C
【知识点】三角形全等及其性质;勾股定理;相似三角形的判定;三角形的中位线定理;相似三角形的性质-对应边
11.【答案】(答案不唯一)
【知识点】相似三角形的判定
12.【答案】2或4
【知识点】正方形的性质;相似三角形的判定
13.【答案】
【知识点】相似三角形的性质;相似三角形的判定
14.【答案】
【知识点】相似三角形的判定
15.【答案】
【知识点】相似三角形的判定
16.【答案】;
【知识点】勾股定理;矩形的性质;正方形的性质;相似三角形的判定-AA;相似三角形的性质-对应边
17.【答案】解:∵△ABC中,AB=4,点M为AB的中点,
∴AM=2.
当△AMN∽△ABC时, = ,即 = ,解得MN= ;
当△AMN∽△ACB时, = ,即 = ,解得MN=3.
∴MN的长为: 或3
【知识点】相似三角形的判定
18.【答案】(1);(2),;(3),
【知识点】相似三角形的判定
19.【答案】(1)证明:,,
(2)解:,
,
.
【知识点】相似三角形的判定-AA;相似三角形的性质-对应边
20.【答案】证明:∵∠B=90°, ∴∠A+∠ACB=90°,∵C为线段BD上一点,且AC⊥CE,∴∠ACB+∠ECD=90°,∴∠A=∠ECD,∵∠B=∠D=90°,∴△ABC∽△CDE.
【知识点】相似三角形的判定
21.【答案】(1)解:∵,
,
,
,,
∴,;
(2)解:如图所示,即为所求;
由函数图象可知,随x增大而增大,随x增大而减小;
(3)解:由函数图象可知,当时x的取值范围.
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;相似三角形的性质;相似三角形的判定
21世纪教育网(www.21cnjy.com)
5 / 9
同课章节目录
