4.5 相似三角形的性质及应用 同步练习(含答案)
文档属性
| 名称 | 4.5 相似三角形的性质及应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 389.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:25:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.5 相似三角形的性质及应用
一、单选题
1.(2022九上·西安月考)两个相似三角形对应中线的长分别为6cm和12cm,若较大三角形的面积是12cm2,则较小的三角形的面积为( )cm2.
A.1 B.3 C.4 D.6
2.(2025·龙马潭模拟)如图,,若,,则与的相似比是( )
A. B. C. D.
3.(2024九下·泰州月考)如图,已知等边的面积为1,D、E分别为的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是( )
A. B. C. D.
4.(2023九上·平南期中)如图,在中,点分别在上,平分交于点,若,则的值为( )
A. B. C. D.
5.(2019九上·定边期中)已知△ABC∽△A B C ,且△ABC与△A B C 的周长比为 ,则△ABC与△A B C 的面积比为( )
A. B. C. D.
6.已知两个相似三角形周长分别为8和6,则它们的面积比为( )。
A.4:3 B.16:9 C. D.
7.(2019九上·乐亭期中)如图,在 ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A. B. C. D.
8.若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
A.1:4 B.2:1 C.1:2 D.4:1
9.已知小丽同学身高1.5米,经太阳光照射,在地面的影长为2米,她此时测得一建筑物在同一地面的影长为40米,那么这个建筑物的高为( )
A.20米 B.30米 C.40米 D.50米
10.(2018九上·港南期中)如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为( )
①OH= BF;②∠CHF=45°;③GH= BC;④DH2=HE HB.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2023九上·秦皇岛期末)在阳光下的某一时刻,测得教学楼在地面上的影子长为 ,此时 高的标杆竖立在地面上的影子长为 ,则教学楼的高度为 .
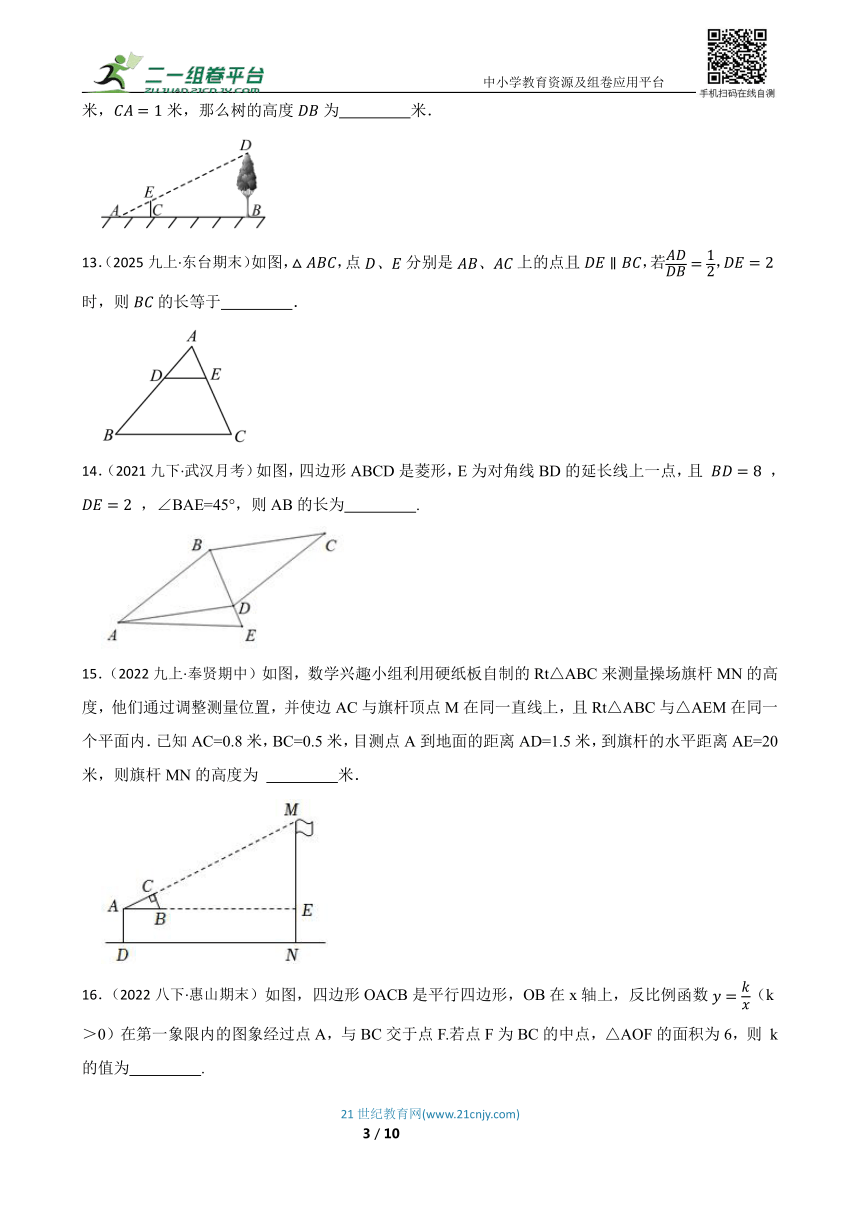
12.(2023九上·柳州月考)如图,某学生利用一根长0.5米的标杆测量一棵树的高度,测得米,米,那么树的高度为 米.
13.(2025九上·东台期末)如图,,点分别是上的点且,若,时,则的长等于 .
14.(2021九下·武汉月考)如图,四边形ABCD是菱形,E为对角线BD的延长线上一点,且 , ,∠BAE=45°,则AB的长为 .
15.(2022九上·奉贤期中)如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米.
16.(2022八下·惠山期末)如图,四边形OACB是平行四边形,OB在x轴上,反比例函数(k>0)在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,△AOF的面积为6,则 k的值为 .
三、计算题
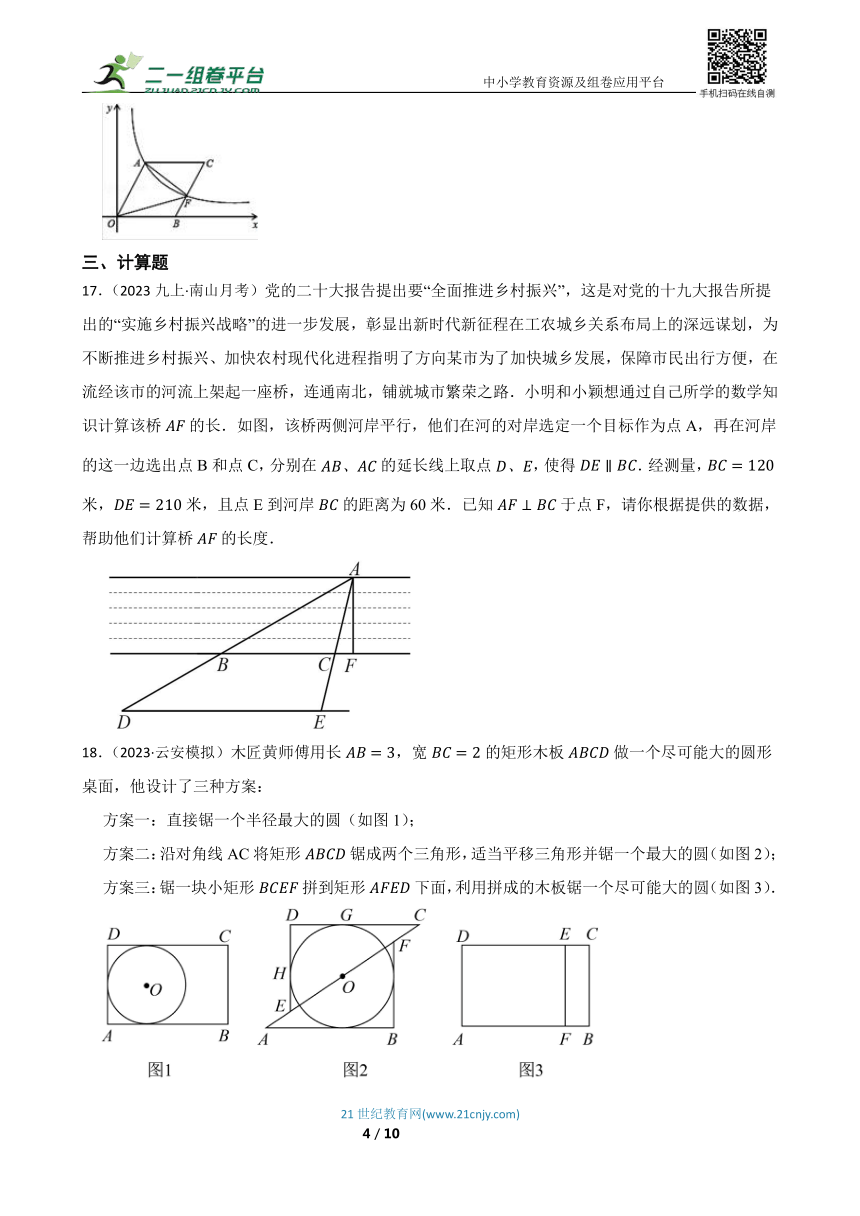
17.(2023九上·南山月考)党的二十大报告提出要“全面推进乡村振兴”,这是对党的十九大报告所提出的“实施乡村振兴战略”的进一步发展,彰显出新时代新征程在工农城乡关系布局上的深远谋划,为不断推进乡村振兴、加快农村现代化进程指明了方向某市为了加快城乡发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量,米,米,且点E到河岸的距离为60米.已知于点F,请你根据提供的数据,帮助他们计算桥的长度.
18.(2023·云安模拟)木匠黄师傅用长,宽的矩形木板做一个尽可能大的圆形桌面,他设计了三种方案:
方案一:直接锯一个半径最大的圆(如图1);
方案二:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆(如图2);
方案三:锯一块小矩形拼到矩形下面,利用拼成的木板锯一个尽可能大的圆(如图3).
(1)通过计算说明方案一和方案二中,哪个圆的半径较大?
(2)在方案三中,设,圆的半径为y.
①求y关于x的函数解析式;
②当x取何值时圆的半径最大,最大半径为多少?并说明三种方案中哪一个圆形桌面的半径最大.
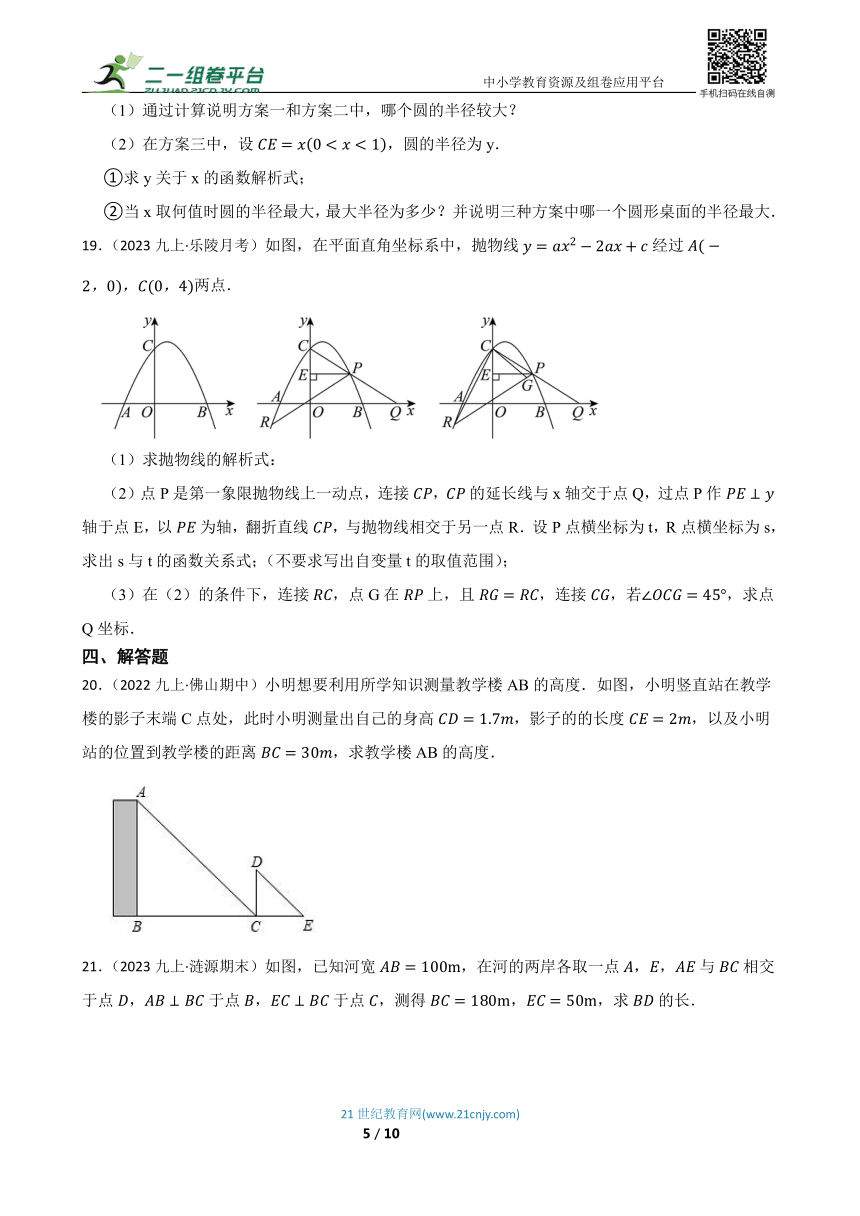
19.(2023九上·乐陵月考)如图,在平面直角坐标系中,抛物线经过两点.
(1)求抛物线的解析式:
(2)点P是第一象限抛物线上一动点,连接,的延长线与x轴交于点Q,过点P作轴于点E,以为轴,翻折直线,与抛物线相交于另一点R.设P点横坐标为t,R点横坐标为s,求出s与t的函数关系式;(不要求写出自变量t的取值范围);
(3)在(2)的条件下,连接,点G在上,且,连接,若,求点Q坐标.
四、解答题
20.(2022九上·佛山期中)小明想要利用所学知识测量教学楼AB的高度.如图,小明竖直站在教学楼的影子末端C点处,此时小明测量出自己的身高,影子的的长度,以及小明站的位置到教学楼的距离,求教学楼AB的高度.
21.(2023九上·涟源期末)如图,已知河宽,在河的两岸各取一点,,与相交于点,于点,于点,测得,,求的长.
22.(2023九上·高州月考)如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
(1)求证:;
(2)求证:;
(3)若,求CG的长.
23.(2024·河南模拟)在平面直角坐标系xOy中,矩形ABCO的顶点A、C分别在y轴、x轴正半轴上,点P在AB上,PA=1,AO=2.经过原点的抛物线的对称轴是直线x=2.
(1)求出该抛物线的解析式.
(2)如图1,将一块两直角边足够长的三角板的直角顶点放在P点处,两直角边恰好分别经过点O和C.现在利用图2进行如下探究:
①将三角板从图1中的位置开始,绕点P顺时针旋转,两直角边分别交OA、OC于点E、F,当点E和点A重合时停止旋转.请你观察、猜想,在这个过程中,的值是否发生变化?若发生变化,说明理由;若不发生变化,求出的值.
②设(1)中的抛物线与x轴的另一个交点为D,顶点为M,在①的旋转过程中,是否存在点F,使△DMF为等腰三角形?若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】相似三角形的性质
2.【答案】B
【知识点】相似三角形的性质
3.【答案】D
【知识点】相似三角形的判定与性质;几何概率;三角形的中位线定理
4.【答案】A
【知识点】相似三角形的判定与性质
5.【答案】C
【知识点】相似三角形的性质
6.【答案】B
【知识点】相似三角形的性质
7.【答案】D
【知识点】相似三角形的判定与性质
8.【答案】C
【知识点】相似三角形的性质
9.【答案】B
【知识点】相似三角形的应用
10.【答案】C
【知识点】全等三角形的判定与性质;正方形的性质;相似三角形的判定与性质;三角形的中位线定理
11.【答案】
【知识点】相似三角形的判定与性质;相似三角形的应用
12.【答案】2
【知识点】相似三角形的应用
13.【答案】6
【知识点】相似三角形的判定与性质
14.【答案】
【知识点】菱形的性质;相似三角形的判定与性质
15.【答案】14
【知识点】相似三角形的应用
16.【答案】8
【知识点】反比例函数系数k的几何意义;直角三角形全等的判定-HL;平行四边形的性质;相似三角形的判定与性质
17.【答案】桥的长度为80米.
【知识点】相似三角形的应用
18.【答案】(1)方案二中圆的半径较大
(2)①当时,;当时,;当时,;②当时,最大为,方案三中圆形桌面的半径最大
【知识点】矩形的性质;相似三角形的判定与性质
19.【答案】(1)
(2)
(3)
【知识点】相似三角形的判定与性质
20.【答案】教学楼AB的高度为.
【知识点】相似三角形的应用
21.【答案】
【知识点】相似三角形的应用
22.【答案】(1)证明:∵BD是正方形ABCD的对角线,
∴,又,
在和中,
,
∴(SAS),
∴;
(2)证明:∵四边形ABCD是正方形,
∴,
∴,
由(1)可知,
∴,
∴,即,
∴,
又,
∴;
(3)解:由(2)得,
∴,即,
∴或(舍去),根据(1)中的结论得,
∴.
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
23.【答案】(1)
(2)①的值不变,;②存在点F(,0)或F(,0),使△DMF为等腰三角形.
【知识点】待定系数法求二次函数解析式;相似三角形的判定与性质;旋转的性质;等腰三角形的概念
21世纪教育网(www.21cnjy.com)
1 / 10
4.5 相似三角形的性质及应用
一、单选题
1.(2022九上·西安月考)两个相似三角形对应中线的长分别为6cm和12cm,若较大三角形的面积是12cm2,则较小的三角形的面积为( )cm2.
A.1 B.3 C.4 D.6
2.(2025·龙马潭模拟)如图,,若,,则与的相似比是( )
A. B. C. D.
3.(2024九下·泰州月考)如图,已知等边的面积为1,D、E分别为的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是( )
A. B. C. D.
4.(2023九上·平南期中)如图,在中,点分别在上,平分交于点,若,则的值为( )
A. B. C. D.
5.(2019九上·定边期中)已知△ABC∽△A B C ,且△ABC与△A B C 的周长比为 ,则△ABC与△A B C 的面积比为( )
A. B. C. D.
6.已知两个相似三角形周长分别为8和6,则它们的面积比为( )。
A.4:3 B.16:9 C. D.
7.(2019九上·乐亭期中)如图,在 ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A. B. C. D.
8.若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
A.1:4 B.2:1 C.1:2 D.4:1
9.已知小丽同学身高1.5米,经太阳光照射,在地面的影长为2米,她此时测得一建筑物在同一地面的影长为40米,那么这个建筑物的高为( )
A.20米 B.30米 C.40米 D.50米
10.(2018九上·港南期中)如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为( )
①OH= BF;②∠CHF=45°;③GH= BC;④DH2=HE HB.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2023九上·秦皇岛期末)在阳光下的某一时刻,测得教学楼在地面上的影子长为 ,此时 高的标杆竖立在地面上的影子长为 ,则教学楼的高度为 .
12.(2023九上·柳州月考)如图,某学生利用一根长0.5米的标杆测量一棵树的高度,测得米,米,那么树的高度为 米.
13.(2025九上·东台期末)如图,,点分别是上的点且,若,时,则的长等于 .
14.(2021九下·武汉月考)如图,四边形ABCD是菱形,E为对角线BD的延长线上一点,且 , ,∠BAE=45°,则AB的长为 .
15.(2022九上·奉贤期中)如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米.
16.(2022八下·惠山期末)如图,四边形OACB是平行四边形,OB在x轴上,反比例函数(k>0)在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,△AOF的面积为6,则 k的值为 .
三、计算题
17.(2023九上·南山月考)党的二十大报告提出要“全面推进乡村振兴”,这是对党的十九大报告所提出的“实施乡村振兴战略”的进一步发展,彰显出新时代新征程在工农城乡关系布局上的深远谋划,为不断推进乡村振兴、加快农村现代化进程指明了方向某市为了加快城乡发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量,米,米,且点E到河岸的距离为60米.已知于点F,请你根据提供的数据,帮助他们计算桥的长度.
18.(2023·云安模拟)木匠黄师傅用长,宽的矩形木板做一个尽可能大的圆形桌面,他设计了三种方案:
方案一:直接锯一个半径最大的圆(如图1);
方案二:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆(如图2);
方案三:锯一块小矩形拼到矩形下面,利用拼成的木板锯一个尽可能大的圆(如图3).
(1)通过计算说明方案一和方案二中,哪个圆的半径较大?
(2)在方案三中,设,圆的半径为y.
①求y关于x的函数解析式;
②当x取何值时圆的半径最大,最大半径为多少?并说明三种方案中哪一个圆形桌面的半径最大.
19.(2023九上·乐陵月考)如图,在平面直角坐标系中,抛物线经过两点.
(1)求抛物线的解析式:
(2)点P是第一象限抛物线上一动点,连接,的延长线与x轴交于点Q,过点P作轴于点E,以为轴,翻折直线,与抛物线相交于另一点R.设P点横坐标为t,R点横坐标为s,求出s与t的函数关系式;(不要求写出自变量t的取值范围);
(3)在(2)的条件下,连接,点G在上,且,连接,若,求点Q坐标.
四、解答题
20.(2022九上·佛山期中)小明想要利用所学知识测量教学楼AB的高度.如图,小明竖直站在教学楼的影子末端C点处,此时小明测量出自己的身高,影子的的长度,以及小明站的位置到教学楼的距离,求教学楼AB的高度.
21.(2023九上·涟源期末)如图,已知河宽,在河的两岸各取一点,,与相交于点,于点,于点,测得,,求的长.
22.(2023九上·高州月考)如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
(1)求证:;
(2)求证:;
(3)若,求CG的长.
23.(2024·河南模拟)在平面直角坐标系xOy中,矩形ABCO的顶点A、C分别在y轴、x轴正半轴上,点P在AB上,PA=1,AO=2.经过原点的抛物线的对称轴是直线x=2.
(1)求出该抛物线的解析式.
(2)如图1,将一块两直角边足够长的三角板的直角顶点放在P点处,两直角边恰好分别经过点O和C.现在利用图2进行如下探究:
①将三角板从图1中的位置开始,绕点P顺时针旋转,两直角边分别交OA、OC于点E、F,当点E和点A重合时停止旋转.请你观察、猜想,在这个过程中,的值是否发生变化?若发生变化,说明理由;若不发生变化,求出的值.
②设(1)中的抛物线与x轴的另一个交点为D,顶点为M,在①的旋转过程中,是否存在点F,使△DMF为等腰三角形?若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】相似三角形的性质
2.【答案】B
【知识点】相似三角形的性质
3.【答案】D
【知识点】相似三角形的判定与性质;几何概率;三角形的中位线定理
4.【答案】A
【知识点】相似三角形的判定与性质
5.【答案】C
【知识点】相似三角形的性质
6.【答案】B
【知识点】相似三角形的性质
7.【答案】D
【知识点】相似三角形的判定与性质
8.【答案】C
【知识点】相似三角形的性质
9.【答案】B
【知识点】相似三角形的应用
10.【答案】C
【知识点】全等三角形的判定与性质;正方形的性质;相似三角形的判定与性质;三角形的中位线定理
11.【答案】
【知识点】相似三角形的判定与性质;相似三角形的应用
12.【答案】2
【知识点】相似三角形的应用
13.【答案】6
【知识点】相似三角形的判定与性质
14.【答案】
【知识点】菱形的性质;相似三角形的判定与性质
15.【答案】14
【知识点】相似三角形的应用
16.【答案】8
【知识点】反比例函数系数k的几何意义;直角三角形全等的判定-HL;平行四边形的性质;相似三角形的判定与性质
17.【答案】桥的长度为80米.
【知识点】相似三角形的应用
18.【答案】(1)方案二中圆的半径较大
(2)①当时,;当时,;当时,;②当时,最大为,方案三中圆形桌面的半径最大
【知识点】矩形的性质;相似三角形的判定与性质
19.【答案】(1)
(2)
(3)
【知识点】相似三角形的判定与性质
20.【答案】教学楼AB的高度为.
【知识点】相似三角形的应用
21.【答案】
【知识点】相似三角形的应用
22.【答案】(1)证明:∵BD是正方形ABCD的对角线,
∴,又,
在和中,
,
∴(SAS),
∴;
(2)证明:∵四边形ABCD是正方形,
∴,
∴,
由(1)可知,
∴,
∴,即,
∴,
又,
∴;
(3)解:由(2)得,
∴,即,
∴或(舍去),根据(1)中的结论得,
∴.
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
23.【答案】(1)
(2)①的值不变,;②存在点F(,0)或F(,0),使△DMF为等腰三角形.
【知识点】待定系数法求二次函数解析式;相似三角形的判定与性质;旋转的性质;等腰三角形的概念
21世纪教育网(www.21cnjy.com)
1 / 10
同课章节目录
